Lonsdaleite vs. Diamond: Strength and Stiffness Analysis

This report, based on first-principles calculations, investigates the mechanical properties of lonsdaleite, a hexagonal form of carbon, and compares them to those of diamond. The study reveals that lonsdaleite exhibits superior compressive strength, Young's modulus, and stiffness compared to diamond. The research explores the material's elastic stiffness, bulk modulus, compressive strength, and tensile strength. The findings suggest that lonsdaleite is a stronger and stiffer naturally occurring substance. The report analyzes stress-strain curves to determine the compressive and tensile strengths along different orientations. The study highlights the potential of lonsdaleite for various applications due to its exceptional mechanical properties. The report also includes a comparison of the stiffness matrix components and bulk modulus, demonstrating lonsdaleite's enhanced uniaxial strength properties. The results indicate that lonsdaleite could be a significant advancement in material science, offering a combination of properties that rivals or surpasses those of diamond.

Lonsdaleite – A material stronger and stiffer than diamond
Li Qingkun,a,⇑ Sun Yi,b Li Zhiyuanc and Zhou Yua
aInstitute for Advanced Ceramics, Harbin Institute of Technology, Harbin 150001, People’s Republic of China
bThe Department of Astronautics Science and Mechanics, Harbin Institute of Technology, Harbin 150001, People’s Republi
cInstitute of Electronic Engineering, Heilongjiang University, Harbin 150080, People’s Republic of China
Received 26 March 2011; accepted 9 April 2011
Available online 13 April 2011
Based on first-principles calculations, we demonstrate that lonsdaleite exhibits many excellent static mechanical proper
instance, the compressive strength, coefficient of stiffness and Young’s modulus of lonsdaleite all exceed the correspondin
diamond. Moreover, the bulk modulus of lonsdaleite is as good as that of diamond, and its tensile strength is similar to tha
mond. Therefore, our results suggest that lonsdaleite is a stronger and stiffer naturally occurring substance than diamond
Ó 2011 Acta Materialia Inc. Published by Elsevier Ltd. All rights reserved.
Keywords: Lonsdaleite; Diamond; Stress–rupture density functions; Carbon
Diamond, a naturally occurring substance, is not
only considered to be the hardest material known [1–3],
but also presents excellent compressive strength [4,5], ten-
sile strength [3,5–7],Young’s modulus [1,8,9]and bulk
modulus [10].Over the past decade,there have been a
numberof reportsof materialsthat exhibithardness
and stiffnessclose to thatof diamond.For example,
experiments showed that cubic and wurtzite BN nano-
composites exhibit high hardness of 85 GPa [11],close
to the 70–100 GPa of diamond [12,13]. Theoretical and
experimental results demonstrated that C3N 4 exhibits a
hardness ofabout 85 GPa,rivalling thatof diamond
[14]. Composite materials created by mixing particles of
barium titanate and tin show high viscoelastic modulus
(Young’s modulus) close to 10,000 GPa [8], significantly
greater than the Young’s modulus of diamond,
1207 GPa [7]. Acetylenic molecular rods have a Young’s
modulus around 40 times larger than that of diamond
[1]. Although the new records of mechanicalproperties
were gradually reported, it is still difficult to find a mate-
rial with a combination of mechanical properties that riv-
als or exceeds that of diamond.
Lonsdaleite (hexagonal diamond), a natural substance
[15], has been attracting much attention because of its po-
tential excellent mechanical properties [3,16]. Lonsdaleite
is a carbon-based materialwith a hexagonalcrystallo-
graphic structure [3,17], and can be synthesized like dia-
mond under high static pressure and high temperature
[18]. A recent theoretical analysis has predicted lonsdale-
ite to have a higher indentation strength than diamond
[3], which meansthat lonsdaleitemight exhibit the
much-sought-after combination mechanical properties.
In this work, the mechanical properties of lonsdaleite,
including stiffness matrix, Young’s modulus, bulk mod-
ulus, compressive strength and tensile strength,have
been carefully calculated by a first-principles method.
Based on an analysis of the crystallographic structure,
we discuss the origin of lonsdaleite’s excellent mechani-
cal properties. Furthermore, the prospects for the appli-
cation of lonsdaleite are also discussed.
The structure-optimization and mechanical-property
calculations for lonsdaleite were performed using the CA-
STEP package based on the first-principles norm-con-
serving pseudopotentialapproach [19,20].For all the
calculations,the exchange–correlation potentialof the
generalized gradient approximation (GGA) with the Per-
dew–Burke–Ernzerhof (PBE) density functional [21] was
used. The energy-cutoff was set at 600 eV, and the maxi-
mum energy tolerancefor geometryoptimization
was <1.0 105 eV. For the structure-optimization and
mechanical-propertycalculationsof lonsdaleite,6
8 6 Monkhorst–Pack K-points [22]were adopted in
an 8-atom rectangularsolid supercell.Corresponding
calculations for diamond as a reference materialwere
performed,using either 6 8 6 Monkhorst–Pack
K-points [22]in a 12-atom rectangular solid supercell,
or 8 8 8 Monkhorst–Pack K-points in a 4-atom cu-
bic supercell according to the orientation of the diamond.
These supercellsof lonsdaleiteand diamond are
illustrated in Figure 1a–c, respectively. It should be noted
1359-6462/$ - see front matter Ó 2011 Acta Materialia Inc. Published by Elsevier Ltd. All rights reserved.
doi:10.1016/j.scriptamat.2011.04.013
⇑Corresponding author.Tel.: [phone];fax: +086 451
86403725; e-mail: [e-mail]
Available online at www.sciencedirect.com
Scripta Materialia 65 (2011) 229–232
www.elsevier.com/locate/scriptamat

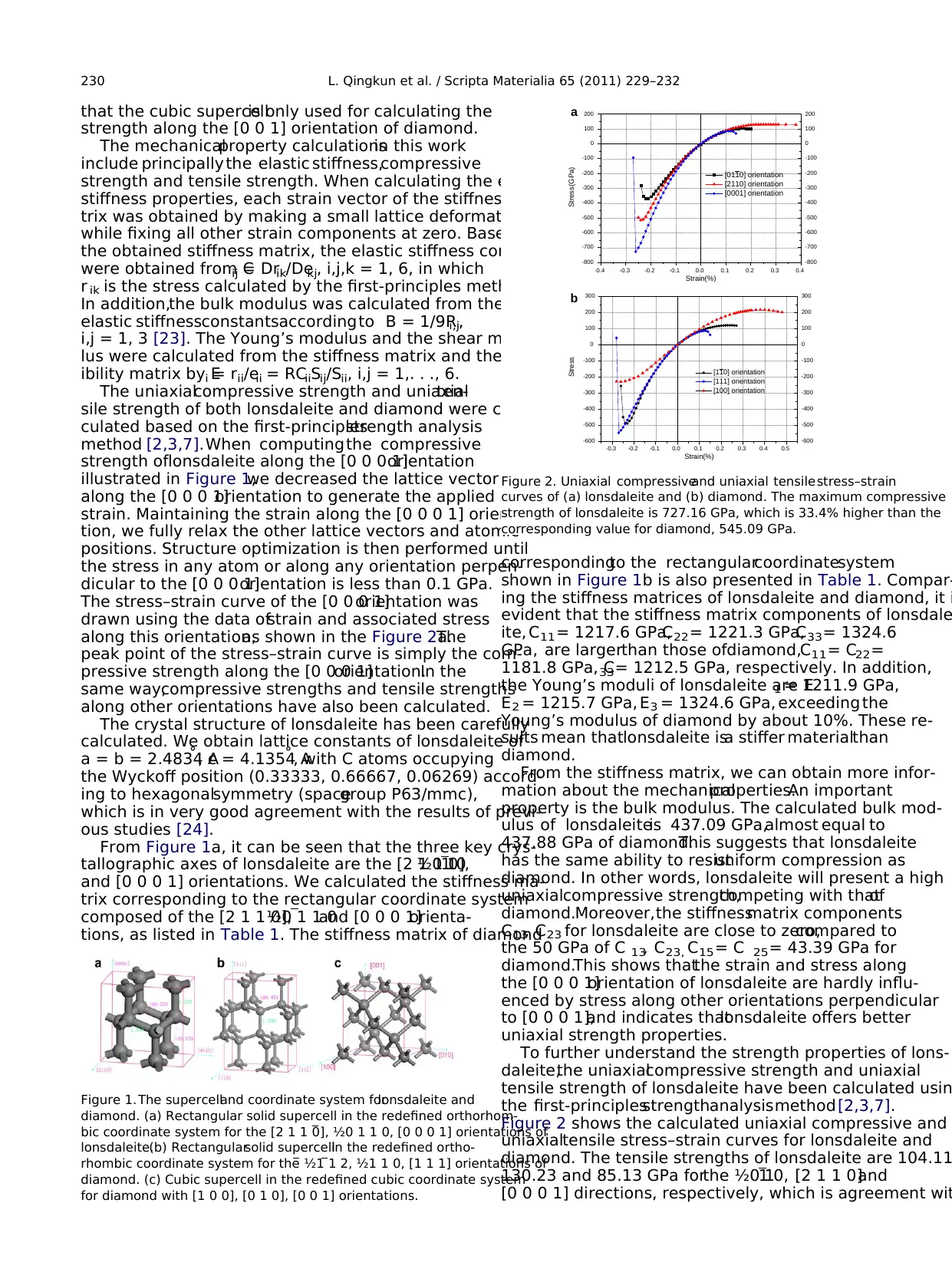
that the cubic supercellis only used for calculating the
strength along the [0 0 1] orientation of diamond.
The mechanicalproperty calculationsin this work
include principally the elastic stiffness,compressive
strength and tensile strength. When calculating the elastic
stiffness properties, each strain vector of the stiffness ma-
trix was obtained by making a small lattice deformation,
while fixing all other strain components at zero. Based on
the obtained stiffness matrix, the elastic stiffness constants
were obtained from Cij = Drik/Dekj, i,j,k = 1, 6, in which
r ik is the stress calculated by the first-principles method.
In addition,the bulk modulus was calculated from the
elastic stiffnessconstantsaccordingto B = 1/9Ri,j,
i,j = 1, 3 [23]. The Young’s modulus and the shear modu-
lus were calculated from the stiffness matrix and the flex-
ibility matrix by Ei = r ii/eii = RCiiSij/Sii, i,j = 1,. . ., 6.
The uniaxialcompressive strength and uniaxialten-
sile strength of both lonsdaleite and diamond were cal-
culated based on the first-principlesstrength analysis
method [2,3,7].When computingthe compressive
strength oflonsdaleite along the [0 0 0 1]orientation
illustrated in Figure 1,we decreased the lattice vector
along the [0 0 0 1]orientation to generate the applied
strain. Maintaining the strain along the [0 0 0 1] orienta-
tion, we fully relax the other lattice vectors and atomic
positions. Structure optimization is then performed until
the stress in any atom or along any orientation perpen-
dicular to the [0 0 0 1]orientation is less than 0.1 GPa.
The stress–strain curve of the [0 0 0 1]orientation was
drawn using the data ofstrain and associated stress
along this orientation,as shown in the Figure 2a.The
peak point of the stress–strain curve is simply the com-
pressive strength along the [0 0 0 1]orientation.In the
same way,compressive strengths and tensile strengths
along other orientations have also been calculated.
The crystal structure of lonsdaleite has been carefully
calculated. We obtain lattice constants of lonsdaleite of
a = b = 2.4834 A˚, c = 4.1354 A˚, with C atoms occupying
the Wyckoff position (0.33333, 0.66667, 0.06269) accord-
ing to hexagonalsymmetry (spacegroup P63/mmc),
which is in very good agreement with the results of previ-
ous studies [24].
From Figure 1a, it can be seen that the three key crys-
tallographic axes of lonsdaleite are the [2 1 1 0],½0 11 0
and [0 0 0 1] orientations. We calculated the stiffness ma-
trix corresponding to the rectangular coordinate system
composed of the [2 1 1 0],½0 1 1 0and [0 0 0 1]orienta-
tions, as listed in Table 1. The stiffness matrix of diamond
correspondingto the rectangularcoordinatesystem
shown in Figure 1b is also presented in Table 1. Compar-
ing the stiffness matrices of lonsdaleite and diamond, it i
evident that the stiffness matrix components of lonsdale
ite, C 11= 1217.6 GPa,C 22= 1221.3 GPa,C 33= 1324.6
GPa, are largerthan those ofdiamond,C 11= C22=
1181.8 GPa, C33= 1212.5 GPa, respectively. In addition,
the Young’s moduli of lonsdaleite are E1 = 1211.9 GPa,
E 2 = 1215.7 GPa, E 3 = 1324.6 GPa, exceeding the
Young’s modulus of diamond by about 10%. These re-
sults mean thatlonsdaleite isa stiffer materialthan
diamond.
From the stiffness matrix, we can obtain more infor-
mation about the mechanicalproperties.An important
property is the bulk modulus. The calculated bulk mod-
ulus of lonsdaleiteis 437.09 GPa,almost equal to
437.88 GPa of diamond.This suggests that lonsdaleite
has the same ability to resistuniform compression as
diamond. In other words, lonsdaleite will present a high
uniaxialcompressive strength,competing with thatof
diamond.Moreover,the stiffnessmatrix components
C 13, C 23 for lonsdaleite are close to zero,compared to
the 50 GPa of C 13, C 23, C 15= C 25= 43.39 GPa for
diamond.This shows thatthe strain and stress along
the [0 0 0 1]orientation of lonsdaleite are hardly influ-
enced by stress along other orientations perpendicular
to [0 0 0 1],and indicates thatlonsdaleite offers better
uniaxial strength properties.
To further understand the strength properties of lons-
daleite,the uniaxialcompressive strength and uniaxial
tensile strength of lonsdaleite have been calculated usin
the first-principlesstrengthanalysismethod [2,3,7].
Figure 2 shows the calculated uniaxial compressive and
uniaxialtensile stress–strain curves for lonsdaleite and
diamond. The tensile strengths of lonsdaleite are 104.11
130.23 and 85.13 GPa forthe ½0 11 0, [2 1 1 0]and
[0 0 0 1] directions, respectively, which is agreement wit
Figure 1.The supercelland coordinate system forlonsdaleite and
diamond. (a) Rectangular solid supercell in the redefined orthorhom-
bic coordinate system for the [2 1 1 0], ½0 1 1 0, [0 0 0 1] orientations of
lonsdaleite.(b) Rectangularsolid supercellin the redefined ortho-
rhombic coordinate system for the ½1 1 2, ½1 1 0, [1 1 1] orientations of
diamond. (c) Cubic supercell in the redefined cubic coordinate system
for diamond with [1 0 0], [0 1 0], [0 0 1] orientations.
-0.4 -0.3 -0.2 -0.1 0.0 0.1 0.2 0.3 0.4
-800
-700
-600
-500
-400
-300
-200
-100
0
100
200
-800
-700
-600
-500
-400
-300
-200
-100
0
100
200
[0110] orientation
[2110] orientation
[0001] orientation
Stress(GPa)
Strain(%)
-0.3 -0.2 -0.1 0.0 0.1 0.2 0.3 0.4 0.5
-600
-500
-400
-300
-200
-100
0
100
200
300
[110] orientation
[111] orientation
Stress
Strain(%)
-600
-500
-400
-300
-200
-100
0
100
200
300
[100] orientation
a
b
Figure 2. Uniaxial compressiveand uniaxial tensilestress–strain
curves of (a) lonsdaleite and (b) diamond. The maximum compressive
strength of lonsdaleite is 727.16 GPa, which is 33.4% higher than the
corresponding value for diamond, 545.09 GPa.
230 L. Qingkun et al. / Scripta Materialia 65 (2011) 229–232

theoreticalcalculations[3]. Although this maximum
strength value 130.23 GPa is considerably less than the
highest value for diamond, 220 GPa in the [1 0 0] orienta-
tion of the cubic coordinate system [3,5,7] shown in the
Figure 1c,it is still higher than the tensile strength of
many other high-strength materials,such as 84.1 GPa
for C-BN [13],90.6 GPa for W-BN [3,13]and 63 GPa
[25] or 100–120 GPa [26] for carbon nanotubes. The result
further demonstrates the high strength of lonsdaleite.
The most attractive feature appears when lonsdaleite
was compressed. As can been seen from the stress–strain
relations in Figure 2a, the compressive strengths of lons-
daleiteare 727.16,516.33and 369.66 GPafor the
[0 0 0 1],[2 1 1 0]and ½0 11 0 directions,respectively,
which shows an excellent capability to resist compres-
sion.In particular,the maximum compressive strength
of lonsdaleite achieved, i.e. 727.16 GPa, is 33.4% higher
than the corresponding value for diamond, 545.09 GPa,
obtained from Figure 2b (in Ref.[4],this strength is
410–490 GPa). These results mean that lonsdaleite could
be the strongest naturally occurring substance on earth.
From all the results calculated above, it is clear that the
lonsdaleite not only shows higher compressive strength
and stiffness than diamond, but also shows bulk modulus
and tensile strength close to those of diamond. Further-
more,we also note from the literature that lonsdaleite
shows excellent hardness,higher than that of diamond
[3].All the above-mentioned mechanicalproperties are
listed in Table 1, which shows that almost all the conven-
tional static mechanical properties of lonsdaleite exceed,
or match, those of diamond. These mechanical properties
suggest that lonsdaleite could find application in many
areas of high-pressure research. For example, lonsdaleite
anvil-cells could replace diamond anvil-cells [27–29]to
generate more extreme pressures in order to compress
small pieces of material for scientific experiments.
To understand thoroughly the properties of lonsdale-
ite, we explored the origin of its outstanding mechanical
properties. We first analyzed the bond structure of lons-
daleite. From Figure 1, it can be seen that two different
carbon–carbon bond lengths appear in lonsdaleite. The
bond length along the [0 0 0 1]orientation,referred to
as the major bond, is 1.550 A˚, a little larger than the bond
length in diamond, 1.528 A˚. The bond length along other
orientations, referred to as the minor bond, is 1.526 A˚ for
lonsdaleite, which slightly less than that of diamond. In
addition,in lonsdaleite,the bond angles between the
bonds parallel to the [0 0 0 1] orientation and any other
bonds are 109.88°, the other bond angles are 109.06°, ve
close to 109.47° in diamond. Thos means that lonsdaleite
possessesfeaturestypical of sp3 bond interactions,
although infinitesimal differences exist between the bond
lengths and angles of lonsdaleite and diamond.
Furthermore,lonsdaleite also presentsa more or-
dered crystalstructure,in the following two respects.
(i) The [0 0 0 1] orientation is not only the close-packed
direction, but is also the crystallographic 3-fold symme-
try axis. This structure causes the packing density along
the [0 0 0 1]orientation to increase to 0.484 atom A˚ 1 ,
which is higher than the packing density of 0.398 atom
A˚ 1 along the [1 1 1]orientation in diamond.As a re-
sult, the higher packing density will increase the ability
to support an axialload along the [0 0 0 1]orientation.
(ii) The close-packed direction [0 0 0 1] is perpendicular
to slip plane (0001); at the same time, it is also parallel
to slip planes (2 1 1 0) and ð0 11 0Þ. This relationship be-
tween the close-packed direction and the slip planes
makes lonsdaleite fracture easily rather than slide along
any planes inclined to the [0 0 0 1] orientation.
Therefore,the excellentmechanicalpropertiesof
lonsdaleite mainly originate from two sources:strong
sp3 bond interaction and a more ordered crystalstruc-
ture.In order to confirm this,the bond length–strain
relation of lonsdaleite under [0 0 0 1] orientation uniax-
ial compression—as well as bond length–strain relation
of diamond under [1 1 1]orientation uniaxialcompres-
sion—have been calculated, as shown in Figure 3.
Figure 3 shows that lonsdaleite and diamond exhibit
similar bond length–strain relationships during the com-
pressive process. For convenience, we again refer to the
bonds along the [1 1 1] orientation of diamond as major
bonds, and other bonds as minor bonds. Obviously, the
Table 1.Stiffness, strength, and hardness properties of lonsdaleite and diamond.
Properties Lonsdaleite Diamond
Young’s modulus E½2 1 1 0¼ 1211:94 GPa
E½0 11 0
¼ 1215:67 GPa
E½0 0 0 1¼ 1324:57 GPa
E½1 0 0¼ 1068:89 GPa
E½1 1 0
¼ 1170:23 GPa
E½1 1 1¼ 1208:42 GPa
Stiffness matrix C 11= 1217.58 GPa, C22= 1221.33 GPa,
C 33= 1324.57GPa,
C 12= 83.02 GPa, C13= 1.20 GPa,
C 23= 0.97 Pa, C44= C55= 480.35 GPa,
C 66= 567.08 GPa
C 11= C22= 1181.79 GPa, C33= 1212.472 GPa,
C 44= C55= 519.5834 GPa,
C 66= 550.2648 GPa C12= 81.2605 GPa,
C 13= C23= 50.57905 GPa, C15= C 25= 43.39012 GPa,
C 34= 43.3901227 GPa,
Bulk modulus B0 = 437.09748 GPa B0 = 437.8766 GPa
Tensile strength r ½0 1 1 0
¼ 104:11 GPa
r ½2 1 1 0¼ 130:23 GPa
r ½0 0 0 1¼ 85:13 GPa
r ½1 0 0¼ 217:32 GPa
r ½1 1 0
¼ 121:09 GPa
r ½1 1 1¼ 86:01 GPa
Compressive strength r ½0 1 1 0
¼ 369:66 GPa
r ½2 1 1 0¼ 516:33 GPa
r ½0 0 0 1¼ 727:16 GPa
r ½1 0 0¼ 229:13 GPa
r ½1 1 0
¼ 487:45 GPa
r ½1 1 1¼ 545:09 GPa
Hardness H v[0001]= 152 GPa [3] H v[111]= 97 GPa[3]
L. Qingkun et al. / Scripta Materialia 65 (2011) 229–232 231

major bond lengths of both lonsdaleite and diamond sig-
nificantly decrease with increasing compressive strain.
Lonsdaleite was broken when the major bond length de-
creased to a critical length of 1.27 A˚. This critical bond
length is the same as the critical major bond length of dia-
mond. This result suggests that 1.27 A˚ is the compressive
limitation for maintaining the stability of the C–C sp3
bond. It also further confirms that the failure under com-
pression of both lonsdaleite and diamond is mainly due to
excessive compression of the major sp3 bonds.
On the other hand, due to its ordered crystallographic
structure, lonsdaleite exhibits various unique phenomena
during uniaxialcompression.These specialphenomena
include: (i) the minor bond length of lonsdaleite is in the
range 1.48–1.52 A˚, which is always less than the corre-
sponding valuefor diamond.When the compressive
strain is 25%, the minor bond length difference between
lonsdaleite and diamond is up to 0.04 A˚. (ii) the minor
bond length of lonsdaleitedecreaseswith increasing
strain untilthe strain is over 23%,and then the bond
length of the minor bond begins to increase gradually.
The minimum value of the minor bond length for lons-
daleite appeared ata higher strain than for diamond.
(iii) Before lonsdaleite breaks, its minor bond is always
under compression,unlike the minor bond of diamond
which is tensile under large uniaxial compressive strain.
Taken altogether,the minor bonds of lonsdaleite have
been more efficiently compressed. These phenomena im-
ply that lonsdaleite possesses higher stability to resist uni-
axial compression,which clearly enhancesits uniaxial
compressive strength.
In summary,the strength and stiffness properties of
lonsdaleite have been carefully calculated based on a
first-principlesmethod.Our calculation resultsshow
that lonsdaleite exhibits excellent mechanical properties,
as follows (i) the maximum stiffness coefficient of lons-
daleite is 1324.57 GPa, the maximum Young’s modulus
is 1324.57 GPa, and the maximum compressive strength
is 727.16 GPa,which are allabove the corresponding
values for diamond; (ii) the bulk modulus of lonsdaleite
is 437.09 GPa, which is as good as the bulk modulus of
diamond; (iii) the maximum tensile strength of lonsdale-
ite is 130.23 GPa, which is close to that of diamond. We
also note thatlonsdaleite hasa superiorindentation
strength,exceeding the corresponding valuesfor dia-
mond based on theoreticalprediction in the literature.
Therefore, we predict that lonsdaleite might be a stron-
ger, stifferand hardernaturally occurring substance
than diamond,and hence could have greatpotential
for application in high-pressure research.
[1] L. Itzhaki et al., Angew. Chem. Int. Edit. 44 (2005) 7432.
[2] Y. Zhang,H. Sun, C. Chen,Phys.Rev. Lett. 94 (2005)
145505.
[3] Z.C. Pan et al., Phys. Rev. Lett. 102 (2009) 055503.
[4] A. David, J. Nelson, A.L. Ruoff, J. Appl. Phys. 50 (1979) 276
[5] X.G. Luo et al., J. Phys. Chem. C. 114 (2010) 17851.
[6] Y. Zhang, H. Sun, C.F. Chen, Phys. Rev. B. 73 (2006) 1441
[7] R.H. Telling et al., Phys. Rev. Lett. 84 (2000) 5160.
[8] T. Jaglinski et al., Science 315 (2007) 620.
[9] D.J. Weidner,Y.B. Wang,M.T. Vaughan,Science 266
(1994) 419.
[10] E. Ziambaras,E. Schroder,Phys. Rev. B. 68 (2003)
064112.
[11] N. Dubrovinskaia etal., Appl. Phys. Lett. 90 (2007)
101912.
[12] D.W. He et al., Appl. Phys. Lett. 81 (2002) 643.
[13] R.F. Zhang, S. Veprek, A.S. Argon, et al., Phys. Rev. B.
77 (2008) 172103.
[14] J.L. He et al., Appl. Phys. Lett. 88 (2006) 101906.
[15] V.T.Dubinchuk,S.K. Simakov,V.A. Pechnikov,Dokl.
Earth Sci. 430 (2010) 40.
[16] H. Chen, W.Y. Zhang,Z.L. Wang, J. Phys. Condes.
Matter. 16 (2004) 741.
[17] F.P. Bundy, J.S. Kasper, J. Chem. Phys. 46 (1967) 3437.
[18] H.K.He, T. Sekine,T. Kobayashi,Appl. Phys.Lett. 81
(2002) 610.
[19] D.R.Hamann,M. Schluter,C. Chiang,Phys.Rev. Lett.
43 (1979) 1494.
[20] J.S. Lin, Phys. Rev. B. 47 (1993) 4174.
[21] J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77
(1996) 3865.
[22] H.J. Monkhorst, J.D. Pack, Phys. Rev. B. 13 (1976) 5188.
[23] M. Hebbache, Solid State Commun. 110 (1999) 559.
[24] S.Q. Wang, H.Q. Ye, J. Phys. Condes. Matter. 15 (2003)
L197.
[25] M.F. Yu et al., Science 287 (2000) 637.
[26] S. Ogata, Y. Shibutani, Phys. Rev. B. 68 (2003) 165409.
[27] D.K. Bradley et al., Phys. Rev. Lett. 102 (2009) 075503.
[28] R.S. McWilliams et al., Phys. Rev. B. 81 (2010) 014111.
[29] M.I. Eremets et al., Appl. Phys. Lett. 87 (2005) 141902.
-0.30 -0.25 -0.20 -0.15 -0.10 -0.05 0.00
1.25
1.30
1.35
1.40
1.45
1.50
1.55
Band length (Å)
Strain(%)
Major bond length for diamond
Major bond length for lonsdaleite
Minor bond length for diamond
Minor bond length for lonsdaleite
Figure 3.Calculated bond length–strain curves for [0 0 0 1]compres-
sion of lonsdaleite,and [1 1 1]orientation compression of diamond.
The figureshowsthat the minor bonds of lonsdaleitehave been
compressed more efficiently.
232 L. Qingkun et al. / Scripta Materialia 65 (2011) 229–232