Aviation Statistics and Decision Making

This study material covers topics such as normal distribution, skewness, Likert scale, and incidents of unruly passengers in aviation. It explains the concepts with examples and provides annotated bibliography for further reading. The subject is aviation statistics and decision making, and the course code, course name, and college/university are not mentioned.

Running head: AVIATION STATISTICS AND DECISION MAKING
Aviation Statistics and Decision Making
Name of the Student:
Name of the University:
Author’s note:

1AVIATION STATISTICS AND DECISION MAKING
Table of Contents
Answer 1:-.......................................................................................................................................2
a) Normal Distribution:.............................................................................................................2
a) Positivity skewed distribution:.............................................................................................3
b) Negatively skewed distribution:........................................................................................5
Answer 2:-.......................................................................................................................................6
Answer 3:.......................................................................................................................................10
Annotated Bibliography:...............................................................................................................16

2AVIATION STATISTICS AND DECISION MAKING
Answer 1:-
a) Normal Distribution:
Normal or Gaussian distribution is a continuous probability distribution. Normal
distribution is such a type of distribution where random variables are normally distributed. The
normal distribution is informally bell shaped curve in nature. The probability density of the
normal distribution is given by-
Here, μ= The mean or average or expectation of the distribution.
σ = Standard deviation of the distribution.
σ2 = Variance of the distribution.
Normal distribution is symmetric in nature that means it has equal concentration of mass
towards both the sides of the curve. Symmetry means that one-half of the distribution is a minor
image of the other half. The skewness of normal distribution is 0 (Harvey and Siddique 2000).
We calculate the skewness of other curves with respect to normal distribution.

3AVIATION STATISTICS AND DECISION MAKING

4AVIATION STATISTICS AND DECISION MAKING
An ideal normal curve shows symmetricity in both part of mass-concentration (Hoeffding
1948).
Many real life measures such as height, weight and IQ are encountered as normally
siatributed.
Skewness:
Skewness is an asymmetry measure of the probability distribution of real valued random
variables with respect to its mean. The skewness could be positive or negative. Skewness
does not determine the relevance of mean and median. However, skewness decides the
symmetricity or asymmmetricity of the curve.
Pearson’s first measure of skewness coefficient is defined as-
mean−mode
standard deviation
Pearson’s second measure of skewness coefficient is defined as-
3(mean−median)
standard deviation

5AVIATION STATISTICS AND DECISION MAKING
a) Positivity skewed distribution:
Positively skewed distribution infers that its right tail is longer and fatter than its left tail.
It could be discrete or multimodal distribution. The mass is concentrated on the left side
of the figure. Positively skewed distribution is sometimes called as “right-tailed” or
“skewed to the right”. Mean is skewed to the right of a typical centre of the data. There is
a long tail in positive direction on the number line and the mean is also to the right side of
the peak.
In this case, mode < median < mean.

6AVIATION STATISTICS AND DECISION MAKING
A plot of secondary data of Household income of USA indicates the positively
skewed distribution.
b) Negatively skewed distribution:
In case of negatively skewed distribution, mass of distribution is concentrated on the right
side of the figure. The distribution is also known as “left skewed” or “left-tailed” or
“skewed to the left”. A left-skewed distribution usually appears to be a right-leaning
curve. Mean is skewed to the left of a typical centre of the data. There is a long tail in the
negative direction of the number line and the mean is also to the left of the peak.

7AVIATION STATISTICS AND DECISION MAKING
In this case, mode > median > mean.
A plot of secondary data of Household income of each percentile of 2011 indicates the
negatively skewed distribution.

8AVIATION STATISTICS AND DECISION MAKING
Answer 2:-
The scale used in question number 2 is “Liker-scale”. The data is collected in three
samples. The data is qualitative in nature. Specifically, this categorical data is ordinal in nature
(Allen and Seaman 2007) as the categories are normally ordered in this case.
Actually ordinal data is a statistically categorical data where variables have natural and
ordered categories and the distances between categories are unknown. It could be classified as
“very unhappy, unhappy, OK, happy and very happy” or “strongly disagree, disagree, don’t
know, agree and strongly disagree”.
Our chosen “Likert” scale is defined as-
1. Very enjoyable.
2. Enjoyable.
3. OK I guess.
4. Painful.
5. Very painful.
Actually ordinal data could be described and ranked using comparative objectives. However,
it can only be described in terms of comparative magnitude only.
Nominal data is also a special type of categorical data used to measure simple qualitative
categories such as male/female. It could only be counted to compare objectives such as longer or
shorter, heavier or lighter, more or less. On the other hand, interval and ratio data are almost
identical. Interval and ratio datasets focuses at equal intervals. The ratio data follows the scale

9AVIATION STATISTICS AND DECISION MAKING
rules such as addition, multiplication, subtraction and division ignoring some exceptions (Agresti
2010).
The ordinal data reflects the true scenario of characteristics of a population whether
sample is large or small. The larger our sample is, the more likely it is to be representatives.
Graphical plots such as bar plot, scatter plot, histogram, pie-chart could be drawn by ordinal data
(Agresti and Kateri 2011). Interval or ratio data properly indicates the aspects of descriptive
statistics like mean, median, mode, quartiles and mode. However, categorical data such as
nominal or ordinal data do not provide exact reflection of the data in terms of summary or
descriptive statistics.
The measures of dispersion are also well incorporated by interval and ratio data. It
involves skewness and Kurtosis, mean deviation about mean, mean deviation about median,
variance, standard deviation, coefficient of variance, range and inter-quartile range. However,
leveling the ordinal data by 1, 2, 3, 4 and 5, or so on, we can bring numerical approach in
categorical variables such as nominal or ordinal. Parametric tests such as t-test, z-test, F-test and
p-value calculation for hypothesis testing id meaningful for interval and ratio data.
Oppositely, the formation of frequency and percentile table and draw calculation from
these are more meaningful for ordinal and nominal data rather than interval or ratio data. Non
parametric tests such as Signed ranked test, Wilcoxon rank test, chi-square tests are applicable
for ordinal as well as nominal data (Velleman and Wilkinson 1993). P-value calculation and
hypothesis testing is not relevant in this matter.

10AVIATION STATISTICS AND DECISION MAKING
Answer 3:
a) This is a data of incidents including “unruly passengers” collected by FAA for each year
between 1995 and 2016. First, we present the actual secondary data in the following.
Case Year
Total number of
incidents
1 1995 146
2 1996 184
3 1997 237
4 1998 204
5 1999 226
6 2000 255
7 2001 305
8 2002 279
9 2003 286
10 2004 310
11 2005 205
12 2006 137
13 2007 153
14 2008 124
15 2009 139
16 2010 128
17 2011 155
18 2012 183
19 2013 149
20 2014 147
21 2015 105
22 2016 99
Total number of incidents
Mean 188.9090909
Standard Error 13.96872033
Median 169
Mode #N/A

11AVIATION STATISTICS AND DECISION MAKING
Population Standard Deviation 65.51910597
Sample Standard Deviation 68.63906339
Sample Variance 4292.753247
Kurtosis -0.901885934
Skewness 0.570283527
Range 211
Minimum 99
Maximum 310
Sum 4156
Count 22
Largest(1) 310
Smallest(1) 99
Confidence Level(95.0%) 29.04954408
Total number of incidents
Frequency Percent Valid Percent Cumulative Percent
Valid 99.00 1 4.5 4.5 4.5
105.00 1 4.5 4.5 9.1
124.00 1 4.5 4.5 13.6
128.00 1 4.5 4.5 18.2
137.00 1 4.5 4.5 22.7
139.00 1 4.5 4.5 27.3
146.00 1 4.5 4.5 31.8
147.00 1 4.5 4.5 36.4
149.00 1 4.5 4.5 40.9
153.00 1 4.5 4.5 45.5
155.00 1 4.5 4.5 50.0
183.00 1 4.5 4.5 54.5
184.00 1 4.5 4.5 59.1
204.00 1 4.5 4.5 63.6
205.00 1 4.5 4.5 68.2
226.00 1 4.5 4.5 72.7
237.00 1 4.5 4.5 77.3
255.00 1 4.5 4.5 81.8
279.00 1 4.5 4.5 86.4
286.00 1 4.5 4.5 90.9
305.00 1 4.5 4.5 95.5

12AVIATION STATISTICS AND DECISION MAKING
310.00 1 4.5 4.5 100.0
Total 22 100.0 100.0
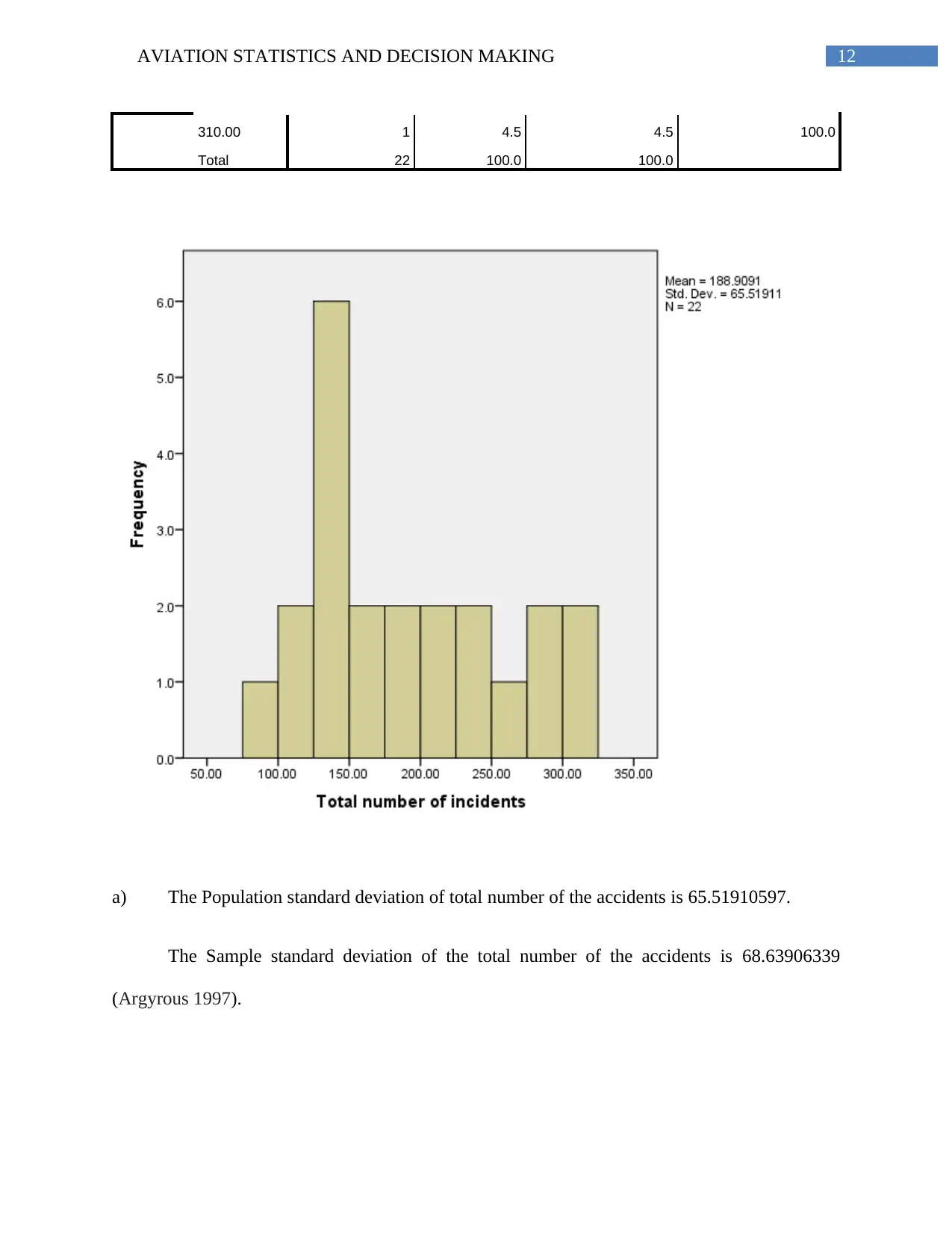
a) The Population standard deviation of total number of the accidents is 65.51910597.
The Sample standard deviation of the total number of the accidents is 68.63906339
(Argyrous 1997).

13AVIATION STATISTICS AND DECISION MAKING
b) The mean of the total number of the accidents is 188.9090909.
The median of the total number of the accidents is 169 (Oja 1983).
The mode of the total number of the accidents is not defined properly according to the
calculation. However, it lies in 125 to 150 with six time occurrences.
c) 0.570283527 is the measure of skewness of the incidents over years. Hence, the
distribution is slightly positively skewed (Brown 1997). Besides, one sample t-test shows the
significant p-value (0.0) that is less than 0.05. Therefore, we reject the null hypothesis of
normality of year wise data of total number of accidents. Hence, the distribution of incidents
over the years is not normally distributed. The evidence of slightly positive value of skewness
supports that consideration.
One Sample T-Test
One-Sample Statistics
N Mean Std. Deviation Std. Error Mean
Total number of incidents 22 188.9091 65.51911 13.96872
One-Sample Test
Test Value = 0
t df Sig. (2-
tailed)
Mean
Difference
95% Confidence Interval
of the Difference
Lower Upper
Total number of
incidents 13.524 21 .000 188.90909 159.8595 217.9586

14AVIATION STATISTICS AND DECISION MAKING
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
0
50
100
150
200
250
300
350
Total number of incidents
Total number of incidents

15AVIATION STATISTICS AND DECISION MAKING
The bar plots executed in MS excel and SPSS indicates the bar plot of year wise distribution of
number of accidents.

16AVIATION STATISTICS AND DECISION MAKING
Annotated Bibliography:
Agresti, A. and Kateri, M., 2011. Categorical data analysis. In International encyclopedia of
statistical science (pp. 206-208). Springer Berlin Heidelberg.
Agresti, A., 2010. Analysis of ordinal categorical data (Vol. 656). John Wiley & Sons.
Allen, I.E. and Seaman, C.A., 2007. Likert scales and data analyses. Quality progress, 40(7),
p.64.
Argyrous, G., 1997. Descriptive statistics on SPSS. In Statistics for Social Research (pp. 60-78).
Palgrave, London.
Brown, J.D., 1997. Skewness and kurtosis. Shiken: JALT testing and evaluation SIG
Newsletter, 1(1).
Harvey, C.R. and Siddique, A., 2000. Conditional skewness in asset pricing tests. The Journal of
Finance, 55(3), pp.1263-1295.
Hoeffding, W., 1948. A class of statistics with asymptotically normal distribution. The annals of
mathematical statistics, pp.293-325.
Oja, H., 1983. Descriptive statistics for multivariate distributions. Statistics & Probability
Letters, 1(6), pp.327-332.
Velleman, P.F. and Wilkinson, L., 1993. Nominal, ordinal, interval, and ratio typologies are
misleading. The American Statistician, 47(1), pp.65-72.

17AVIATION STATISTICS AND DECISION MAKING