University Game Theory Homework: Problem Set Solutions

This document provides comprehensive solutions to a game theory problem set, addressing various concepts such as dominant strategies, Nash equilibrium, and subgame perfect Nash equilibrium (SPNE). The solutions cover several game scenarios, including a classic game matrix, a coordination gam...Read More

Running head: BASICS OF GAME THEORY
Basics of Game Theory
Name of the Student:
Name of the University:
Author Note:

1BASICS OF GAME THEORY
Table of Contents
Answer 1....................................................................................................................................2
Answer 2....................................................................................................................................2
Answer 3....................................................................................................................................3
Answer 4 Part I...........................................................................................................................4
Answer 4 Part II. 1.....................................................................................................................4
Answer 4 Part II. 2.....................................................................................................................6
Answer 5 Part I...........................................................................................................................6
Answer 5 Part II.........................................................................................................................6
Answer 5 Part III........................................................................................................................7
Reference....................................................................................................................................8

2BASICS OF GAME THEORY
Answer 1
2
C D
1 C 9 9 -1 10
D 10 -1 0 0
In the above game, the dominant strategy for both the players (1,2) is (D,D) that is
(0,0). But there exist a Nash equilibrium which is (C,C) that means (9,9) is the pay of for the
two players (1,2).
Answer 2
2
L R
1
U 4 1 0 0
D 0 0 1 4
There exists pure Nash equilibrium in case of the given coordination game. Here, two
Nash equilibriums exist. The Nash strategies for the players (1,2) are (U,L) and (D,R)
(Webster).
2
L(q) R(1-q)
1 U(p) 4 1 0 0
D(1-p) 0 0 1 4
The probabilities are mentioned with the players’ strategy.

3BASICS OF GAME THEORY
 The expected payoff of player 1 at the equilibrium (U , L) = (4*q)+{0*(1-q)} = 4q
The expected payoff of player 2 at the equilibrium (U , L) = (1*p)+{0*(1-p)} = p
 The expected payoff of player 1 at the equilibrium (D , R) = {0*q}+{1*(1-q)}=1-q
The expected payoff of player 2 at the equilibrium (D , R) = (0*p)+{4*(1-p)} = 4(1-p)
Answer 3
The SPNE for the above game is (6,7) because the payoff (6,7) of the given strategy is
always preferred by both the players at every stage in the SPNE.
The SPNE for the above game is (1,0) because the payoff (1,0) of the given strategy is
always preferred by the player 1 over the strategy to continue where the payoff of player 1 is
0.
At the last node, if player 2 chooses to continue then the payoff is 5 and if the player
chooses to stop then the payoff is 6 which is greater than 5. That means the player 2 chooses
to stop. Now at the second last node if player 1 chooses to continue then the payoff is 4 and if

4BASICS OF GAME THEORY
Player-1
( 5-x x ) ( 0 0 )
Player-2
Offer
RejectAccept
the player chooses to stop then the payoff is 5 which is greater than 4. That means the player
1 chooses to stop and so on. Finally, at the first node player 1 will choose to stop as the
payoff from the strategy to stop is 1 which is greater than the payoff (0) from the strategy to
continue (Papadimitriou, Christos, and Piliouras).
Answer 4 Part I
If the player-2 offers x=0 to the player-1 then the player-1 will reject the offer as the
payoff for player-1 is 0 for both the moves and will threat player-2 by rejecting the offer
where the payoff for the player-2 is 0 which less than (5-x) as player-2 will not offer x=5 to
the player-1. Now, if the offer x>0 then the player-1 will accept the offer as the payoff is
greater for accepting the offer than to reject.
So, for x>0, SPNE of the game will end up by accepting the offer by player-1.
Answer 4 Part II. 1

5BASICS OF GAME THEORY
Player-1
( 200-y y)
( x 100-x )
Player-1
( 0 0 )
Offer
Offer
Accept
Accept Reject
Player-2
From the previous discussion, it is clear that the player-1 will reject the offer if x=0
and the payoff for both the player is 0. Now, the player-1 will accept the offer if x>0 and the
pay for the player-1 will be x which is greater than 0 which is the payoff for rejecting the
offer. Now, the player-2 will get the payoff “y” for accepting the offer and (100-x) for
offering. In this situation player-2 will accept the offer if y≥(100-x) otherwise the offer will
be rejected and player-1 accept the offer at x>0. In this case, player-1 will offer at y≥100
where player-2 will accept the offer and end the game.
So, for x>0 and y≥100, SPNE of the game will end up by accepting the offer by
player-2.

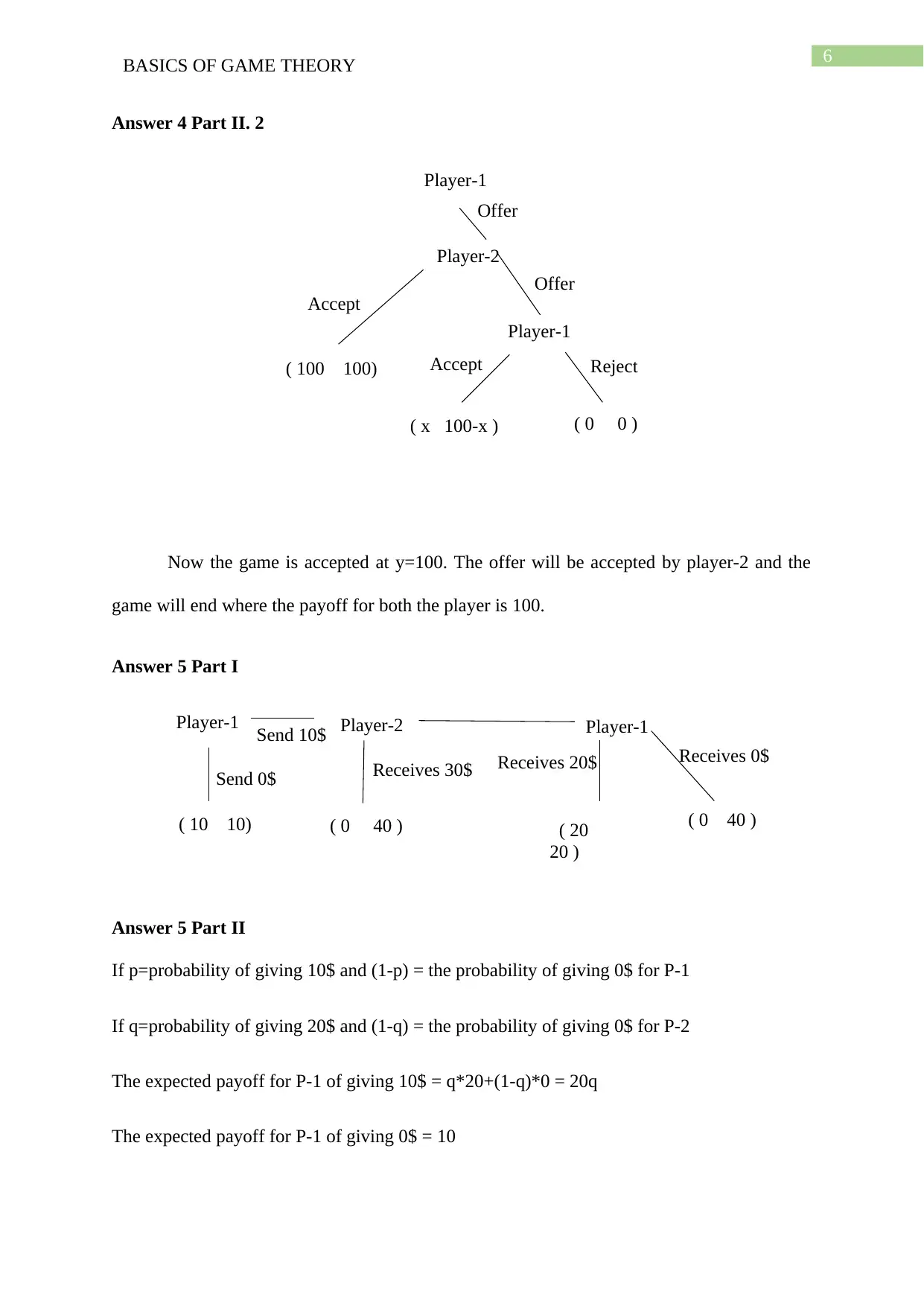
6BASICS OF GAME THEORY
Player-1
( 100 100)
( x 100-x )
Player-1
( 0 0 )
Offer
Offer
Accept
Accept Reject
Player-2
Player-1
( 10 10) ( 0 40 ) ( 0 40 )
Send 10$
Send 0$ Receives 30$ Receives 20$
Player-1
( 20
20 )
Receives 0$
Player-2
Answer 4 Part II. 2
Now the game is accepted at y=100. The offer will be accepted by player-2 and the
game will end where the payoff for both the player is 100.
Answer 5 Part I
Answer 5 Part II
If p=probability of giving 10$ and (1-p) = the probability of giving 0$ for P-1
If q=probability of giving 20$ and (1-q) = the probability of giving 0$ for P-2
The expected payoff for P-1 of giving 10$ = q*20+(1-q)*0 = 20q
The expected payoff for P-1 of giving 0$ = 10

7BASICS OF GAME THEORY
So, to encourage the P-1 to give 10$ necessary condition is 20q>10 that means q>0.5
(Bodford, Jessica and Kwan)
Hence the probability should be greater than 0.5 to give 20$ to the P-1.
Answer 5 Part III
The reason for giving 20$ to the player-1 is the received amount (30$) was higher
than the amount of giving (20$) that means the player-2 gets 10$ extra even if player-2 gives
20$ to the player-1. In case of, second games the player-2 ends up giving 0$ to the player-1
as the plyaer-2 is not getting any amount from player-1. This means in second case, if player-
2 gives 20$ to the player-1, player-2 will lose 20$. Hence the player-2 gives 20$ in the first
case and 0$ in the second case (Cartwright).

8BASICS OF GAME THEORY
Reference
Bodford, Jessica E., and Virginia SY Kwan. "A Game Theoretical Approach to Hacktivism:
Is Attack Likelihood a Product of Risks and Payoffs?." Cyberpsychology, Behavior, and
Social Networking 21.2 (2018): 73-77.
Cartwright, Edward. "A survey of belief-based guilt aversion in trust and dictator
games." Journal of Economic Behavior & Organization (2018).
Papadimitriou, Christos, and Georgios Piliouras. "From Nash Equilibria to Chain Recurrent
Sets: An Algorithmic Solution Concept for Game Theory." Entropy 20.10 (2018): 782.
Webster, Thomas J. Introduction to game theory in business and economics. Routledge,
2018.