Beta Decay: Energy Spectrum, Decay Constant, and Parity Conservation
VerifiedAdded on 2023/06/10
|9
|4054
|422
AI Summary
This article discusses the concept of beta decay, including its energy spectrum, decay constant, and parity conservation. It explains the different types of beta decay and their reduced half-life values. It also covers the shielding properties of alpha, beta, and gamma radiation.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.
Introduction
The concept of beta decay unites kinds of nuclear transformations: electron (β‾) decay,
positron (β⁺) decay and electron capture. About 900 beta-radioactive isotopes are known.
Only about 20 of them are natural, the rest were obtained by artificial methods. The
overwhelming majority of these isotopes are subject to β‾- decay. One electron is emitted in
each event of β‾- decay. Double beta decay, with two electrons(positrons) emitted in each
event, is theoretically possible, but has not been observed experimentally as yet (Detlafand
I︠A︡vorskiı̆, 1980).
Energy Spectrum of Beta-Decay
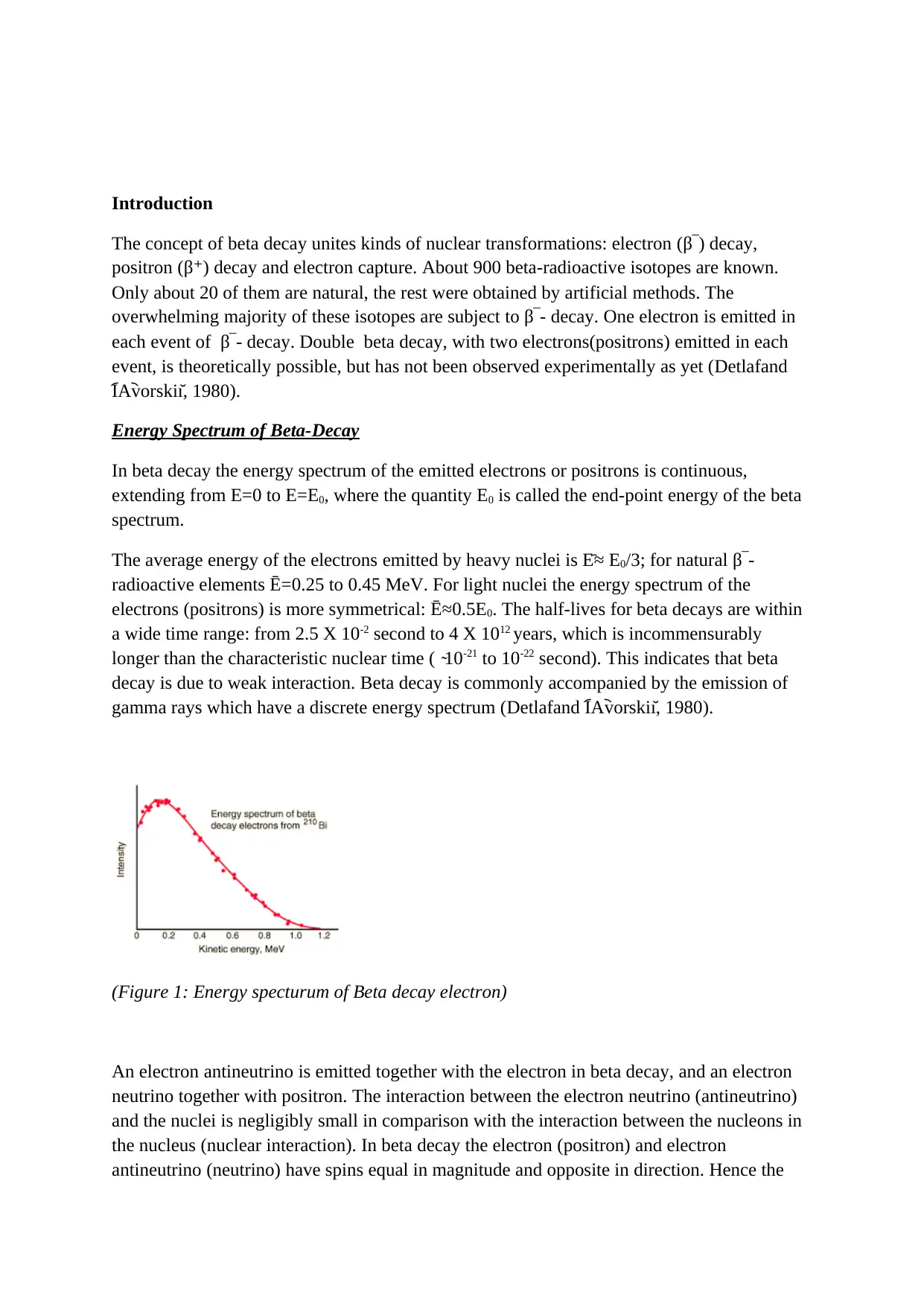
In beta decay the energy spectrum of the emitted electrons or positrons is continuous,
extending from E=0 to E=E0, where the quantity E0 is called the end-point energy of the beta
spectrum.
The average energy of the electrons emitted by heavy nuclei is Ē ≈ E0/3; for natural β‾-
radioactive elements Ē =0.25 to 0.45 MeV. For light nuclei the energy spectrum of the
electrons (positrons) is more symmetrical: Ē ≈0.5E 0. The half-lives for beta decays are within
a wide time range: from 2.5 X 10-2 second to 4 X 1012 years, which is incommensurably
longer than the characteristic nuclear time (̴ 10-21 to 10-22 second). This indicates that beta
decay is due to weak interaction. Beta decay is commonly accompanied by the emission of
gamma rays which have a discrete energy spectrum (Detlafand I︠A︡vorskiı̆, 1980).
(Figure 1: Energy specturum of Beta decay electron)
An electron antineutrino is emitted together with the electron in beta decay, and an electron
neutrino together with positron. The interaction between the electron neutrino (antineutrino)
and the nuclei is negligibly small in comparison with the interaction between the nucleons in
the nucleus (nuclear interaction). In beta decay the electron (positron) and electron
antineutrino (neutrino) have spins equal in magnitude and opposite in direction. Hence the
The concept of beta decay unites kinds of nuclear transformations: electron (β‾) decay,
positron (β⁺) decay and electron capture. About 900 beta-radioactive isotopes are known.
Only about 20 of them are natural, the rest were obtained by artificial methods. The
overwhelming majority of these isotopes are subject to β‾- decay. One electron is emitted in
each event of β‾- decay. Double beta decay, with two electrons(positrons) emitted in each
event, is theoretically possible, but has not been observed experimentally as yet (Detlafand
I︠A︡vorskiı̆, 1980).
Energy Spectrum of Beta-Decay
In beta decay the energy spectrum of the emitted electrons or positrons is continuous,
extending from E=0 to E=E0, where the quantity E0 is called the end-point energy of the beta
spectrum.
The average energy of the electrons emitted by heavy nuclei is Ē ≈ E0/3; for natural β‾-
radioactive elements Ē =0.25 to 0.45 MeV. For light nuclei the energy spectrum of the
electrons (positrons) is more symmetrical: Ē ≈0.5E 0. The half-lives for beta decays are within
a wide time range: from 2.5 X 10-2 second to 4 X 1012 years, which is incommensurably
longer than the characteristic nuclear time (̴ 10-21 to 10-22 second). This indicates that beta
decay is due to weak interaction. Beta decay is commonly accompanied by the emission of
gamma rays which have a discrete energy spectrum (Detlafand I︠A︡vorskiı̆, 1980).
(Figure 1: Energy specturum of Beta decay electron)
An electron antineutrino is emitted together with the electron in beta decay, and an electron
neutrino together with positron. The interaction between the electron neutrino (antineutrino)
and the nuclei is negligibly small in comparison with the interaction between the nucleons in
the nucleus (nuclear interaction). In beta decay the electron (positron) and electron
antineutrino (neutrino) have spins equal in magnitude and opposite in direction. Hence the
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

change in the spin of the nucleus equals zero. The continuous spectrum of beta decay is due
to the different distributions of energy between the electron (positron) and the electron
antineutrino (neutrino), the total energy of the two particles being equal to E0 (Detlafand
I︠A︡vorskiı̆, 1980).
According to the current concept, the electron (positron) and the electron antineutrino
(neutrino) do not exist in atomic nuclei but are formed at the instant of emission from the
nucleus as a result of weak interaction between the nucleons in the nucleus. Since new
particles are produced in the beta decay, the methods of non-relativistic quantum mechanics
are inapplicable to this process and the problem is dealt with the methods of quantum field
theory.
In the theory of beta decay, the production of an electron and an electron neutrino (positron
and electron neutrino) is treated as the result of the interaction between a nucleon of the
nucleus and the electron (positron) and neutrino fields. Besides the production of e‾ and υ̃e (or
e and υ⁺ e) particles, 0n1 is changed to 1p1 (or, on the contrary, 1p1 0n1). The intensity of this
interaction is characterised by the weak interaction constant g (coupling constant of the
nucleon and electron-positron fields); g≈1.4 X 10-49 erg-cm3. The probability of beta decay is
characterised by the nuclear matrix element of the transition |Hik| containing: a wave function
of the nucleon in the initial state i; wave functions of the nucleon, electron (positron) and
electron neutrino (anti-neutrino) in the final state k; interaction energy corresponding to the
transition i →k; and, finally, a quantity determining the density of the number of final states
of the system. The selection rules for beta decay establish a considerably higher probability
of allowed transitions and a low probability of so-called forbidden beta transitions (Detlafand
I︠A︡vorskiı̆, 1980).
Of essential significance in the study of beta decay is the analysis of the energy spectrum
N(E) , where N is the number of emitted electrons (or positrons). According to their N(E)
distribution curves, beta spectra are divided into allowed (Fermi-Spectra) and forbidden
spectra. Forbidden spectra, in turn are distinguished by their degree of forbiddenness. For
allowed beta spectra, assuming that mass of the neutrino equals zero,
N (E)dE ≅ F ( Z , E ) pE ( E0 −E )
2
dE
where p and E = momentum and energy of the electrons in units of mec and mec2
me= rest mass of the electron
E0= end-point, or maximum, energy of the electrons (or positrons) of the beta spectrum.
The function F(Z,E) takes account of the influence of the nuclear field on the shape of the
N(E) curve. For forbidden beta spectra, N(E) contains a factor which depends on E0, E and
the degree of forbiddenness.
To decide whether a given beta spectrum belongs to the Fermi or forbidden kind, a Fermi-
Curie plot is made. Thus
to the different distributions of energy between the electron (positron) and the electron
antineutrino (neutrino), the total energy of the two particles being equal to E0 (Detlafand
I︠A︡vorskiı̆, 1980).
According to the current concept, the electron (positron) and the electron antineutrino
(neutrino) do not exist in atomic nuclei but are formed at the instant of emission from the
nucleus as a result of weak interaction between the nucleons in the nucleus. Since new
particles are produced in the beta decay, the methods of non-relativistic quantum mechanics
are inapplicable to this process and the problem is dealt with the methods of quantum field
theory.
In the theory of beta decay, the production of an electron and an electron neutrino (positron
and electron neutrino) is treated as the result of the interaction between a nucleon of the
nucleus and the electron (positron) and neutrino fields. Besides the production of e‾ and υ̃e (or
e and υ⁺ e) particles, 0n1 is changed to 1p1 (or, on the contrary, 1p1 0n1). The intensity of this
interaction is characterised by the weak interaction constant g (coupling constant of the
nucleon and electron-positron fields); g≈1.4 X 10-49 erg-cm3. The probability of beta decay is
characterised by the nuclear matrix element of the transition |Hik| containing: a wave function
of the nucleon in the initial state i; wave functions of the nucleon, electron (positron) and
electron neutrino (anti-neutrino) in the final state k; interaction energy corresponding to the
transition i →k; and, finally, a quantity determining the density of the number of final states
of the system. The selection rules for beta decay establish a considerably higher probability
of allowed transitions and a low probability of so-called forbidden beta transitions (Detlafand
I︠A︡vorskiı̆, 1980).
Of essential significance in the study of beta decay is the analysis of the energy spectrum
N(E) , where N is the number of emitted electrons (or positrons). According to their N(E)
distribution curves, beta spectra are divided into allowed (Fermi-Spectra) and forbidden
spectra. Forbidden spectra, in turn are distinguished by their degree of forbiddenness. For
allowed beta spectra, assuming that mass of the neutrino equals zero,
N (E)dE ≅ F ( Z , E ) pE ( E0 −E )
2
dE
where p and E = momentum and energy of the electrons in units of mec and mec2
me= rest mass of the electron
E0= end-point, or maximum, energy of the electrons (or positrons) of the beta spectrum.
The function F(Z,E) takes account of the influence of the nuclear field on the shape of the
N(E) curve. For forbidden beta spectra, N(E) contains a factor which depends on E0, E and
the degree of forbiddenness.
To decide whether a given beta spectrum belongs to the Fermi or forbidden kind, a Fermi-
Curie plot is made. Thus

K ( E )= [ N exp ( E )
pEF ( Z , E ) ]2
,
Where Nexp(E) is the observed curve of the beta spectrum. For the Fermi beta spectrum, K(E)
is a straight line which intersects the axis of abscissas at E=E0. Deviation of K(E) from a
straight line indicates that the given beta spectrum is of the forbidden kind.
Decay Constant
The decay constant λ for beta decay is
λ = C ∫
0
E
N ( E ) dE = CF (Z,E0)
λ=C∫
0
E
N ( E ) dE=CF(Z , E ₀)
The factor C is determined in the theory of beta decay as
C=
( g2 m ₑ5 c4
2 π h7 )| Hik|
2
Where g=weak interaction constant (coupling constant)
|Hik|=nuclear matrix element
Since λ=ln 2/T1/2, where T1/2 is the half-life, then
F ( Z , E0 ) T 1
2
=T 1
2 red =
2 π3 ℏ7
g2 m ₑ5 c4 ( ln 2 )
Hik ϑ2
The product F(Z,E0)T1/2=T0.5red is called the reduced half-life.
It depends only on the character of the interaction between the nucleons of the nucleus and
the electron-neutrino field. Reduced half-life values, obtained from experimental data, enable
|Hik| to be determined.
According to their T0.5 red values, the types of beta decay can be classified as follows:
(a) Those with log T0.5 red ≈3.5 are superallowed transitions; they include: beta decay of
the neutron, 1H3, and transitions between mirror nuclei [(N-Z=1 for the initial nucleus
and N-Z=-1 for the final one), as well as transitions for which N-Z=±1 for one isobar
and N-Z=±2 for the other (where N is the number of neutrons in the nucleus)]; for
superallowed transitions, the | Hik | values are near to the maximum values;
(b) Those with logT0.5red≈5 are normally allowed transitions, and
pEF ( Z , E ) ]2
,
Where Nexp(E) is the observed curve of the beta spectrum. For the Fermi beta spectrum, K(E)
is a straight line which intersects the axis of abscissas at E=E0. Deviation of K(E) from a
straight line indicates that the given beta spectrum is of the forbidden kind.
Decay Constant
The decay constant λ for beta decay is
λ = C ∫
0
E
N ( E ) dE = CF (Z,E0)
λ=C∫
0
E
N ( E ) dE=CF(Z , E ₀)
The factor C is determined in the theory of beta decay as
C=
( g2 m ₑ5 c4
2 π h7 )| Hik|
2
Where g=weak interaction constant (coupling constant)
|Hik|=nuclear matrix element
Since λ=ln 2/T1/2, where T1/2 is the half-life, then
F ( Z , E0 ) T 1
2
=T 1
2 red =
2 π3 ℏ7
g2 m ₑ5 c4 ( ln 2 )
Hik ϑ2
The product F(Z,E0)T1/2=T0.5red is called the reduced half-life.
It depends only on the character of the interaction between the nucleons of the nucleus and
the electron-neutrino field. Reduced half-life values, obtained from experimental data, enable
|Hik| to be determined.
According to their T0.5 red values, the types of beta decay can be classified as follows:
(a) Those with log T0.5 red ≈3.5 are superallowed transitions; they include: beta decay of
the neutron, 1H3, and transitions between mirror nuclei [(N-Z=1 for the initial nucleus
and N-Z=-1 for the final one), as well as transitions for which N-Z=±1 for one isobar
and N-Z=±2 for the other (where N is the number of neutrons in the nucleus)]; for
superallowed transitions, the | Hik | values are near to the maximum values;
(b) Those with logT0.5red≈5 are normally allowed transitions, and

(c) Those with logT1/2red≈9,≈13, ≈18 are forbidden transitions of the 1st , 2nd and 3rd orders
of forbiddenness, respectively. The last cases correspond to a sharp decrease in the
probability of beta decay, due to large changes in the angular momentum of the
nucleus and, frequently, to the change in the parity of its states.
The decay constant λE for an allowed electron capture is
λE = g ² mₑ ⁵ c ⁴
2 Π ³ℏ ⁷ |Hki|² FE(ε0,Z)
λ= g2 m ₑ5 c4
2 π 3 ℏ7 |Hik |
2
F ₑ(ε0 , Z)
where FE(ε0,Z)=2Π ( 2 ΠZe ²
hc )³ [ε0 + 1 - 1
2 ( 2 ΠZe ²
hc )²]²
F E ( ε0 , Z )=2 Π ( 2 ΠZ e2
hc )3
[ε 0+1−1
2 ( 2 ΠZ e2
hc )2
]2
, ε0 = E ₀
mₑc ² .
This formula does not take into account the relativistic effects which become appreciable
when the value of E0 approaches the rest energy of the electron, equal to 0.511MeV.
The state of the quantum system is said to be even if the corresponding wave function is not
reversed in sign when the signs of all the coordinates of the particles in the system are
changed (in inversions); otherwise it is said to be odd. The conservation of the sign of the
wave function upon a space inversion can also be characterised by even parity P (where P =
+1). If, upon changing the signs of the coordinates of the wave function, the sign of the latter
is reversed, then the parity is said to be odd (P=-1). The conception of the parity of state and
of the wave function is related to the symmetry of space, i.e. to the equivalence in space of
the right- and left-hand directions, upward and downward, etc.
Any system of particles can be in a state with a definite parity if the number of particles in it
remains constant or is changed by an even number.
It follows from the properties of the Schrödinger equation that if the energy of a particle (or
system of particles) is conserved constant, then its parity is also conserved (parity
conservation law). A system of particles before and after beta decay should correspond to
wave functions of the same parity [nucleus before decay; nucleus, beta particle and (anti-
neutrino) neutrino after decay].
It has been established that in weak interactions which, in particular, bring about beta decay,
the parity of the wave function of the system can change in decay (non-conservation of
parity). Along with the state described, for instance, by an even function, an odd state can
of forbiddenness, respectively. The last cases correspond to a sharp decrease in the
probability of beta decay, due to large changes in the angular momentum of the
nucleus and, frequently, to the change in the parity of its states.
The decay constant λE for an allowed electron capture is
λE = g ² mₑ ⁵ c ⁴
2 Π ³ℏ ⁷ |Hki|² FE(ε0,Z)
λ= g2 m ₑ5 c4
2 π 3 ℏ7 |Hik |
2
F ₑ(ε0 , Z)
where FE(ε0,Z)=2Π ( 2 ΠZe ²
hc )³ [ε0 + 1 - 1
2 ( 2 ΠZe ²
hc )²]²
F E ( ε0 , Z )=2 Π ( 2 ΠZ e2
hc )3
[ε 0+1−1
2 ( 2 ΠZ e2
hc )2
]2
, ε0 = E ₀
mₑc ² .
This formula does not take into account the relativistic effects which become appreciable
when the value of E0 approaches the rest energy of the electron, equal to 0.511MeV.
The state of the quantum system is said to be even if the corresponding wave function is not
reversed in sign when the signs of all the coordinates of the particles in the system are
changed (in inversions); otherwise it is said to be odd. The conservation of the sign of the
wave function upon a space inversion can also be characterised by even parity P (where P =
+1). If, upon changing the signs of the coordinates of the wave function, the sign of the latter
is reversed, then the parity is said to be odd (P=-1). The conception of the parity of state and
of the wave function is related to the symmetry of space, i.e. to the equivalence in space of
the right- and left-hand directions, upward and downward, etc.
Any system of particles can be in a state with a definite parity if the number of particles in it
remains constant or is changed by an even number.
It follows from the properties of the Schrödinger equation that if the energy of a particle (or
system of particles) is conserved constant, then its parity is also conserved (parity
conservation law). A system of particles before and after beta decay should correspond to
wave functions of the same parity [nucleus before decay; nucleus, beta particle and (anti-
neutrino) neutrino after decay].
It has been established that in weak interactions which, in particular, bring about beta decay,
the parity of the wave function of the system can change in decay (non-conservation of
parity). Along with the state described, for instance, by an even function, an odd state can
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

also appear. This phenomenon was first discovered in the beta decay of K mesons. In
essence, this is the decay of a K meson into two or even three pi mesons. In beta decay, the
violation of parity conservation is manifested in the asymmetry of the spatial directions of the
electrons emitted by the nuclei: fewer electrons are emitted in the direction of spin of the
nuclei than in the opposite direction. It follows from this asymmetry that there is a definite
relationship between the direction of spin of the particle and the direction of its motion in
space. The spins of a neutrino and antineutrino should always be oriented parallel or
antiparallel to the direction of their motion: the antineutrino is oriented along the direction of
motion and the neutrino in the opposite direction (longitudinal polarization). If spin is likened
to rotation, then the motion of the antineutrino corresponds to the motion of right-hand spin
and that of the neutrino to left-hand spin. Accordingly distinction is made between right-hand
helicity of the antineutrino and left-hand helicity of the neutrino.
Maximum research results were established from the evidences found from experiments in which
the radiation from radioactive compounds was allowed to pass through magnetic or electric fields.
While performing such an experiment it was found that the gamma rays passed through the fields
without any deflection. But unfortunately, the alpha and beta rays deflected to opposite directions.
Thus it proves that alpha and beta are charged while the gamma ray is not.
Shielding
While shooting from a gun, a bullet penetrates depending on the
composition of the material of the bullet used and the composition of the
material of the target. For example, a pellet from an air gun will be
stopped by a few millimetres of wood, whereas a bullet from a high
powered rifle will pass through many millimeters of steel. We may say it is
the similar in case of ionizing radiation. Different ionizing radiations have
different penetrating ability (α-, β- or γ-radiation). The examples below
give such an idea about the penetration of the radiation from the
radioactive sources.
Alpha particles which come from radioactive sources have a range of less than
10 cm in air. In condensed matter medium (e.g. water or tissue) the range becomes even
shorter (the difference in range is approximately 1/1000, due to the difference in density) –
almost less than 100 mm. Logically, it can be understood that α -particles will not be able to
penetrate even clothing. We can sit on a radioactive source and will not cause any harm to
ourselves if it were only the α –particles that were emitted . But if the source happens to be
inside our body, all the energy is deposited in the body and may give a large radiation dose.
Aleksandr Litvinenko in 2006 with Po-210 of such an incident. Po-210 emit an alpha particle
with energy 5.3 MeV.
Beta-particles have an energy of 1 MeV and its range is about 5 mm in soft tissue. Almost
all the β-particles have an energy less than 1 MeV. And hence all the β-particles coming
from environmental sources, are stopped by our clothing.
Gamma-radiation can penetrate tissue in our body and can even concrete in it. We have,
50% of the γ-rays from Cs-137, having an energy of 0.662 MeV and can penetrate a water
essence, this is the decay of a K meson into two or even three pi mesons. In beta decay, the
violation of parity conservation is manifested in the asymmetry of the spatial directions of the
electrons emitted by the nuclei: fewer electrons are emitted in the direction of spin of the
nuclei than in the opposite direction. It follows from this asymmetry that there is a definite
relationship between the direction of spin of the particle and the direction of its motion in
space. The spins of a neutrino and antineutrino should always be oriented parallel or
antiparallel to the direction of their motion: the antineutrino is oriented along the direction of
motion and the neutrino in the opposite direction (longitudinal polarization). If spin is likened
to rotation, then the motion of the antineutrino corresponds to the motion of right-hand spin
and that of the neutrino to left-hand spin. Accordingly distinction is made between right-hand
helicity of the antineutrino and left-hand helicity of the neutrino.
Maximum research results were established from the evidences found from experiments in which
the radiation from radioactive compounds was allowed to pass through magnetic or electric fields.
While performing such an experiment it was found that the gamma rays passed through the fields
without any deflection. But unfortunately, the alpha and beta rays deflected to opposite directions.
Thus it proves that alpha and beta are charged while the gamma ray is not.
Shielding
While shooting from a gun, a bullet penetrates depending on the
composition of the material of the bullet used and the composition of the
material of the target. For example, a pellet from an air gun will be
stopped by a few millimetres of wood, whereas a bullet from a high
powered rifle will pass through many millimeters of steel. We may say it is
the similar in case of ionizing radiation. Different ionizing radiations have
different penetrating ability (α-, β- or γ-radiation). The examples below
give such an idea about the penetration of the radiation from the
radioactive sources.
Alpha particles which come from radioactive sources have a range of less than
10 cm in air. In condensed matter medium (e.g. water or tissue) the range becomes even
shorter (the difference in range is approximately 1/1000, due to the difference in density) –
almost less than 100 mm. Logically, it can be understood that α -particles will not be able to
penetrate even clothing. We can sit on a radioactive source and will not cause any harm to
ourselves if it were only the α –particles that were emitted . But if the source happens to be
inside our body, all the energy is deposited in the body and may give a large radiation dose.
Aleksandr Litvinenko in 2006 with Po-210 of such an incident. Po-210 emit an alpha particle
with energy 5.3 MeV.
Beta-particles have an energy of 1 MeV and its range is about 5 mm in soft tissue. Almost
all the β-particles have an energy less than 1 MeV. And hence all the β-particles coming
from environmental sources, are stopped by our clothing.
Gamma-radiation can penetrate tissue in our body and can even concrete in it. We have,
50% of the γ-rays from Cs-137, having an energy of 0.662 MeV and can penetrate a water

layer of about 9 cm., known as half-value layer. Fortunately γ-radiation can be easily
measured, be the source be outside or inside the body. Moreover, isotopes emitting γ-
radiation can be used as medical diagnostic.
The binding energy of a nucleus determines which, if any, of these three decay processes is
energetically possible. For example, in the decay of the 60Co27 nucleus into the 60Ni28 nucleus,
a β‾-particle is emitted, i.e.,
60Co27→ 60Ni28 + e‾ + ῡ e ,
releasing an energy of 1.56 MeV in the form of kinetic energies of the three products. An
example of the β - particle emission in the decay of⁺ 22Na11, i.e.,
22Na11→22Ne10 + e +υ⁺ e +0.55 MeV.
Further, an example of electron capture is the decay of the 37Ar18 nucleus into the 37Cl17
nucleus after an atomic electron is absorbed, i.e.,
37Ar18 + e¯→37Cl17 + υe.
The energy released in this reaction is 0.0186 MeV.
A nucleus lying above the region of stability, i.e. , region of neuron excess,
becomes stable by reducing the number of neurons in it. In other words, such a nucleus
disintegrates in a manner that its N/Z ratio gets reduced. This is achieved through the β‾-
decay where a neuron inside the nucleus changes into a proton, simultaneously creating and
emitting an electron and a neutrino.
Similarly, a nucleus lying below the stability region becomes stable by increasing its N/Z
ratio. Thus, such a nucleus decays by emitting a β - particle or by electron capture. In the β -⁺ ⁺
decay, a proton inside the nucleus changes into a neutron, simultaneously creating and
ejecting a positron and an antineutrino. In electron capture, an atomic orbital electron of a
nucleus combines with a proton of the nucleus to change the proton into a neutron and a
neutrino(Mani and Mehta, 1990).
To study the energetics of the beta-decay process, we write the mass-energy equations for
this process in terms of the atomic masses:
AMZ = AMZ+1 + Q/c2 (β¯- decay), (1)
measured, be the source be outside or inside the body. Moreover, isotopes emitting γ-
radiation can be used as medical diagnostic.
The binding energy of a nucleus determines which, if any, of these three decay processes is
energetically possible. For example, in the decay of the 60Co27 nucleus into the 60Ni28 nucleus,
a β‾-particle is emitted, i.e.,
60Co27→ 60Ni28 + e‾ + ῡ e ,
releasing an energy of 1.56 MeV in the form of kinetic energies of the three products. An
example of the β - particle emission in the decay of⁺ 22Na11, i.e.,
22Na11→22Ne10 + e +υ⁺ e +0.55 MeV.
Further, an example of electron capture is the decay of the 37Ar18 nucleus into the 37Cl17
nucleus after an atomic electron is absorbed, i.e.,
37Ar18 + e¯→37Cl17 + υe.
The energy released in this reaction is 0.0186 MeV.
A nucleus lying above the region of stability, i.e. , region of neuron excess,
becomes stable by reducing the number of neurons in it. In other words, such a nucleus
disintegrates in a manner that its N/Z ratio gets reduced. This is achieved through the β‾-
decay where a neuron inside the nucleus changes into a proton, simultaneously creating and
emitting an electron and a neutrino.
Similarly, a nucleus lying below the stability region becomes stable by increasing its N/Z
ratio. Thus, such a nucleus decays by emitting a β - particle or by electron capture. In the β -⁺ ⁺
decay, a proton inside the nucleus changes into a neutron, simultaneously creating and
ejecting a positron and an antineutrino. In electron capture, an atomic orbital electron of a
nucleus combines with a proton of the nucleus to change the proton into a neutron and a
neutrino(Mani and Mehta, 1990).
To study the energetics of the beta-decay process, we write the mass-energy equations for
this process in terms of the atomic masses:
AMZ = AMZ+1 + Q/c2 (β¯- decay), (1)

AMZ = AMZ-1 +2me+ Q/c2 (β - decay), (2)⁺
AMZ = AM*Z-1 + Q/c2 (electron capture). (3)
In these equations, the neutrino mass does not appear because, a neutrino (and also an
antineutrino) is massless. Further, Q is the energy available in the decay. As can be noted, the
electron mass does not appear on the right-hand side of (1). His is because an electron is
needed for the atom AMZ+1 to become neutral. On the right-hand side of the β - decay⁺
equation, there are two electron masses. Of these, one is due to the positron the nucleus emits
and the other is due to the extra electron (in the atom AMZ-1) the atom releases to make itself
neutral. In electron capture eq (3), an orbital electron is captured by the nucleus, and thus the
atom AMZ-1 produced is neutral but in an excited state, indicated by the superscript asterisk
(Mani and Mehta, 1990).
Binding Energy
Let us consider a nucleus containing Z protons and N neutrons. If we attempt to separate this
nucleus into individual protons and neutrons, a certain amount of work has to be done
because these particles are held together by attractive forces. In other words, energy must be
supplied to the nucleus to separate it into its individual constituents and move them to infinity
with each constituent being at rest. This energy necessary to separate all the particles is called
the binding energy of the nucleus. After the separation, if the nucleons interact and coalesce
to form a nucleus, their energy must be less than what it was when they were separated.
According to the Einstein mass energy relation, their combined mass in the coalesced state
must be less than the sum of their masses when they are far away from one another. If we
denote the loss in mass by Δmc2 which is the binding energy, i.e., the binding energy (BE) is
BE = Δmc2.
If M, Mn, and Mp are the masses of a nucleus (AXZ), a neutron, a proton, respectively, then the
mass defect Δm is
Δm= NMn + ZMp – M
And the binding energy of the nucleus is
BE =(NMn + ZMp – M)c2.
The energy of the state of infinite separation of nucleons at rest is taken to be zero.
It is more convenient to work with the mass of an atom than with that of the nucleus. To do
this, we add to and subtract from the above equation the mass of Z electrons. Thus,
BE=(NMn + ZMp + ZMe-M – ZMe)c2.
Now, ZMp + ZMe= Z(Mp+ Me). The quantity (Mp+ Me) is just the mass of one atom of
hydrogen (MH) since the binding energy of an electron is negligible as compared to (Mp+
Me)c2. Similarly, (M(AXZ)+ ZMe) is the mass of the atom AXZ (MA). Thus, the binding energy
in terms of the atomic masses is
BE=(NMn+ ZMH-MA)c2.
The binding energy and mass defect are not peculiar to a nucleus. An electron in an atom, an
atom in a molecule, and a molecule in a crystal each has a binding energy, but it is usually so
small that its mass equivalent can be neglected. The mass equivalent of the binding energy of
AMZ = AM*Z-1 + Q/c2 (electron capture). (3)
In these equations, the neutrino mass does not appear because, a neutrino (and also an
antineutrino) is massless. Further, Q is the energy available in the decay. As can be noted, the
electron mass does not appear on the right-hand side of (1). His is because an electron is
needed for the atom AMZ+1 to become neutral. On the right-hand side of the β - decay⁺
equation, there are two electron masses. Of these, one is due to the positron the nucleus emits
and the other is due to the extra electron (in the atom AMZ-1) the atom releases to make itself
neutral. In electron capture eq (3), an orbital electron is captured by the nucleus, and thus the
atom AMZ-1 produced is neutral but in an excited state, indicated by the superscript asterisk
(Mani and Mehta, 1990).
Binding Energy
Let us consider a nucleus containing Z protons and N neutrons. If we attempt to separate this
nucleus into individual protons and neutrons, a certain amount of work has to be done
because these particles are held together by attractive forces. In other words, energy must be
supplied to the nucleus to separate it into its individual constituents and move them to infinity
with each constituent being at rest. This energy necessary to separate all the particles is called
the binding energy of the nucleus. After the separation, if the nucleons interact and coalesce
to form a nucleus, their energy must be less than what it was when they were separated.
According to the Einstein mass energy relation, their combined mass in the coalesced state
must be less than the sum of their masses when they are far away from one another. If we
denote the loss in mass by Δmc2 which is the binding energy, i.e., the binding energy (BE) is
BE = Δmc2.
If M, Mn, and Mp are the masses of a nucleus (AXZ), a neutron, a proton, respectively, then the
mass defect Δm is
Δm= NMn + ZMp – M
And the binding energy of the nucleus is
BE =(NMn + ZMp – M)c2.
The energy of the state of infinite separation of nucleons at rest is taken to be zero.
It is more convenient to work with the mass of an atom than with that of the nucleus. To do
this, we add to and subtract from the above equation the mass of Z electrons. Thus,
BE=(NMn + ZMp + ZMe-M – ZMe)c2.
Now, ZMp + ZMe= Z(Mp+ Me). The quantity (Mp+ Me) is just the mass of one atom of
hydrogen (MH) since the binding energy of an electron is negligible as compared to (Mp+
Me)c2. Similarly, (M(AXZ)+ ZMe) is the mass of the atom AXZ (MA). Thus, the binding energy
in terms of the atomic masses is
BE=(NMn+ ZMH-MA)c2.
The binding energy and mass defect are not peculiar to a nucleus. An electron in an atom, an
atom in a molecule, and a molecule in a crystal each has a binding energy, but it is usually so
small that its mass equivalent can be neglected. The mass equivalent of the binding energy of
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
a nucleus is not negligible in comparison to the total mass of the nucleus because the nuclear
forces are very strong.
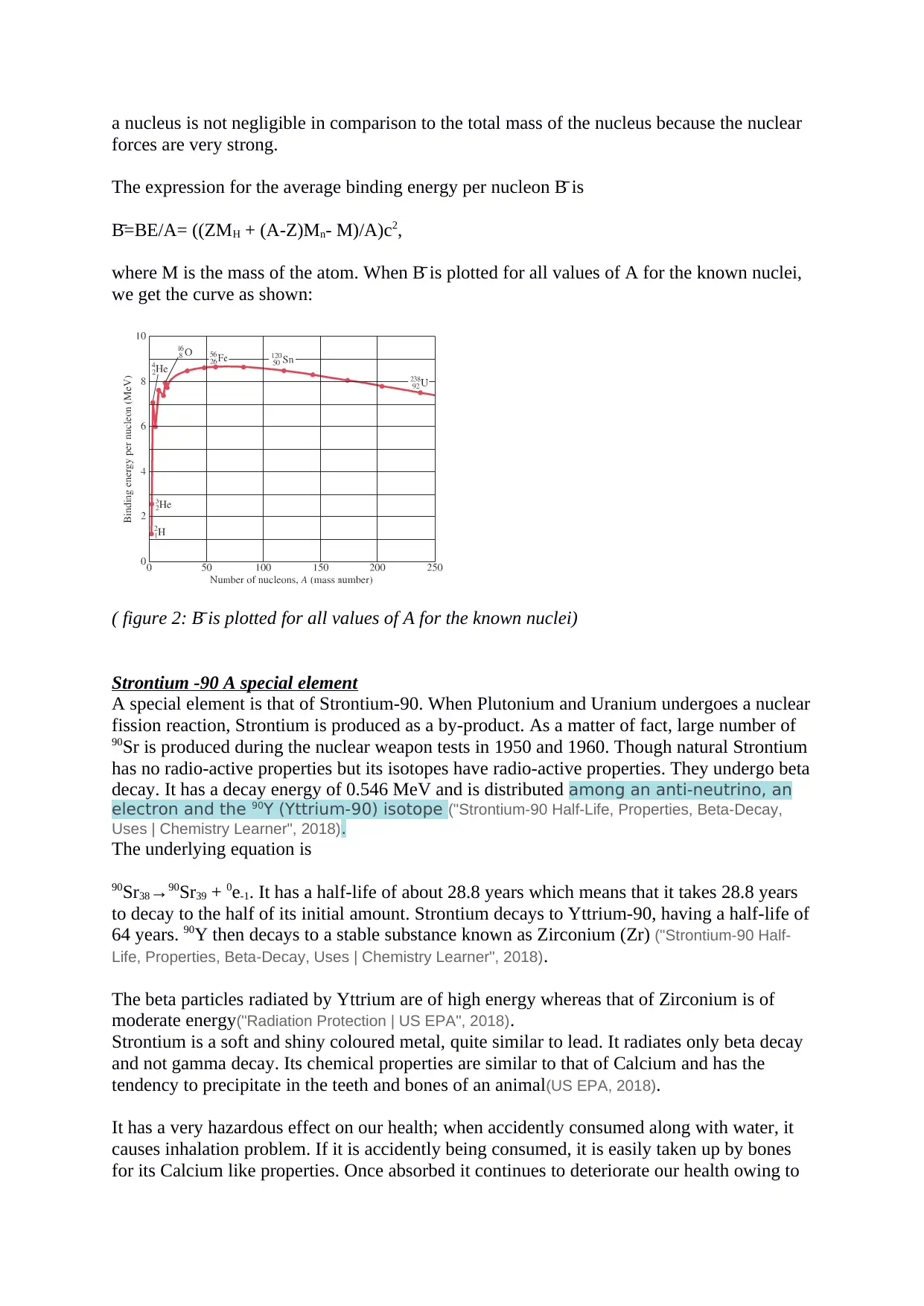
The expression for the average binding energy per nucleon B̄ is
B̄=BE/A= ((ZMH + (A-Z)Mn- M)/A)c2,
where M is the mass of the atom. When B̄ is plotted for all values of A for the known nuclei,
we get the curve as shown:
( figure 2: B̄ is plotted for all values of A for the known nuclei)
Strontium -90 A special element
A special element is that of Strontium-90. When Plutonium and Uranium undergoes a nuclear
fission reaction, Strontium is produced as a by-product. As a matter of fact, large number of
90Sr is produced during the nuclear weapon tests in 1950 and 1960. Though natural Strontium
has no radio-active properties but its isotopes have radio-active properties. They undergo beta
decay. It has a decay energy of 0.546 MeV and is distributed among an anti-neutrino, an
electron and the 90Y (Yttrium-90) isotope ("Strontium-90 Half-Life, Properties, Beta-Decay,
Uses | Chemistry Learner", 2018).
The underlying equation is
90Sr38→90Sr39 + 0e-1. It has a half-life of about 28.8 years which means that it takes 28.8 years
to decay to the half of its initial amount. Strontium decays to Yttrium-90, having a half-life of
64 years. 90Y then decays to a stable substance known as Zirconium (Zr) ("Strontium-90 Half-
Life, Properties, Beta-Decay, Uses | Chemistry Learner", 2018).
The beta particles radiated by Yttrium are of high energy whereas that of Zirconium is of
moderate energy("Radiation Protection | US EPA", 2018).
Strontium is a soft and shiny coloured metal, quite similar to lead. It radiates only beta decay
and not gamma decay. Its chemical properties are similar to that of Calcium and has the
tendency to precipitate in the teeth and bones of an animal(US EPA, 2018).
It has a very hazardous effect on our health; when accidently consumed along with water, it
causes inhalation problem. If it is accidently being consumed, it is easily taken up by bones
for its Calcium like properties. Once absorbed it continues to deteriorate our health owing to
forces are very strong.
The expression for the average binding energy per nucleon B̄ is
B̄=BE/A= ((ZMH + (A-Z)Mn- M)/A)c2,
where M is the mass of the atom. When B̄ is plotted for all values of A for the known nuclei,
we get the curve as shown:
( figure 2: B̄ is plotted for all values of A for the known nuclei)
Strontium -90 A special element
A special element is that of Strontium-90. When Plutonium and Uranium undergoes a nuclear
fission reaction, Strontium is produced as a by-product. As a matter of fact, large number of
90Sr is produced during the nuclear weapon tests in 1950 and 1960. Though natural Strontium
has no radio-active properties but its isotopes have radio-active properties. They undergo beta
decay. It has a decay energy of 0.546 MeV and is distributed among an anti-neutrino, an
electron and the 90Y (Yttrium-90) isotope ("Strontium-90 Half-Life, Properties, Beta-Decay,
Uses | Chemistry Learner", 2018).
The underlying equation is
90Sr38→90Sr39 + 0e-1. It has a half-life of about 28.8 years which means that it takes 28.8 years
to decay to the half of its initial amount. Strontium decays to Yttrium-90, having a half-life of
64 years. 90Y then decays to a stable substance known as Zirconium (Zr) ("Strontium-90 Half-
Life, Properties, Beta-Decay, Uses | Chemistry Learner", 2018).
The beta particles radiated by Yttrium are of high energy whereas that of Zirconium is of
moderate energy("Radiation Protection | US EPA", 2018).
Strontium is a soft and shiny coloured metal, quite similar to lead. It radiates only beta decay
and not gamma decay. Its chemical properties are similar to that of Calcium and has the
tendency to precipitate in the teeth and bones of an animal(US EPA, 2018).
It has a very hazardous effect on our health; when accidently consumed along with water, it
causes inhalation problem. If it is accidently being consumed, it is easily taken up by bones
for its Calcium like properties. Once absorbed it continues to deteriorate our health owing to

its long half-life period. It also causes cancer of bones, Leukemia and softening of tissues
around our bone marrow (US EPA, 2018).
References:
Detlaf, A. A. and I︠A︡vorskiı̆, B. M.(1980). Handbook of physics.Translated from the
Russian by Nicholas Weinstein, 3rd ed. London: Mir Publications.p. 1131.
Mani, H. S. and Mehta, G. K.(1990).Introduction to Modern Physics. New Delhi:
Affiliated East West Press PVT Ltd.ISBN 10: 8185095736 / ISBN 13:
9788185095738
Strontium-90 Half-Life, Properties, Beta-Decay, Uses | Chemistry Learner. (2018). Retrieved
from http://www.chemistrylearner.com/strontium-90.html
US EPA. (2018). Radiation Protection | US EPA. [online] Available at:
https://www.epa.gov/radiation [Accessed 24 Jul. 2018].
Radiation Protection | US EPA. (2018). Retrieved from https://www.epa.gov/radiation
around our bone marrow (US EPA, 2018).
References:
Detlaf, A. A. and I︠A︡vorskiı̆, B. M.(1980). Handbook of physics.Translated from the
Russian by Nicholas Weinstein, 3rd ed. London: Mir Publications.p. 1131.
Mani, H. S. and Mehta, G. K.(1990).Introduction to Modern Physics. New Delhi:
Affiliated East West Press PVT Ltd.ISBN 10: 8185095736 / ISBN 13:
9788185095738
Strontium-90 Half-Life, Properties, Beta-Decay, Uses | Chemistry Learner. (2018). Retrieved
from http://www.chemistrylearner.com/strontium-90.html
US EPA. (2018). Radiation Protection | US EPA. [online] Available at:
https://www.epa.gov/radiation [Accessed 24 Jul. 2018].
Radiation Protection | US EPA. (2018). Retrieved from https://www.epa.gov/radiation
1 out of 9
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.
