Biostatistics and Informatics Assignment: Data Analysis and SPSS
VerifiedAdded on 2023/06/04
|10
|1445
|78
Homework Assignment
AI Summary
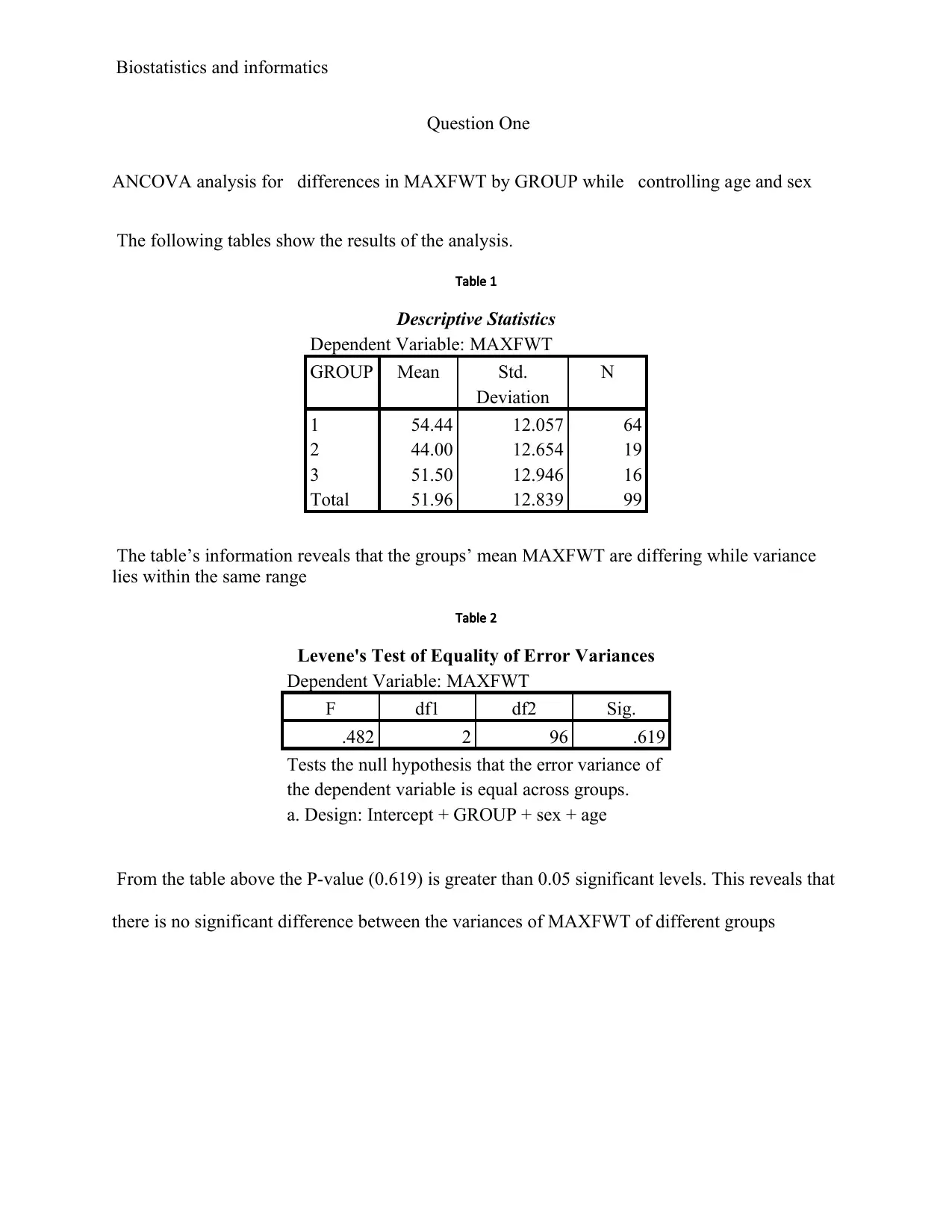
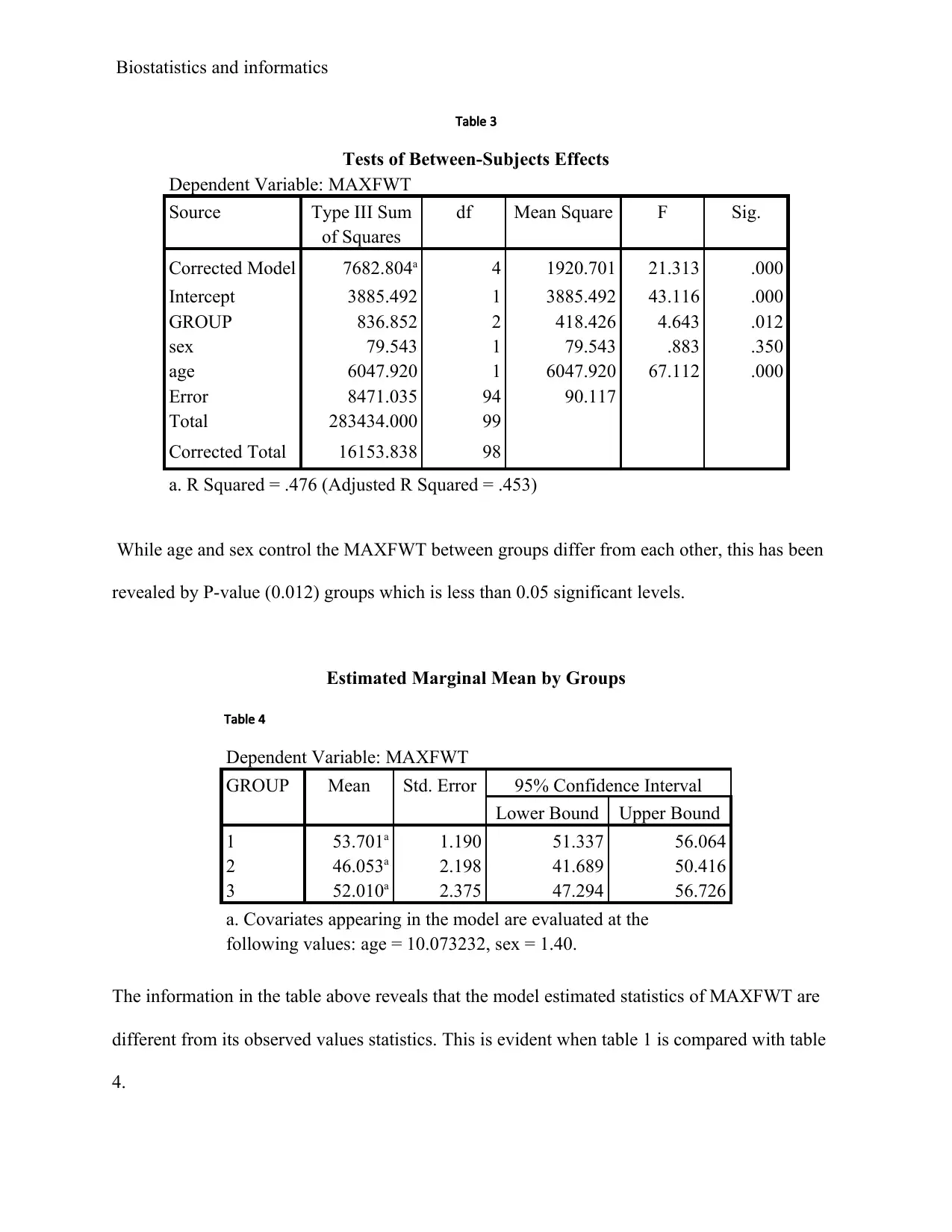
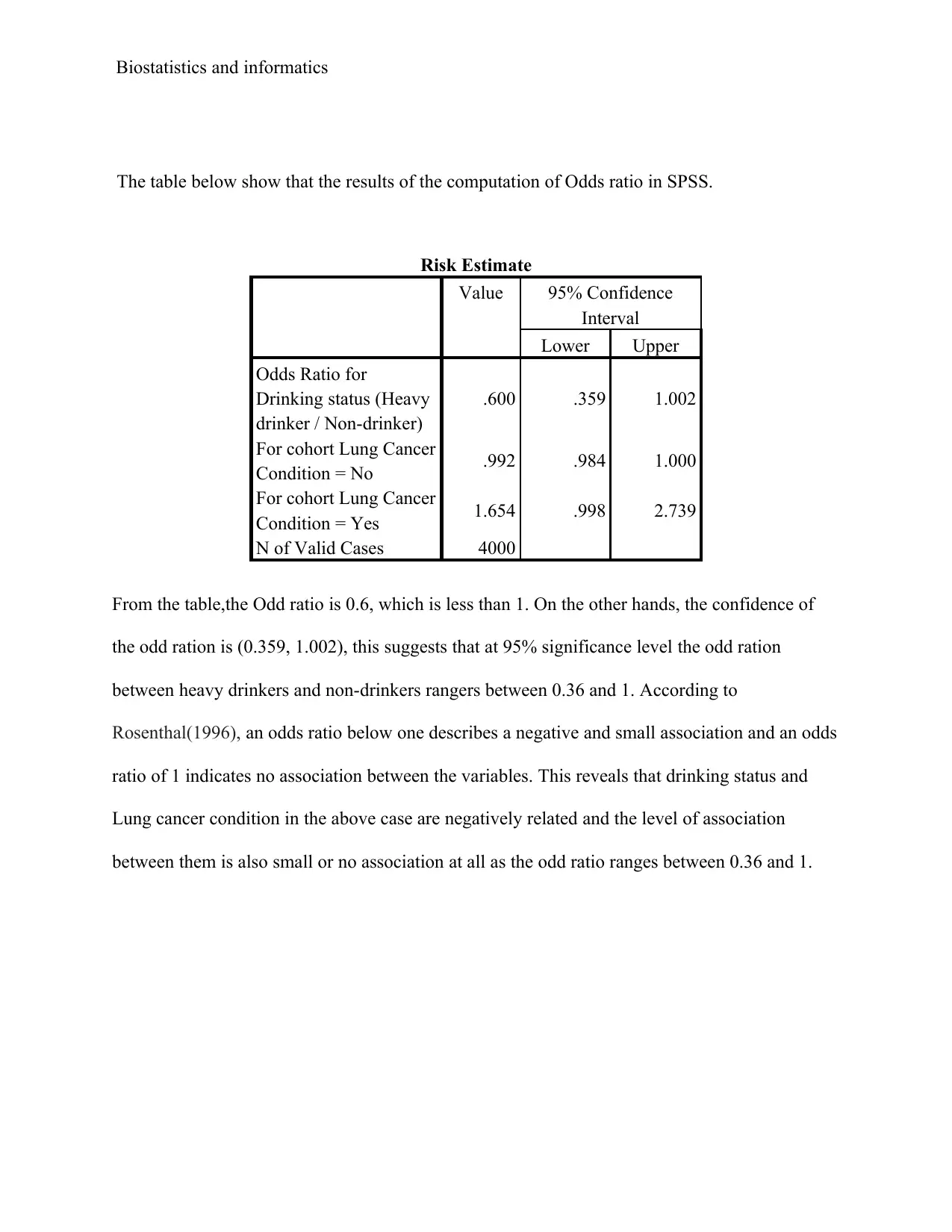
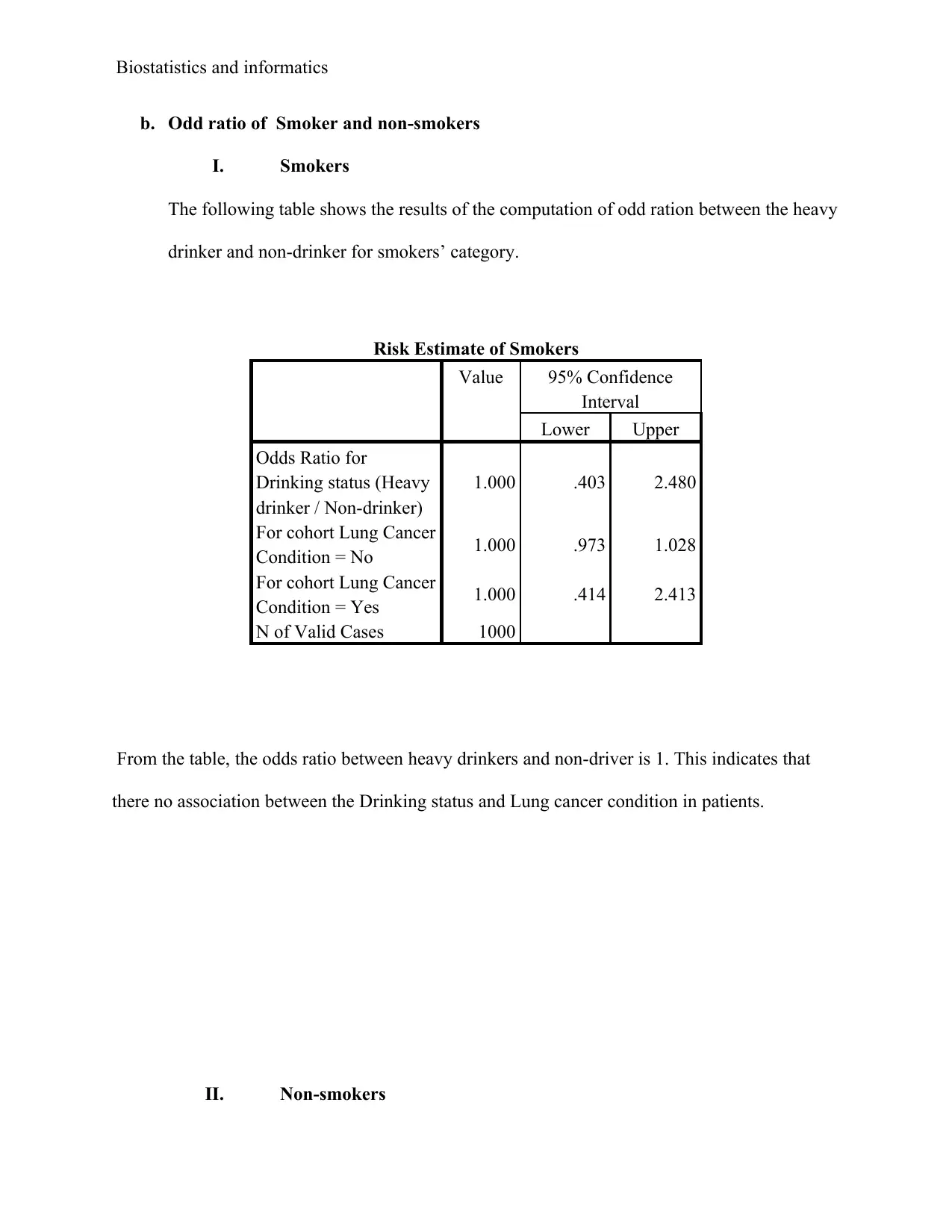
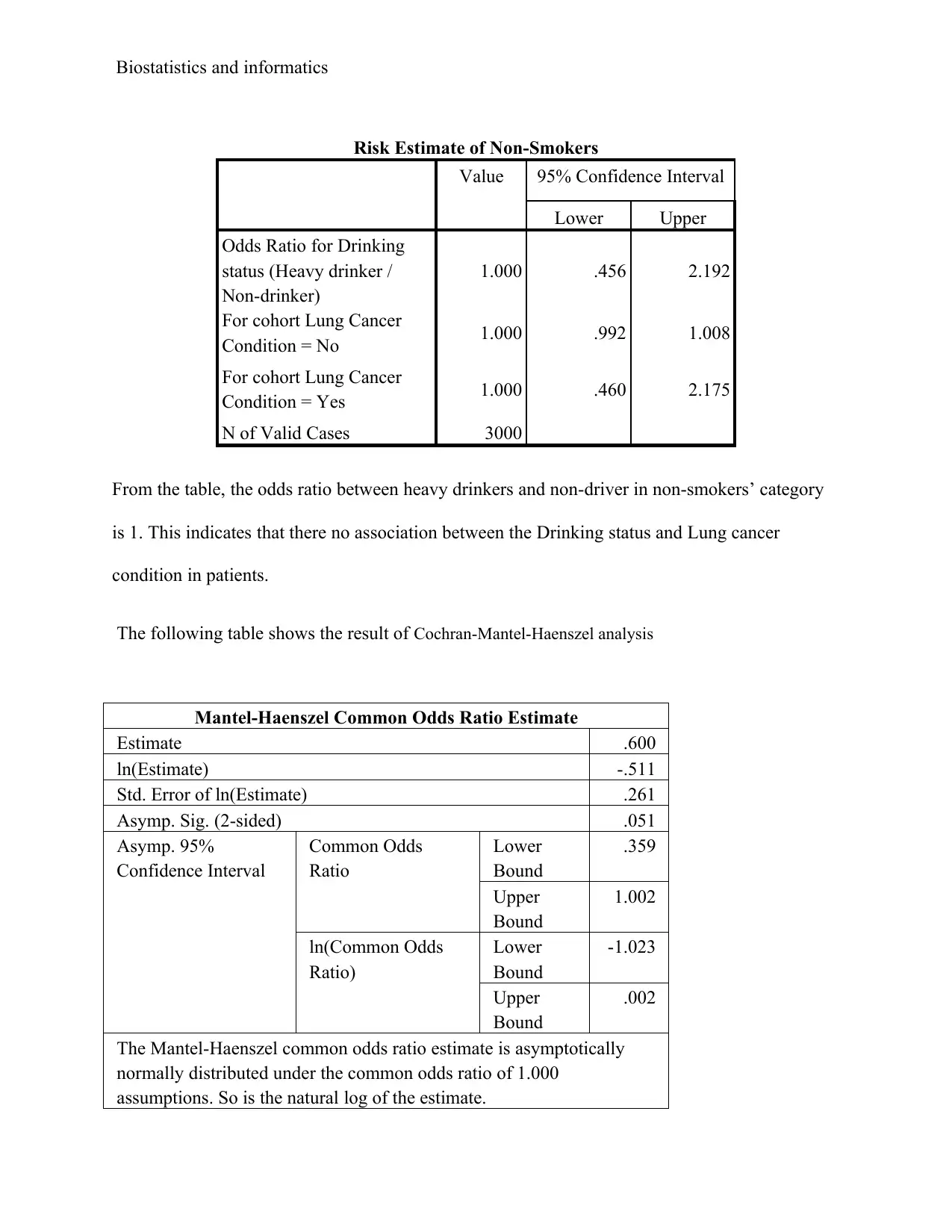
This document provides a comprehensive solution to a biostatistics assignment. The assignment involves analyzing data using SPSS to address two primary research questions. The first question focuses on examining the differences in MAXFWT (a measure of neurological function) across different exposure groups (GROUP), while controlling for age and sex using ANCOVA. The analysis includes descriptive statistics, Levene's test, tests of between-subjects effects, and estimated marginal means. The second question explores the association between OC-use and MI (myocardial infarction) using odds ratios, providing statistical evidence for the relationship and describing the size of the effect. Furthermore, the analysis extends to assess the association between drinking status and lung cancer, considering smokers and non-smokers separately, and employing the Cochran-Mantel-Haenszel test to determine the statistical significance of the findings. The document includes detailed tables, interpretations of the results, and relevant references.
1 out of 10











![[object Object]](/_next/static/media/star-bottom.7253800d.svg)