Biostatistics: Measures of Association, Proportion, Hypothesis Testing, and Significance Testing

This paper examines a number of crucial areas of biostatistics. These areas include hypothesis testing, measures of association and significance testing. These areas are examined through a series of questions. The three questions each covers one of the areas highlighted above. The first question covers measures of association, question two covers proportion and hypothesis testing and the third question covers significance testing. The paper answers these questions and gives a brief description of each area.

RUNNING HEADER: BIOSTATISTICS 1
BIOSTATISTICS
Students Name
Institutional affiliation

BIOSTATISTICS 2
Biostatistics
Introduction
Biostatistics is the application of statistical methods to biological sciences. This paper
examines a number of crucial areas of biostatistics. These areas include hypothesis testing,
measures of association and significance testing. These areas are examined through a series of
questions. The three questions each covers one of the areas highlighted above. The first question
covers measures of association, question two covers proportion and hypothesis testing and the
third question covers significance testing. The paper answers these questions and gives a brief
description of each area.
Measures of association
Measures of association are used to quantify the relationship between two or more
variables. (Dicker, Coronado & Koo, 2006). Several methods of analysis can be used to
determine measures of associations. These include correlation analysis and regression analysis
(Gaddis, 1990). Examples of such methods of analysis include Pearson’s correlation coefficient,
Spearman order correlation coefficient, chi-square test, relative and odd ratio (Haung, 2016). To
determine the association between alcohol and nicotine consumption we shall carry out a chi-
square test on the data provided. A chi-square test is a measure of significance rather than a
measure of the strength of the association.

BIOSTATISTICS 3
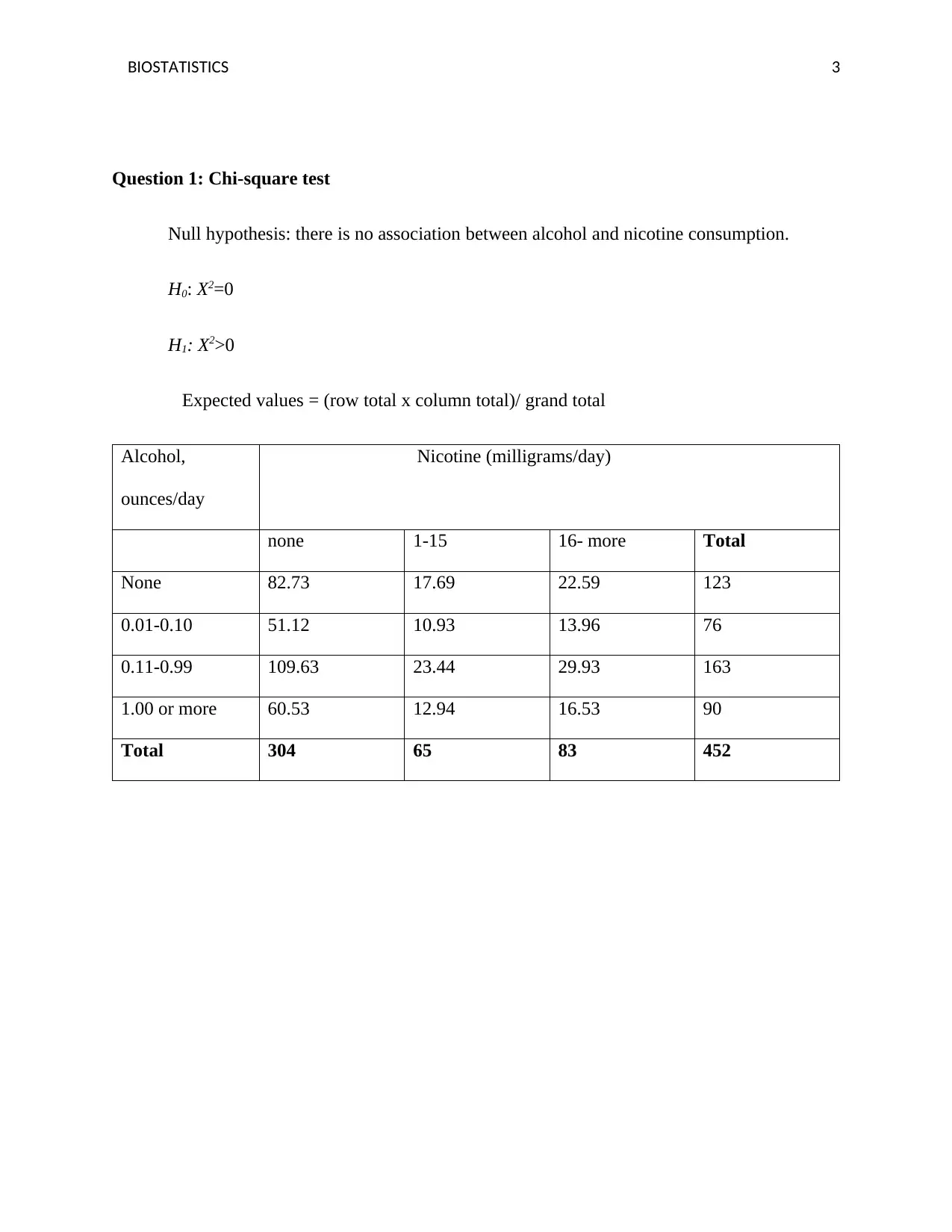
Question 1: Chi-square test
Null hypothesis: there is no association between alcohol and nicotine consumption.
H0: X2=0
H1: X2>0
Expected values = (row total x column total)/ grand total
Alcohol,
ounces/day
Nicotine (milligrams/day)
none 1-15 16- more Total
None 82.73 17.69 22.59 123
0.01-0.10 51.12 10.93 13.96 76
0.11-0.99 109.63 23.44 29.93 163
1.00 or more 60.53 12.94 16.53 90
Total 304 65 83 452

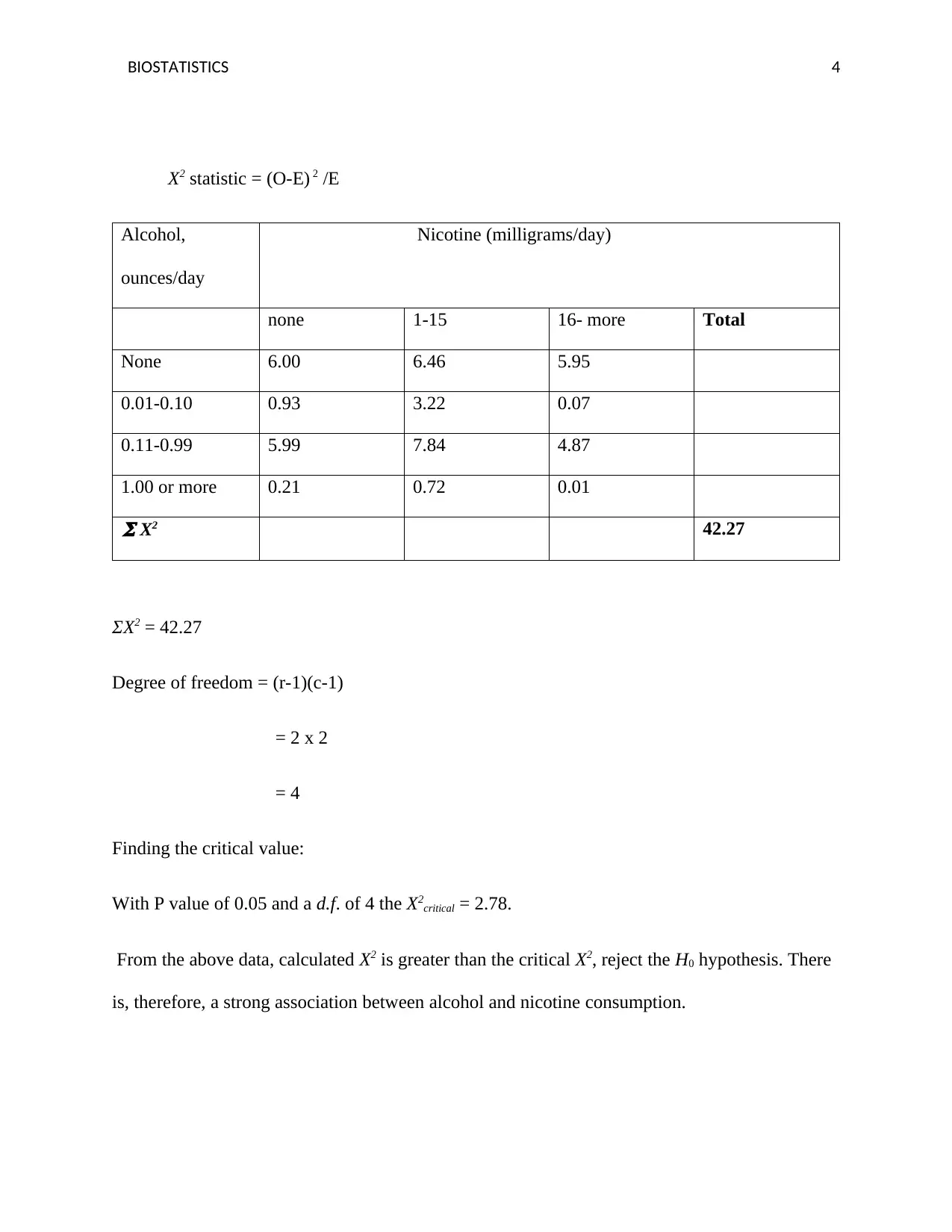
BIOSTATISTICS 4
X2 statistic = (O-E) 2 /E
Alcohol,
ounces/day
Nicotine (milligrams/day)
none 1-15 16- more Total
None 6.00 6.46 5.95
0.01-0.10 0.93 3.22 0.07
0.11-0.99 5.99 7.84 4.87
1.00 or more 0.21 0.72 0.01
𝚺 X2 42.27
ΣX2 = 42.27
Degree of freedom = (r-1)(c-1)
= 2 x 2
= 4
Finding the critical value:
With P value of 0.05 and a d.f. of 4 the X2critical = 2.78.
From the above data, calculated X2 is greater than the critical X2, reject the H0 hypothesis. There
is, therefore, a strong association between alcohol and nicotine consumption.

BIOSTATISTICS 5
The strength of the association
Most measures of association have a scale such that they reach a value of 1 if the two
variables have a perfect association with each other (Daniel, 2009). Methods used to measure the
magnitude of association include Cramer’s V, Lambda, Phi, Kendall’s taub and Kendall’s tauc
(Cohen J, 2010). Chi-square does not show the strength of the association between the variables.
Question 2: Proportion and hypothesis testing
Proportion is the comparison of a part, a number or share in relation to the whole. It is a
type of a ratio in which the numerator is part of the denominator. (Dicker, Coronado & Koo
2006). Proportion can be expressed as a decimal, fraction or a percentage.
Proportion is calculated by Proportion= number of events of a particular characteristics
total number of events ∈which thenumerator is a⊂¿ ¿
p= the number with chracteritic of interest
sample ¿ ¿ ¿
Question 2 a.
I. The proportion of the sample that underwent HIV testing: =
those whoundwent HIV testing
total sample ¿ ¿ ¿
= 49
112
= 0.4375

BIOSTATISTICS 6
II. The proportion of those unemployed who underwent HIV testing
unemployed whounderwent HIV testing
total umemployed
= 18
53
=0.3396
III. The proportion of the employed who underwent HIV testing =
employed whounderwent HIV testing
total employed
= 31
59
= 0.5254
IV. To determine whether undergoing HIV testing is associated with employment status
using the above proportions we have to calculate relative proportion and attributable
proportion. Relative proportion compares the proportion of the employed who underwent
HIV testing to the proportion of the unemployed who underwent HIV testing. (Jorn,
Murray& Ander, 2010) It shows how many times the employed underwent HIV testing
compared to the unemployed
Relative proportion = proportion of the employed who underwe n t HIV testing
proportion of theunemployed who underwent HIV testing

BIOSTATISTICS 7
= 0.5254
0.3396
= 1.5471
From the calculation above the employed are 1.5471 times likely to attend HIV testing compared
to the unemployed.
Attributable proportion is the measure of the health impact of a causative factor (Dicker,
Coronado & Koo, 2006). Attributable proportion shows what percentage of the HIV testing
attendance is associated with employment status.
Attributable proportion =
proportion of employed tested− proportion of unemployed tested
proportionof employed t ested
= 0.5254−0.3394
0.5254
= 0.3540
= 0.3540 x100
= 35.40%
From the above calculation, only 35.40% of the HIV testing attendance is attributed to
employment status. The remaining 64.60% is attributed to other factors. Therefore, undergoing
HIV testing is not associated employment status.
V. A hypothesis is a statement about a characteristic of a population. It concerns itself with
parameters of the population about which the hypothesis statement is made (Rosner,
2010). Hypothesis testing helps the researcher to reach a conclusion about the population

BIOSTATISTICS 8
by examining a sample from the population. (Rosner, 2010). A null hypothesis is a
statement made so as to be put to test. An alternative hypothesis is a statement believed to
be true if the testing done led to the rejection of the null hypothesis.
Null hypothesis: Undergoing HIV testing is not associated with employment status
H0: p1 = p2
H1: p1≠p2
P = ( 59
59+53 x 31
59 ¿+( 53
59+53 x 18
53 )
= 0.2768 + 0.1607
= 0.4375
q = 0.5625
Z= 0.1858
0.09387
= 1. 979

BIOSTATISTICS 9
From the z tables, P-value corresponding to Z = 1.979 is 0. 0478. This value is less than 0.05 and
therefore we reject the null hypothesis. Therefore, there is an association between undergoing
HIV testing and employment status.
Confidence Interval is a pair of numerical values that define an interval that include a certain
parameter to a specific degree of confidence.
C.I
= 0. 1858 ± 1.96 √0.004226+004231
= 0.1858 ± 0.01657
= 0.1692, 0.2024
Therefore, we are 95% confident that the true population difference between the proportion of
employed men undergoing HIV testing and the unemployed men undergoing HIV testing lies
between 0.1692 and 0.2024.
Question 2b.
The odds ratio for the association between HIV testing and being employed is 2.15. This
implies that there is a 2.15 time more likely for an employed person to undergo HIV testing than
an unemployed person.
Question 2c.

BIOSTATISTICS 10
The researcher needs to increase the sample size. This will authenticate the association
between undergoing HIV testing and employment status. A larger sample can be used to
generalize the conclusion to the entire target population. A small sample size may lead to bias or
a false association between the variables. The researcher should also do more measures of
association to ascertain the relationship between undergoing HIV testing and employment status.
The P value obtained from the hypothesis testing was 0.0478. This denotes a weak association
which may have come about by chance.
Question 3: Significance testing
a) Methods that can be used to carry out significance test on the PASI score include
unpaired t-test and analysis of variance, ANOVA. This is because the data provided
by PASI score is numerical as opposed to categorical (Parikh & Hazra, 2010). The
data provided by PASI score is also not paired. This is because it was taken at the end
of the six weeks. If the data was paired, paired t-test and repeated measured ANOVA
could have been used (Wang, Clayton & Bakhai, 2006). From the data given, we
cannot determine a correlation association between the data hence Pearson’s
coefficient and Spearman’s coefficient cannot be used (Petrie& Sabin, 2005).
b) Methods that can be used to carry out significance test on the self-assessment are chi-
square test. This is because the data provided by the self-assessment is categorical as
opposed to numerical (Barun & Hazra, 2011). The data provided is not paired hence
McNemar’s test cannot be used (Wang, Clayton & Bakhai, 2006). If an association
between the parameters are established then odd ratio/risk ratio might be used (Petrie
& Sabin 2005)

BIOSTATISTICS 11
Conclusion
Measures of associations quantify the relationship between two or more variables. They
show whether the association between two or more variables exists and if so to what strength.
Chi-square does not show the strength of the association between the variables. Proportion is a
ratio in which the numerator is a subset of the denominator. The two methods by which
conclusion can be made about a population from a sample is by finding the confidence interval
and hypothesis testing. Deciding what method of significance testing to use involves severally
steps. The steps include deciding whether the data given is numeral or categorical, paired or non-
paired and whether or not there is an association between the variables.
References
Bernard Rosner (2010). Fundamental of Biostatistics. Boston: Brooks/ Cole.
Cohen, J., & Nee, J. C. (2010). Estimators for two measures of association for set
correlation. Educational and Psychological Measurement, 44(4), 907-917.
Dicker, R., Coronado, F., & Koo, D. (2006). Principles of Epidemiology in Public Health
Practice: An introduction to applied epidemiology and biostatistics. Waldorf: PHF.

BIOSTATISTICS 12
Olsen, J., Christensen, K., Murray, J., & Ekbom, A. (2010). An Introduction to Epidemiology for
Health Professionals. New York: Springer
Parikh, M., N., Hazra, A., Mukherjee, J., Gogtay, N. (2010). Research methodology simplified:
Hypothesis testing and choice of statistical test. New Delhi: Jaypee brothers
Petrie, A., Sabin, C. (2005). Medical statistics at a glance. The theory of linear regression and
performing a linear regression analysis. London: Blackwell Publishers.
Wang, D., Clayton, T., & Bakhai, A. (2006). A practical guide to design, analysis, and
reporting. London: Remedica.
Wayne, W., D. (2009). Biostatistics: A foundation for analysis in health sciences. Danvers:
Wiley