Biostatistics Assignment: University of Melbourne POPH90013 Analysis
VerifiedAdded on 2023/01/11
|12
|1355
|94
Homework Assignment
AI Summary
This biostatistics assignment, addressing the "HealthIron" cohort study, presents a detailed analysis of iron-deficiency anemia (IDA) among pre- and post-menopausal women. The solution calculates risk differences, risk ratios, and odds ratios, along with their corresponding confidence intervals, to assess the association between IDA and menopausal status. Furthermore, the assignment extends to analyze the association between living alone and mortality, providing both unadjusted and Mantel-Haenszel adjusted odds ratios, addressing the impact of age at attendance. Additional questions explore the probability of failure in randomized controlled trials and the interpretation of statistical significance in nicotine gum trials, along with an ANOVA analysis. The assignment also delves into the relationship between various factors and cancer diagnosis, including the number of sexual partners, smoking habits, and contraceptive usage, providing a comprehensive statistical overview.

Biostatistics
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Table of Contents
Question 1:.......................................................................................................................................1
Question 3:.......................................................................................................................................2
Question 4:.......................................................................................................................................4
Question 5:.......................................................................................................................................5
Question 1:.......................................................................................................................................1
Question 3:.......................................................................................................................................2
Question 4:.......................................................................................................................................4
Question 5:.......................................................................................................................................5

Question 1:
Participants Iron deficiency anaemia Total
Yes No
Pre-menopausal 213 513 726
Post-menopausal 199 1158 1357
Total 412 1671 2083
(a) Risk difference = a – c
a+b c+d
= 213 – 513
412 1671
= 0.52 – 0.31 = 0.21
(ii) Risk ratio can be calculated by –
a (c+d)/n
c (a+b)/n
= 213 x 1357
199 x 726
= 289041 = 3.34
86394
(iii) Odd ratio can be calculated by –
= ad
bc
= 213 x 1158
199 x 513
= 246654 = 2.41
102087
1
Participants Iron deficiency anaemia Total
Yes No
Pre-menopausal 213 513 726
Post-menopausal 199 1158 1357
Total 412 1671 2083
(a) Risk difference = a – c
a+b c+d
= 213 – 513
412 1671
= 0.52 – 0.31 = 0.21
(ii) Risk ratio can be calculated by –
a (c+d)/n
c (a+b)/n
= 213 x 1357
199 x 726
= 289041 = 3.34
86394
(iii) Odd ratio can be calculated by –
= ad
bc
= 213 x 1158
199 x 513
= 246654 = 2.41
102087
1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

(b)
(i)
SE {RD} = √a x b + c x d
(a + b)3 (c + d)3
= √213 x 199 + 513 x 1158
(412)3 (1671)3
= √0.0005 + 0.0001 = 0.02
95% CI = RD ± 1.96 x SE {RD}
= 0.21 ± 1.96 x 0.02 = 0.17 to 0.25
(ii) SE {In (RR)} = √1 + 1 – 1 – 1
a c a+b c+d
= √1 + 1 – 1 – 1
213 513 412 1671
= √0.005 + 0.002 – 0.002 – 0.001
= 0.06
95% CI = exp (In(RR) ± 1.96 x SE{In(RR)})
= exp (In(3.34) ± 1.96 x 0.06 In(3.34))
= exp (1.21 ± 1.96 x 0.06 x 0.52)
= exp (1.21 ± 0.06)
= 3.15 to 3.56
(iii) SE {In (OR)} = √1 + 1 + 1 + 1
a b c d
= √1 + 1 + 1 + 1
213 199 513 1158
= √0.005 + 0.006 + 0.002 + 0.009 = √0.022 = 0.15
95% CI = exp (In(OR) ± 1.96 x SE{In(OR)})
= exp (In(2.41 ± 1.96 x 0.15 x In(2.41))
= exp (0.88 ± 1.96 x 0.15 x 0.88)
= 0.53 to 3.12
2
(i)
SE {RD} = √a x b + c x d
(a + b)3 (c + d)3
= √213 x 199 + 513 x 1158
(412)3 (1671)3
= √0.0005 + 0.0001 = 0.02
95% CI = RD ± 1.96 x SE {RD}
= 0.21 ± 1.96 x 0.02 = 0.17 to 0.25
(ii) SE {In (RR)} = √1 + 1 – 1 – 1
a c a+b c+d
= √1 + 1 – 1 – 1
213 513 412 1671
= √0.005 + 0.002 – 0.002 – 0.001
= 0.06
95% CI = exp (In(RR) ± 1.96 x SE{In(RR)})
= exp (In(3.34) ± 1.96 x 0.06 In(3.34))
= exp (1.21 ± 1.96 x 0.06 x 0.52)
= exp (1.21 ± 0.06)
= 3.15 to 3.56
(iii) SE {In (OR)} = √1 + 1 + 1 + 1
a b c d
= √1 + 1 + 1 + 1
213 199 513 1158
= √0.005 + 0.006 + 0.002 + 0.009 = √0.022 = 0.15
95% CI = exp (In(OR) ± 1.96 x SE{In(OR)})
= exp (In(2.41 ± 1.96 x 0.15 x In(2.41))
= exp (0.88 ± 1.96 x 0.15 x 0.88)
= 0.53 to 3.12
2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Question 3:
(a) Unadjusted odd ratios for association between living alone and mortality can be calculated by
-
Living alone Died during follow-up Total
Yes No
Yes 852 513 1365
No 655 509 1164
Total 1507 1022 2529
a) Unadjusted or Crude odd ratio can be calculated by –
852 x 509
655 x 513
= 433,668 = 1.29
336015
b) Since present case is based on real life experiment, therefore, it is difficult for analysing the
relationship between variables and the outcome by using adjusted or crude odd ratio. So, it is
better to prefer risk ration as a measure of association between living alone and risk of mortality
under present case. This would provide relatively effective evidence for underpinning the
outcomes.
Living
alone
Age at attendance
>55
Total
Age at attendance
55 years or younger
TotalDied
Yes
Died
No
Died
Yes
Died
No
Yes 540 396 936 312 117 429
No 103 161 264 552 348 900
Total 643 557 1200 864 465 1329
3
(a) Unadjusted odd ratios for association between living alone and mortality can be calculated by
-
Living alone Died during follow-up Total
Yes No
Yes 852 513 1365
No 655 509 1164
Total 1507 1022 2529
a) Unadjusted or Crude odd ratio can be calculated by –
852 x 509
655 x 513
= 433,668 = 1.29
336015
b) Since present case is based on real life experiment, therefore, it is difficult for analysing the
relationship between variables and the outcome by using adjusted or crude odd ratio. So, it is
better to prefer risk ration as a measure of association between living alone and risk of mortality
under present case. This would provide relatively effective evidence for underpinning the
outcomes.
Living
alone
Age at attendance
>55
Total
Age at attendance
55 years or younger
TotalDied
Yes
Died
No
Died
Yes
Died
No
Yes 540 396 936 312 117 429
No 103 161 264 552 348 900
Total 643 557 1200 864 465 1329
3

(c) Unadjusted or Crude odd ratio for age at attendance >55 can be calculated by –
540 x 161
103 x 396
= 86940 = 2.13
40788
Unadjusted or Crude odd ratio for age at attendance 55 or younger can be calculated by –
312 x 348
552 x 117
= 108576 = 1.68
64584
(d) Mantel-Haenszel estimate of pooled odds ratio can be calculated by –
RRcmh = Σ a d/n
Σ b c /n
= 540 x 161 + 312 x 348
1200 1329
103 x 396 + 552 x 117
1200 1329
= 72.45 + 81.69 = 154.14
33.99 + 48.71 82.7
= 1.86
4
540 x 161
103 x 396
= 86940 = 2.13
40788
Unadjusted or Crude odd ratio for age at attendance 55 or younger can be calculated by –
312 x 348
552 x 117
= 108576 = 1.68
64584
(d) Mantel-Haenszel estimate of pooled odds ratio can be calculated by –
RRcmh = Σ a d/n
Σ b c /n
= 540 x 161 + 312 x 348
1200 1329
103 x 396 + 552 x 117
1200 1329
= 72.45 + 81.69 = 154.14
33.99 + 48.71 82.7
= 1.86
4
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Question 4:
(a) The probability of failure of the randomised controlled trial for detecting a true risk
difference of 10% is high, because the modest reduction in risk of the unfavourable outcomes,
may cause major public health significance.
(b) In order to reduce the probability of failing to detect a true of risk difference of 10% units,
quality of evidence need to be improved. For this purpose, a 50% control event, with 95% power
at a 0.05 level of significance needs to be set. Along with this, optimal information size is also
needed for reliably detecting the same.
5
(a) The probability of failure of the randomised controlled trial for detecting a true risk
difference of 10% is high, because the modest reduction in risk of the unfavourable outcomes,
may cause major public health significance.
(b) In order to reduce the probability of failing to detect a true of risk difference of 10% units,
quality of evidence need to be improved. For this purpose, a 50% control event, with 95% power
at a 0.05 level of significance needs to be set. Along with this, optimal information size is also
needed for reliably detecting the same.
5
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Question 5:
(a) Age group of smokers is missing from the report, which is essential to clinically obtain the
efficiency of result.
(b) As only providing the statistical significance result is not enough to translate the clinical
importance therefore, in given case of nicotine gum, stating p<0.05, is not sufficient, to interpret
the outcomes.
Question 6
a) 2.10%
b) Who have 2 numbers of pregnancies
c) 11.47%
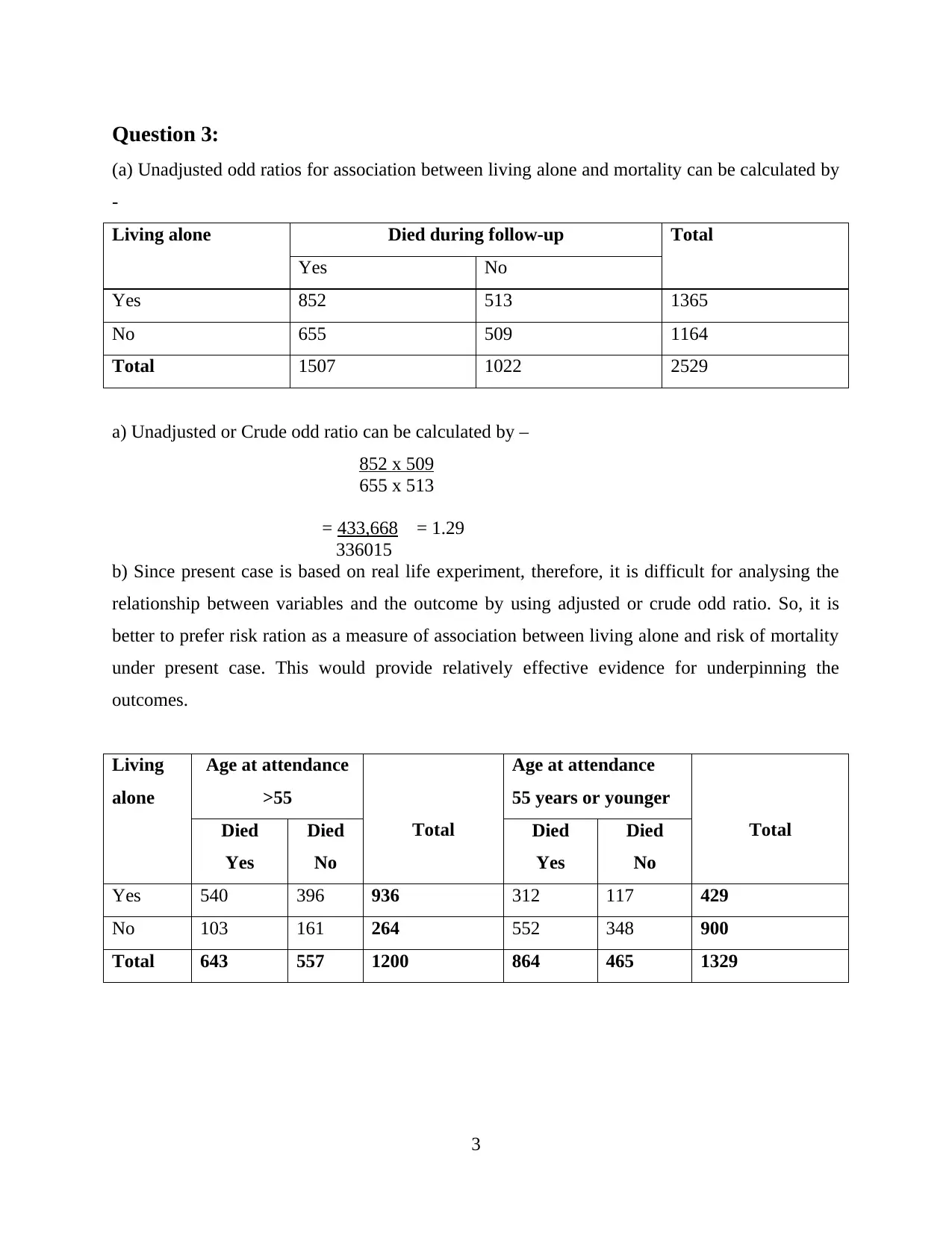
d)
There is no asssociation between two, but this disease is common among the girls age between
18 to 19, during having first sex.
e)
6
(a) Age group of smokers is missing from the report, which is essential to clinically obtain the
efficiency of result.
(b) As only providing the statistical significance result is not enough to translate the clinical
importance therefore, in given case of nicotine gum, stating p<0.05, is not sufficient, to interpret
the outcomes.
Question 6
a) 2.10%
b) Who have 2 numbers of pregnancies
c) 11.47%
d)
There is no asssociation between two, but this disease is common among the girls age between
18 to 19, during having first sex.
e)
6
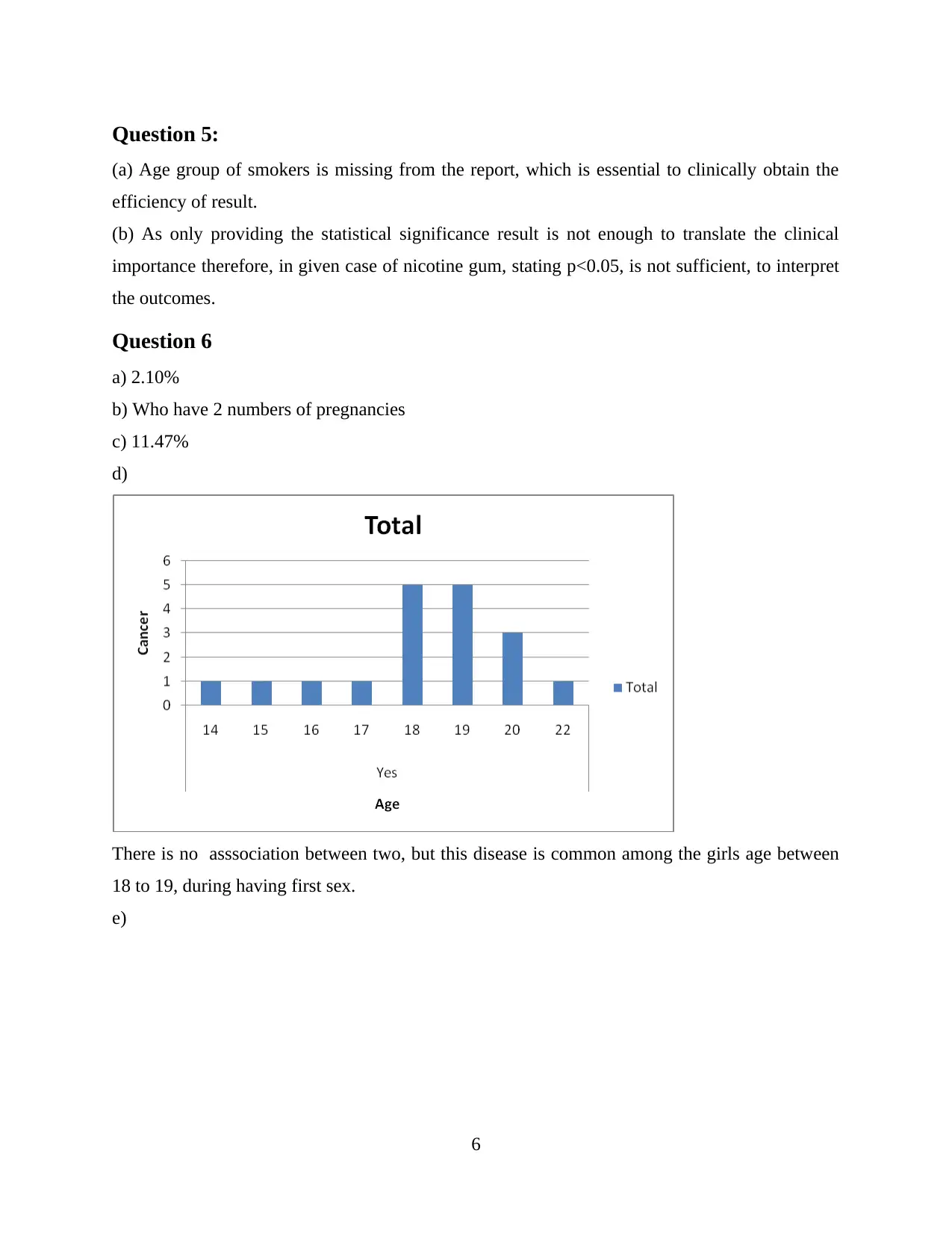
There’s no association between two variables; very few females uses contraceptives to diagnosed
cancer.
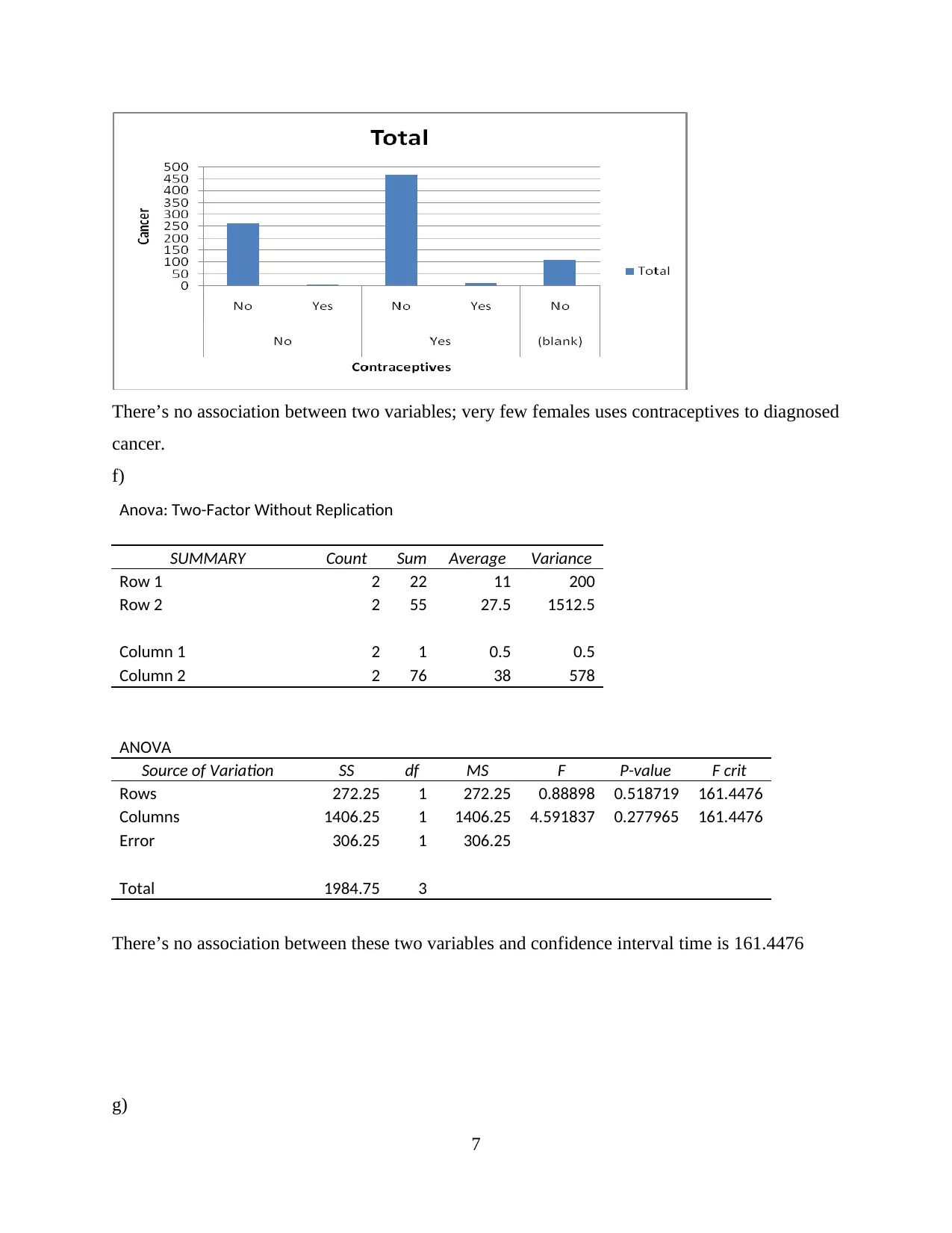
f)
Anova: Two-Factor Without Replication
SUMMARY Count Sum Average Variance
Row 1 2 22 11 200
Row 2 2 55 27.5 1512.5
Column 1 2 1 0.5 0.5
Column 2 2 76 38 578
ANOVA
Source of Variation SS df MS F P-value F crit
Rows 272.25 1 272.25 0.88898 0.518719 161.4476
Columns 1406.25 1 1406.25 4.591837 0.277965 161.4476
Error 306.25 1 306.25
Total 1984.75 3
There’s no association between these two variables and confidence interval time is 161.4476
g)
7
cancer.
f)
Anova: Two-Factor Without Replication
SUMMARY Count Sum Average Variance
Row 1 2 22 11 200
Row 2 2 55 27.5 1512.5
Column 1 2 1 0.5 0.5
Column 2 2 76 38 578
ANOVA
Source of Variation SS df MS F P-value F crit
Rows 272.25 1 272.25 0.88898 0.518719 161.4476
Columns 1406.25 1 1406.25 4.591837 0.277965 161.4476
Error 306.25 1 306.25
Total 1984.75 3
There’s no association between these two variables and confidence interval time is 161.4476
g)
7
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
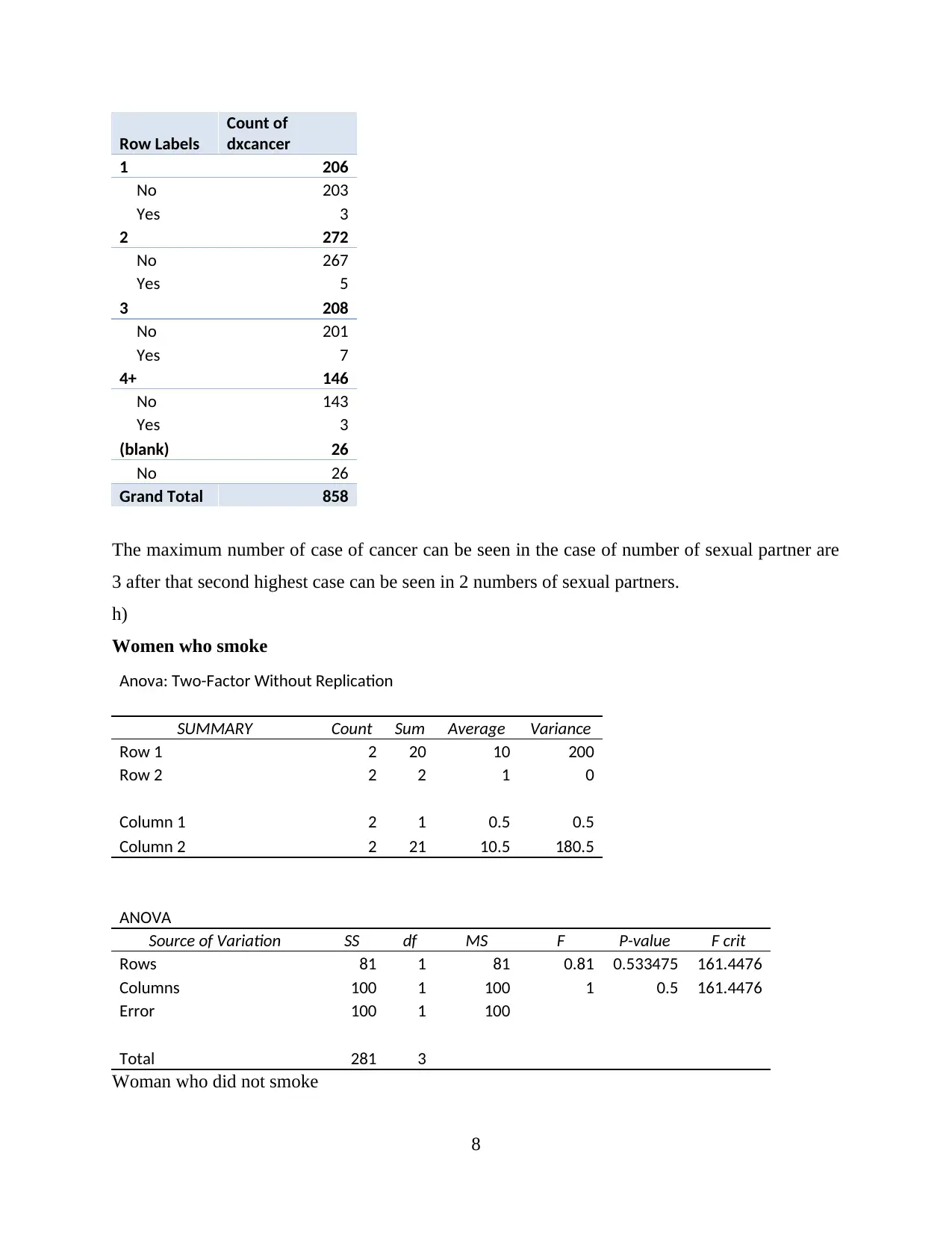
Row Labels
Count of
dxcancer
1 206
No 203
Yes 3
2 272
No 267
Yes 5
3 208
No 201
Yes 7
4+ 146
No 143
Yes 3
(blank) 26
No 26
Grand Total 858
The maximum number of case of cancer can be seen in the case of number of sexual partner are
3 after that second highest case can be seen in 2 numbers of sexual partners.
h)
Women who smoke
Anova: Two-Factor Without Replication
SUMMARY Count Sum Average Variance
Row 1 2 20 10 200
Row 2 2 2 1 0
Column 1 2 1 0.5 0.5
Column 2 2 21 10.5 180.5
ANOVA
Source of Variation SS df MS F P-value F crit
Rows 81 1 81 0.81 0.533475 161.4476
Columns 100 1 100 1 0.5 161.4476
Error 100 1 100
Total 281 3
Woman who did not smoke
8
Count of
dxcancer
1 206
No 203
Yes 3
2 272
No 267
Yes 5
3 208
No 201
Yes 7
4+ 146
No 143
Yes 3
(blank) 26
No 26
Grand Total 858
The maximum number of case of cancer can be seen in the case of number of sexual partner are
3 after that second highest case can be seen in 2 numbers of sexual partners.
h)
Women who smoke
Anova: Two-Factor Without Replication
SUMMARY Count Sum Average Variance
Row 1 2 20 10 200
Row 2 2 2 1 0
Column 1 2 1 0.5 0.5
Column 2 2 21 10.5 180.5
ANOVA
Source of Variation SS df MS F P-value F crit
Rows 81 1 81 0.81 0.533475 161.4476
Columns 100 1 100 1 0.5 161.4476
Error 100 1 100
Total 281 3
Woman who did not smoke
8
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Anova: Two-Factor Without Replication
9
9

SUMMARY Count Sum Average Variance
Row 1 2 54 27 1458
Row 2 2 2 1 0
Column 1 2 1 0.5 0.5
Column 2 2 55 27.5 1404.5
ANOVA
Source of Variation SS df MS F P-value F crit
Rows 676 1 676 0.927298 0.51201 161.4476
Columns 729 1 729 1 0.5 161.4476
Error 729 1 729
Total 2134 3
i)
Row Labels
Count of
dxcancer
Ever 123
No 86
No 85
Yes 1
Yes 21
No 20
Yes 1
(blank) 16
No 16
Never 722
No 581
No 567
Yes 14
Yes 55
No 54
Yes 1
(blank) 86
No 86
(blank) 13
No 7
No 6
Yes 1
10
Row 1 2 54 27 1458
Row 2 2 2 1 0
Column 1 2 1 0.5 0.5
Column 2 2 55 27.5 1404.5
ANOVA
Source of Variation SS df MS F P-value F crit
Rows 676 1 676 0.927298 0.51201 161.4476
Columns 729 1 729 1 0.5 161.4476
Error 729 1 729
Total 2134 3
i)
Row Labels
Count of
dxcancer
Ever 123
No 86
No 85
Yes 1
Yes 21
No 20
Yes 1
(blank) 16
No 16
Never 722
No 581
No 567
Yes 14
Yes 55
No 54
Yes 1
(blank) 86
No 86
(blank) 13
No 7
No 6
Yes 1
10
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.