Problemsolving and modelling task Bivariate Data
VerifiedAdded on 2023/06/18
|11
|1847
|343
AI Summary
This report analyses the height of offspring dependent upon the height of their parents using regression analysis and correlation coefficient. The report verifies the findings of Sally's research and discusses the limitations of the method used. The sample size, raw data, and formulae used are also provided.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Problemsolving and modelling task
Bivariate Data
Bivariate Data
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

TABLE OF CONTENTS
INTRODUCTION......................................................................................................................3
FORMULATE...........................................................................................................................3
Observation............................................................................................................................3
Assumptions...........................................................................................................................3
The plan..................................................................................................................................3
Sample Formula’s..................................................................................................................3
Sample Size............................................................................................................................4
SOLVE.......................................................................................................................................4
Raw data.................................................................................................................................4
Calculating equation of line...................................................................................................4
Discussing Sally’s model.......................................................................................................5
Understanding and plotting on the new data..........................................................................5
Justification of decision using mathematical reasoning.........................................................7
Evaluate and verify................................................................................................................7
CONCLUSION..........................................................................................................................8
REFERENCES...........................................................................................................................9
APPENDIX..............................................................................................................................10
INTRODUCTION......................................................................................................................3
FORMULATE...........................................................................................................................3
Observation............................................................................................................................3
Assumptions...........................................................................................................................3
The plan..................................................................................................................................3
Sample Formula’s..................................................................................................................3
Sample Size............................................................................................................................4
SOLVE.......................................................................................................................................4
Raw data.................................................................................................................................4
Calculating equation of line...................................................................................................4
Discussing Sally’s model.......................................................................................................5
Understanding and plotting on the new data..........................................................................5
Justification of decision using mathematical reasoning.........................................................7
Evaluate and verify................................................................................................................7
CONCLUSION..........................................................................................................................8
REFERENCES...........................................................................................................................9
APPENDIX..............................................................................................................................10

INTRODUCTION
The problem solving refers to the skills which is being used for the purpose of
effectively analysing the data available. In this report, an investigation is being carried out
pertaining to analysing the height of offspring is dependent upon the height of their parents.
Sally has conducted this research and this report will throw light on determining whether the
findings of Sally is right or not. In order to complete this task effectively certain steps and
structure will be followed which will involve observation and assumptions.
FORMULATE
Observation
There are certain observations which are being made towards the task which are
given below:
Children mostly resembles their parents.
Most of the children have mainly resembling to their mother in comparison to their
father.
There is minor difference in the height of the daughter and mother but in most case
there is vast difference in height between daughter and father.
Assumptions
There are certain parameters which are required to be assumed in order to conduct
this research effectively.
The students have attained the maximum height.
There is no further scope of increase in height.
Both father and the mother are equally exposed to environmental factors.
The data provided is conclusive in nature.
The plan
Firstly, the data will be organized in a well-structured format which will help in
getting better insight in the data.
The data analytical tools which will be utilized for attaining the desired outcomes will
be selected. This is important as it will help in determining the outcomes associated
with each of the method. So that the right approach can be selected.
The key variables that will be used is the number of students, height of the daughter
and the height of the mother. The formula for equation line will be used y=mx+c.
Sample Formula’s
Equation of the line y = mx + c
The problem solving refers to the skills which is being used for the purpose of
effectively analysing the data available. In this report, an investigation is being carried out
pertaining to analysing the height of offspring is dependent upon the height of their parents.
Sally has conducted this research and this report will throw light on determining whether the
findings of Sally is right or not. In order to complete this task effectively certain steps and
structure will be followed which will involve observation and assumptions.
FORMULATE
Observation
There are certain observations which are being made towards the task which are
given below:
Children mostly resembles their parents.
Most of the children have mainly resembling to their mother in comparison to their
father.
There is minor difference in the height of the daughter and mother but in most case
there is vast difference in height between daughter and father.
Assumptions
There are certain parameters which are required to be assumed in order to conduct
this research effectively.
The students have attained the maximum height.
There is no further scope of increase in height.
Both father and the mother are equally exposed to environmental factors.
The data provided is conclusive in nature.
The plan
Firstly, the data will be organized in a well-structured format which will help in
getting better insight in the data.
The data analytical tools which will be utilized for attaining the desired outcomes will
be selected. This is important as it will help in determining the outcomes associated
with each of the method. So that the right approach can be selected.
The key variables that will be used is the number of students, height of the daughter
and the height of the mother. The formula for equation line will be used y=mx+c.
Sample Formula’s
Equation of the line y = mx + c
Correlation coefficient r = n(Σxy) – (Σx)( Σy)
Sqrt [n Σx^2 – (Σx)^2] [n Σy^2 – (Σy)^2]
Sample Size
The selected sample size is 20 students which will be representing the entire
population. As this will help in better analysis of the sample data. In the creation of this
random data set, randbetween formula is being used for selecting the sample of 25 students
which were later trim down to 20 students.
SOLVE
Raw data
Attached in appendix.
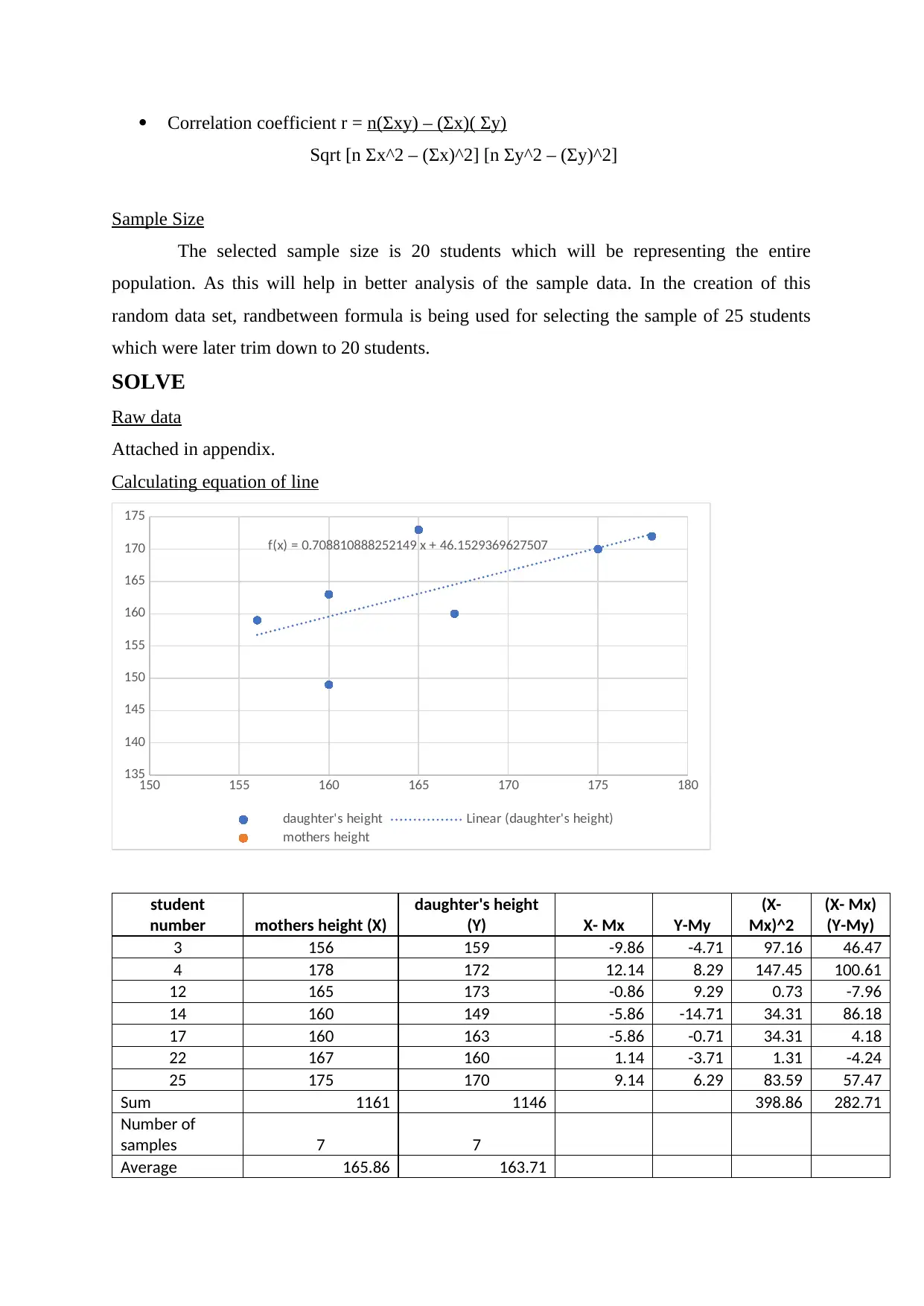
Calculating equation of line
150 155 160 165 170 175 180
135
140
145
150
155
160
165
170
175
f(x) = 0.708810888252149 x + 46.1529369627507
daughter's height Linear (daughter's height)
mothers height
student
number mothers height (X)
daughter's height
(Y) X- Mx Y-My
(X-
Mx)^2
(X- Mx)
(Y-My)
3 156 159 -9.86 -4.71 97.16 46.47
4 178 172 12.14 8.29 147.45 100.61
12 165 173 -0.86 9.29 0.73 -7.96
14 160 149 -5.86 -14.71 34.31 86.18
17 160 163 -5.86 -0.71 34.31 4.18
22 167 160 1.14 -3.71 1.31 -4.24
25 175 170 9.14 6.29 83.59 57.47
Sum 1161 1146 398.86 282.71
Number of
samples 7 7
Average 165.86 163.71
Sqrt [n Σx^2 – (Σx)^2] [n Σy^2 – (Σy)^2]
Sample Size
The selected sample size is 20 students which will be representing the entire
population. As this will help in better analysis of the sample data. In the creation of this
random data set, randbetween formula is being used for selecting the sample of 25 students
which were later trim down to 20 students.
SOLVE
Raw data
Attached in appendix.
Calculating equation of line
150 155 160 165 170 175 180
135
140
145
150
155
160
165
170
175
f(x) = 0.708810888252149 x + 46.1529369627507
daughter's height Linear (daughter's height)
mothers height
student
number mothers height (X)
daughter's height
(Y) X- Mx Y-My
(X-
Mx)^2
(X- Mx)
(Y-My)
3 156 159 -9.86 -4.71 97.16 46.47
4 178 172 12.14 8.29 147.45 100.61
12 165 173 -0.86 9.29 0.73 -7.96
14 160 149 -5.86 -14.71 34.31 86.18
17 160 163 -5.86 -0.71 34.31 4.18
22 167 160 1.14 -3.71 1.31 -4.24
25 175 170 9.14 6.29 83.59 57.47
Sum 1161 1146 398.86 282.71
Number of
samples 7 7
Average 165.86 163.71
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Regression Equation = ŷ = mX + c
m = SP/SSx = 282.71/398.86 = 0.70881
c = My - bMx = 163.71 - (0.71*165.86) = 46.15294
ŷ = 0.70881X + 46.15294
Correlation coefficient (using excel)
mothers
height (X)
daughter'
s height
(Y)
Mother’s height (X) 1
Daughter's height
(Y) 0.66923279 1
Discussing Sally’s model
This is a moderate positive correlation, which means there is a tendency for high X variable
scores go with high Y variable scores (and vice versa). The limitation of this method is that it
does not look at the effects of the other variables outside of these two (Gogtay and Thatte,
2017). It cannot describe the curvilinear relationships.
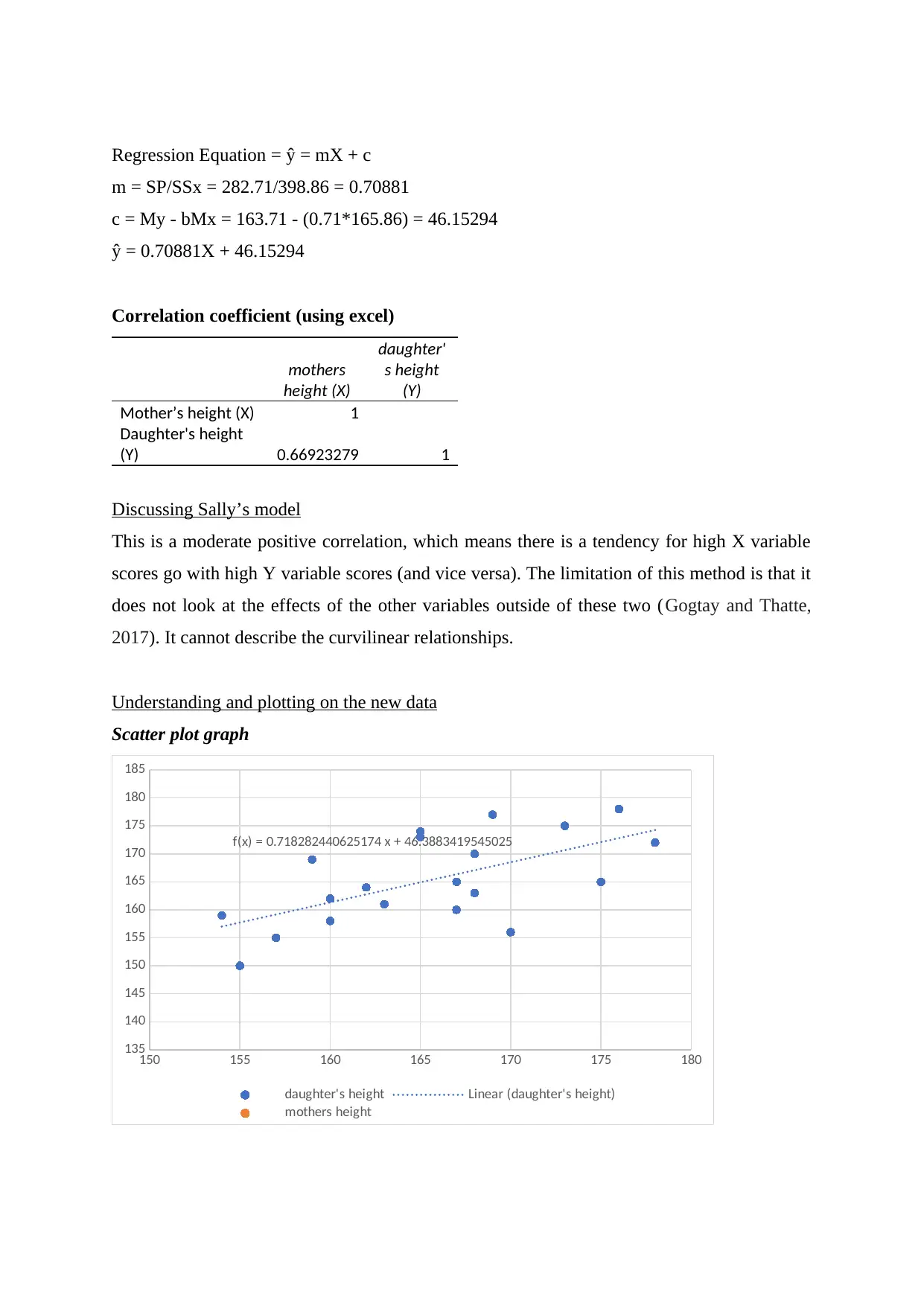
Understanding and plotting on the new data
Scatter plot graph
150 155 160 165 170 175 180
135
140
145
150
155
160
165
170
175
180
185
f(x) = 0.718282440625174 x + 46.3883419545025
daughter's height Linear (daughter's height)
mothers height
m = SP/SSx = 282.71/398.86 = 0.70881
c = My - bMx = 163.71 - (0.71*165.86) = 46.15294
ŷ = 0.70881X + 46.15294
Correlation coefficient (using excel)
mothers
height (X)
daughter'
s height
(Y)
Mother’s height (X) 1
Daughter's height
(Y) 0.66923279 1
Discussing Sally’s model
This is a moderate positive correlation, which means there is a tendency for high X variable
scores go with high Y variable scores (and vice versa). The limitation of this method is that it
does not look at the effects of the other variables outside of these two (Gogtay and Thatte,
2017). It cannot describe the curvilinear relationships.
Understanding and plotting on the new data
Scatter plot graph
150 155 160 165 170 175 180
135
140
145
150
155
160
165
170
175
180
185
f(x) = 0.718282440625174 x + 46.3883419545025
daughter's height Linear (daughter's height)
mothers height
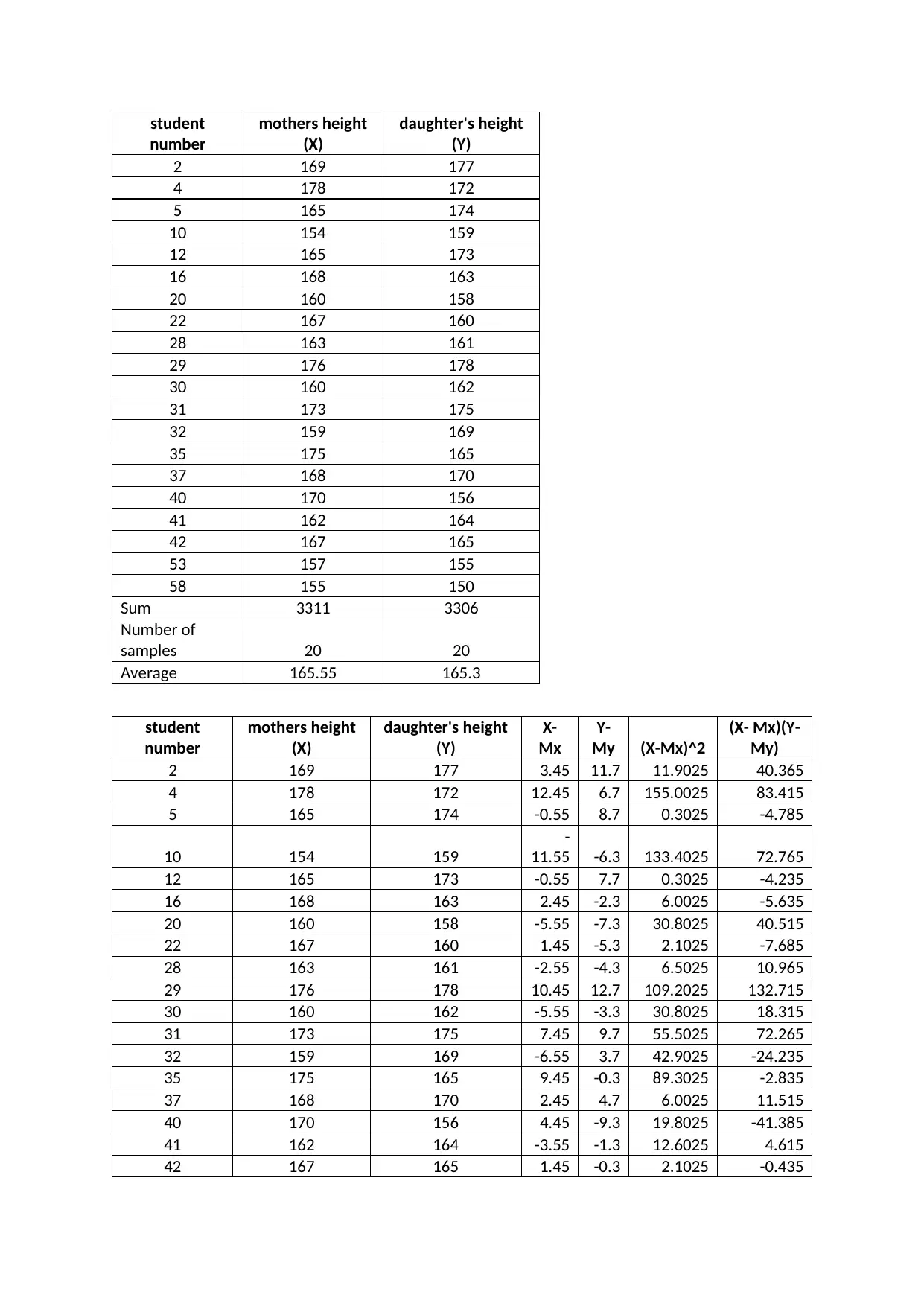
student
number
mothers height
(X)
daughter's height
(Y)
2 169 177
4 178 172
5 165 174
10 154 159
12 165 173
16 168 163
20 160 158
22 167 160
28 163 161
29 176 178
30 160 162
31 173 175
32 159 169
35 175 165
37 168 170
40 170 156
41 162 164
42 167 165
53 157 155
58 155 150
Sum 3311 3306
Number of
samples 20 20
Average 165.55 165.3
student
number
mothers height
(X)
daughter's height
(Y)
X-
Mx
Y-
My (X-Mx)^2
(X- Mx)(Y-
My)
2 169 177 3.45 11.7 11.9025 40.365
4 178 172 12.45 6.7 155.0025 83.415
5 165 174 -0.55 8.7 0.3025 -4.785
10 154 159
-
11.55 -6.3 133.4025 72.765
12 165 173 -0.55 7.7 0.3025 -4.235
16 168 163 2.45 -2.3 6.0025 -5.635
20 160 158 -5.55 -7.3 30.8025 40.515
22 167 160 1.45 -5.3 2.1025 -7.685
28 163 161 -2.55 -4.3 6.5025 10.965
29 176 178 10.45 12.7 109.2025 132.715
30 160 162 -5.55 -3.3 30.8025 18.315
31 173 175 7.45 9.7 55.5025 72.265
32 159 169 -6.55 3.7 42.9025 -24.235
35 175 165 9.45 -0.3 89.3025 -2.835
37 168 170 2.45 4.7 6.0025 11.515
40 170 156 4.45 -9.3 19.8025 -41.385
41 162 164 -3.55 -1.3 12.6025 4.615
42 167 165 1.45 -0.3 2.1025 -0.435
number
mothers height
(X)
daughter's height
(Y)
2 169 177
4 178 172
5 165 174
10 154 159
12 165 173
16 168 163
20 160 158
22 167 160
28 163 161
29 176 178
30 160 162
31 173 175
32 159 169
35 175 165
37 168 170
40 170 156
41 162 164
42 167 165
53 157 155
58 155 150
Sum 3311 3306
Number of
samples 20 20
Average 165.55 165.3
student
number
mothers height
(X)
daughter's height
(Y)
X-
Mx
Y-
My (X-Mx)^2
(X- Mx)(Y-
My)
2 169 177 3.45 11.7 11.9025 40.365
4 178 172 12.45 6.7 155.0025 83.415
5 165 174 -0.55 8.7 0.3025 -4.785
10 154 159
-
11.55 -6.3 133.4025 72.765
12 165 173 -0.55 7.7 0.3025 -4.235
16 168 163 2.45 -2.3 6.0025 -5.635
20 160 158 -5.55 -7.3 30.8025 40.515
22 167 160 1.45 -5.3 2.1025 -7.685
28 163 161 -2.55 -4.3 6.5025 10.965
29 176 178 10.45 12.7 109.2025 132.715
30 160 162 -5.55 -3.3 30.8025 18.315
31 173 175 7.45 9.7 55.5025 72.265
32 159 169 -6.55 3.7 42.9025 -24.235
35 175 165 9.45 -0.3 89.3025 -2.835
37 168 170 2.45 4.7 6.0025 11.515
40 170 156 4.45 -9.3 19.8025 -41.385
41 162 164 -3.55 -1.3 12.6025 4.615
42 167 165 1.45 -0.3 2.1025 -0.435

53 157 155 -8.55
-
10.3 73.1025 88.065
58 155 150
-
10.55
-
15.3 111.3025 161.415
Sum 3311 3306 898.95 645.7
Regression Equation = ŷ = mX + c
m = SP/SSX = 645.7/898.95 = 0.71828
c = My - bMx = 165.3 - (0.72*165.55) = 46.38834
ŷ = 0.71828X + 46.38834
Correlation coefficient (using excel)
Mother’s height (X) Daughter's height (Y)
Mother’s height (X) 1
Daughter's height
(Y) 0.623718261 1
Both the graphs display the same trend or pattern which indicates that the Sally’s maths is
correct.
Justification of decision using mathematical reasoning
The selected sample size is larger than the one selected by Sally which results into
providing more accurate or deviating outcomes (Montgomery, Peck and Vining, 2021). But
the large sample size which is selected randomly has resulted into providing more accurate
and reliable outcomes.
Evaluate and verify
The solution provided with the new data set helped in making sure that the outcome
derived by Sally is right or not. The solution provided is conclusive in nature which might be
affected if more large data is selected. The strength of regression model is that it helps in
determining the level of dependency one variable is having on the another but on the other
side, it is a complex process pertaining to calculation and analysis (Mu, Liu and Wang,
2018). The sample size could have been further expanded which would have resulted into
getting more accurate outcomes (Kumari and Yadav, 2018). The weakness of Pearson’s
correlation coefficient is that it does not tell about the cause and effect relationship between
the two. It can be very easily misinterpreted as the higher degree of correlation derived from
the large values of the correlation coefficient does not always mean high linear relationship
among the variables. In addition to this, it is a very time consuming process.
-
10.3 73.1025 88.065
58 155 150
-
10.55
-
15.3 111.3025 161.415
Sum 3311 3306 898.95 645.7
Regression Equation = ŷ = mX + c
m = SP/SSX = 645.7/898.95 = 0.71828
c = My - bMx = 165.3 - (0.72*165.55) = 46.38834
ŷ = 0.71828X + 46.38834
Correlation coefficient (using excel)
Mother’s height (X) Daughter's height (Y)
Mother’s height (X) 1
Daughter's height
(Y) 0.623718261 1
Both the graphs display the same trend or pattern which indicates that the Sally’s maths is
correct.
Justification of decision using mathematical reasoning
The selected sample size is larger than the one selected by Sally which results into
providing more accurate or deviating outcomes (Montgomery, Peck and Vining, 2021). But
the large sample size which is selected randomly has resulted into providing more accurate
and reliable outcomes.
Evaluate and verify
The solution provided with the new data set helped in making sure that the outcome
derived by Sally is right or not. The solution provided is conclusive in nature which might be
affected if more large data is selected. The strength of regression model is that it helps in
determining the level of dependency one variable is having on the another but on the other
side, it is a complex process pertaining to calculation and analysis (Mu, Liu and Wang,
2018). The sample size could have been further expanded which would have resulted into
getting more accurate outcomes (Kumari and Yadav, 2018). The weakness of Pearson’s
correlation coefficient is that it does not tell about the cause and effect relationship between
the two. It can be very easily misinterpreted as the higher degree of correlation derived from
the large values of the correlation coefficient does not always mean high linear relationship
among the variables. In addition to this, it is a very time consuming process.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

CONCLUSION
It can be concluded rom the above analysis that the outcome or the math used by
sally is right and the research pertaining to the topic that the height of offspring depend upon
their parents have proved to be right. There are various techniques like regression analysis
which is being used in order to know the line of best fit. In order to verify the reasonableness
of the result model is being refined by undertaking new samples and carrying out the research
on the same.
It can be concluded rom the above analysis that the outcome or the math used by
sally is right and the research pertaining to the topic that the height of offspring depend upon
their parents have proved to be right. There are various techniques like regression analysis
which is being used in order to know the line of best fit. In order to verify the reasonableness
of the result model is being refined by undertaking new samples and carrying out the research
on the same.

REFERENCES
Books and Journals
Gogtay, N. J. and Thatte, U. M., 2017. Principles of correlation analysis. Journal of the
Association of Physicians of India. 65(3). pp.78-81.
Kumari, K. and Yadav, S., 2018. Linear regression analysis study. Journal of the practice of
Cardiovascular Sciences. 4(1). p.33.
Montgomery, D. C., Peck, E. A. and Vining, G. G., 2021. Introduction to linear regression
analysis. John Wiley & Sons.
Mu, Y., Liu, X. and Wang, L., 2018. A Pearson’s correlation coefficient based decision tree
and its parallel implementation. Information Sciences. 435. pp.40-58.
Books and Journals
Gogtay, N. J. and Thatte, U. M., 2017. Principles of correlation analysis. Journal of the
Association of Physicians of India. 65(3). pp.78-81.
Kumari, K. and Yadav, S., 2018. Linear regression analysis study. Journal of the practice of
Cardiovascular Sciences. 4(1). p.33.
Montgomery, D. C., Peck, E. A. and Vining, G. G., 2021. Introduction to linear regression
analysis. John Wiley & Sons.
Mu, Y., Liu, X. and Wang, L., 2018. A Pearson’s correlation coefficient based decision tree
and its parallel implementation. Information Sciences. 435. pp.40-58.
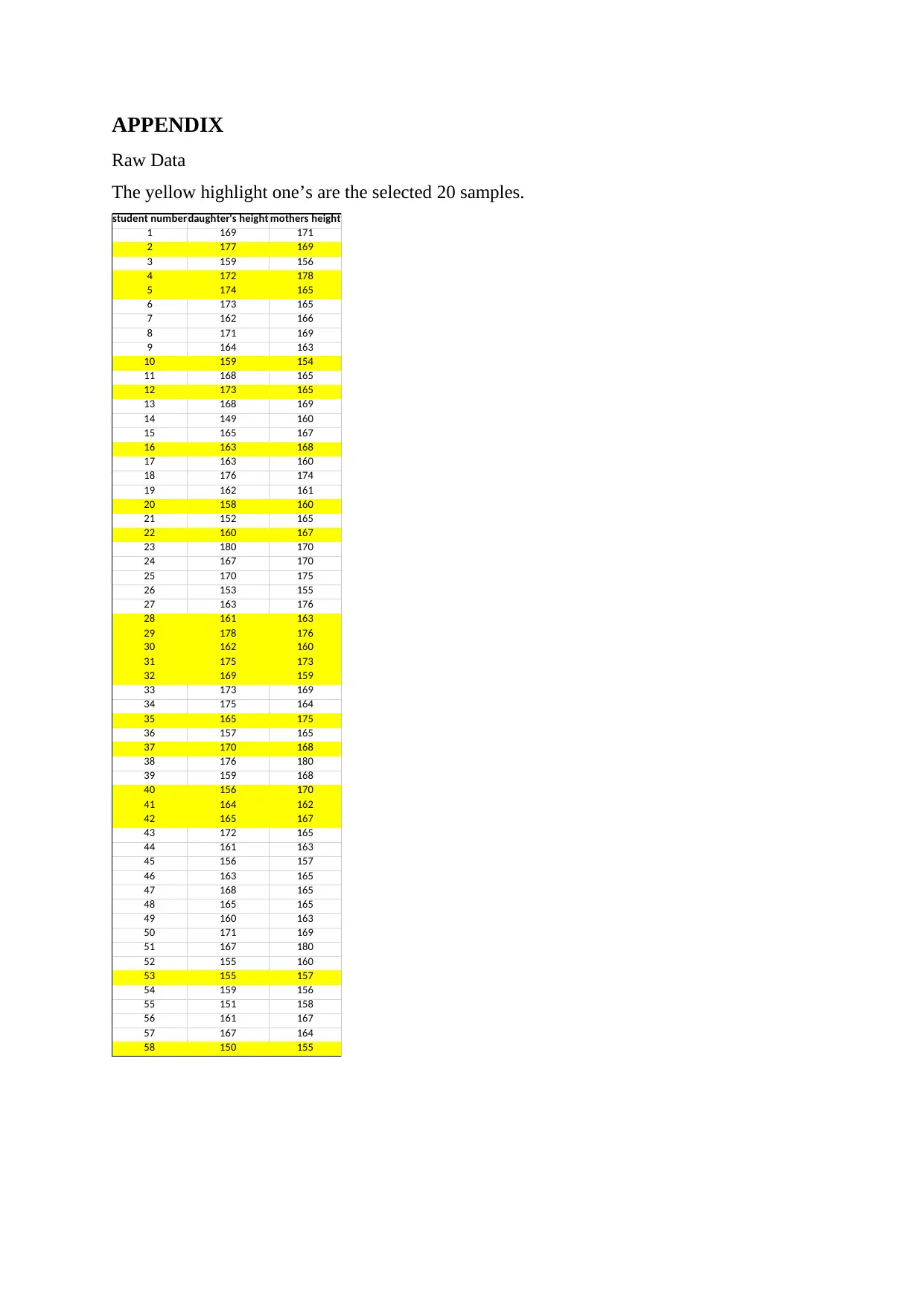
APPENDIX
Raw Data
The yellow highlight one’s are the selected 20 samples.
student numberdaughter's height mothers height
1 169 171
2 177 169
3 159 156
4 172 178
5 174 165
6 173 165
7 162 166
8 171 169
9 164 163
10 159 154
11 168 165
12 173 165
13 168 169
14 149 160
15 165 167
16 163 168
17 163 160
18 176 174
19 162 161
20 158 160
21 152 165
22 160 167
23 180 170
24 167 170
25 170 175
26 153 155
27 163 176
28 161 163
29 178 176
30 162 160
31 175 173
32 169 159
33 173 169
34 175 164
35 165 175
36 157 165
37 170 168
38 176 180
39 159 168
40 156 170
41 164 162
42 165 167
43 172 165
44 161 163
45 156 157
46 163 165
47 168 165
48 165 165
49 160 163
50 171 169
51 167 180
52 155 160
53 155 157
54 159 156
55 151 158
56 161 167
57 167 164
58 150 155
Raw Data
The yellow highlight one’s are the selected 20 samples.
student numberdaughter's height mothers height
1 169 171
2 177 169
3 159 156
4 172 178
5 174 165
6 173 165
7 162 166
8 171 169
9 164 163
10 159 154
11 168 165
12 173 165
13 168 169
14 149 160
15 165 167
16 163 168
17 163 160
18 176 174
19 162 161
20 158 160
21 152 165
22 160 167
23 180 170
24 167 170
25 170 175
26 153 155
27 163 176
28 161 163
29 178 176
30 162 160
31 175 173
32 169 159
33 173 169
34 175 164
35 165 175
36 157 165
37 170 168
38 176 180
39 159 168
40 156 170
41 164 162
42 165 167
43 172 165
44 161 163
45 156 157
46 163 165
47 168 165
48 165 165
49 160 163
50 171 169
51 167 180
52 155 160
53 155 157
54 159 156
55 151 158
56 161 167
57 167 164
58 150 155
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.