Quantum Mechanical Model of Hydrogen Atom
VerifiedAdded on 2023/04/23
|11
|2213
|470
AI Summary
This article discusses the Quantum Mechanical Model of Hydrogen Atom, its introduction, postulates, and limitations. It explains the wave-particle duality of electrons and the Heisenberg uncertainty principle. It explores the Quantum Mechanical Tunnelling Effect and its applications. The article also provides references for further reading.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

1
Q.M. Model of H - Atom
Quantum Mechanical Model of Hydrogen Atom
Q.M. Model of H - Atom
Quantum Mechanical Model of Hydrogen Atom
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

2
Q.M. Model of H - Atom
Introduction
After the failure of the Rutherford model of an atom proposed in 1911
which was not able to explain the stability of the atom; Niels Bohr, a
Danish Physicist, suggested in 1913 that the electrons could only orbit
in discrete orbits or shells with a constant radius around the nucleus. The
electron could not exist in between these shells and occupy only those
shells whose radius is given by Bohr’s Formula. According to Friedrich
(2006), though the model successfully explained the Hydrogen Spectra
precisely, it was not able to explain Zeeman Effect, Heisenberg
Uncertainty Principle and atomic spectra of heavy atoms. Further, the
model was modified by the Introduction of new field of Physics namely
Quantum Mechanics.
Quantum Mechanical Model of Atom
1. Classical and Quantum Mechanical Models: According to Verma
(1993) , the Classical Model for an atom suggests that the electron
revolving around the nucleus is a particle and the force governing its
motion is Electrostatic force of attraction. On the other hand, the
quantum model for electron defines electron as a wave with wavefunction
ψ ( x , t ) square of which gives us the probability of locating the electron at
the position (x) as given in Gasiorowicz (2007). Before the evolution of
quantum mechanics, Neils Bohr gave 3 postulates regarding motion of
electron in an atom. As stated in Saraswati (2017), these were-
a. An electron can revolve around the nucleus in certain fixed orbits of
definite energy without emission of any radiant energy. Such orbits are
called stationary orbits.
Q.M. Model of H - Atom
Introduction
After the failure of the Rutherford model of an atom proposed in 1911
which was not able to explain the stability of the atom; Niels Bohr, a
Danish Physicist, suggested in 1913 that the electrons could only orbit
in discrete orbits or shells with a constant radius around the nucleus. The
electron could not exist in between these shells and occupy only those
shells whose radius is given by Bohr’s Formula. According to Friedrich
(2006), though the model successfully explained the Hydrogen Spectra
precisely, it was not able to explain Zeeman Effect, Heisenberg
Uncertainty Principle and atomic spectra of heavy atoms. Further, the
model was modified by the Introduction of new field of Physics namely
Quantum Mechanics.
Quantum Mechanical Model of Atom
1. Classical and Quantum Mechanical Models: According to Verma
(1993) , the Classical Model for an atom suggests that the electron
revolving around the nucleus is a particle and the force governing its
motion is Electrostatic force of attraction. On the other hand, the
quantum model for electron defines electron as a wave with wavefunction
ψ ( x , t ) square of which gives us the probability of locating the electron at
the position (x) as given in Gasiorowicz (2007). Before the evolution of
quantum mechanics, Neils Bohr gave 3 postulates regarding motion of
electron in an atom. As stated in Saraswati (2017), these were-
a. An electron can revolve around the nucleus in certain fixed orbits of
definite energy without emission of any radiant energy. Such orbits are
called stationary orbits.

3
Q.M. Model of H - Atom
b. An electron can make a transition in the atom from a stationary state
of high energy E2 to a state of low energy E1 and in doing so, it emits
a single photon with frequency,
ν = E2−E1
h
where h is the Planck's constant.
Conversely, on absorbing an energy (E2−E1) when the electron is at
energy E1, the electron can make a transition from E1 to E2.
c. Only those orbits are allowed in the atom corresponding to which the
orbital angular momentum (L) of the electron is an integral multiple of h/
2π,
Thus,
L = nh
2 π where n = 0, 1, 2,.....
According to Griffiths (2004), the wave particle duality of electron tells us
that the electron exhibit both particle and wave nature but not
simultaneously. This dual nature was demonstrated by the famous double
slit experiment. The screen shows the interference pattern when both the
slits are open (even when single electron passes through the slit at a
time) confirming its wave nature. As soon as we try to make a
measurement by closing one slit so that we could find through which slit
the electron passes, the wave nature vanishes and particle nature comes
into picture.
Bohr’s Postulates were based on the fact that the electron is a particle
and its energy was calculated which was found to be similar to the
energy of the electron calculated using Quantum Mechanics methods
considering electron as a wave i.e.,
E = −Z2 me4
8 n2 h2 ϵ0
2
Q.M. Model of H - Atom
b. An electron can make a transition in the atom from a stationary state
of high energy E2 to a state of low energy E1 and in doing so, it emits
a single photon with frequency,
ν = E2−E1
h
where h is the Planck's constant.
Conversely, on absorbing an energy (E2−E1) when the electron is at
energy E1, the electron can make a transition from E1 to E2.
c. Only those orbits are allowed in the atom corresponding to which the
orbital angular momentum (L) of the electron is an integral multiple of h/
2π,
Thus,
L = nh
2 π where n = 0, 1, 2,.....
According to Griffiths (2004), the wave particle duality of electron tells us
that the electron exhibit both particle and wave nature but not
simultaneously. This dual nature was demonstrated by the famous double
slit experiment. The screen shows the interference pattern when both the
slits are open (even when single electron passes through the slit at a
time) confirming its wave nature. As soon as we try to make a
measurement by closing one slit so that we could find through which slit
the electron passes, the wave nature vanishes and particle nature comes
into picture.
Bohr’s Postulates were based on the fact that the electron is a particle
and its energy was calculated which was found to be similar to the
energy of the electron calculated using Quantum Mechanics methods
considering electron as a wave i.e.,
E = −Z2 me4
8 n2 h2 ϵ0
2

4
Q.M. Model of H - Atom
The wave particle duality was further backed up by deBroglie hypothesis
who claimed that every particle must be associated with a wave called
Matter Waves whose wavelength( λ) is given by the formula-
Wavelength of matter wave (λ) = h
mv
Here,
h - Planck’s Constant
m - the mass of the particle
v - velocity of the particle.
2. As stated in Griffiths (2013), according to Maxwell’s Electromagnetic
Theory, an accelerated charge particle radiate energy. Rutherford’s
classical model suggested the circular motion of the electron. Due to its
circular motion, the electron will accelerate toward the centre and thus it
will radiate energy which implies it will loose energy and its radius of
circular path will eventually get smaller and smaller resulting in the jump
of electron into the nucleus. Therefore, the atom is not stable and will
vanish after radiating all its energy of the electron. Moreover, this model
didn’t explain the various Hydrogen Spectral lines which were observed
experimentally.
Q.M. Model of H - Atom
The wave particle duality was further backed up by deBroglie hypothesis
who claimed that every particle must be associated with a wave called
Matter Waves whose wavelength( λ) is given by the formula-
Wavelength of matter wave (λ) = h
mv
Here,
h - Planck’s Constant
m - the mass of the particle
v - velocity of the particle.
2. As stated in Griffiths (2013), according to Maxwell’s Electromagnetic
Theory, an accelerated charge particle radiate energy. Rutherford’s
classical model suggested the circular motion of the electron. Due to its
circular motion, the electron will accelerate toward the centre and thus it
will radiate energy which implies it will loose energy and its radius of
circular path will eventually get smaller and smaller resulting in the jump
of electron into the nucleus. Therefore, the atom is not stable and will
vanish after radiating all its energy of the electron. Moreover, this model
didn’t explain the various Hydrogen Spectral lines which were observed
experimentally.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

5
Q.M. Model of H - Atom
Figure - 1
Bohr removed constraint of unstability of the atom and also explained the
spectra produced by Hydrogen Atom by postulating that electron revolve
in fixed orbits called Stationary Orbit of fixed orbits with fixed discrete
energy levels. According to him, an atom can only radiate energy
whenever there is a transition from a high energy level to a low energy
level. He calculated the formula for radius and velocity of the electron in
the orbit given by (Kumar, 2009),
rn = n2 ℏ2
4 π e2 me ϵ0
❑ and
v =
√ 4 π ϵ0 e2
r me
Q.M. Model of H - Atom
Figure - 1
Bohr removed constraint of unstability of the atom and also explained the
spectra produced by Hydrogen Atom by postulating that electron revolve
in fixed orbits called Stationary Orbit of fixed orbits with fixed discrete
energy levels. According to him, an atom can only radiate energy
whenever there is a transition from a high energy level to a low energy
level. He calculated the formula for radius and velocity of the electron in
the orbit given by (Kumar, 2009),
rn = n2 ℏ2
4 π e2 me ϵ0
❑ and
v =
√ 4 π ϵ0 e2
r me

6
Q.M. Model of H - Atom
Figure – 2
But Bohr’s Theory was not able to explain the atomic spectra of non-
Hydrogenic atoms. Also, it didn’t explained the spectral lines splitting on
the application of magnetic field which is nothing but Zeeman Effect. It
was later explained by the quantum mechanical model taking into
consideration the electron’s spin in the atom. (Kumar, 2018)
3. The particle nature of the electron gave simultaneous measurement
of the momentum and position of the particle. For an electron moving in
a circular orbit of Hydrogen atom, we know its radius exactly i.e., rn =
Q.M. Model of H - Atom
Figure – 2
But Bohr’s Theory was not able to explain the atomic spectra of non-
Hydrogenic atoms. Also, it didn’t explained the spectral lines splitting on
the application of magnetic field which is nothing but Zeeman Effect. It
was later explained by the quantum mechanical model taking into
consideration the electron’s spin in the atom. (Kumar, 2018)
3. The particle nature of the electron gave simultaneous measurement
of the momentum and position of the particle. For an electron moving in
a circular orbit of Hydrogen atom, we know its radius exactly i.e., rn =

7
Q.M. Model of H - Atom
4 π ℏ2 ℇ0 n2
me e2 ( Z = 1) and thus ∆r = 0. However, since it is moving in a
circular orbit, it cannot have any radial velocity, and thus pr = 0 and ∆pr =
0. Thus, we have simultaneous exact knowledge of both r and pr which
violates the uncertainty principle.(Ghoshal, 2010)
Now, considering the quantum mechanical model of Hydrogen atom i.e.,
electron in an infinite potential well, we consider electron as a wave
whose wavefuntion and energy is given by-
ψn = √ 2
L sin ( nπx
L ) n = 1, 2, 3,...
En = n2 π2 ℏ2
2 m L2 n = 1, 2, 3,....
According to Bransden and Joachan (2003), a single sinusoidal wave has a
precise measurable wavelength (λ), so the electron presented by a sine
wave which is nothing but the matter wave suggested by deBroglie has a
precise or definite momentum. But a single sine wave keeps going in
both the directions i.e., the wave is not localized anywhere. So, the
position of the electron is totally uncertain. When several sine waves
having unique wavelength each are added together, we get a resultant
wave that is localized to some extent. Adding more sine waves together
gives us more localized resultant wave , and it also gives less uncertainty
about the electron's location. It is not clear which wavelength satisfies
deBroglie's formula for the calculation of electron’s momentum, since, the
resultant wave consists of a range of wavelengths ( wavelengths of the
sinusoidal waves) existing simtaneously. Thus, this gives us uncertainty
about the electron's momentum to some extent. When more sine waves
Q.M. Model of H - Atom
4 π ℏ2 ℇ0 n2
me e2 ( Z = 1) and thus ∆r = 0. However, since it is moving in a
circular orbit, it cannot have any radial velocity, and thus pr = 0 and ∆pr =
0. Thus, we have simultaneous exact knowledge of both r and pr which
violates the uncertainty principle.(Ghoshal, 2010)
Now, considering the quantum mechanical model of Hydrogen atom i.e.,
electron in an infinite potential well, we consider electron as a wave
whose wavefuntion and energy is given by-
ψn = √ 2
L sin ( nπx
L ) n = 1, 2, 3,...
En = n2 π2 ℏ2
2 m L2 n = 1, 2, 3,....
According to Bransden and Joachan (2003), a single sinusoidal wave has a
precise measurable wavelength (λ), so the electron presented by a sine
wave which is nothing but the matter wave suggested by deBroglie has a
precise or definite momentum. But a single sine wave keeps going in
both the directions i.e., the wave is not localized anywhere. So, the
position of the electron is totally uncertain. When several sine waves
having unique wavelength each are added together, we get a resultant
wave that is localized to some extent. Adding more sine waves together
gives us more localized resultant wave , and it also gives less uncertainty
about the electron's location. It is not clear which wavelength satisfies
deBroglie's formula for the calculation of electron’s momentum, since, the
resultant wave consists of a range of wavelengths ( wavelengths of the
sinusoidal waves) existing simtaneously. Thus, this gives us uncertainty
about the electron's momentum to some extent. When more sine waves
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
8
Q.M. Model of H - Atom
are added to the wave, the wave after addition will give more localization
of the electron but there will also be more uncertainty in the momentum
and wavelength of the electron represented by the resultant wave .
Therefore, the quantum mechanical model satisfies the Heisenberg
uncertainty principle.
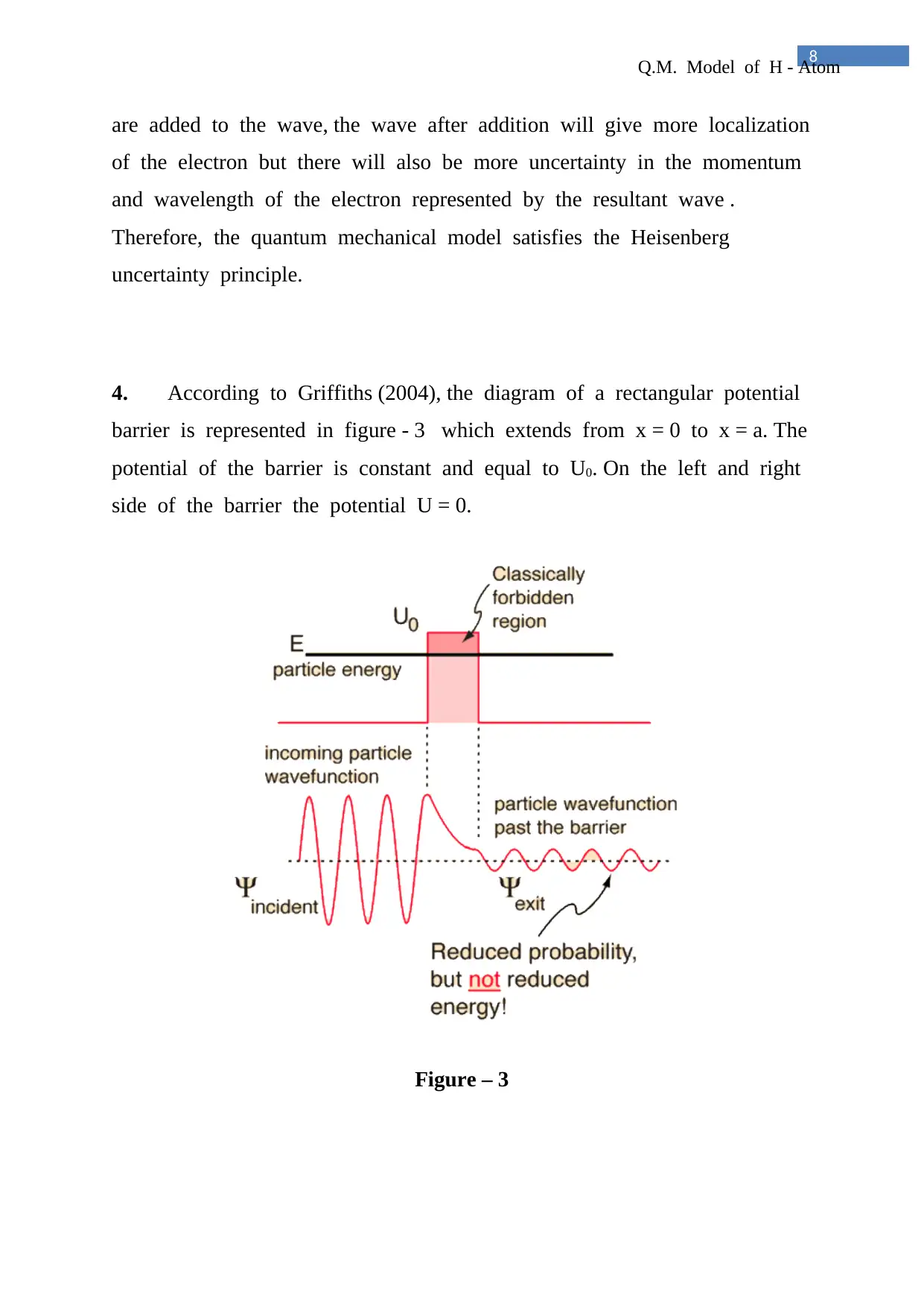
4. According to Griffiths (2004), the diagram of a rectangular potential
barrier is represented in figure - 3 which extends from x = 0 to x = a. The
potential of the barrier is constant and equal to U0. On the left and right
side of the barrier the potential U = 0.
Figure – 3
Q.M. Model of H - Atom
are added to the wave, the wave after addition will give more localization
of the electron but there will also be more uncertainty in the momentum
and wavelength of the electron represented by the resultant wave .
Therefore, the quantum mechanical model satisfies the Heisenberg
uncertainty principle.
4. According to Griffiths (2004), the diagram of a rectangular potential
barrier is represented in figure - 3 which extends from x = 0 to x = a. The
potential of the barrier is constant and equal to U0. On the left and right
side of the barrier the potential U = 0.
Figure – 3

9
Q.M. Model of H - Atom
Considering that a stream of particles of energy E be incident from left
on the barrier surface at x = 0. The following two cases arise-
a. If E > U0, then according to classical mechanics the particles will be
wholly transmitted and no reflection is possible. But quantum
mechanically there is always some probability at x = 0 and x = a
b. If E < U0, then classically the particles will be wholly reflected and
hence penetration through the barrier is impossible. But quantum
mechanically there is always some probability of penetration into the
barrier and appearance of the particles in region III. This finite probability
of transmission through the barrier even for E < U0 is called the Quantum
Mechanical Tunnelling Effect.
After solving the Schrodinger Equation for the case E < U0 , we will find
that the transmission coefficient for the given particle to pass through the
potential barrier is given by-
T =
1
1+ U0
2 sin h2 (βa)
4 E(U 0−E)
Here, β= √ 2 m(U0 −E)
ℏ2 ; m - mass of the particle
From T ≠0 implies that there is a finite probability of transmission of the
particle through the potential barrier of height U0 and width a even if
E < U0 . This cannot be accounted for in view of classical theory.
Transmission coefficient depends on 4 factors i.e., width of barrier (a),
mass of particle (m), Energy of the particle (E), and the barrier height (U0)
We know that mass of human beings (mhb) is much larger than the mass
of the electron (me), i.e., mhb >> me. . So, in case of humans, m →large
value , so, βa → ∞
Q.M. Model of H - Atom
Considering that a stream of particles of energy E be incident from left
on the barrier surface at x = 0. The following two cases arise-
a. If E > U0, then according to classical mechanics the particles will be
wholly transmitted and no reflection is possible. But quantum
mechanically there is always some probability at x = 0 and x = a
b. If E < U0, then classically the particles will be wholly reflected and
hence penetration through the barrier is impossible. But quantum
mechanically there is always some probability of penetration into the
barrier and appearance of the particles in region III. This finite probability
of transmission through the barrier even for E < U0 is called the Quantum
Mechanical Tunnelling Effect.
After solving the Schrodinger Equation for the case E < U0 , we will find
that the transmission coefficient for the given particle to pass through the
potential barrier is given by-
T =
1
1+ U0
2 sin h2 (βa)
4 E(U 0−E)
Here, β= √ 2 m(U0 −E)
ℏ2 ; m - mass of the particle
From T ≠0 implies that there is a finite probability of transmission of the
particle through the potential barrier of height U0 and width a even if
E < U0 . This cannot be accounted for in view of classical theory.
Transmission coefficient depends on 4 factors i.e., width of barrier (a),
mass of particle (m), Energy of the particle (E), and the barrier height (U0)
We know that mass of human beings (mhb) is much larger than the mass
of the electron (me), i.e., mhb >> me. . So, in case of humans, m →large
value , so, βa → ∞

10
Q.M. Model of H - Atom
∴ sinh2(βa) = ( eβa−e− βa
2 )
2
= e2 βa
4 >> 1
∴ T = 16(U0 −E)
U 0
2 e−2 βa
which will be nearly zero for βa → ∞
While for electron, it the wavefunction will retain its amplitude even after
penetrating a small barrier.
Hence, electrons can do quantum tunnel through potential barriers yet we
cannot.
Conclusion
The spectacular discovery of dual nature of electron gave rise to a new
field of Physics called Quantum Mechanics. Many complex problems of
the nature could be solved now using quantum techniques. One thing that
should be kept in mind that the quantum mechanics is applicable only for
very small particles like proton, electron, etc. Quantum Mechanics gives us
probabilistic results unlike the Newtonian mechanics. Numerous technology
have been given using this new field of science like Scanning Tunnelling
Microscope which uses tunnelling effect of the electron, Quantum Dots
and Quantum Computations and many more. In the end , we can
conclude that the riddle of the structure of atoms is successfully
explained with the help of Quantum Mechanics.
References
Q.M. Model of H - Atom
∴ sinh2(βa) = ( eβa−e− βa
2 )
2
= e2 βa
4 >> 1
∴ T = 16(U0 −E)
U 0
2 e−2 βa
which will be nearly zero for βa → ∞
While for electron, it the wavefunction will retain its amplitude even after
penetrating a small barrier.
Hence, electrons can do quantum tunnel through potential barriers yet we
cannot.
Conclusion
The spectacular discovery of dual nature of electron gave rise to a new
field of Physics called Quantum Mechanics. Many complex problems of
the nature could be solved now using quantum techniques. One thing that
should be kept in mind that the quantum mechanics is applicable only for
very small particles like proton, electron, etc. Quantum Mechanics gives us
probabilistic results unlike the Newtonian mechanics. Numerous technology
have been given using this new field of science like Scanning Tunnelling
Microscope which uses tunnelling effect of the electron, Quantum Dots
and Quantum Computations and many more. In the end , we can
conclude that the riddle of the structure of atoms is successfully
explained with the help of Quantum Mechanics.
References
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

11
Q.M. Model of H - Atom
Bransden B.H. and Joachan C.J. (2003). Physics of Atoms and Molecules.
2nd Edition. London: Pearson
Friedrich H. (2006). Theoretical Atomic Physics. 3rd Edition. Berlin: Springer
Gasiorowicz S. (2007). Quantum Physics. 3rd Edition. New Jersey: Wiley
Ghoshal S.N. (2010). Atomic Physics. Delhi: S.Chand
Griffiths D.J. (2013). Introduction to Electrodynamics. 4th Edition. London:
Pearson Education
Griffiths D.J. (2004). Introduction to Quantum Mechanics. 2nd Edition.
London: Pearson Education
Kumar A. (2018). Fundamentals of Quantum Mechanics. Cambridge:
Cambridge University Press
Kumar R. (2009). Atomic and Molecular Physics. Meerut: Campus Books
Saraswati V. (2017) Quantum Mechanics Atomic and Molecular Physics.
Delhi: Himanshu Publications
Q.M. Model of H - Atom
Bransden B.H. and Joachan C.J. (2003). Physics of Atoms and Molecules.
2nd Edition. London: Pearson
Friedrich H. (2006). Theoretical Atomic Physics. 3rd Edition. Berlin: Springer
Gasiorowicz S. (2007). Quantum Physics. 3rd Edition. New Jersey: Wiley
Ghoshal S.N. (2010). Atomic Physics. Delhi: S.Chand
Griffiths D.J. (2013). Introduction to Electrodynamics. 4th Edition. London:
Pearson Education
Griffiths D.J. (2004). Introduction to Quantum Mechanics. 2nd Edition.
London: Pearson Education
Kumar A. (2018). Fundamentals of Quantum Mechanics. Cambridge:
Cambridge University Press
Kumar R. (2009). Atomic and Molecular Physics. Meerut: Campus Books
Saraswati V. (2017) Quantum Mechanics Atomic and Molecular Physics.
Delhi: Himanshu Publications
1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.
