BSB123 Data Analysis: Statistical Analysis of GPA Influencers
VerifiedAdded on 2023/06/03
|7
|1649
|219
Report
AI Summary
This report investigates the factors influencing the Grade Point Average (GPA) of science students, focusing on socioeconomic status (SES), gender, high school scores, and ATAR. T-tests reveal no significant GPA difference between students with postgraduate or undergraduate educated parents but a significant difference between those with undergraduate versus secondary-level educated parents. Gender showed no significant impact. Stepwise regression indicates that high school science scores are not strong GPA predictors, and ATAR does not improve the model fit. The recommended model includes high school scores in science, English, and math, explaining 23.5% of GPA variations, suggesting other unexamined factors also play a role. Desklib provides access to similar reports and study tools for students.

1
BSB123 Data Analysis
Assessment Item 2: Research Report
Task 1: Boxplot and t-tests
1. a) The chart below shows the side-by side boxplot of GPA for male and female. It is
evident that the average GPA score for female science students is slightly higher than that
of male science students. The chart also indicates the score for both groups are
symmetrically distributed. However, male students have a large variability than the
female students.
b) we use the t-test because the variance is unknown. The hypotheses to be testes are
stated as:
Null hypothesis: There is no significant difference in GPA on average between male and female
students in the Science Department
Alternative hypothesis: There is significant difference in GPA on average between male and
female students in the Science Department
The t-test results are shown in the table below.
t-Test: Two-Sample Assuming Unequal Variances
Male GPA Female GPA
Mean 4.52 4.75
Variance 1.97 1.40
Observations 145 79
BSB123 Data Analysis
Assessment Item 2: Research Report
Task 1: Boxplot and t-tests
1. a) The chart below shows the side-by side boxplot of GPA for male and female. It is
evident that the average GPA score for female science students is slightly higher than that
of male science students. The chart also indicates the score for both groups are
symmetrically distributed. However, male students have a large variability than the
female students.
b) we use the t-test because the variance is unknown. The hypotheses to be testes are
stated as:
Null hypothesis: There is no significant difference in GPA on average between male and female
students in the Science Department
Alternative hypothesis: There is significant difference in GPA on average between male and
female students in the Science Department
The t-test results are shown in the table below.
t-Test: Two-Sample Assuming Unequal Variances
Male GPA Female GPA
Mean 4.52 4.75
Variance 1.97 1.40
Observations 145 79
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

2
Hypothesized Mean Difference 0
df 184
t Stat -1.2941
P(T<=t) one-tail 0.0986
t Critical one-tail 1.6532
P(T<=t) two-tail 0.1972
t Critical two-tail 1.9729
The p-value = 0.1972 is larger than 0.05, the level of significance. Hence, we fail to reject the
null hypothesis. We can conclude that there is no significant difference in GPA on average
between male and female students in the Science Department at 95% confidence level.
2. (a) This a right one-tailed test. The t-score = 0.9396, and the p-value = 0.1757 which is
larger than 0.05, the level of significance. We conclude that there is no statistically
significant evidence to support the hypothesis. Therefore, at 5% level of significance,
students whose parents have a post-graduate qualification do not have higher GPA than
students whose parents have only an undergraduate qualification.
t-Test: Two-Sample Assuming Unequal Variances
GPA_Postgrad GPA_Undergad
Mean 5.10 4.89
Variance 1.24 1.57
Observations 32 105
Hypothesized Mean Difference 0
df 57
t Stat 0.9396
P(T<=t) one-tail 0.1757
t Critical one-tail 1.6720
P(T<=t) two-tail 0.3514
t Critical two-tail 2.0025
(b) The t-score = 4.2908, and the p-value = 0.00 which is less than 0.05, the level of
significance. We conclude that there is statistically significant evidence to support the
hypothesis. Therefore, at 5% level of significance, students whose parents have an
undergraduate qualification have higher GPA than students whose parents have only a
secondary or below qualification.
t-Test: Two-Sample Assuming Unequal Variances
GPA_Undergad GPA_Secondary
Mean 4.89 4.08
Variance 1.57 1.79
Observations 105 87
Hypothesized Mean Difference 0
Hypothesized Mean Difference 0
df 184
t Stat -1.2941
P(T<=t) one-tail 0.0986
t Critical one-tail 1.6532
P(T<=t) two-tail 0.1972
t Critical two-tail 1.9729
The p-value = 0.1972 is larger than 0.05, the level of significance. Hence, we fail to reject the
null hypothesis. We can conclude that there is no significant difference in GPA on average
between male and female students in the Science Department at 95% confidence level.
2. (a) This a right one-tailed test. The t-score = 0.9396, and the p-value = 0.1757 which is
larger than 0.05, the level of significance. We conclude that there is no statistically
significant evidence to support the hypothesis. Therefore, at 5% level of significance,
students whose parents have a post-graduate qualification do not have higher GPA than
students whose parents have only an undergraduate qualification.
t-Test: Two-Sample Assuming Unequal Variances
GPA_Postgrad GPA_Undergad
Mean 5.10 4.89
Variance 1.24 1.57
Observations 32 105
Hypothesized Mean Difference 0
df 57
t Stat 0.9396
P(T<=t) one-tail 0.1757
t Critical one-tail 1.6720
P(T<=t) two-tail 0.3514
t Critical two-tail 2.0025
(b) The t-score = 4.2908, and the p-value = 0.00 which is less than 0.05, the level of
significance. We conclude that there is statistically significant evidence to support the
hypothesis. Therefore, at 5% level of significance, students whose parents have an
undergraduate qualification have higher GPA than students whose parents have only a
secondary or below qualification.
t-Test: Two-Sample Assuming Unequal Variances
GPA_Undergad GPA_Secondary
Mean 4.89 4.08
Variance 1.57 1.79
Observations 105 87
Hypothesized Mean Difference 0
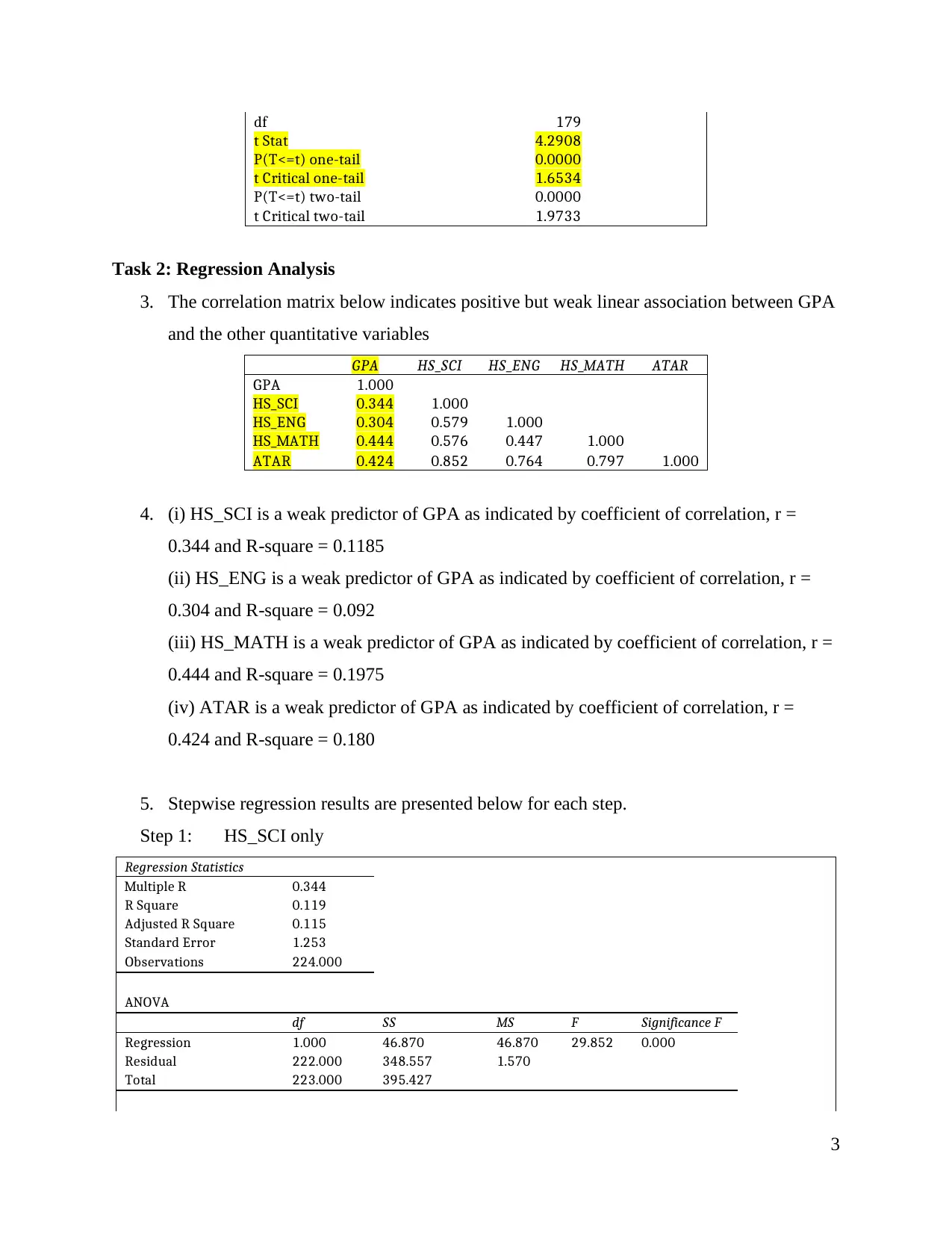
3
df 179
t Stat 4.2908
P(T<=t) one-tail 0.0000
t Critical one-tail 1.6534
P(T<=t) two-tail 0.0000
t Critical two-tail 1.9733
Task 2: Regression Analysis
3. The correlation matrix below indicates positive but weak linear association between GPA
and the other quantitative variables
GPA HS_SCI HS_ENG HS_MATH ATAR
GPA 1.000
HS_SCI 0.344 1.000
HS_ENG 0.304 0.579 1.000
HS_MATH 0.444 0.576 0.447 1.000
ATAR 0.424 0.852 0.764 0.797 1.000
4. (i) HS_SCI is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.344 and R-square = 0.1185
(ii) HS_ENG is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.304 and R-square = 0.092
(iii) HS_MATH is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.444 and R-square = 0.1975
(iv) ATAR is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.424 and R-square = 0.180
5. Stepwise regression results are presented below for each step.
Step 1: HS_SCI only
Regression Statistics
Multiple R 0.344
R Square 0.119
Adjusted R Square 0.115
Standard Error 1.253
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 1.000 46.870 46.870 29.852 0.000
Residual 222.000 348.557 1.570
Total 223.000 395.427
df 179
t Stat 4.2908
P(T<=t) one-tail 0.0000
t Critical one-tail 1.6534
P(T<=t) two-tail 0.0000
t Critical two-tail 1.9733
Task 2: Regression Analysis
3. The correlation matrix below indicates positive but weak linear association between GPA
and the other quantitative variables
GPA HS_SCI HS_ENG HS_MATH ATAR
GPA 1.000
HS_SCI 0.344 1.000
HS_ENG 0.304 0.579 1.000
HS_MATH 0.444 0.576 0.447 1.000
ATAR 0.424 0.852 0.764 0.797 1.000
4. (i) HS_SCI is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.344 and R-square = 0.1185
(ii) HS_ENG is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.304 and R-square = 0.092
(iii) HS_MATH is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.444 and R-square = 0.1975
(iv) ATAR is a weak predictor of GPA as indicated by coefficient of correlation, r =
0.424 and R-square = 0.180
5. Stepwise regression results are presented below for each step.
Step 1: HS_SCI only
Regression Statistics
Multiple R 0.344
R Square 0.119
Adjusted R Square 0.115
Standard Error 1.253
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 1.000 46.870 46.870 29.852 0.000
Residual 222.000 348.557 1.570
Total 223.000 395.427
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
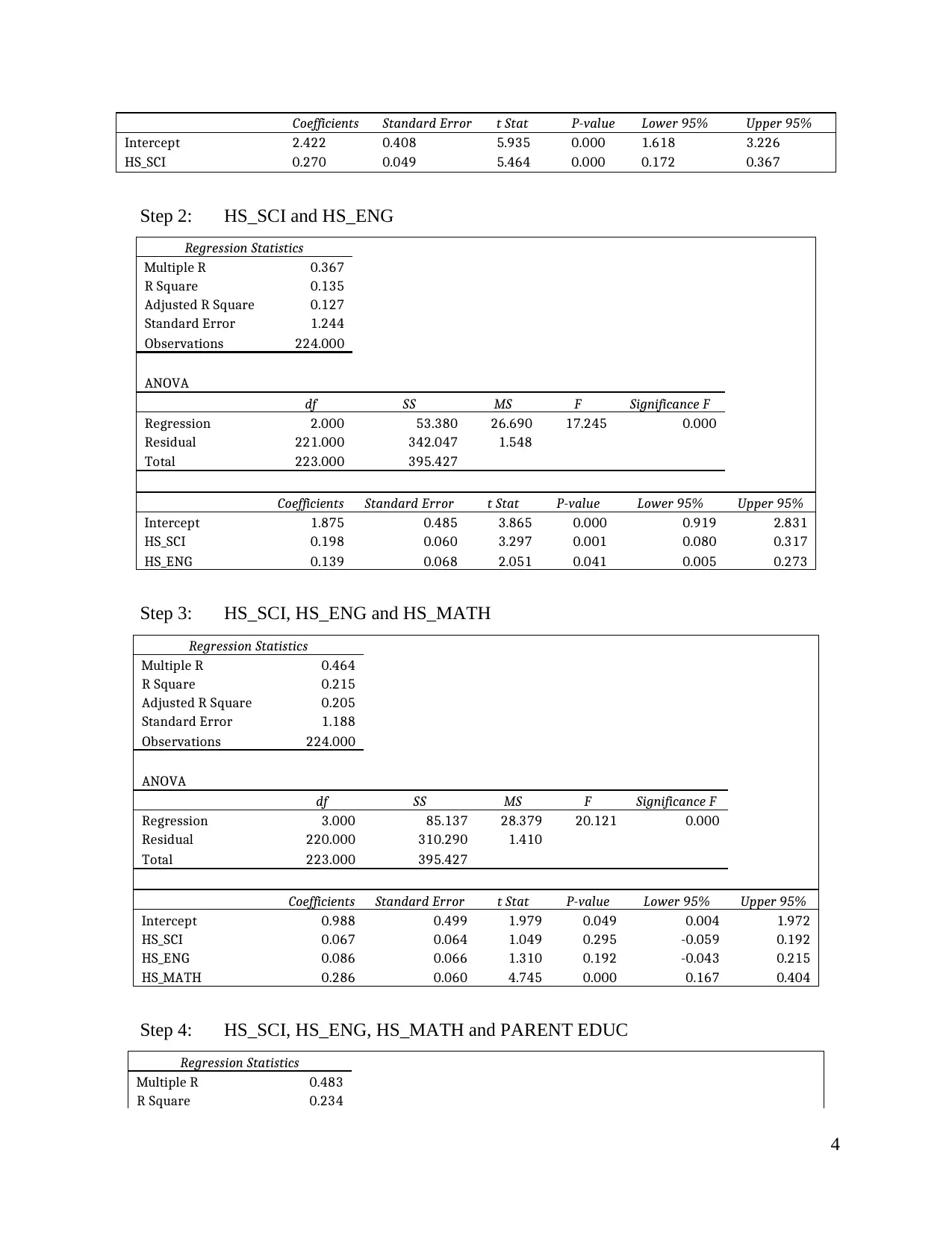
4
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 2.422 0.408 5.935 0.000 1.618 3.226
HS_SCI 0.270 0.049 5.464 0.000 0.172 0.367
Step 2: HS_SCI and HS_ENG
Regression Statistics
Multiple R 0.367
R Square 0.135
Adjusted R Square 0.127
Standard Error 1.244
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 2.000 53.380 26.690 17.245 0.000
Residual 221.000 342.047 1.548
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.875 0.485 3.865 0.000 0.919 2.831
HS_SCI 0.198 0.060 3.297 0.001 0.080 0.317
HS_ENG 0.139 0.068 2.051 0.041 0.005 0.273
Step 3: HS_SCI, HS_ENG and HS_MATH
Regression Statistics
Multiple R 0.464
R Square 0.215
Adjusted R Square 0.205
Standard Error 1.188
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 3.000 85.137 28.379 20.121 0.000
Residual 220.000 310.290 1.410
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 0.988 0.499 1.979 0.049 0.004 1.972
HS_SCI 0.067 0.064 1.049 0.295 -0.059 0.192
HS_ENG 0.086 0.066 1.310 0.192 -0.043 0.215
HS_MATH 0.286 0.060 4.745 0.000 0.167 0.404
Step 4: HS_SCI, HS_ENG, HS_MATH and PARENT EDUC
Regression Statistics
Multiple R 0.483
R Square 0.234
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 2.422 0.408 5.935 0.000 1.618 3.226
HS_SCI 0.270 0.049 5.464 0.000 0.172 0.367
Step 2: HS_SCI and HS_ENG
Regression Statistics
Multiple R 0.367
R Square 0.135
Adjusted R Square 0.127
Standard Error 1.244
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 2.000 53.380 26.690 17.245 0.000
Residual 221.000 342.047 1.548
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.875 0.485 3.865 0.000 0.919 2.831
HS_SCI 0.198 0.060 3.297 0.001 0.080 0.317
HS_ENG 0.139 0.068 2.051 0.041 0.005 0.273
Step 3: HS_SCI, HS_ENG and HS_MATH
Regression Statistics
Multiple R 0.464
R Square 0.215
Adjusted R Square 0.205
Standard Error 1.188
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 3.000 85.137 28.379 20.121 0.000
Residual 220.000 310.290 1.410
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 0.988 0.499 1.979 0.049 0.004 1.972
HS_SCI 0.067 0.064 1.049 0.295 -0.059 0.192
HS_ENG 0.086 0.066 1.310 0.192 -0.043 0.215
HS_MATH 0.286 0.060 4.745 0.000 0.167 0.404
Step 4: HS_SCI, HS_ENG, HS_MATH and PARENT EDUC
Regression Statistics
Multiple R 0.483
R Square 0.234
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
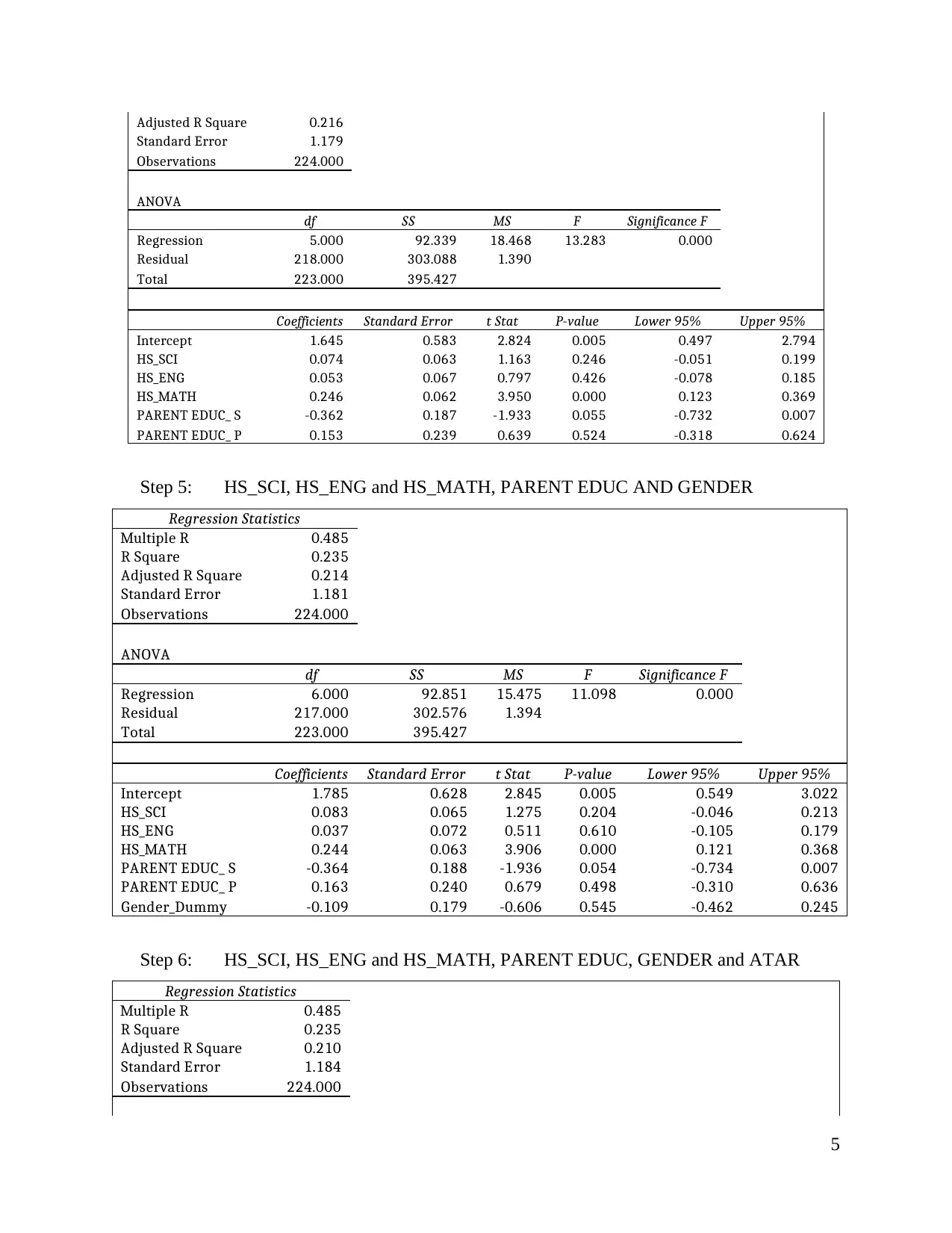
5
Adjusted R Square 0.216
Standard Error 1.179
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 5.000 92.339 18.468 13.283 0.000
Residual 218.000 303.088 1.390
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.645 0.583 2.824 0.005 0.497 2.794
HS_SCI 0.074 0.063 1.163 0.246 -0.051 0.199
HS_ENG 0.053 0.067 0.797 0.426 -0.078 0.185
HS_MATH 0.246 0.062 3.950 0.000 0.123 0.369
PARENT EDUC_ S -0.362 0.187 -1.933 0.055 -0.732 0.007
PARENT EDUC_ P 0.153 0.239 0.639 0.524 -0.318 0.624
Step 5: HS_SCI, HS_ENG and HS_MATH, PARENT EDUC AND GENDER
Regression Statistics
Multiple R 0.485
R Square 0.235
Adjusted R Square 0.214
Standard Error 1.181
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 6.000 92.851 15.475 11.098 0.000
Residual 217.000 302.576 1.394
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.785 0.628 2.845 0.005 0.549 3.022
HS_SCI 0.083 0.065 1.275 0.204 -0.046 0.213
HS_ENG 0.037 0.072 0.511 0.610 -0.105 0.179
HS_MATH 0.244 0.063 3.906 0.000 0.121 0.368
PARENT EDUC_ S -0.364 0.188 -1.936 0.054 -0.734 0.007
PARENT EDUC_ P 0.163 0.240 0.679 0.498 -0.310 0.636
Gender_Dummy -0.109 0.179 -0.606 0.545 -0.462 0.245
Step 6: HS_SCI, HS_ENG and HS_MATH, PARENT EDUC, GENDER and ATAR
Regression Statistics
Multiple R 0.485
R Square 0.235
Adjusted R Square 0.210
Standard Error 1.184
Observations 224.000
Adjusted R Square 0.216
Standard Error 1.179
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 5.000 92.339 18.468 13.283 0.000
Residual 218.000 303.088 1.390
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.645 0.583 2.824 0.005 0.497 2.794
HS_SCI 0.074 0.063 1.163 0.246 -0.051 0.199
HS_ENG 0.053 0.067 0.797 0.426 -0.078 0.185
HS_MATH 0.246 0.062 3.950 0.000 0.123 0.369
PARENT EDUC_ S -0.362 0.187 -1.933 0.055 -0.732 0.007
PARENT EDUC_ P 0.153 0.239 0.639 0.524 -0.318 0.624
Step 5: HS_SCI, HS_ENG and HS_MATH, PARENT EDUC AND GENDER
Regression Statistics
Multiple R 0.485
R Square 0.235
Adjusted R Square 0.214
Standard Error 1.181
Observations 224.000
ANOVA
df SS MS F Significance F
Regression 6.000 92.851 15.475 11.098 0.000
Residual 217.000 302.576 1.394
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.785 0.628 2.845 0.005 0.549 3.022
HS_SCI 0.083 0.065 1.275 0.204 -0.046 0.213
HS_ENG 0.037 0.072 0.511 0.610 -0.105 0.179
HS_MATH 0.244 0.063 3.906 0.000 0.121 0.368
PARENT EDUC_ S -0.364 0.188 -1.936 0.054 -0.734 0.007
PARENT EDUC_ P 0.163 0.240 0.679 0.498 -0.310 0.636
Gender_Dummy -0.109 0.179 -0.606 0.545 -0.462 0.245
Step 6: HS_SCI, HS_ENG and HS_MATH, PARENT EDUC, GENDER and ATAR
Regression Statistics
Multiple R 0.485
R Square 0.235
Adjusted R Square 0.210
Standard Error 1.184
Observations 224.000
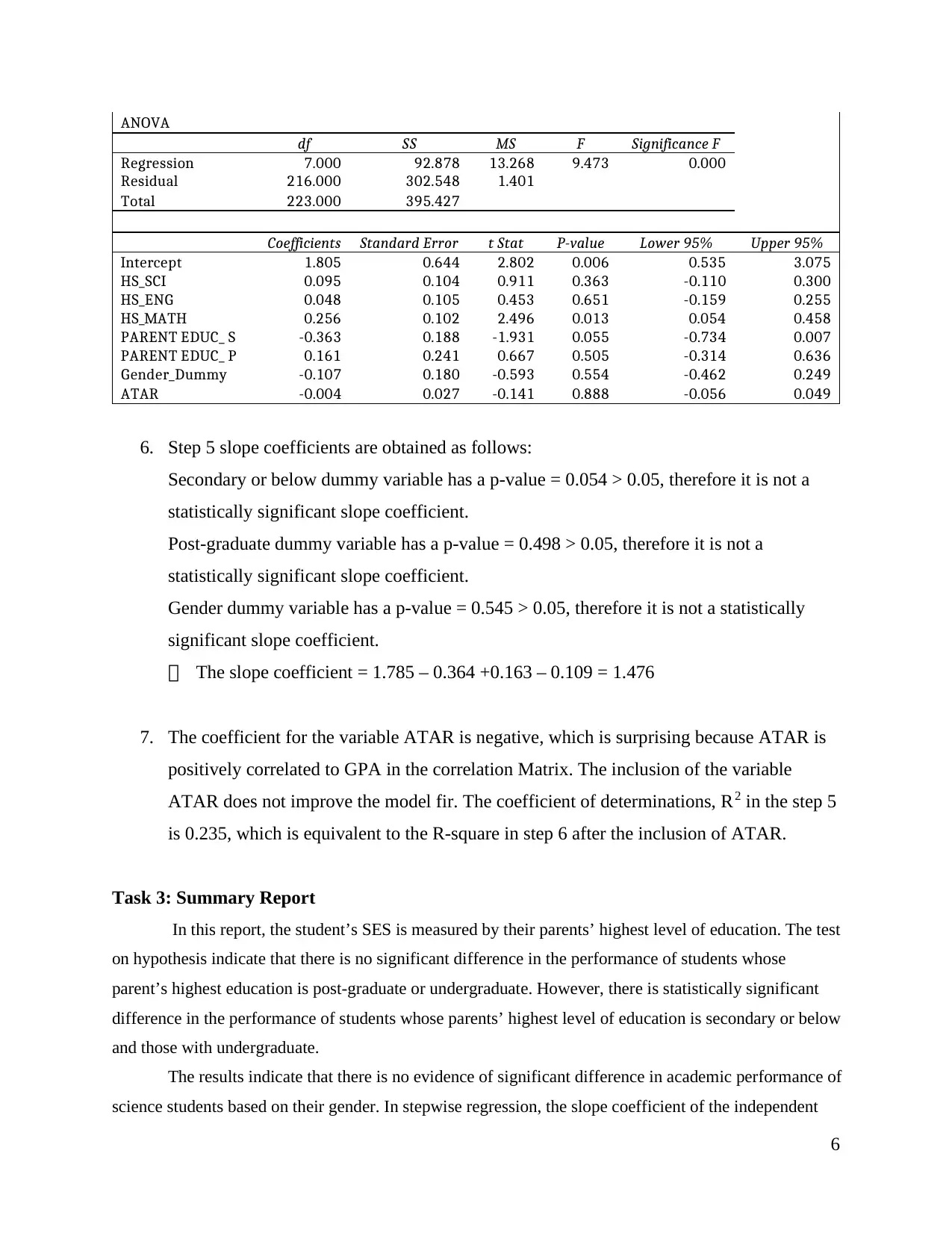
6
ANOVA
df SS MS F Significance F
Regression 7.000 92.878 13.268 9.473 0.000
Residual 216.000 302.548 1.401
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.805 0.644 2.802 0.006 0.535 3.075
HS_SCI 0.095 0.104 0.911 0.363 -0.110 0.300
HS_ENG 0.048 0.105 0.453 0.651 -0.159 0.255
HS_MATH 0.256 0.102 2.496 0.013 0.054 0.458
PARENT EDUC_ S -0.363 0.188 -1.931 0.055 -0.734 0.007
PARENT EDUC_ P 0.161 0.241 0.667 0.505 -0.314 0.636
Gender_Dummy -0.107 0.180 -0.593 0.554 -0.462 0.249
ATAR -0.004 0.027 -0.141 0.888 -0.056 0.049
6. Step 5 slope coefficients are obtained as follows:
Secondary or below dummy variable has a p-value = 0.054 > 0.05, therefore it is not a
statistically significant slope coefficient.
Post-graduate dummy variable has a p-value = 0.498 > 0.05, therefore it is not a
statistically significant slope coefficient.
Gender dummy variable has a p-value = 0.545 > 0.05, therefore it is not a statistically
significant slope coefficient.
The slope coefficient = 1.785 – 0.364 +0.163 – 0.109 = 1.476
7. The coefficient for the variable ATAR is negative, which is surprising because ATAR is
positively correlated to GPA in the correlation Matrix. The inclusion of the variable
ATAR does not improve the model fir. The coefficient of determinations, R2 in the step 5
is 0.235, which is equivalent to the R-square in step 6 after the inclusion of ATAR.
Task 3: Summary Report
In this report, the student’s SES is measured by their parents’ highest level of education. The test
on hypothesis indicate that there is no significant difference in the performance of students whose
parent’s highest education is post-graduate or undergraduate. However, there is statistically significant
difference in the performance of students whose parents’ highest level of education is secondary or below
and those with undergraduate.
The results indicate that there is no evidence of significant difference in academic performance of
science students based on their gender. In stepwise regression, the slope coefficient of the independent
ANOVA
df SS MS F Significance F
Regression 7.000 92.878 13.268 9.473 0.000
Residual 216.000 302.548 1.401
Total 223.000 395.427
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 1.805 0.644 2.802 0.006 0.535 3.075
HS_SCI 0.095 0.104 0.911 0.363 -0.110 0.300
HS_ENG 0.048 0.105 0.453 0.651 -0.159 0.255
HS_MATH 0.256 0.102 2.496 0.013 0.054 0.458
PARENT EDUC_ S -0.363 0.188 -1.931 0.055 -0.734 0.007
PARENT EDUC_ P 0.161 0.241 0.667 0.505 -0.314 0.636
Gender_Dummy -0.107 0.180 -0.593 0.554 -0.462 0.249
ATAR -0.004 0.027 -0.141 0.888 -0.056 0.049
6. Step 5 slope coefficients are obtained as follows:
Secondary or below dummy variable has a p-value = 0.054 > 0.05, therefore it is not a
statistically significant slope coefficient.
Post-graduate dummy variable has a p-value = 0.498 > 0.05, therefore it is not a
statistically significant slope coefficient.
Gender dummy variable has a p-value = 0.545 > 0.05, therefore it is not a statistically
significant slope coefficient.
The slope coefficient = 1.785 – 0.364 +0.163 – 0.109 = 1.476
7. The coefficient for the variable ATAR is negative, which is surprising because ATAR is
positively correlated to GPA in the correlation Matrix. The inclusion of the variable
ATAR does not improve the model fir. The coefficient of determinations, R2 in the step 5
is 0.235, which is equivalent to the R-square in step 6 after the inclusion of ATAR.
Task 3: Summary Report
In this report, the student’s SES is measured by their parents’ highest level of education. The test
on hypothesis indicate that there is no significant difference in the performance of students whose
parent’s highest education is post-graduate or undergraduate. However, there is statistically significant
difference in the performance of students whose parents’ highest level of education is secondary or below
and those with undergraduate.
The results indicate that there is no evidence of significant difference in academic performance of
science students based on their gender. In stepwise regression, the slope coefficient of the independent
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

7
variable HS_SCI, decreases as other variables are added to the model. Therefore, HS_SCI is not a good
predictor of student’s GPA.
ATAR is also not a good predictor of GPA and should not be include in the regression model
because its inclusion does not improve the overall model fit. The final recommended regression model
would be: GPA = 1.476 + 0.083 HS_SCI + 0.037 HS_ENG + 0.244 HS_MATH
This model as a coefficient of correlation, r of 0.485 and the model fit, R-square = 0.235. hence,
23.5% of variations in GPA can be explainsed by the three factors. Conclusively, there other important
factors influencing academic performance that were not included in the study such as environmental
factors, student’s IQ among others.
variable HS_SCI, decreases as other variables are added to the model. Therefore, HS_SCI is not a good
predictor of student’s GPA.
ATAR is also not a good predictor of GPA and should not be include in the regression model
because its inclusion does not improve the overall model fit. The final recommended regression model
would be: GPA = 1.476 + 0.083 HS_SCI + 0.037 HS_ENG + 0.244 HS_MATH
This model as a coefficient of correlation, r of 0.485 and the model fit, R-square = 0.235. hence,
23.5% of variations in GPA can be explainsed by the three factors. Conclusively, there other important
factors influencing academic performance that were not included in the study such as environmental
factors, student’s IQ among others.
1 out of 7
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.



