Building Mathematics 1: Comprehensive Mathematical Applications

This assignment provides detailed solutions to various mathematical problems under the title Building Mathematics 1. It covers scenarios involving calculations of area, forfeits, conversions, and unit analysis. The assignment also delves into arithmetic and geometric progressions, solving logarithmic and hyperbolic equations. Furthermore, it includes statistical analysis, such as determining mode, median, interquartile range, and standard deviation from revenue data. The assignment also addresses normal distribution, replacement intervals for light bulbs, and hypothesis testing using tailed tests. Desklib is a valuable resource for students seeking similar solved assignments and study materials.

Building Mathematics
1

TABLE OF CONTENTS
Table of Contents.............................................................................................................................1
TASK 1............................................................................................................................................2
Scenario 1....................................................................................................................................2
Scenario 2....................................................................................................................................2
Scenario 3....................................................................................................................................3
TASK 2............................................................................................................................................6
Scenario 1....................................................................................................................................6
Scenario 2..................................................................................................................................10
TASK 3..........................................................................................................................................15
Scenario 1..................................................................................................................................15
Scenario 2..................................................................................................................................18
TASK 4..........................................................................................................................................21
Scenario 1..................................................................................................................................21
Scenario 2..................................................................................................................................23
Scenario 3..................................................................................................................................25
Scenario 4..................................................................................................................................26
2

TASK 1
Scenario 1
(a) Length and width of rectangle
Solution
Area = Lb = 26.5 m2
Where L is length and b is width
Given b = L – 3.2
L*(L – 3.2) = 26.5
L2 – 3.2L -265 = 0
L = { - (-3.2) +- √ [(-3.2)2- 4*1* (26.5)] } / 2*1
L = 6.99 and l = -3.79
AS L cannot be negative so neglecting negative value
Length = 6.990 m
b = 6.99-3.2 = 3.790 m
(a) Daily Forfeit
Solution
Let forfeit amount of one day is = £v and original amount of contract = £u
If there is delay of 5 days, then total amount which will be deducted from contract amount is £5v
Amount received by contract if there is delay of 5 days is expressed as:
u – 5v = £4250
Similarly, if there is 12 day delay then forfeit amount for 12 days = £12v
Amount received by contract:
u – 12v = £2120
On solving both equations:
u – 5v = £4250 (i)
u – 12v = £2120 (ii)
On subtracting both the equations we have:
7v = 2130
v = £304.28
On substituting this value in equation 1
3

u – 5(304.28) = £4250
u = £5771.4
Contract amount u = £5771.4
Forfeit v = £304.28
Scenario 2
(a) Conversions
Solution
Speed = 65 miles per hour
(i) Speed in m/s :
1 mile = 1609.344 meter
1 hour = 3600 seconds so for converting mile/hour into meter/ second * by (1609.344/3600)
65 * 0.44704 = 29.05 meter per second
(ii) Time to cover distance of 100 miles:
Solution
Time = distance/ speed
= 100/65 = 1 hour 53 minutes
For covering distance of 100 miles nearly 1 hour and 53 minutes will be needed.
(iii) Average fuel consumption = 30 miles per gallon
Solution
30 miles per gallon to litre per kilometre:
1 Mile per gallon = 2.35 litre per km
30 miles/ gallon = 30 * 2.35 = 70.5 litre / km
(iv) Fuel required for the journey in litters
Solution
Fuel required for 1 km = 70.5 litre
Total journey 100 miles = 160 km
So fuel required for journey = 11280 litre
4

(a) Unit of lift
Solution
Lift = k *V2 * A * p
A = area = m2 = [M0L2T0]
p = air density = kg / m3 = [M1L-3T0]
k is dimensionless as its constant so = [M0L0T0]
V is speed in m/second = [M0L1T-1]
So V2 = [M0L2T-2]
Lift = [M0L2T0] * [M1L-3T0] * [M0L0T0] * [M0L2T-2]
Lift = [M1L1T-2] = kg meter/ second2
Scenario 3
(1) Arithmetic sequence
Solution
b , 2b/3 , b/3 , 0 .....
Sixth term:
First term a = b
Common difference d = 2b/3 – b = - b/3
Sixth term = a + (n-1) *d
= b + 5(-b/3)
= b – 5b/3
= -2b/3
Sixth term = -2b/3
Kth term : a + (k -1) *d where a is first term and d is common difference
For given AP
Kth term = b + (k -1) *(-b/3)
20th value = 15
20th value can be find as:
b + 19 *(-b/3) = 15
so b = -2.81
Sum of first 20 values:
5

Sum = (n/2) * [2a + (n-1)*d]
On substituting values:
Sum = (20/2) * [2*(-2.81) + (20-1)*(-2.8)/3]
= 10 [-5.62 – 19b/3]
= 10/3 [-16.86 + 53.39]
= 10/3 *36.53
= 121.76
Sum of 20 terms = 121.76
(2) Geometric progression
Solution
1, 1/2 , 1/4 ....
a = 1
Formula for nth term = a * r (n-1)
n = 20 and r = 0.5
20th term = 1 * 0.5 (20-1)
20th term = 1/ 524288
(2.) Value of sum
The sum of GP up to infinite number of terms is given by formula: S = a / (1-r)
On substituting values: a = 1 and r = 0.5
Sum = 1 / (1-0.5) = 2
Thus sum is equals to 2
(3) Equations
a.) 2 log 3x + log 18x = 27
Solution
Log 18x = log (3x*6)
2 log 3x + log (3x*6) = 27
2 log 3x + log 3x + log 6 = 27
2 log 3x + log 3x = 26.22
6

3 log x = 26.22
x = 10 (27 – log 162)/3 or 183440402.7
(b) 2 ln 3x + ln 18x = 9
Solution
2 ln 3x + ln 18x = 9
Using the formula: ln (ab) = ln a + ln b
We can write ln 18x = ln3x + ln 6x
2 ln 3x + ln 3x + ln 6 = 9
2 ln 3x + ln 3x = 9 – ln 6
3ln 3x = 9 – ln 6
Using the property: ln xm = m*ln x
So 3ln 3x = ln (3x)3
ln (3x)3 = 9 – ln 6
x = e (9 – ln 162) /3 = 3.68
(c1) coshx + sinhx = 5
Solution
coshx = ex + e-x / 2
sinhx = ex - e-x / 2
[ex + e-x / 2] + [ex - e-x / 2 ] = 5
ex + e-x + ex - e-x = 5*2
2ex = 10
ex = 5
X = ln 5 = 1.60
(c2) cosh2y - sinh2y = 3
Solution
Cosh2y = e2y + e-2y / 2
Sinh2y = e2y - e-2y / 2
[e2y + e-2y / 2] - [e2y - e-2y / 2] = 3
7

e2y + e-2y - e2y + e-2y = 6
2 e-2y = 6
e-2y = 3
-2y = ln 3
Y = -0.5 ln 3
y = -0.5 ln 3 = -0.54
(c3) coshk * sinhk = 2
Solution
coshk = ek + e-k / 2
sinhk = ek - e-k / 2
[ek + e-k / 2] * [ek - e-k / 2] = 2
ek + e-k + ek - e-k = 4
2ek =4
ek = 1
k = 0.5 ln (4 + √17) = 1.19
(c4) coshM / sinhM = 2
Solution
[eM + e-M / 2] / [eM - e-M / 2 ] = 2
X = 0.5 ln 3 = 0.54
TASK 2
Scenario 1
(a) Mode for rectangle distribution and histogram
Solution
Revenu
e
Januar
y July
8

0-5 27 22
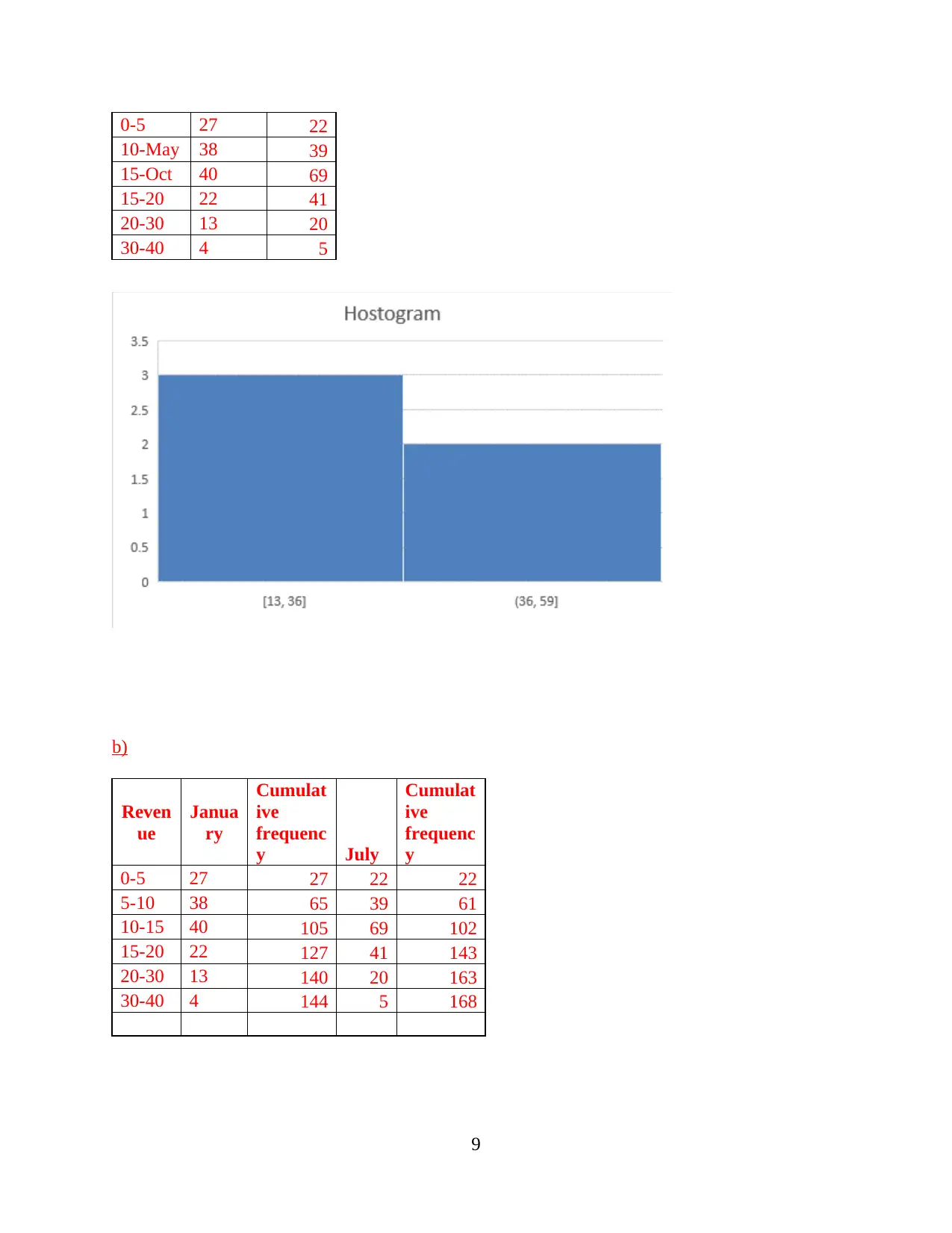
10-May 38 39
15-Oct 40 69
15-20 22 41
20-30 13 20
30-40 4 5
b)
Reven
ue
Janua
ry
Cumulat
ive
frequenc
y July
Cumulat
ive
frequenc
y
0-5 27 27 22 22
5-10 38 65 39 61
10-15 40 105 69 102
15-20 22 127 41 143
20-30 13 140 20 163
30-40 4 144 5 168
9

0-5 5-10 10-15 15-20 20-30 30-40
0
20
40
60
80
100
120
140
160
180
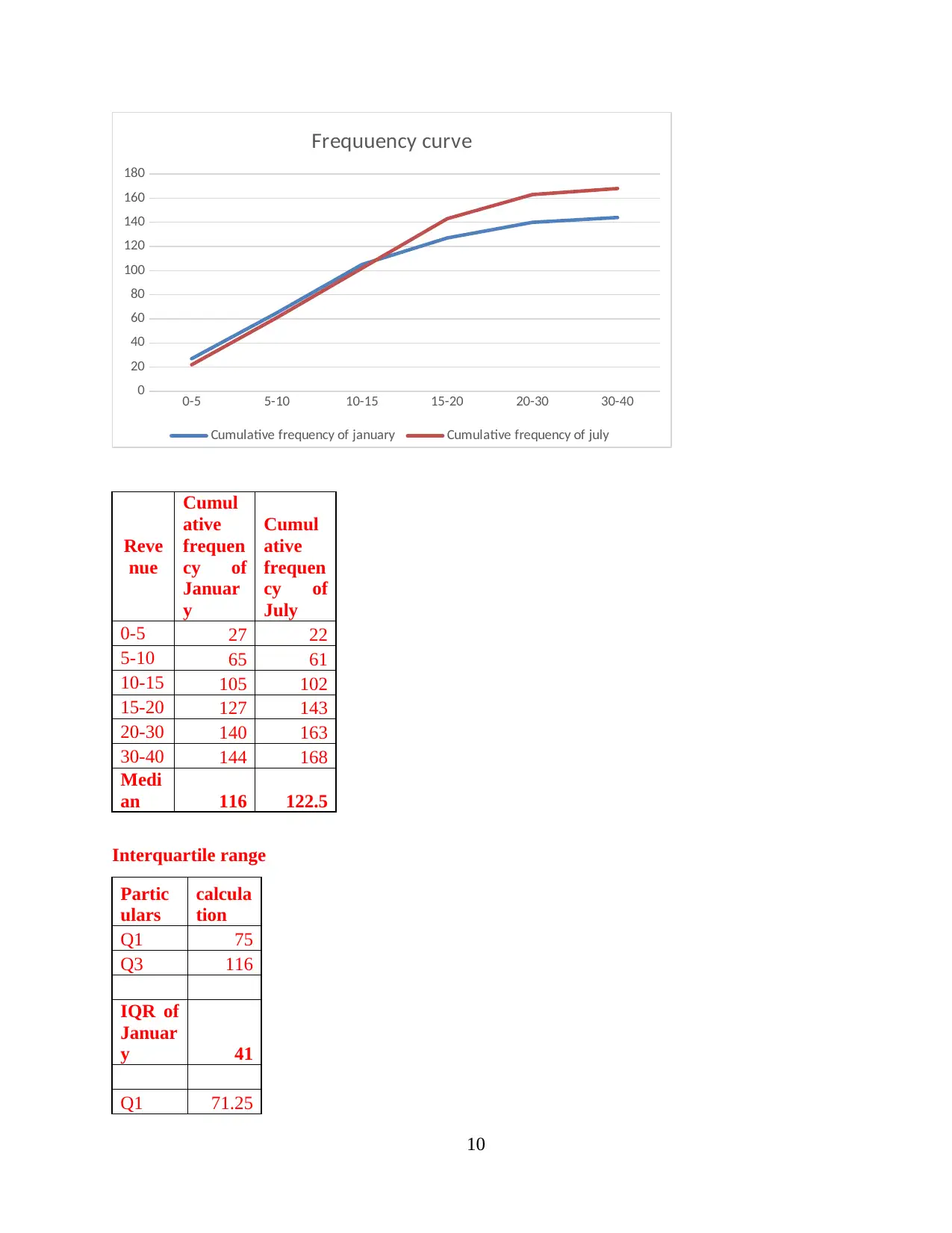
Frequuency curve
Cumulative frequency of january Cumulative frequency of july
Reve
nue
Cumul
ative
frequen
cy of
Januar
y
Cumul
ative
frequen
cy of
July
0-5 27 22
5-10 65 61
10-15 105 102
15-20 127 143
20-30 140 163
30-40 144 168
Medi
an 116 122.5
Interquartile range
Partic
ulars
calcula
tion
Q1 75
Q3 116
IQR of
Januar
y 41
Q1 71.25
10

Q3 122.5
IQR of
July 51.25
c)
Reven
ue
Januar
y
July
0-5 27 22
5-10 38 39
10-15 40 69
15-20 22 41
20-30 13 20
30-40 4 5
Mean 24 32.666
67
Range 36 64
SD 14.042
79
22.223
11
Scenario 2
(A)
Total bulbs: 5000
Mean = 360 days
Standard deviation = 60 days
(a) Normal distribution for bulb life
Solution
Normal distribution is assumed for bulb life which is tested using normality test. Its mean value
is zero and has symmetric bell shaped. The standard deviation for the curve is equals to 1. In
11

normal distribution Kurtosis range value is between +7 and -7 while that of skewness range is
given as +2 and -2. On plotting Q-Q plot using both observed and expected value it is seen that
values varying through straight line denotes false assumption and is not representing normal
distribution otherwise it has normal distribution.
(b) Replacement interval
Solution
As given only maximum of 10% bulbs can be permitted to fail prior replacement
Mean and standard deviation values are given as 360 and 60 days respectively.
As per z sore the finalised interval is 0.10. It underlines on -1.28. Hence
Expected time interval of replacement is:
(t-360) / 60 = -1.28 where t represents number of days for replacement
Thus t = 283.2 days
c.) Practical consideration influencing replacement
Solution
12

CGL policies provide coverage for property damage as well as exposure. Thus there must
be stable and regular electrical supply so that the essential measures for uninterrupted supply as
well as testing can be implemented. Along with this it is also required that there must e sufficient
number of products for test. In the given case for justifying the expected outcomes z score has
been utilised.
d.) Replacement time for type B bulbs
Solution
Mean life time: 450 days
Standard deviation: 60 days
Thus replacement time t can be calculated as:
-1.28 = (t-450) / 60
So t = 373.2 days
e.) Preference based comparison for both types of bulbs
Solution
There has been increment in cost of type A bulb. Type A bulb has mean life time of 360
days and replacement time is 283 days. On the other hand for type B bulb mean life time is 450
and replacement time is 373.2 days. So impact is 31.87%. Thus it can be said that cost increase
of 25% is not preferable because it increases by 31 days and thus average replacement must be of
360 days and standard deviation of 60 days will have less than 10%.
f.) Type C bulb replacement time
Solution
Mean: 432 days
Standard deviation: 45 days
Replacement time is for bulb C is: t
-1.28 = (t- 432) / 45
t= 489.60 days
As compare to replacement time of bulb A (283 days), replacement type of bulb C is 489.6 and
its impact is 73%
13

Hence among all three bulbs of Epiphyte engineering most preferred bulb is type C because its
standard deviation is decreasing. 73% change shows that it has better suitability for adaptation.
B.) Hypothesis testing using tailed test
Solution
Size of population is: n = 10
Average age = 27
Variance: 20
Significance level: 0.5
Assumptions: It is assumed that for this purpose simple random sampling is chosen and
population is distributed normally.
Hypothesis:
Null hypothesis H0: Average age is equals to 30
Alternative hypothesis H1: Average age is not equals to 30
Test statistic
Implication of z test statistic:
Test statistic distribution:
If chosen assumptions are valid then null hypothesis is true and standard normal
distribution is followed by statistics. Calculation for z score and hypothesis testing is as follows:
Decision rule:
14

z value in rejection zone is known as reject null hypothesis and if it lies in non-rejection zone
then it is known as failure to reject null hypothesis. As null hypothesis has structure of bell shape
it permits two tail tests.
For z<= -1.96 or z>= 1.96 rejection of null hypothesis is done.
Calculation of test statistic:
z = [27-30] / √(20/10)
z = -2.12
Statistial decision
Null hypothesis is rejected because z = -2.12 lies in rejection level because this value is
considerable at 0.05 level.
Conclusion
From above it can be concluded taht mean is not equal to 30 and P value is equals to
0.0340.
Also value of z = -2.12 represents area of 1.7% as in two tail test there are two parts of rejection
zone. However p value is double of 3.4%.
One tail test
mean age : 27 n : 10 variance : 20
Standard deviatio = 0.5
Assumptions:
 Population is normally distributed and random sampling is followed
Hypothesis
H0: =30
H1: not equals to 30
Test statistic:
Decision rule and distribution of test static
Null hypothesis is true when assmption is ture and statistic has normal distribution.
15

Significance level is 0.05 and complete rejection zone lies on left side. It shows critical value =
1.645. Rejecting null hypothesis is z < -1.645
Calculation
z = [27-30] / √(20/10)
z = -2.12
Statistical decision
Since -1.645> -2.12 so null hypothesis H0 is rejected.
Thus it can be said that p = 0.0170 and < 30 because it is one tail test.
TASK 3
Scenario 1
1.) Phase, amplitude and frequency
Solution
x1 = 3.75 sin (100π t+ 2π/9)
The equation of wave can be represented as:
A sin (Wt + ɵ)
Where A denotes amplitude of wave
W is angular frequency and ɵ is the phase shift
On comparing 3.75 sin (100π t+ 2π/9) with A sin (Wt + ɵ) we have:
Amplitude A: 3.75
16

Phase shift ɵ: 2π/9
Frequency f and periodic time t can be calculated using angular frequency:
Angular frequency W = 100π
W = 2πf
So 2πf = 100π
f = 100 /2 = 50
Frequency f = 50 Hz
Periodic time t = 1/f
= 1 / 50
Periodic time t = 0.02 seconds
x2 = 4.42 sin (100π t −2π/5)
On comparing with A sin (Wt + ɵ)
Amplitude A: 4.42
Phase ɵ: -2π/5
W = 2πf
So 2πf = 100π
Frequency f = 50 Hz
Periodic time t = 1/ f = 0.02 seconds
2.) Time for maximum displacement
Solution
First derivatives are used for determining maximum displacement.
x1 = 3.75 * sin (100π t+ 2π/9)
dx1 / dt = 375π * cos (100π t+ 2π/9)
Equating first derivative to zero:
cos (100π t+ 2π/9) = 0
100π t+ 2π/9 = (π/2)
t is equals to 2.7 milliseconds
Thus for producing maximum displacement x1 will take 2.7 milliseconds
17

For x2:
dx2 / dt = 442π cos (100π t −2π/5)
dx2 / dt = 0
442π cos (100π t −2π/5) = 0
t = 9 milliseconds
Thus x2 it will take 0.009 seconds for producing maximum displacement in
3.) Time period for given displacement value
Solution
x1 = 3.75 sin (100π t+ 2π/9)
On substituting x1 = -2 mm:
-2 = 3.75 sin (100π t+ 2π/9)
-0.5333333 = sin (100π t+ 2π/9)
arcsin (-0.533) = -0.56 + π
so 100π t+ 2π/9 = -0.56 + π
100π t = 1.88
t = 1.88 / 100π
t = 0.0059 milliseconds
x1 will have displacement of -2 mm at t = 0.0059 milliseconds
x2 = 4.42 sin (100π t −2π/5)
Substituting x2 = -2
-2 = 4.42 sin (100π t −2π/5)
-0.45 = sin (100π t −2π/5)
arcsin (-0.45) = 0.469
(100π t −2π/5) = -0.469
100π t = 0.78
t = 0.78/ 100π
t = 0.0025 seconds
x2 will produce -2 mm displacement at t = 2.51 milliseconds
18

4.) Compound angle formula
Solution
compound angle formula: sin (a +b) = sin a cos b + cos a sin b
x1 = 3.75 sin (100π t+ 2π/9)
3.75 sin (100π t+ 2π/9) can be written as:
3.75* [sin (100π t) cos (2π/9) + cos (100π t) sin (2π/9) ]
Substituting sin (2π/9) = 0.642 and cos (2π/9) = 0.766
x1 = 2.87 sin (100π t) + 2.40 cos (100π t)
On comparing with A sin φ + B cos φ we have:
A = 2.87 B= 2.40
Similarly
Compound angle formula: sin (a - b) = sin a cos b - cos a sin b
x2 = 4.42 sin (100π t −2π/5)
4.42 sin (100π t −2π/5) is expressed as :
4.42* [sin (100π t) cos (2π/5) - cos (100π t) sin (2π/5) ]
sin (2π/5)= 0.951 and cos (2π/5) = 0.309
x2 = 1.36 sin (100π t) – 4.20 cos (100π t)
= A sin φ - B cos φ
Thus A = 1.36 B= -4.20
5.) Form R sin(100πt + α)
Solution
x1 and x2 can be expressed as:
x1 = 2.87 sin (100π t) + 2.40 cos (100π t)
x2 = 1.36 sin (100π t) – 4.20 cos (100π t)
On adding both equations we have:
x1 + x2 = 2.87 sin (100π t) + 2.40 cos (100π t) + 1.36 sin (100π t) – 4.20 cos (100π t)
= 4.23 sin (100π t) -1.8 cos (100π t) (i)
Using the identity:
A sin φ - B cos φ = R sin (φ - α)
19

Where α = Tan^-1 [(B/A) ] and R = √ (A² + B²) and
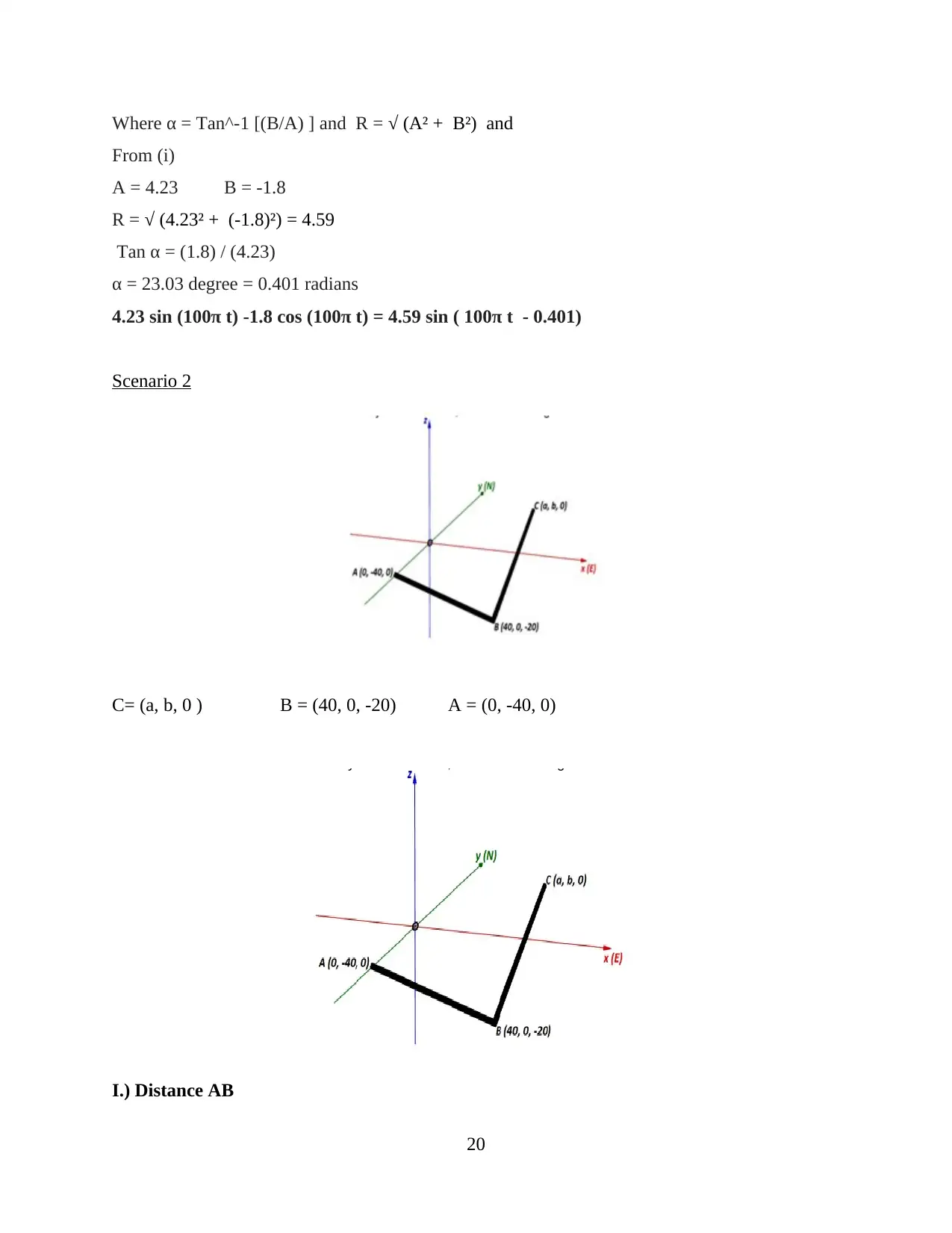
From (i)
A = 4.23 B = -1.8
R = √ (4.23² + (-1.8)²) = 4.59
Tan α = (1.8) / (4.23)
α = 23.03 degree = 0.401 radians
4.23 sin (100π t) -1.8 cos (100π t) = 4.59 sin ( 100π t - 0.401)
Scenario 2
C= (a, b, 0 ) B = (40, 0, -20) A = (0, -40, 0)
I.) Distance AB
20

Solution
Distance formula for given two coordinates P (u, v, w) Q (r, s, t) is given by formula:
PQ = √ [(r -u)² + (s -v)² + (t -w)²]
Using given formula to determine distance AB:
AB = √ [(40 -0)² + (0 -(-40))² + (-20 -0)²]
AB = 60
ii) Angle between two sections
Solution
AB = 40i + 40j – 20k
Magnitude of AB =|AB| = 60
Vector BC = 3i +4j + k
Magnitude BC =|BC| = √26
Angle formula between two vectors:
Cos φ = [(40i + 40j – 20k ). (3i +4j +k )] / [60*√26]
= 0.8498
φ = 31.81 degree
iii) Equation of vector
Solution
B= (40, 0, -20)
rho = 20
C = rho* normal vector +B
(a, b, 0 ) = 20* (3, 4, 1) + (40, 0, -20)
= (40, 0, -20) + (60, 80, 20)
So a = 100 b = 80
21

TASK 4
Scenario 1
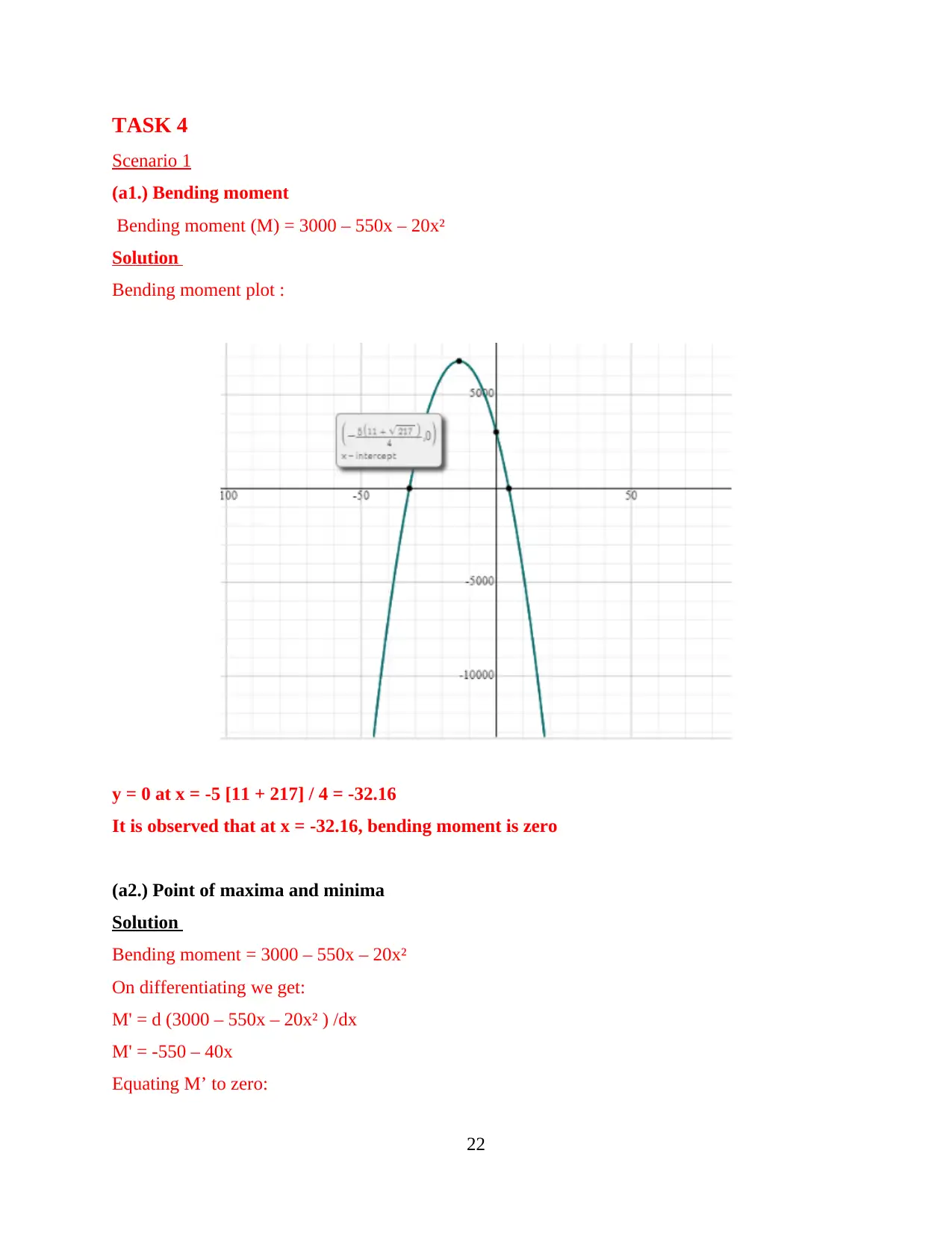
(a1.) Bending moment
Bending moment (M) = 3000 – 550x – 20x²
Solution
Bending moment plot :
y = 0 at x = -5 [11 + 217] / 4 = -32.16
It is observed that at x = -32.16, bending moment is zero
(a2.) Point of maxima and minima
Solution
Bending moment = 3000 – 550x – 20x²
On differentiating we get:
M' = d (3000 – 550x – 20x² ) /dx
M' = -550 – 40x
Equating M’ to zero:
22

-550 – 40x = 0
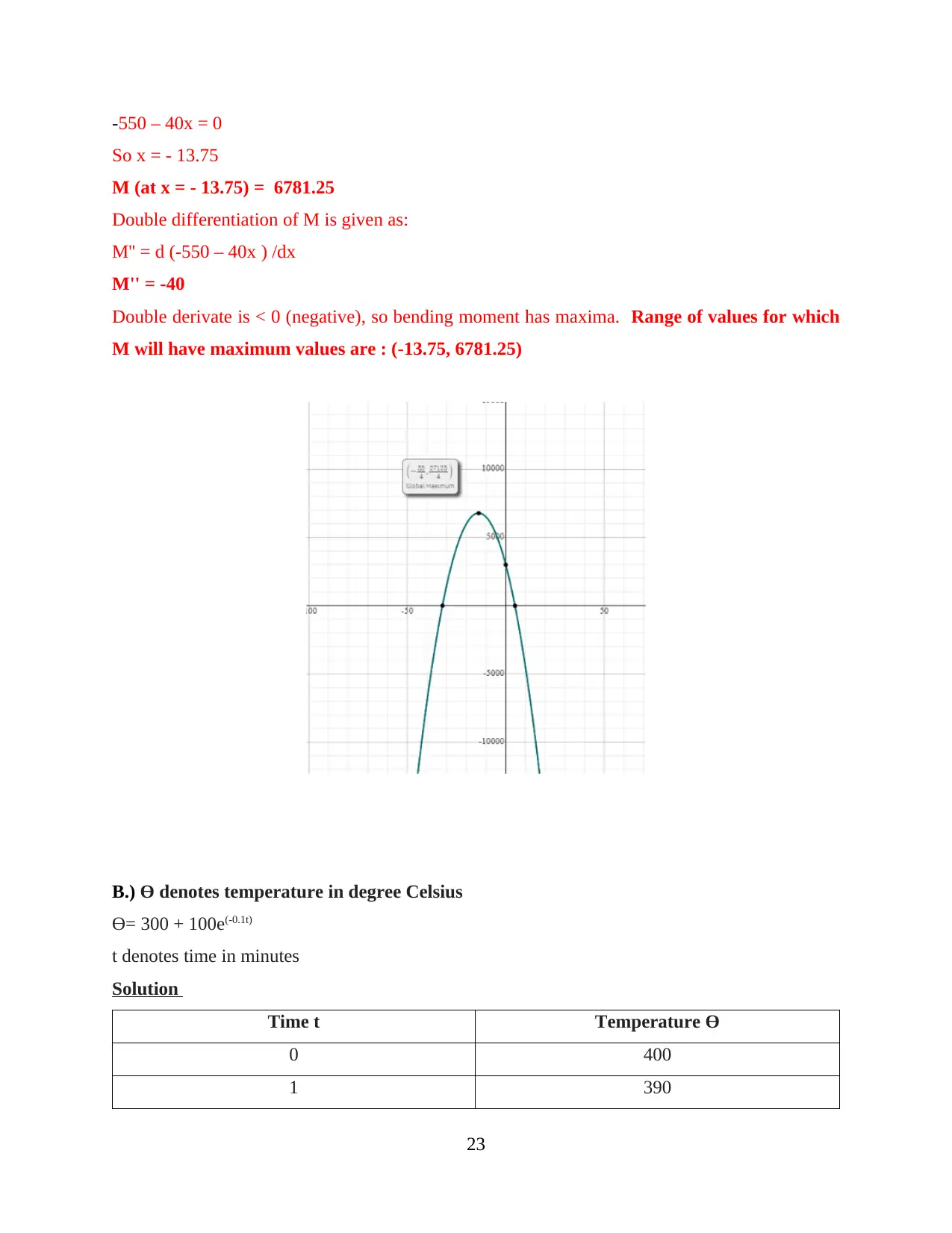
So x = - 13.75
M (at x = - 13.75) = 6781.25
Double differentiation of M is given as:
M'' = d (-550 – 40x ) /dx
M'' = -40
Double derivate is < 0 (negative), so bending moment has maxima. Range of values for which
M will have maximum values are : (-13.75, 6781.25)
B.) Ө denotes temperature in degree Celsius
Ө= 300 + 100e(-0.1t)
t denotes time in minutes
Solution
Time t Temperature Ө
0 400
1 390
23

2 381
5 360
For t > 0, temperature lies in range (400, 300) and at t = ∞ temperature will decline to 300
degree Celsius.
Ө= 300 + 100e(-0.1t)
Differentiating both the sides with respect to t
d Ө= 100 * (-0.1) e(-0.1t)
= -10 e(-0.1t)
Equating first derivative to zero we have:
d Ө= 0
-10 e(-0.1t) = 0
Thus at t = ∞ temperature will reach to its minimum value of 300.
C.) log (P) + n log (V) – log (C)
P is pressure, V denotes volume, C is constant and n denotes index
Solution
Equating the given expression to zero:
log (P) + n log (V) – log (C) = 0
log (P) + n log (V) = log (C)
Property 1: x log(y) = log (y^x)
so log (P) + log (V^n) = log (C)
Property 2: log x + log y = log (xy)
Thus:
log (PV^n) = log (C)
PV^n = C Hence proved
Determining rate of change for V
n = 2
24

Change in P at regular interval of 10 N/mm2 from 60 to 100 N/m2.
From the above relation we can write: Vn = C/P
So V = (C/P)1/n
Differentiating both the sides with respect to P
dV/dp = C / [n * P (1+n)/n]
On substituting n = 2
dV/dp = C / [2 * P (1+2)/2]
dV/dp = 0.5 * C * P-1.5
At P = 60 N/m2 V = 0.5 * (60) -1.5 = 0.00017 *C
At P = 70 N/m2 V = 0.5 * (70)-1.5 = 0.00085 *C
At P = 80 N/m2 V = 0.5 * (80) -1.5 = 0.00069 *C
At P = 90 N/m2 V = 0.5 * (90) -1.5 = 0.00058 *C
At P = 100 N/m2 V = 0.5 * (100) -1.5 = 0.0005 *C
The rate of change of V is dependent of C. Thus for two consecutive intervals C can be easily
determined. It is observed that V = √(C/P) and it represents form y =mx in which C act as rate of
change for V. Thus it can be concluded that rate of change of V = 200 as P changes.
Scenario 2
C = 16t-2 +2t-1 where C = cost and t = time.
Time range = 1 minute to 8 minute
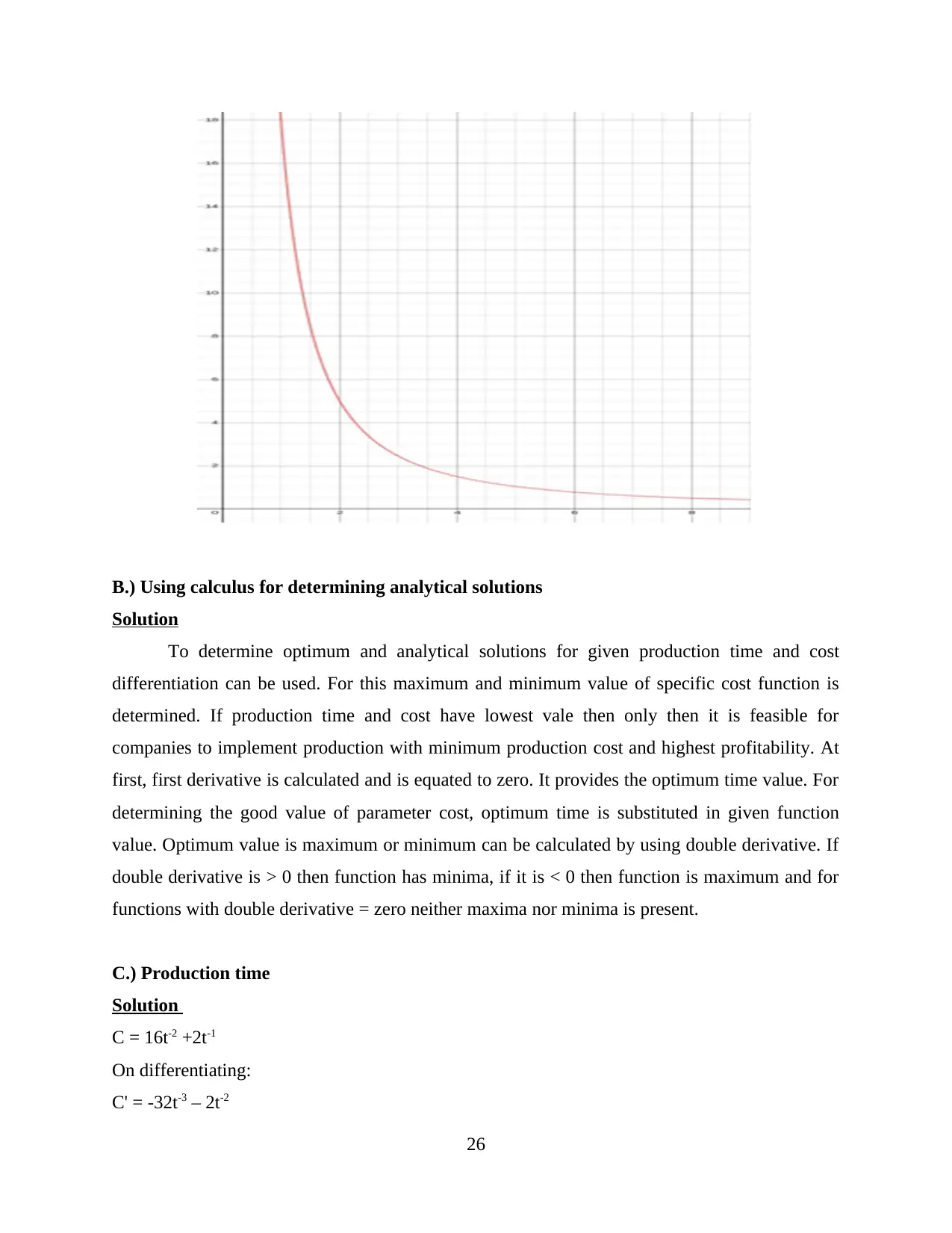
A.) Cost function over given range
Solution
Time 1 2 3 4 5 6 7 8
Cost 18 5 2.44 1.5 1.04 0.77 0.61 0.5
25

B.) Using calculus for determining analytical solutions
Solution
To determine optimum and analytical solutions for given production time and cost
differentiation can be used. For this maximum and minimum value of specific cost function is
determined. If production time and cost have lowest vale then only then it is feasible for
companies to implement production with minimum production cost and highest profitability. At
first, first derivative is calculated and is equated to zero. It provides the optimum time value. For
determining the good value of parameter cost, optimum time is substituted in given function
value. Optimum value is maximum or minimum can be calculated by using double derivative. If
double derivative is > 0 then function has minima, if it is < 0 then function is maximum and for
functions with double derivative = zero neither maxima nor minima is present.
C.) Production time
Solution
C = 16t-2 +2t-1
On differentiating:
C' = -32t-3 – 2t-2
26

Equating to zero
C' = -32t-3 – 2t-2 = 0
t = 16
Thus at t = 16 minute turning cost will be:
C = 16(16)-2 +2(16)-1
Turning cost C= 0.186 and production time = 16 minutes
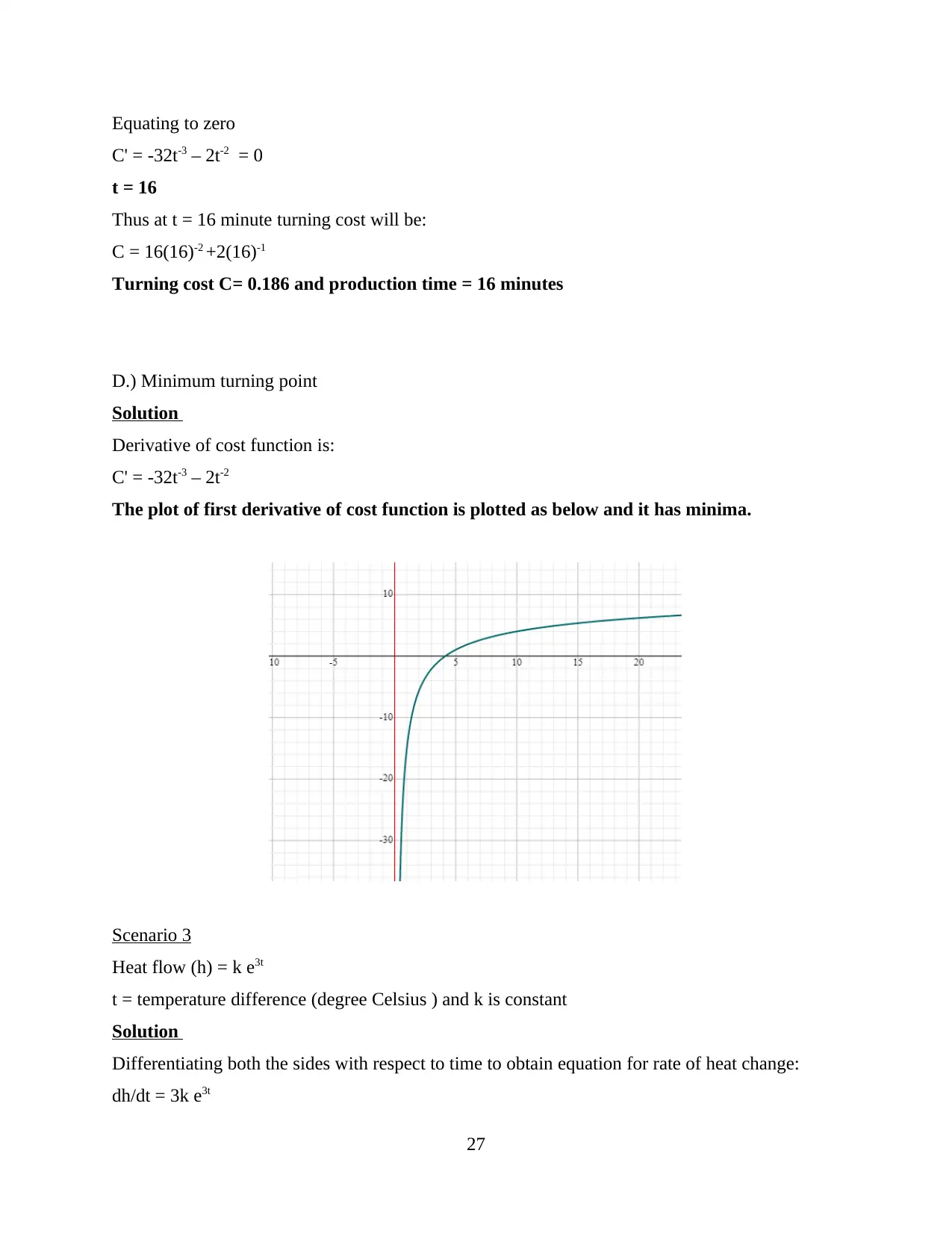
D.) Minimum turning point
Solution
Derivative of cost function is:
C' = -32t-3 – 2t-2
The plot of first derivative of cost function is plotted as below and it has minima.
Scenario 3
Heat flow (h) = k e3t
t = temperature difference (degree Celsius ) and k is constant
Solution
Differentiating both the sides with respect to time to obtain equation for rate of heat change:
dh/dt = 3k e3t
27

Thus the rate of change of heat = 3k e3t
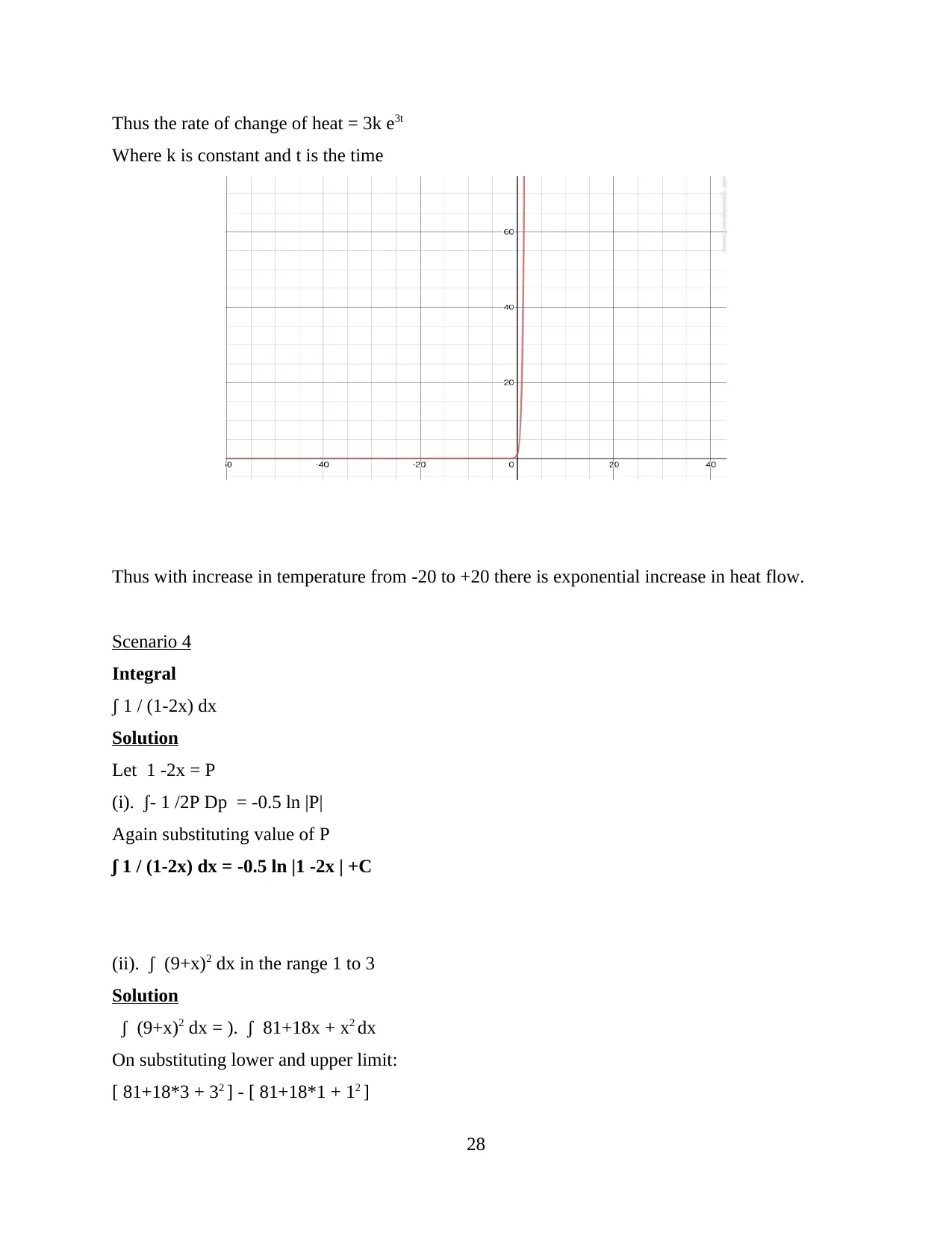
Where k is constant and t is the time
Thus with increase in temperature from -20 to +20 there is exponential increase in heat flow.
Scenario 4
Integral
ʃ 1 / (1-2x) dx
Solution
Let 1 -2x = P
(i). ʃ- 1 /2P Dp = -0.5 ln |P|
Again substituting value of P
ʃ 1 / (1-2x) dx = -0.5 ln |1 -2x | +C
(ii). ʃ (9+x)2 dx in the range 1 to 3
Solution
ʃ (9+x)2 dx = ). ʃ 81+18x + x2 dx
On substituting lower and upper limit:
[ 81+18*3 + 32 ] - [ 81+18*1 + 12 ]
28

= 242.66
ʃ (9+x)2 dx in the range 1 to 3 = 242.66
29