Business Analytics: Linear Programming, Decision Trees and Payoff Tables

This content covers Linear Programming, Decision Trees and Payoff Tables in Business Analytics. It includes a detailed explanation of the formulation of Linear Programme for a decision problem, assumptions and limitations of Linear Programming, and limitations of the Decision Tree approach. It also provides a payoff table for Maximax, Minimin and Minimax strategies. The subject is Business Analytics and the course code is not mentioned. The content is relevant for students pursuing Business Analytics in any college or university.

Online Exam business analytics

TABLE OF CONTENTS
QUESTION 3...................................................................................................................................3
a...................................................................................................................................................3
b...................................................................................................................................................4
c...................................................................................................................................................4
d...................................................................................................................................................5
e...................................................................................................................................................5
QUESTION 4...................................................................................................................................6
a...................................................................................................................................................6
b...................................................................................................................................................8
QUESTION 5...................................................................................................................................8
1...................................................................................................................................................8
2...................................................................................................................................................8
REFERENCES..............................................................................................................................10

QUESTION 3
a.
Formulation of Linear programme for a decision problem
Modelling the objective function
Objective is to have the smallest possible capital investment = Minimization
Let the number of 1 tonne van be x1 and the number of 2 tonne van be x2.
Cost of x1 or 1 tonne van = £25,000
Cost of x2 or 2 tonne van = £50,000
Minimization = x1* £25,000 + x2 * £50,000 – Objective function
Modelling the constraints
1x1 + 3x2 < or = 35 (For additional staff)
x1 > or = 6 (Minimum number 1 tonne van must be bought)
1x1 + 2x2 > or = 60 (for the minimum increase in the total truck capacity)
x1, x2 > or = 0 (non – negativity)
x1 x2
z 25000 50000
c1 1 3 <= 35
c2 1 0 >= 6
c3 1 2 >= 60
c1
x1 x2
35 0
0 11.7
c2
x1 x2
6 0
0 0
c3
x1 x2

60 0
0 30
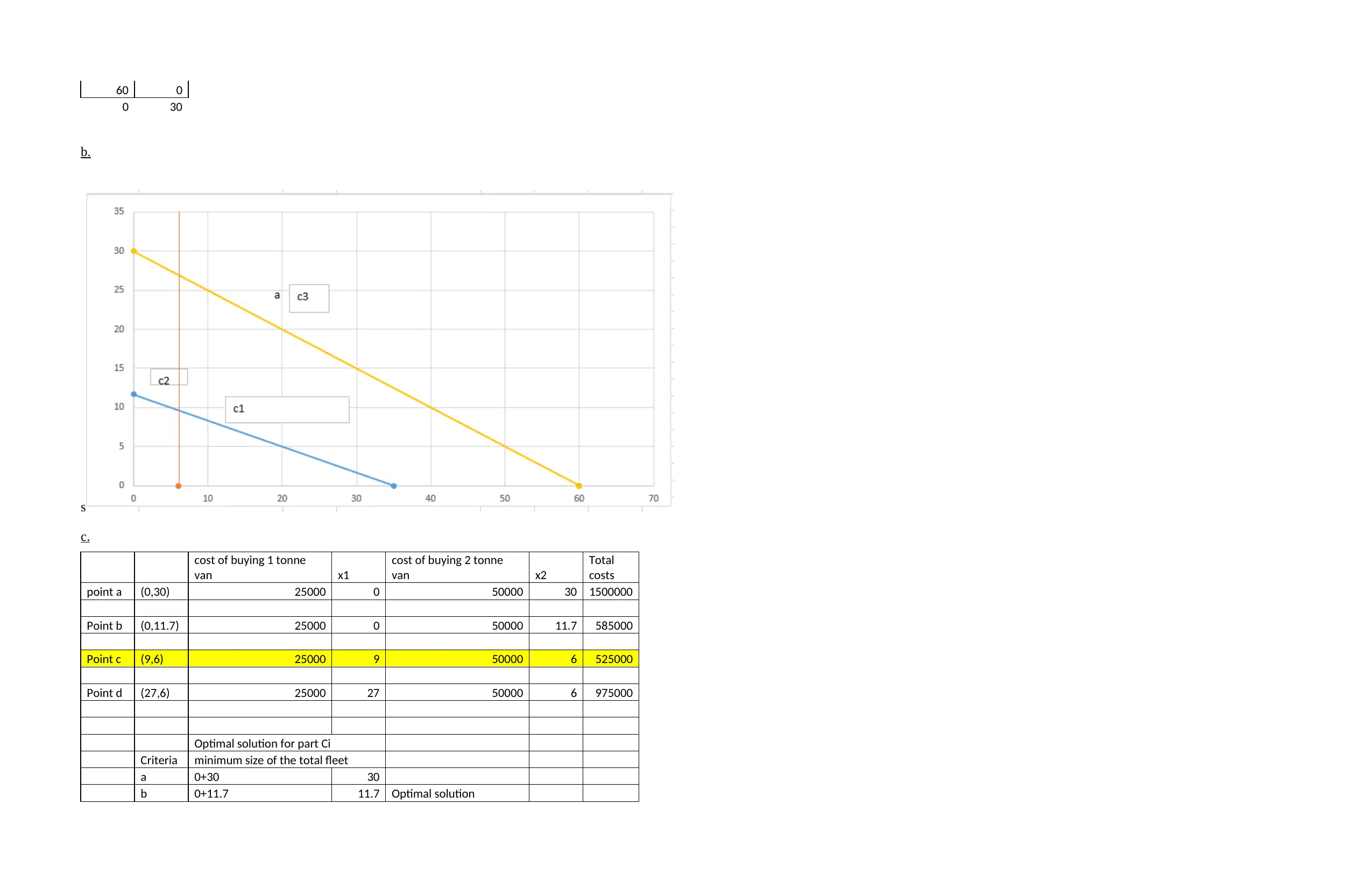
b.
s
c.
cost of buying 1 tonne
van x1
cost of buying 2 tonne
van x2
Total
costs
point a (0,30) 25000 0 50000 30 1500000
Point b (0,11.7) 25000 0 50000 11.7 585000
Point c (9,6) 25000 9 50000 6 525000
Point d (27,6) 25000 27 50000 6 975000
Optimal solution for part Ci
Criteria minimum size of the total fleet
a 0+30 30
b 0+11.7 11.7 Optimal solution

c 9+6 15
d 27+6 33
Optimal solution to cii
Criteria required minimum additional staff
a 30*3 90
b 11.7*3 35.1
c 9*1+6*3 27 Optimal solution cii
d 27*1+6*3 45
d.
Optimal solution
(50000- 2000) * 6+ (25000 – x) * 9 = 525000
525000 = 288000 + 225000 – 9x
X = 12000 / 9= 1333
With the above calculation it is clear that the discount for purchase price is 1333.
e.
Linear programming assumptions and limitations
Linear programming is being defined as the method through which the objective function it either maximize or minimize within the given mathematical model.
The assumption of linear programming are as follows-
 Proportionality- this assumption states that the rate of change that is slope of the objective function and relating to constraint equation is assumed to be constant.
 Additivity- this is another assumption which states that terms being present in the constraint and objective function is always additive (He, 2020).
 Certainty- this assumption of linear programming states that values relating to all model parameters are assumed for having known with certainty that is non- probabilistic.
Along with these assumptions there are some limitation of linear programming which are as follows-
 The main limitation of linear programming is that it is difficult to formulate the objectives function
 Another limitation of LP is that the constraint within linear form is difficult to express.
QUESTION 4
a.

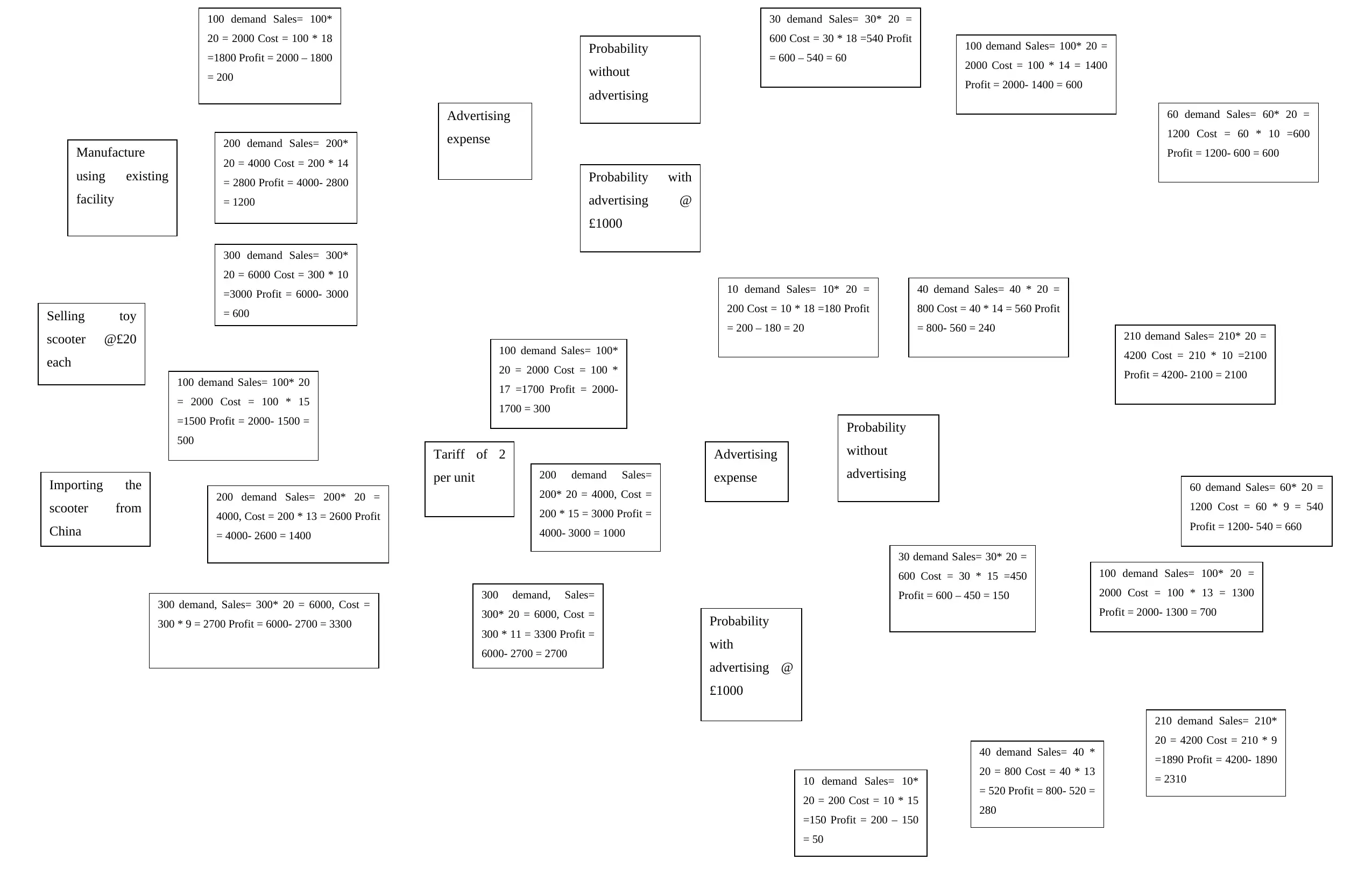
Selling toy
scooter @£20
each
Manufacture
using existing
facility
Importing the
scooter from
China
100 demand Sales= 100*
20 = 2000 Cost = 100 * 18
=1800 Profit = 2000 – 1800
= 200
300 demand Sales= 300*
20 = 6000 Cost = 300 * 10
=3000 Profit = 6000- 3000
= 600
200 demand Sales= 200*
20 = 4000 Cost = 200 * 14
= 2800 Profit = 4000- 2800
= 1200
100 demand Sales= 100* 20
= 2000 Cost = 100 * 15
=1500 Profit = 2000- 1500 =
500
200 demand Sales= 200* 20 =
4000, Cost = 200 * 13 = 2600 Profit
= 4000- 2600 = 1400
300 demand, Sales= 300* 20 = 6000, Cost =
300 * 9 = 2700 Profit = 6000- 2700 = 3300
Tariff of 2
per unit
100 demand Sales= 100*
20 = 2000 Cost = 100 *
17 =1700 Profit = 2000-
1700 = 300
200 demand Sales=
200* 20 = 4000, Cost =
200 * 15 = 3000 Profit =
4000- 3000 = 1000
300 demand, Sales=
300* 20 = 6000, Cost =
300 * 11 = 3300 Profit =
6000- 2700 = 2700
Advertising
expense
Probability
without
advertising
Probability with
advertising @
£1000
30 demand Sales= 30* 20 =
600 Cost = 30 * 18 =540 Profit
= 600 – 540 = 60
60 demand Sales= 60* 20 =
1200 Cost = 60 * 10 =600
Profit = 1200- 600 = 600
100 demand Sales= 100* 20 =
2000 Cost = 100 * 14 = 1400
Profit = 2000- 1400 = 600
210 demand Sales= 210* 20 =
4200 Cost = 210 * 10 =2100
Profit = 4200- 2100 = 2100
40 demand Sales= 40 * 20 =
800 Cost = 40 * 14 = 560 Profit
= 800- 560 = 240
10 demand Sales= 10* 20 =
200 Cost = 10 * 18 =180 Profit
= 200 – 180 = 20
Probability
without
advertising
Probability
with
advertising @
£1000
10 demand Sales= 10*
20 = 200 Cost = 10 * 15
=150 Profit = 200 – 150
= 50
30 demand Sales= 30* 20 =
600 Cost = 30 * 15 =450
Profit = 600 – 450 = 150
40 demand Sales= 40 *
20 = 800 Cost = 40 * 13
= 520 Profit = 800- 520 =
280
100 demand Sales= 100* 20 =
2000 Cost = 100 * 13 = 1300
Profit = 2000- 1300 = 700
210 demand Sales= 210*
20 = 4200 Cost = 210 * 9
=1890 Profit = 4200- 1890
= 2310
60 demand Sales= 60* 20 =
1200 Cost = 60 * 9 = 540
Profit = 1200- 540 = 660
Advertising
expense

by evaluating the above decision tree approach for the company is that they must go for the option of importing the scooter from China as this will be providing more profit and will assist company in increasing their
profitability.
b.
Limitations of the Decision Tree
 The major drawback of using the decision tree is that this method is not good in case when the data is large as it takes a lot of time to create the tree.
 In addition to this, another drawback of using the decision tree approach is that there are high chances of classification error and this affects the completion of the decision tree in proper and effective manner ( Hussein,
2021).
 Moreover, another limitation of using the decision tree approach is that this approach is not suitable for the variables which are continuous.
QUESTION 5
1.
Payoff table for Maximax
Cost
minor
accident
major
accident
basic insurance 125 100 1250
premium
insurance 160 0 200
Maximax = max (1250, 200)
= 1250
According to this basic insurance need to be followed
2.
a. Minimin strategy
Min (min) = (100, 0)
= 0
b. Minimax strategy
Min (max) = Min (1250, 200)
= 200
On the basis of the above calculation it is evident that the minimin strategy must be used by the company as in this situation the cost of the company is low.

REFERENCES
Books and Journals
He, S., 2020. Linear programming based evacuation models for a controlled freeway. arXiv preprint arXiv:2005.14353.
Hussein, M.S.E.O., 2021. DECISION TREE APPROACH FOR PLANTS STOPPAGE DECISION PROCESS DUE TO POWER LIMITATION CASE STUDY: STEEL COMPANY. Yanbu Journal of Engineering and
Science, 10(1), pp.14-23.