Regression Analysis for Cost Reduction

This document explains the importance of regression analysis in reducing production costs. It includes data, formulas, and calculations for determining the relationship between weight and height parameters.

BUSINESS ANALYTICS

BUSINESS ANALYTICS
Q1
i. The visualizations in the report are of very good quality with distinct colors and
visible labels. The report provides explanations with high quality graphics, this makes
it more presentable and understandable. The report also presents extensive and
relevant information on innovation in the retail business sector.
ii. The key information from the report include:
1. Up to 87% of retailers are either improvers or innovation active.
2. Up to 48% of retailers invest in sales and marketing.
3. The return on investment (ROI) for innovation investment in retail is 1.97.
This informs a retailer on market trend with respect to investment on growth and use
of innovation. This is useful in cases when, for instance, a retailer is faced with a
decision on how to utilize new investment.
iii. The purpose of the report is to present findings on innovation in the retail business
sectors in Australia for the year 2018. The report compares the findings for the
multichannel retailers, brick and mortar retailers, and purely online retailers with
respect to innovation. The report also compares the 2018 findings with the findings
for 2017. Multichannel retailers are the most innovation active retailers with retail
innovation activity slightly decreasing from 2017 to 2018.
iv. In order to improve this report, more precise visualizations have to be used with
inclusion of more explanations. The report appears to have too many graphic
visualizations and too few explanations. Merging or reducing graphs and increasing
explanations will improve the report
2

BUSINESS ANALYTICS
Q2
i. Regression analysis is an important statistical tool for determining methods for
reduction in the cost of production. Regression can be applied to determine which
factors significantly affect the cost of production for an entity. These factors can then
be adjusted appropriately to ensure that the cost of production is reduced without
affecting quality of product and profit margins for the entity.
ii. Table 1 contains data on 10 individuals with regards to weight (measured in
kilograms) and height (measured in feet) parameters.
Table 1
Individual Weight (in
Kilograms)
Height
(in feet)
1 55 5.7
2 54 5.5
3 57 5.1
4 56 7
5 52 4.2
6 56 5.3
7 57 6.7
8 57 5.7
9 57 5.6
10 56 6.1
iii. The graph in Figure 1: Scatterplot for Weight Versus Height below shows the plot of
Weight against Height for the 10 individuals in Table 1. Some data points in the
graph below align in a linear manner, however other data points equally fall outside
the linear alignment. This implies that there may exist some form linear relationship
but not significant enough to be considered as the general relationship between the
Weight and Height parameters.
3

BUSINESS ANALYTICS
4 4.5 5 5.5 6 6.5 7 7.5
49
50
51
52
53
54
55
56
57
58
Scatterplot for Weight Versus Height
Height
Weight
Figure 1: Scatterplot for Weight Versus Height
iv. The formulas below are used for computing the regression equation line.
β1=∑ (xi−xmean )( yi− ymean )
∑ ( xi−xmean)2
β0= ymean −β1 xmean
The calculations for the formulas above are given in Table 2 and Table 3 below:
Table 2
Weight = y Height = x
Sum 557 56.9
Mean 55.7 5.69
Table 3
xi−xmean (xi−xmean)2 yi− ymean ( xi−xmean)( yi− ymean)
0.01 1E-04 -0.7 -0.007
-0.19 0.0361 -1.7 0.323
-0.59 0.3481 1.3 -0.767
4

BUSINESS ANALYTICS
1.31 1.7161 0.3 0.393
-1.49 2.2201 -3.7 5.513
-0.39 0.1521 0.3 -0.117
1.01 1.0201 1.3 1.313
0.01 1E-04 1.3 0.013
-0.09 0.0081 1.3 -0.117
0.41 0.1681 0.3 0.123
∑ ¿-4.4E-15 ∑ ¿5.669 ∑ ¿-2.8E-
14
∑ ¿6.67
Thus the values for β1 and β0 are given as follows:
β1=∑ ( xi−xmean ) ( yi− ymean )
∑( xi−xmean )2 = 6.67
5.669 =1.177
β0= ymean −β1 xmean=55.7−1.177 ( 5.69 ) =49.34
The regression equation for a simple linear regression is given as [1]:
y=β0 + β1 x
Thus, the resultant regression equation for this case will be:
y=49.34+1.177 x
Weight=49.34+1.177 Height
v. The formula below is used for computing the R2.
R2= [ ∑ ( xi−xmean ) ( yi− ymean )
√ ∑ ( xi−xmean ) 2
∑ ( yi− y ) 2 ]
2
The calculations for the formula above is given in Table 4 below:
Table 4
( xi−xmean)2 ( yi− ymean)2 ( xi−xmean)( yi− ymean)
1E-04 0.49 -0.007
0.0361 2.89 0.323
0.3481 1.69 -0.767
5

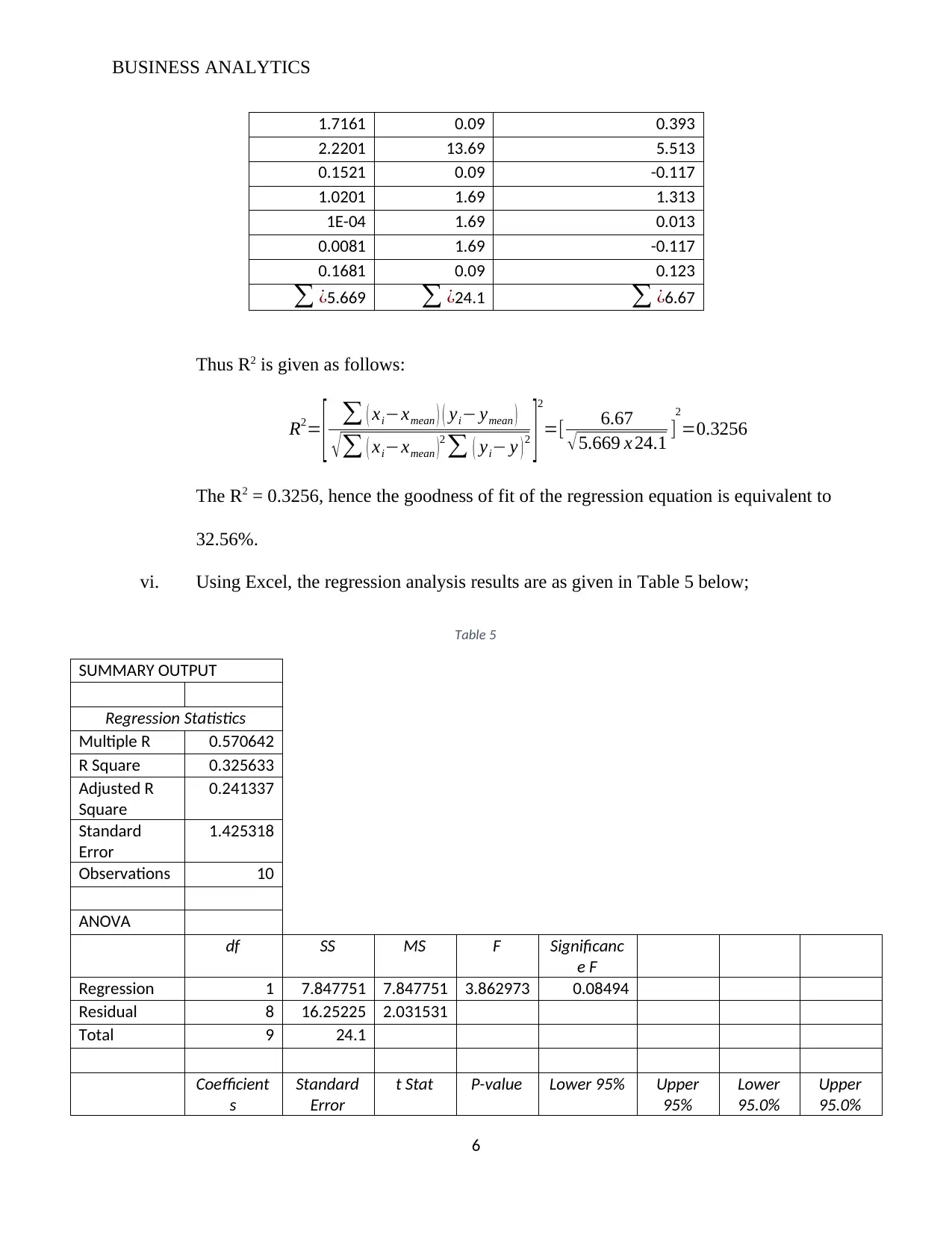
BUSINESS ANALYTICS
1.7161 0.09 0.393
2.2201 13.69 5.513
0.1521 0.09 -0.117
1.0201 1.69 1.313
1E-04 1.69 0.013
0.0081 1.69 -0.117
0.1681 0.09 0.123
∑ ¿5.669 ∑ ¿24.1 ∑ ¿6.67
Thus R2 is given as follows:
R2= [ ∑ ( xi−xmean ) ( yi− ymean )
√∑ ( xi−xmean )2
∑ ( yi− y ) 2 ]2
=[ 6.67
√5.669 x 24.1 ]
2
=0.3256
The R2 = 0.3256, hence the goodness of fit of the regression equation is equivalent to
32.56%.
vi. Using Excel, the regression analysis results are as given in Table 5 below;
Table 5
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.570642
R Square 0.325633
Adjusted R
Square
0.241337
Standard
Error
1.425318
Observations 10
ANOVA
df SS MS F Significanc
e F
Regression 1 7.847751 7.847751 3.862973 0.08494
Residual 8 16.25225 2.031531
Total 9 24.1
Coefficient
s
Standard
Error
t Stat P-value Lower 95% Upper
95%
Lower
95.0%
Upper
95.0%
6

BUSINESS ANALYTICS
Intercept 49.00529 3.435897 14.26274 5.69E-07 41.0821 56.92848 41.0821 56.92848
X Variable 1 1.176574 0.59863 1.965445 0.08494 -0.20387 2.557018 -0.20387 2.557018
From Table 5 above, the resultant regression equation is given as:
y=49.00529+1.176574 x
Weight=49.00529+1.176574 Height
Also from Table 5 above, the R2 = 0.325633
Comparing these results to those obtained in parts iv and v above, we observe that the
values are consistent with each other.
Q3
i. Classification can be defined as the categorization of items or subjects into
homogenous groups in terms of characteristics while prediction is the forecasting of
future values of a parameter of interest [2].
ii. Classification methods include:
1. K-means clustering
2. Hierarchical clustering
3. Neural Nets
iii. The algebraic equation for the neural network is as given below:
yi= w 5
1+e− ( b 1 +i1 w 1+ i2 w 3 ) + w 6
1+ e− ( b 2+i 1 w 2+i 2 w 4 )
In classification, the groups of the output variable are usually assigned factors; 0, 1,
…, depending on the number of groups (categories). The output value of the neural
7

BUSINESS ANALYTICS
network is compared to cutoff values that specify where the subject is classified if the
output value exceeds or is below the cutoff value.
iv. The applications of clustering in business analytics include the following scenarios:
1. Suppose a retailer is interested in identifying the sales similarity for goods at their
retail stores. The retailer can use clustering to group the goods according to
homogeneity in sales.
2. Consider a case in which a company is interested in developing customized
marketing approach for its customers. The company can use clustering to group
its customers depending on certain criteria and then develop the customized
marketing approach for each of the groups.
3. Suppose a bank is interested in the analysis of the credit worthiness of loan
applicants. The bank can use clustering to group the loan applicants depending on
the various parameters of interest so as to map the loan applicants.
8

BUSINESS ANALYTICS
REFERENCES
[1] D. A. Freedman, Statistical Models: Theory and Practice, London: Cambridge University
Press, 2009.
[2] S. Galit, B. C. Peter, Y. Inbal, N. R. Patel and L. C. Kenneth, Data Mining for Business
Analytics, 1st ed., New Delhi: John Wiley & Sons, Inc., 2018.
9