Business Data Analysis: Preparation Time and Exam Marks

This article discusses the relationship between preparation time and exam marks using cross-sectional survey and simple random sampling. It analyzes the data using histograms, scatter plots, regression models, and correlation analysis. A descriptive summary of the two variables is also provided.

AFE135 SP 3
Business Data Analysis
1

ANS: Cross-sectional survey method could be used for collecting the
requisite fields of information. This particular survey method is generally
used to collect data for a specific issue at a particular point of time. Hence,
collecting information about preparation hours and examination marks from
100 students would be preferable by cross-sectional survey method.
ANS: Simple random sampling could be used by the researcher to collect
information from the target population of students. Choice of population
would be on the basis of convenience, but selection of sample data would
be in a random manner from the population.
ANS: Based on the research question, the dependent variable should be the
marks obtained in the examination. The preparation time spent (in hours)
should be considered as the independent variable to see the impact on
marks obtained. Marks obtained in the exam is an interval type variable
(discrete), and hours of study is ratio level data type (continuous).
ANS: Issues such as timing of the interview, total time to collect the sample
data could be the two primary problems. Probable biasness in the sample
due to the fact that exact cause and effect could not be assessed at the
time of sampling could be an important issue. Associated cost could be
another matter of concern (Nardi, 2018).
2

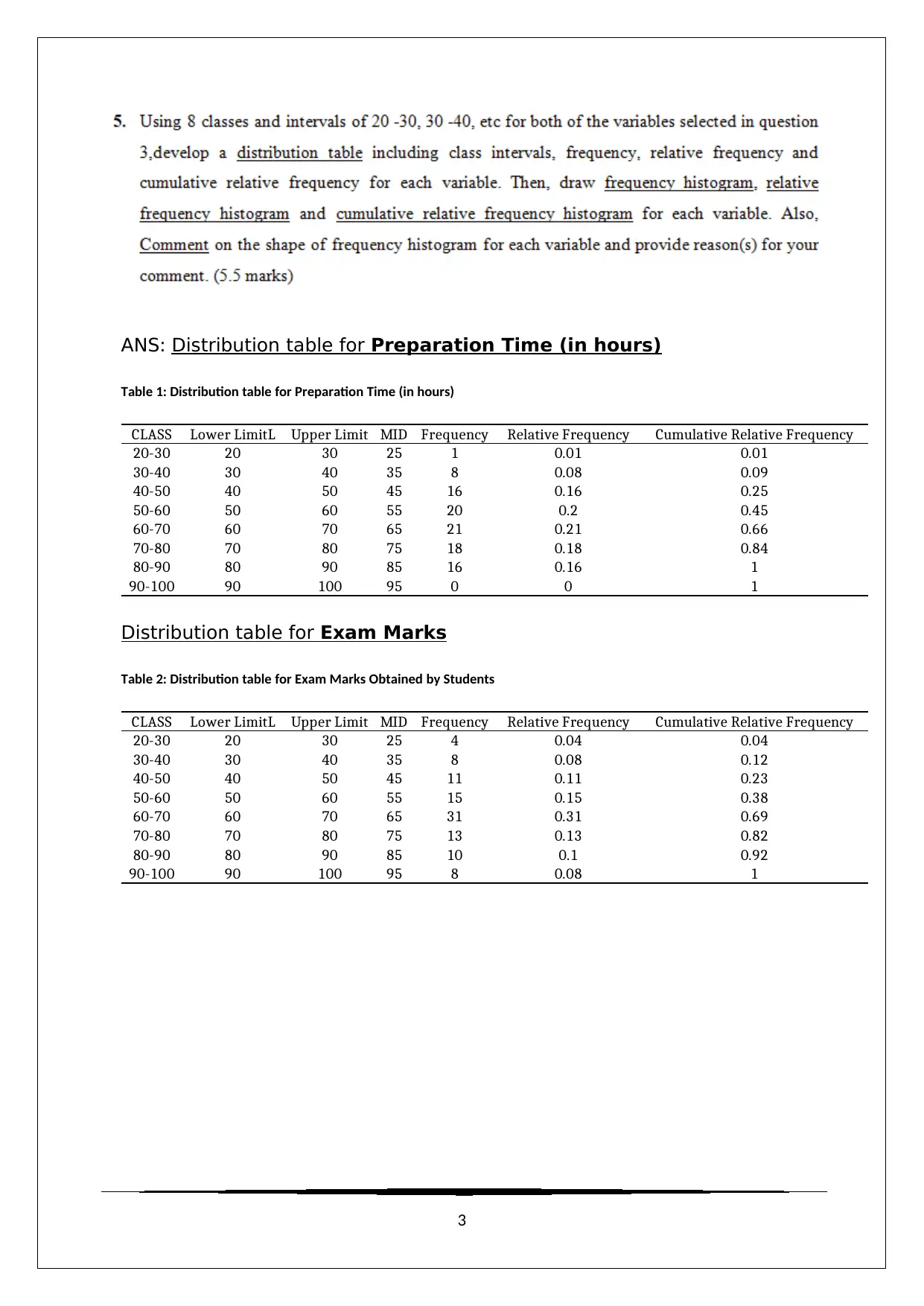
ANS: Distribution table for Preparation Time (in hours)
Table 1: Distribution table for Preparation Time (in hours)
CLASS Lower LimitL Upper Limit MID Frequency Relative Frequency Cumulative Relative Frequency
20-30 20 30 25 1 0.01 0.01
30-40 30 40 35 8 0.08 0.09
40-50 40 50 45 16 0.16 0.25
50-60 50 60 55 20 0.2 0.45
60-70 60 70 65 21 0.21 0.66
70-80 70 80 75 18 0.18 0.84
80-90 80 90 85 16 0.16 1
90-100 90 100 95 0 0 1
Distribution table for Exam Marks
Table 2: Distribution table for Exam Marks Obtained by Students
CLASS Lower LimitL Upper Limit MID Frequency Relative Frequency Cumulative Relative Frequency
20-30 20 30 25 4 0.04 0.04
30-40 30 40 35 8 0.08 0.12
40-50 40 50 45 11 0.11 0.23
50-60 50 60 55 15 0.15 0.38
60-70 60 70 65 31 0.31 0.69
70-80 70 80 75 13 0.13 0.82
80-90 80 90 85 10 0.1 0.92
90-100 90 100 95 8 0.08 1
3

Figure 1: Histogram for Frequency Distribution of Preparation Time
Shape of the frequency histogram was almost normal with small amount of negative skewness.
Insignificant frequency in the first class of 20 – 30, and presence of high frequency in the right tail
was the primary reason for this probable negative skewness (Spiegel, & Stephens, 2017).
Figure 2: Histogram for Relative Frequency Distribution of Preparation Time
4

Figure 3: Histogram for Cumulative Relative Frequency Distribution of Preparation Time
Shape of the frequency histogram was almost normally distributed. A small amount of negative
skewness was identified due to the fact that the median was slightly deviated from the middle
position of the histogram x-axis. The presence of median in the class 60 – 70 was the primary
reason for this probable negative skewness.
Figure 4: Histogram for Frequency Distribution of Exam Marks
5

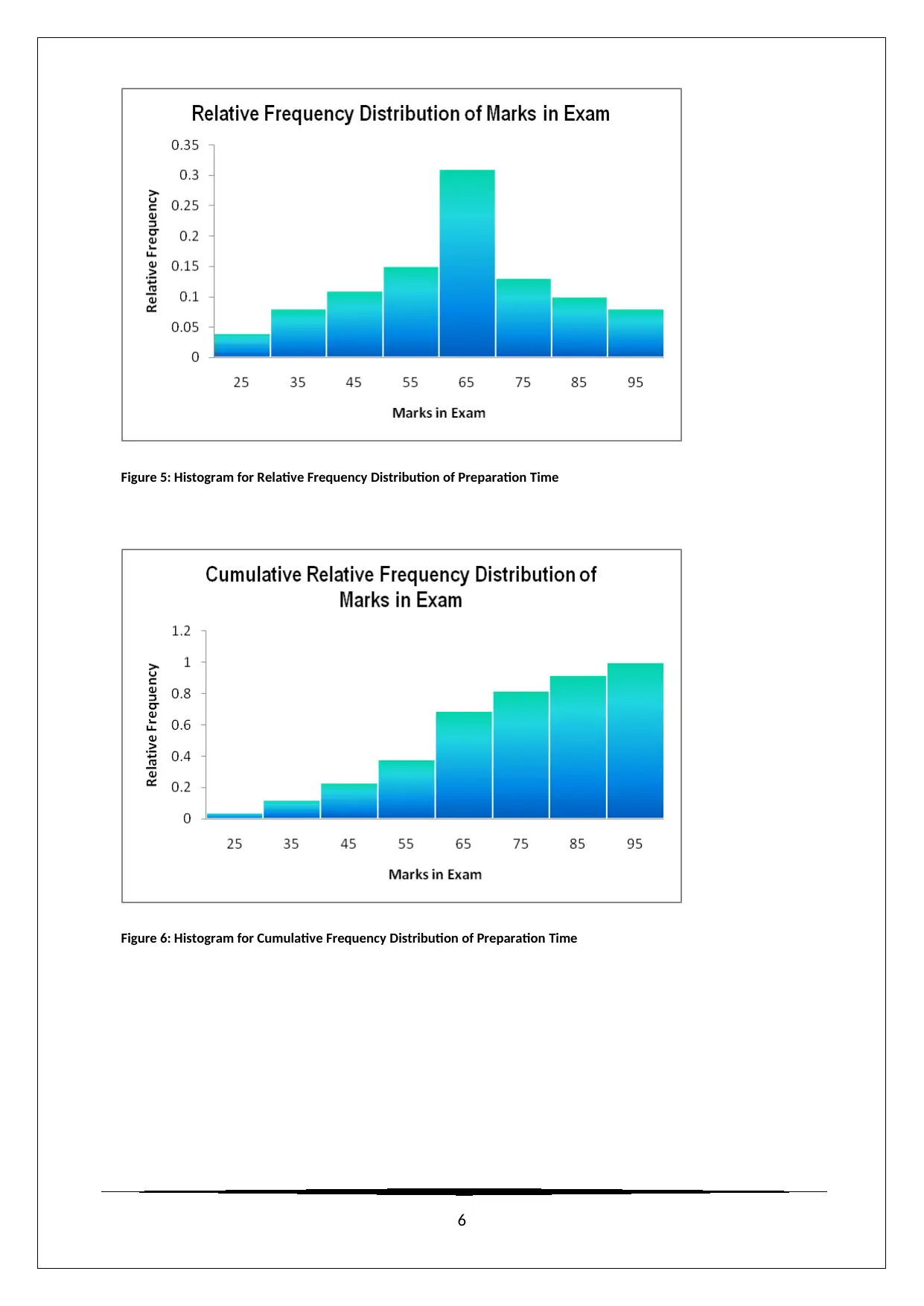
Figure 5: Histogram for Relative Frequency Distribution of Preparation Time
Figure 6: Histogram for Cumulative Frequency Distribution of Preparation Time
6

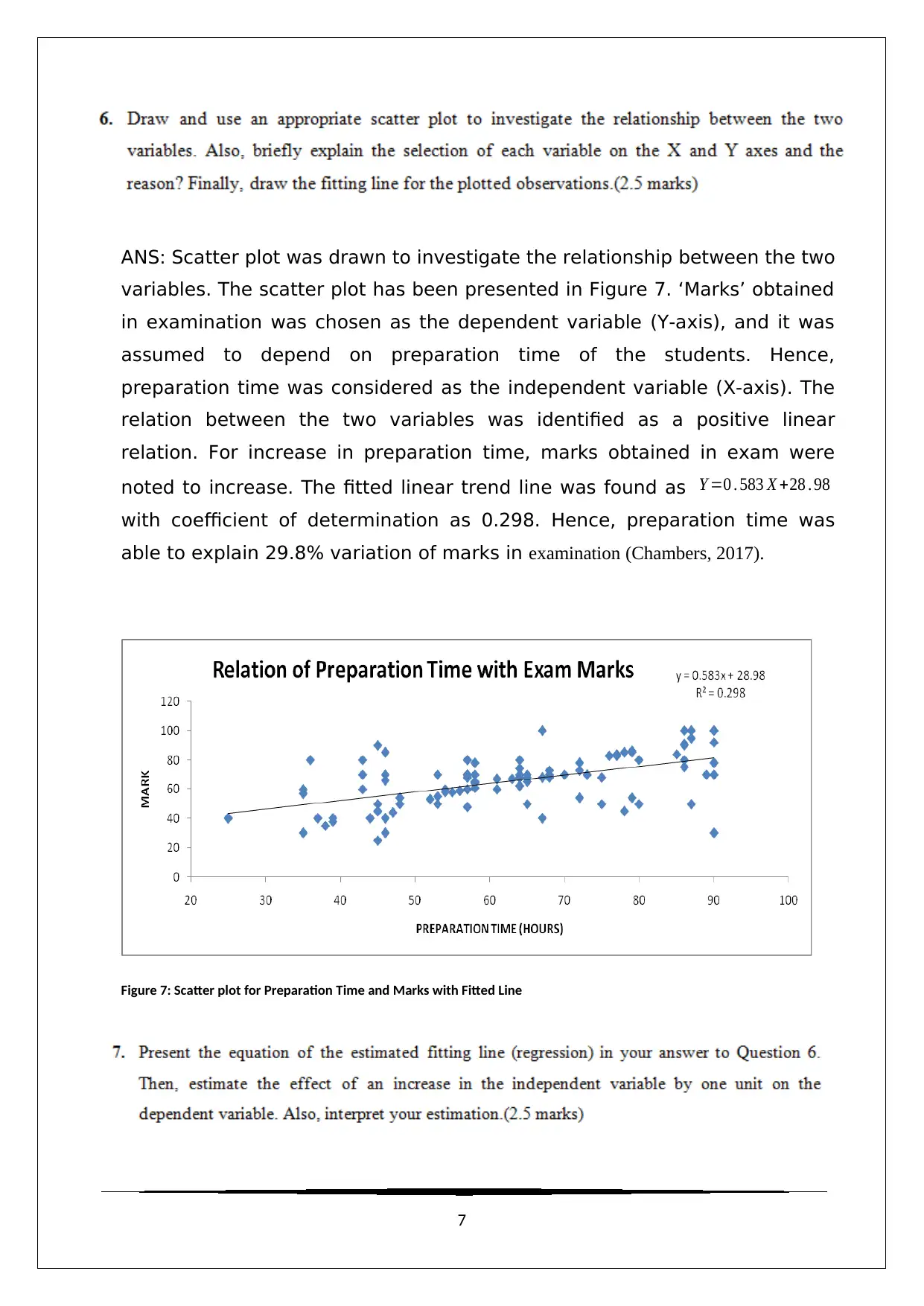
ANS: Scatter plot was drawn to investigate the relationship between the two
variables. The scatter plot has been presented in Figure 7. ‘Marks’ obtained
in examination was chosen as the dependent variable (Y-axis), and it was
assumed to depend on preparation time of the students. Hence,
preparation time was considered as the independent variable (X-axis). The
relation between the two variables was identified as a positive linear
relation. For increase in preparation time, marks obtained in exam were
noted to increase. The fitted linear trend line was found as Y =0 . 583 X +28 . 98
with coefficient of determination as 0.298. Hence, preparation time was
able to explain 29.8% variation of marks in examination (Chambers, 2017).
Figure 7: Scatter plot for Preparation Time and Marks with Fitted Line
7

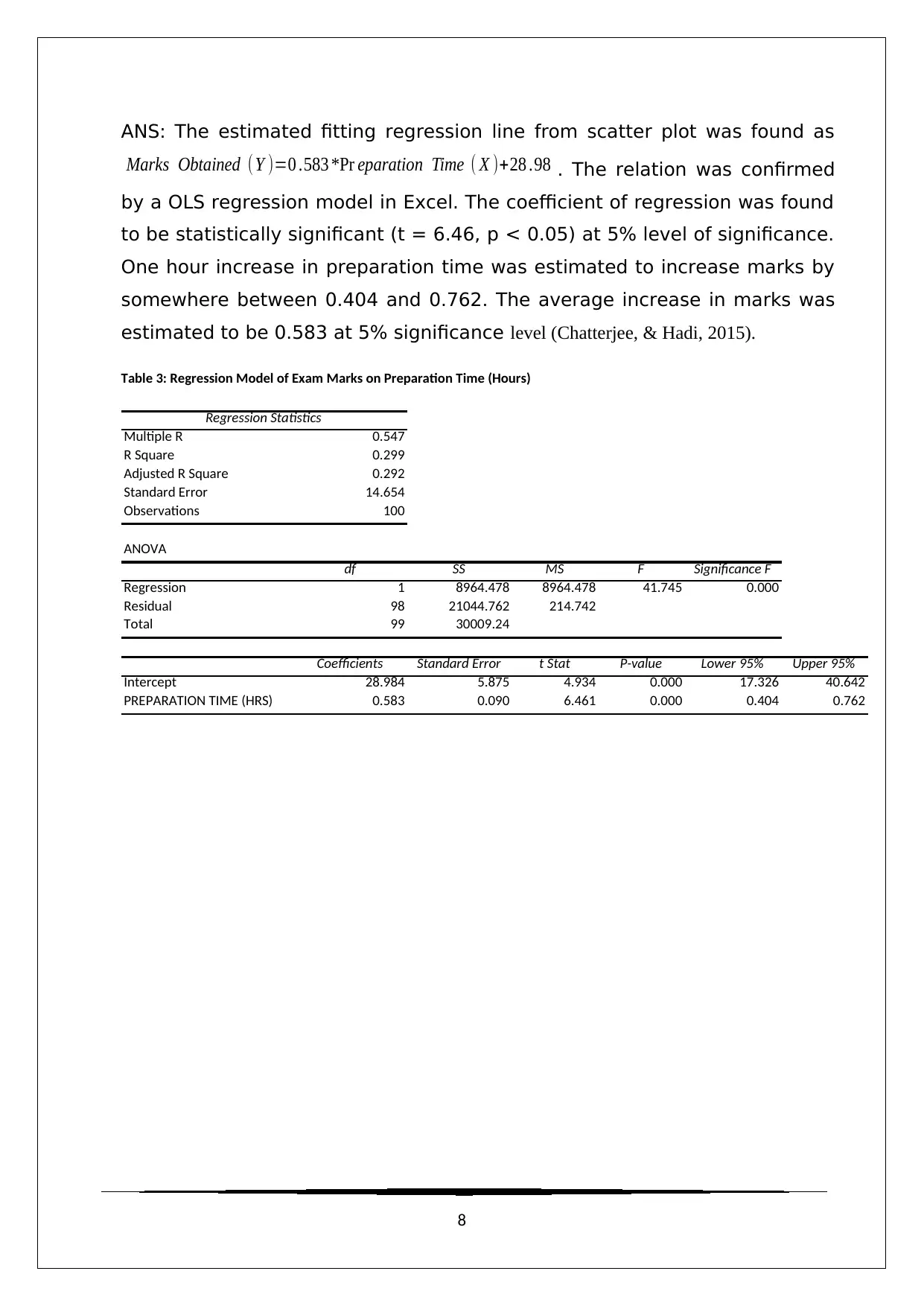
ANS: The estimated fitting regression line from scatter plot was found as
Marks Obtained (Y )=0 .583 *Pr eparation Time ( X )+28 .98 . The relation was confirmed
by a OLS regression model in Excel. The coefficient of regression was found
to be statistically significant (t = 6.46, p < 0.05) at 5% level of significance.
One hour increase in preparation time was estimated to increase marks by
somewhere between 0.404 and 0.762. The average increase in marks was
estimated to be 0.583 at 5% significance level (Chatterjee, & Hadi, 2015).
Table 3: Regression Model of Exam Marks on Preparation Time (Hours)
Regression Statistics
Multiple R 0.547
R Square 0.299
Adjusted R Square 0.292
Standard Error 14.654
Observations 100
ANOVA
df SS MS F Significance F
Regression 1 8964.478 8964.478 41.745 0.000
Residual 98 21044.762 214.742
Total 99 30009.24
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 28.984 5.875 4.934 0.000 17.326 40.642
PREPARATION TIME (HRS) 0.583 0.090 6.461 0.000 0.404 0.762
8

ANS: Descriptive summary report about the data on the two variables was
constructed as below.
Table 4: Descriptive Summary of the Two Variables
Descriptives PREPARATION TIME (HRS) MARK
Mean 63.04 65.74
Median 64 68
Standard Deviation 16.321 17.410
Sample Variance 266.362 303.124
Range 65 75
Minimum 25 25
Maximum 90 100
Quartile- 1 51 54
Quartile- 2 64 68
Quartile- 3 76.25 78
Interquartile Range 25.25 24
30th Percentile 54 58
Average preparation time was calculated as 63.04 hours (SD = 16.32),
which was very close to the median of the distribution. Location of median
at the right of the mean value indicated that the distribution is slightly
negatively skewed or almost normal. 50% of the students were found to
study less than 64 hours, whereas lowest 30% were found to study 54 hours
in average. The maximum study hour was noted as 90 hours and the
minimum study by any student was found to be 25 hours. The middle 50%
students were identified with a spread of approximately 25 hours of study.
An average mark in exam was calculated as 65.74 (SD = 17.41), which
was close to the median of the distribution. Location of median at the right
of the mean value indicated that the distribution is slightly negatively
skewed or almost normal. 50% of the students were found to obtain marks
less than 68, whereas lowest 30% were found to obtain 58. The maximum
9

exam score was noted as 100, and the minimum mark obtained by any
student was found to be 25. The middle 50% students were identified to
obtain a spread of approximately 24 marks.
ANS: A numerical measurement measuring the strength and direction of the
linear relationship between the two variables was evaluated by Pearson’s
correlation. The correlation (r = 0.547, p < 0.05) was statistically
significant, and it indicated that marks obtained in the exam had a high
positive and significant correlation with preparation time before exams. The
correlation value implied that for increase in preparation time, the obtained
marks would also strongly increase. The assumption of class instructors was found to
be statistically significant and true (Darlington, & Hayes, 2016).
Table 5: Correlation Matrix for Preparation Time and Marks Obtained
Correlation PREPARATION TIME (HRS) MARK
PREPARATION TIME (HRS) 1
MARK 0.547 1
10

References
Darlington, R. B., & Hayes, A. F. (2016). Regression analysis and linear models: Concepts,
applications, and implementation. Guilford Publications.
Chatterjee, S., & Hadi, A. S. (2015). Regression analysis by example. John Wiley & Sons.
Chambers, J. M. (2017). Graphical Methods for Data Analysis: 0. Chapman and Hall/CRC.
Nardi, P. M. (2018). Doing survey research: A guide to quantitative methods. Routledge.
Spiegel, M. R., & Stephens, L. J. (2017). Schaum's outline of statistics. McGraw Hill Professional.
11