Business Data Analysis - Trimester 2, 2018 - Computer Assignment

Business Data Analysis
Trimester 2, 2018
Computer Assignment

PART 1
1. The researcher collected data on two fields, preparation time for examination of the students
and their marks in examination. The sample size was large enough for statistical purpose,
but not that big for longitudinal survey. Hence, the researcher could have used questionnaire
method with cross sectional survey. This survey would have helped the researcher to find
therelation between the two variables, as described in a comapritive study.
2. As the questions were probably asked to students from same class or course, the researcher
could have used convienience sampling method from a specified population. The skewed
distribution pattern of preparation hours and almost normal pattern of marks also justified
the probable choice of the sampling technique (Etikan, Musa, & Alkassim, 2016).
3. Marks of the students and their preparation time were ratio level variables. For a proper
comparitive study the researcher should collect information about gender, age, class, and
subject combinations of the students.
4. Time for collecting the information and could have been the main problem, considering the
fact that collecting information from the population of the students always takes time. Also,
lost information due to convienience sampling was a major issue in the sampling process.

PART 2
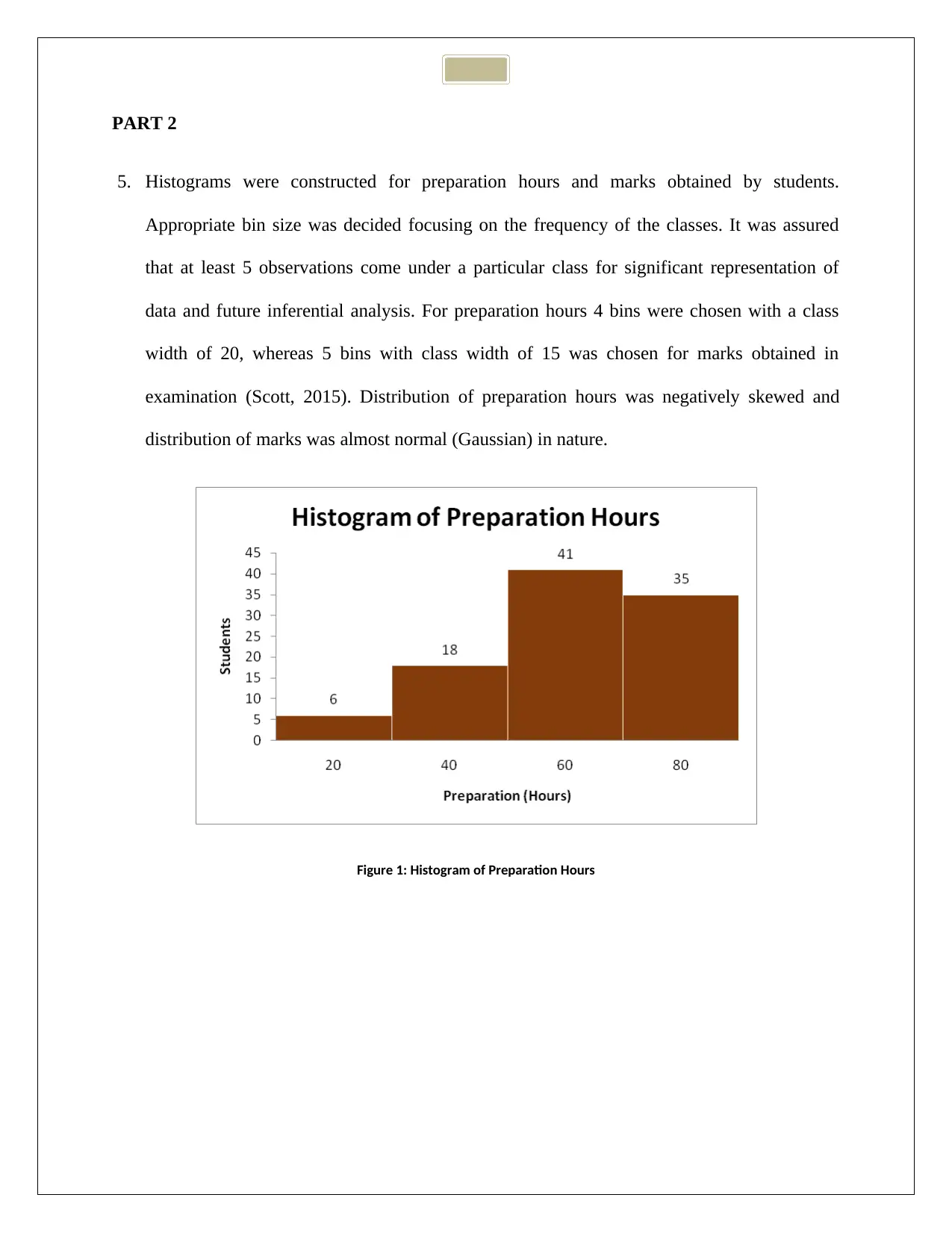
5. Histograms were constructed for preparation hours and marks obtained by students.
Appropriate bin size was decided focusing on the frequency of the classes. It was assured
that at least 5 observations come under a particular class for significant representation of
data and future inferential analysis. For preparation hours 4 bins were chosen with a class
width of 20, whereas 5 bins with class width of 15 was chosen for marks obtained in
examination (Scott, 2015). Distribution of preparation hours was negatively skewed and
distribution of marks was almost normal (Gaussian) in nature.
Figure 1: Histogram of Preparation Hours