Confidence Interval for Eggs and Cows

This document provides an analysis of confidence intervals for eggs and cows. It explains the concept of confidence interval and its factors. The analysis includes the calculation of confidence intervals for different chicken breeds' eggs and different types of cows' milk. Based on the results, recommendations are given for the company's operations.

Business Data Analysis

Table of Contents
Confidence interval....................................................................................................................3
Solution 1...............................................................................................................................3
Solution 2...............................................................................................................................5
Bibliography...............................................................................................................................5
Appendix....................................................................................................................................6
Calculations for Question 1....................................................................................................6
Calculations for Question 2....................................................................................................7

Confidence interval
The confidence interval can be described as an interval or range of values in which we can
surely state that the true value required by us lies. There are three major factors governing
confidence interval. They include - confidence level, margin of error and statistic (Altman et
al., 2013). The confidence level chosen for this problem is 99%. It means that the chances of
getting the population parameter within the calculated interval will be 99%. The confidence
interval will be calculated using the formula mentioned below:
Confidence Interval Formula:
Where:
x̄ = mean of the data
s = standard deviation
n = number of observations
z = chosen z-value for chosen confidence interval (for 99%, z-value is 2.576)
t = t-distribution with degrees of freedom (DF)
α = value of 100% - (Level of Confidence)
(Williamson et al., 2010)
Solution 1
For the calculation of the confidence interval, a random sample of 170 eggs from the daily
production was considered. The eggs were chosen from three chicken breeds including
Rhode Island Red, White Leghorn and Welsomer. The following table gives an account of
the weights of the chickens and its categorisation.

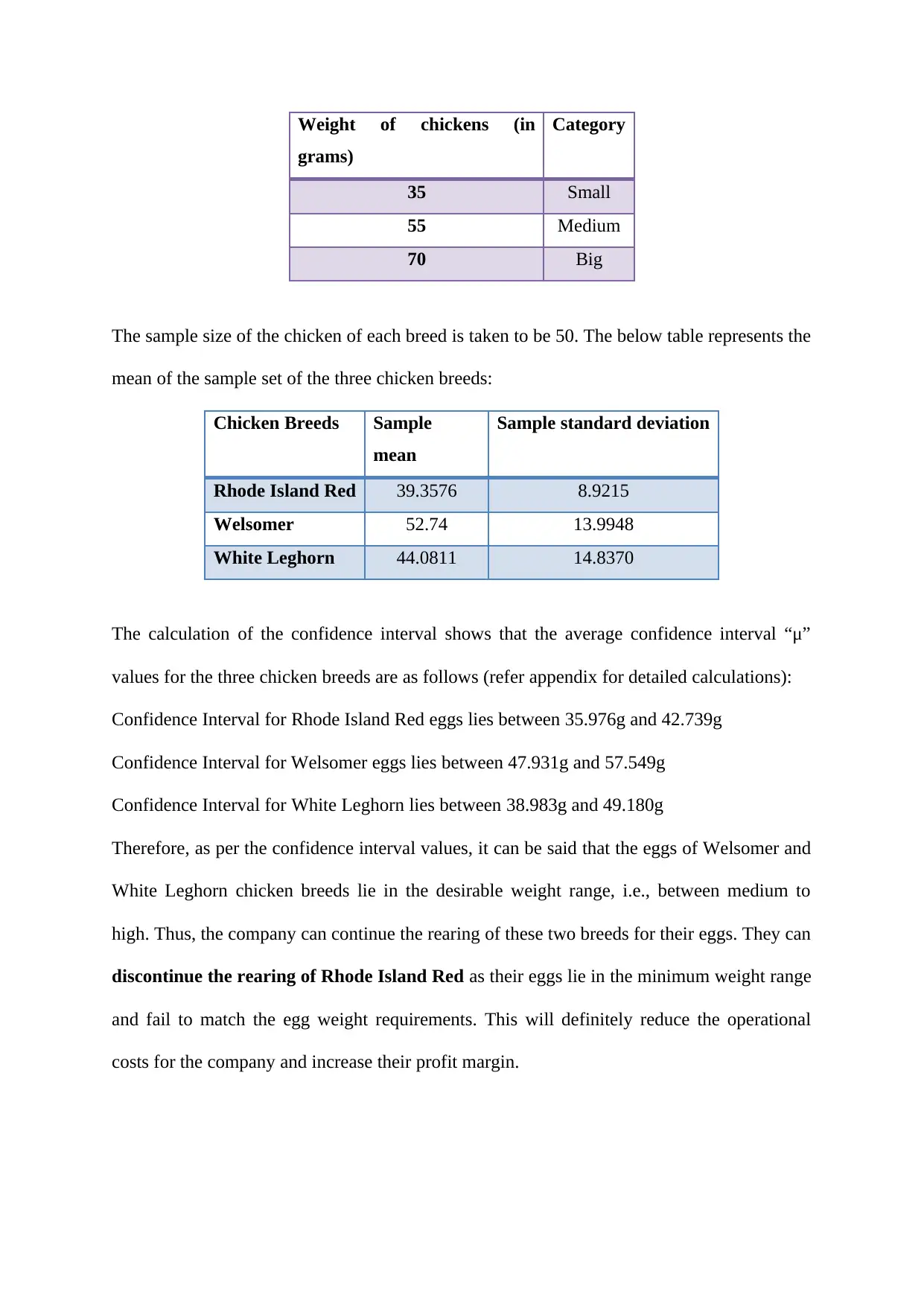
Weight of chickens (in
grams)
Category
35 Small
55 Medium
70 Big
The sample size of the chicken of each breed is taken to be 50. The below table represents the
mean of the sample set of the three chicken breeds:
Chicken Breeds Sample
mean
Sample standard deviation
Rhode Island Red 39.3576 8.9215
Welsomer 52.74 13.9948
White Leghorn 44.0811 14.8370
The calculation of the confidence interval shows that the average confidence interval “μ”
values for the three chicken breeds are as follows (refer appendix for detailed calculations):
Confidence Interval for Rhode Island Red eggs lies between 35.976g and 42.739g
Confidence Interval for Welsomer eggs lies between 47.931g and 57.549g
Confidence Interval for White Leghorn lies between 38.983g and 49.180g
Therefore, as per the confidence interval values, it can be said that the eggs of Welsomer and
White Leghorn chicken breeds lie in the desirable weight range, i.e., between medium to
high. Thus, the company can continue the rearing of these two breeds for their eggs. They can
discontinue the rearing of Rhode Island Red as their eggs lie in the minimum weight range
and fail to match the egg weight requirements. This will definitely reduce the operational
costs for the company and increase their profit margin.

Solution 2
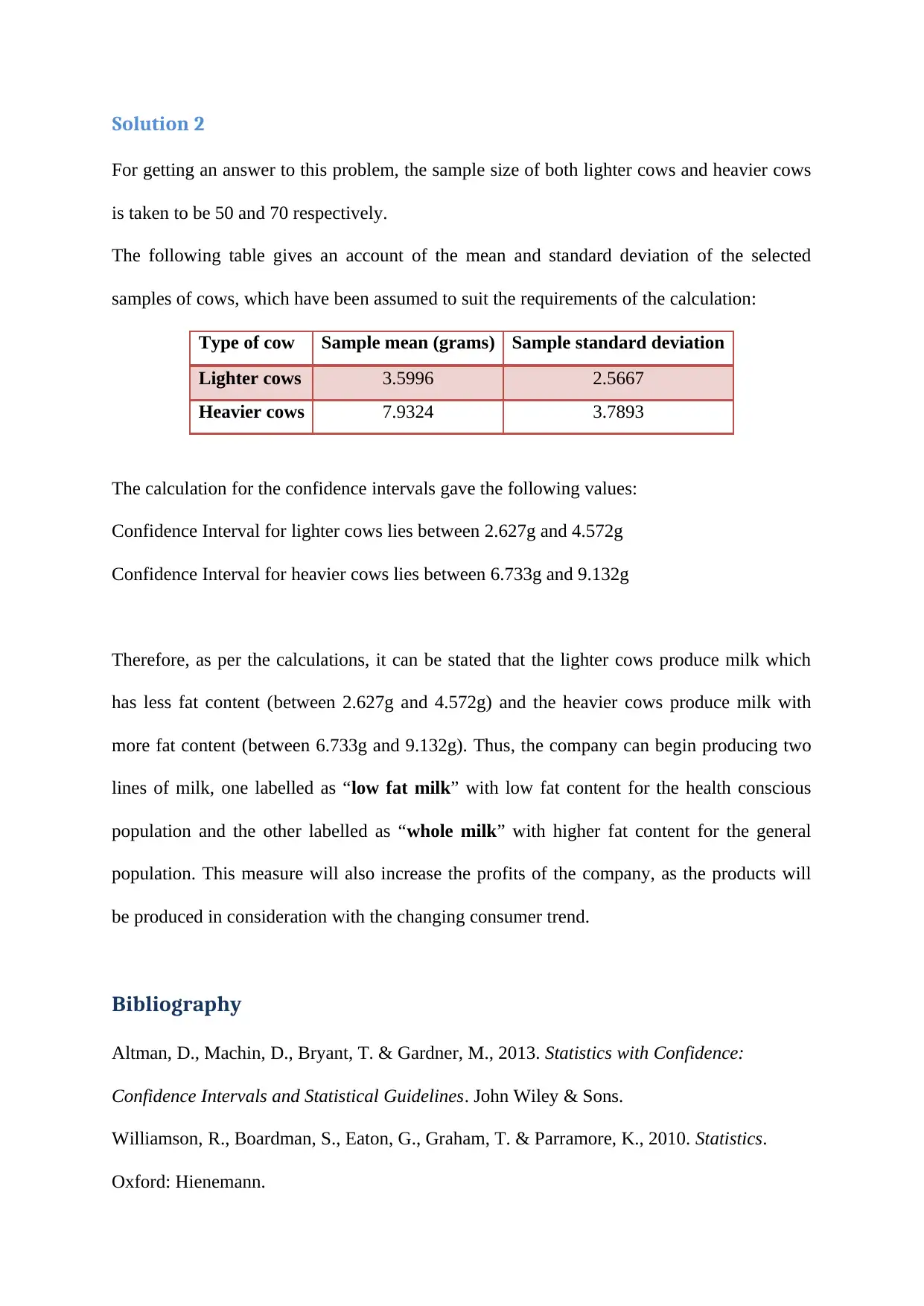
For getting an answer to this problem, the sample size of both lighter cows and heavier cows
is taken to be 50 and 70 respectively.
The following table gives an account of the mean and standard deviation of the selected
samples of cows, which have been assumed to suit the requirements of the calculation:
Type of cow Sample mean (grams) Sample standard deviation
Lighter cows 3.5996 2.5667
Heavier cows 7.9324 3.7893
The calculation for the confidence intervals gave the following values:
Confidence Interval for lighter cows lies between 2.627g and 4.572g
Confidence Interval for heavier cows lies between 6.733g and 9.132g
Therefore, as per the calculations, it can be stated that the lighter cows produce milk which
has less fat content (between 2.627g and 4.572g) and the heavier cows produce milk with
more fat content (between 6.733g and 9.132g). Thus, the company can begin producing two
lines of milk, one labelled as “low fat milk” with low fat content for the health conscious
population and the other labelled as “whole milk” with higher fat content for the general
population. This measure will also increase the profits of the company, as the products will
be produced in consideration with the changing consumer trend.
Bibliography
Altman, D., Machin, D., Bryant, T. & Gardner, M., 2013. Statistics with Confidence:
Confidence Intervals and Statistical Guidelines. John Wiley & Sons.
Williamson, R., Boardman, S., Eaton, G., Graham, T. & Parramore, K., 2010. Statistics.
Oxford: Hienemann.

Appendix
Calculations for Question 1
Note: The procedure below is used:
a) if population standard deviation is unknown and sample size is at least 30;
Or
b) if sample size is less than 30 and underlying population is approximately normal.
For Rhode Island Red Eggs
Step 1: Find α/2
Level of Confidence = 99%
α = 100% - (Level of Confidence) = 1%
α/2 = 0.5% = 0.005
Step 2: Find tα/2
Calculate tα/2 by using t-distribution with degrees of freedom (DF) as n - 1 = 50 - 1 = 49 and
α/2 = 0.005 as right-tailed area and left-tailed area.
tα/2 = 2.679952
Step 3: Calculate Confidence Interval
Given x̄ = 39.3576, s = 8.921577, n = 50
Lower Bound = x̄ - tα/2•(s/√n) = 39.3576 - (2.679952)*(8.921577/√50) = 35.976
Upper Bound = x̄ + tα/2•(s/√n) = 39.3576 + (2.679952)*(8.921577/√50) = 42.739
Confidence Interval = (35.976, 42.739)
For Welsomer Eggs
Step 1: Find α/2
Level of Confidence = 99%
α = 100% - (Level of Confidence) = 1%
α/2 = 0.5% = 0.005
Step 2: Find tα/2

Calculate tα/2 by using t-distribution with degrees of freedom (DF) as n - 1 = 50 - 1 = 49 and
α/2 = 0.005 as right-tailed area and left-tailed area.
tα/2 = 2.661759
Step 3: Calculate Confidence Interval
Given x̄ = 52.74, s = 13.99489, n = 60
Lower Bound = x̄ - tα/2•(s/√n) = 52.74 - (2.661759)(13.99489/√60) = 47.931
Upper Bound = x̄ + tα/2•(s/√n) = 52.74 + (2.661759)(13.99489/√60) = 57.549
Confidence Interval = (47.931, 57.549)
For White Leghorn Eggs
Step 1: Find α/2
Level of Confidence = 99%
α = 100% - (Level of Confidence) = 1%
α/2 = 0.5% = 0.005
Step 2: Find tα/2
Calculate tα/2 by using t-distribution with degrees of freedom (DF) as n - 1 = 50 - 1 = 49 and
α/2 = 0.005 as right-tailed area and left-tailed area.
tα/2 = 2.661759
Step 3: Calculate Confidence Interval
Given x̄ = 44.08117, s = 14.83701, n = 60
Lower Bound = x̄ - tα/2•(s/√n) = 44.08117 - (2.661759)(14.83701/√60) = 38.983
Upper Bound = x̄ + tα/2•(s/√n) = 44.08117 + (2.661759)(14.83701/√60) = 49.180
Confidence Interval = (38.983, 49.180)
Calculations for Question 2
Lighter Cows
Step 1: Find α/2
Level of Confidence = 99%
α = 100% - (Level of Confidence) = 1%

α/2 = 0.5% = 0.005
Step 2: Find tα/2
Calculate tα/2 by using t-distribution with degrees of freedom (DF) as n - 1 = 50 - 1 = 49 and
α/2 = 0.005 as right-tailed area and left-tailed area.
tα/2 = 2.679952
Step 3: Calculate Confidence Interval
Given x̄ = 3.5996, s = 2.5667, n = 50
Lower Bound = x̄ - tα/2•(s/√n) = 3.5996 - (2.679952)(2.5667/√50) = 2.627
Upper Bound = x̄ + tα/2•(s/√n) = 3.5996 + (2.679952)(2.5667/√50) = 4.572
Confidence Interval = (2.627, 4.572)
Heavier Cows
Step 1: Find α/2
Level of Confidence = 99%
α = 100% - (Level of Confidence) = 1%
α/2 = 0.5% = 0.005
Step 2: Find tα/2
Calculate tα/2 by using t-distribution with degrees of freedom (DF) as n - 1 = 50 - 1 = 49 and
α/2 = 0.005 as right-tailed area and left-tailed area.
tα/2 = 2.648977
Step 3: Calculate Confidence Interval
Given x̄ = 7.9324, s = 3.7893, n = 70
Lower Bound = x̄ - tα/2•(s/√n) = 7.9324 - (2.648977)(3.7893/√70) = 6.733
Upper Bound = x̄ + tα/2•(s/√n) = 7.9324 + (2.648977)(3.7893/√70) = 9.132
Confidence Interval = (6.733, 9.132)