Business Finance: CAPM, Project Analysis, and Yield Curve Analysis
VerifiedAdded on 2020/04/07
|12
|2309
|226
Homework Assignment
AI Summary
This finance assignment provides a comprehensive analysis of various financial concepts. It begins with an application of the Capital Asset Pricing Model (CAPM) to evaluate stock valuations, considering beta and market risk. The assignment then delves into capital budgeting, evaluating projects using methods such as Net Present Value (NPV), payback period, profitability index, and Internal Rate of Return (IRR). Furthermore, it explores loan calculations, including annual repayments and total interest paid over different loan terms. The assignment also examines yield curve analysis, comparing different yield curve patterns and applying the expectations theory to predict interest rates. Finally, it analyzes the spread between Australian Government and NSW Treasury bonds across different maturities.

Business Finance
[Type the abstract of the document here. The abstract is typically a short summary of the contents
of the document. Type the abstract of the document here. The abstract is typically a short
summary of the contents of the document.]
[Type the abstract of the document here. The abstract is typically a short summary of the contents
of the document. Type the abstract of the document here. The abstract is typically a short
summary of the contents of the document.]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Question 1
a) Expected return on a share = Rf + ß (Rm - Rf )
Share Risk free
rate (Rf)
Market risk
premium(Rm - Rf )
Beta E(r)
using
CAPM
Expected
return of
investor
Comment
A 3% (8%-3%) = 5% 1.5 10.5% 14% Overvalued
B 3% (8%-3%) = 5% 0.6 6% 8% Overvalued
C 3% (8%-3%) = 5% 1.2 9% 9% Correctly
priced
D 3% (8%-3%) = 5% 1.8 12% 10% Undervalued
b) Beta of a share measures its sensitivity to the market. A beta of 1 means the share is as
volatile as the market and moves in tandem with the market. A beta of more than 1 means the
share is very volatile and with an increase in market returns, the returns of the share will
increase by more than the market and vice versa. However, when we consider a portfolio of
stocks, it is better to have low beta stocks in the portfolio because low beat stocks have more
or less stable price and their return also increase gradually in the form of dividend income.
Thus low beta stocks will be able to outperform a portfolio of high beta stocks (Jim,
2011)Hence, in the above case, a portfolio of stocks A and B who have low beta as compared
to D will outperform the individual returns from stock D.
c) The table of incremental cash flows for each project A, B and C is given below:
Project A
Year Cash flows PV
Present value of
cash flows
0 -20,000 1 -20,000
1 18,000 0.893 16,071
2 18,000 0.797 14,349
3 18,000 0.712 12,812
NPV 23,233
a) Expected return on a share = Rf + ß (Rm - Rf )
Share Risk free
rate (Rf)
Market risk
premium(Rm - Rf )
Beta E(r)
using
CAPM
Expected
return of
investor
Comment
A 3% (8%-3%) = 5% 1.5 10.5% 14% Overvalued
B 3% (8%-3%) = 5% 0.6 6% 8% Overvalued
C 3% (8%-3%) = 5% 1.2 9% 9% Correctly
priced
D 3% (8%-3%) = 5% 1.8 12% 10% Undervalued
b) Beta of a share measures its sensitivity to the market. A beta of 1 means the share is as
volatile as the market and moves in tandem with the market. A beta of more than 1 means the
share is very volatile and with an increase in market returns, the returns of the share will
increase by more than the market and vice versa. However, when we consider a portfolio of
stocks, it is better to have low beta stocks in the portfolio because low beat stocks have more
or less stable price and their return also increase gradually in the form of dividend income.
Thus low beta stocks will be able to outperform a portfolio of high beta stocks (Jim,
2011)Hence, in the above case, a portfolio of stocks A and B who have low beta as compared
to D will outperform the individual returns from stock D.
c) The table of incremental cash flows for each project A, B and C is given below:
Project A
Year Cash flows PV
Present value of
cash flows
0 -20,000 1 -20,000
1 18,000 0.893 16,071
2 18,000 0.797 14,349
3 18,000 0.712 12,812
NPV 23,233
Project B
Year Cash flows PV
Present value of
cash flows
0 -40,000 1 -40,000
1 5,000 0.893 4,464
2 10,000 0.797 7,972
3 30,000 0.712 21,353
4 80,000 0.636 50,841
5 1,00,000 0.567 56,743
NPV 1,01,374
Project C
Year Cash flows PV
Present value of
cash flows
0 -70,000 1 -70,000
1 30,000 0.893 26,786
2 30,000 0.797 23,916
3 40,000 0.712 28,471
4 50,000 0.636 31,776
5 1,80,000 0.567 1,02,137
NPV 1,43,085
Ranking of projects
Project NPV Rank
A $23,233 3
B $1,01,374 2
C $1,43,085 1
d) Payback period of the projects
Project A
Year Cash flow Cumulative cash flow
0 -20,000 -20,000
1 18,000 -2,000
2 18,000 16,000
3 18,000 34,000
Year Cash flows PV
Present value of
cash flows
0 -40,000 1 -40,000
1 5,000 0.893 4,464
2 10,000 0.797 7,972
3 30,000 0.712 21,353
4 80,000 0.636 50,841
5 1,00,000 0.567 56,743
NPV 1,01,374
Project C
Year Cash flows PV
Present value of
cash flows
0 -70,000 1 -70,000
1 30,000 0.893 26,786
2 30,000 0.797 23,916
3 40,000 0.712 28,471
4 50,000 0.636 31,776
5 1,80,000 0.567 1,02,137
NPV 1,43,085
Ranking of projects
Project NPV Rank
A $23,233 3
B $1,01,374 2
C $1,43,085 1
d) Payback period of the projects
Project A
Year Cash flow Cumulative cash flow
0 -20,000 -20,000
1 18,000 -2,000
2 18,000 16,000
3 18,000 34,000
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Payback period = 1+ (2000/18000)
= 1.11 years
Project B
Year Cash flow Cumulative cash flow
0 -40,000 -40,000
1 5,000 -35,000
2 10,000 -25,000
3 30,000 5,000
4 80,000 85,000
5 1,00,000 1,85,000
Payback period = 2+ (25000/30000)
= 2.83 years
Project C
Year Cash flow Cumulative cash flow
0 -70,000 -70,000
1 30,000 -40,000
2 30,000 -10,000
3 40,000 30,000
4 50,000 80,000
5 1,80,000 2,60,000
Payback period = 2+ (10000/40000)
= 2.25 years
Since the acceptable payback period is 2.75 years or less, we can accept projects A and C
which have payback periods less than 2.75 years.
e) Profitability index
Profitability index = PV of future cash flows / initial investment
Project PV of future cash flows Initial investment PI
A 43,233 20,000 2.2
= 1.11 years
Project B
Year Cash flow Cumulative cash flow
0 -40,000 -40,000
1 5,000 -35,000
2 10,000 -25,000
3 30,000 5,000
4 80,000 85,000
5 1,00,000 1,85,000
Payback period = 2+ (25000/30000)
= 2.83 years
Project C
Year Cash flow Cumulative cash flow
0 -70,000 -70,000
1 30,000 -40,000
2 30,000 -10,000
3 40,000 30,000
4 50,000 80,000
5 1,80,000 2,60,000
Payback period = 2+ (10000/40000)
= 2.25 years
Since the acceptable payback period is 2.75 years or less, we can accept projects A and C
which have payback periods less than 2.75 years.
e) Profitability index
Profitability index = PV of future cash flows / initial investment
Project PV of future cash flows Initial investment PI
A 43,233 20,000 2.2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

B 141,374 40,000 3.5
C 213,086 70,000 3
Internal rate of return
Project IRR
A 72%
B 56%
C 56%
Question 2
a) Cost of house = $700000, cash payment = $70000, loan = $630000, interest rate = 3.5%
Annual repayment of loan = = r (P) / (1-(1+r)-n)
Annual repayment of 20 year loan = 3.5%*630000 / (1-(1+0.035)-20)
= $44,327
Annual repayment of 25 year loan = 3.5%*630000 / (1-(1+0.035)-25)
= $38,225
The annual repayment of 20 year loan is more than the annual repayment of 25 year loan.
b) Total interest paid on 20 year loan = (44327*20) - 630000
= $256,540
Total interest paid on 25 year loan = (38225*25) - 630000
= $325,625
c) With an increase in the loan period, the annual repayment decreases. The loan instalment
for 20 year loan is more than the 25 year loan.
C 213,086 70,000 3
Internal rate of return
Project IRR
A 72%
B 56%
C 56%
Question 2
a) Cost of house = $700000, cash payment = $70000, loan = $630000, interest rate = 3.5%
Annual repayment of loan = = r (P) / (1-(1+r)-n)
Annual repayment of 20 year loan = 3.5%*630000 / (1-(1+0.035)-20)
= $44,327
Annual repayment of 25 year loan = 3.5%*630000 / (1-(1+0.035)-25)
= $38,225
The annual repayment of 20 year loan is more than the annual repayment of 25 year loan.
b) Total interest paid on 20 year loan = (44327*20) - 630000
= $256,540
Total interest paid on 25 year loan = (38225*25) - 630000
= $325,625
c) With an increase in the loan period, the annual repayment decreases. The loan instalment
for 20 year loan is more than the 25 year loan.
With an increase in the loan term, the total interest also increases as interest is paid for larger
number of periods.
d) New interest rate from 2021 onwards = 6%
Annual loan repayment from 2021 for 20 year loan = (6%*630000) / (1-(1+0.06)-17)
= $60,132
Annual loan repayment from 2021 for 25 year loan = (65*630000) / (1-(1+0.06)-22)
= $52,319
Question 3
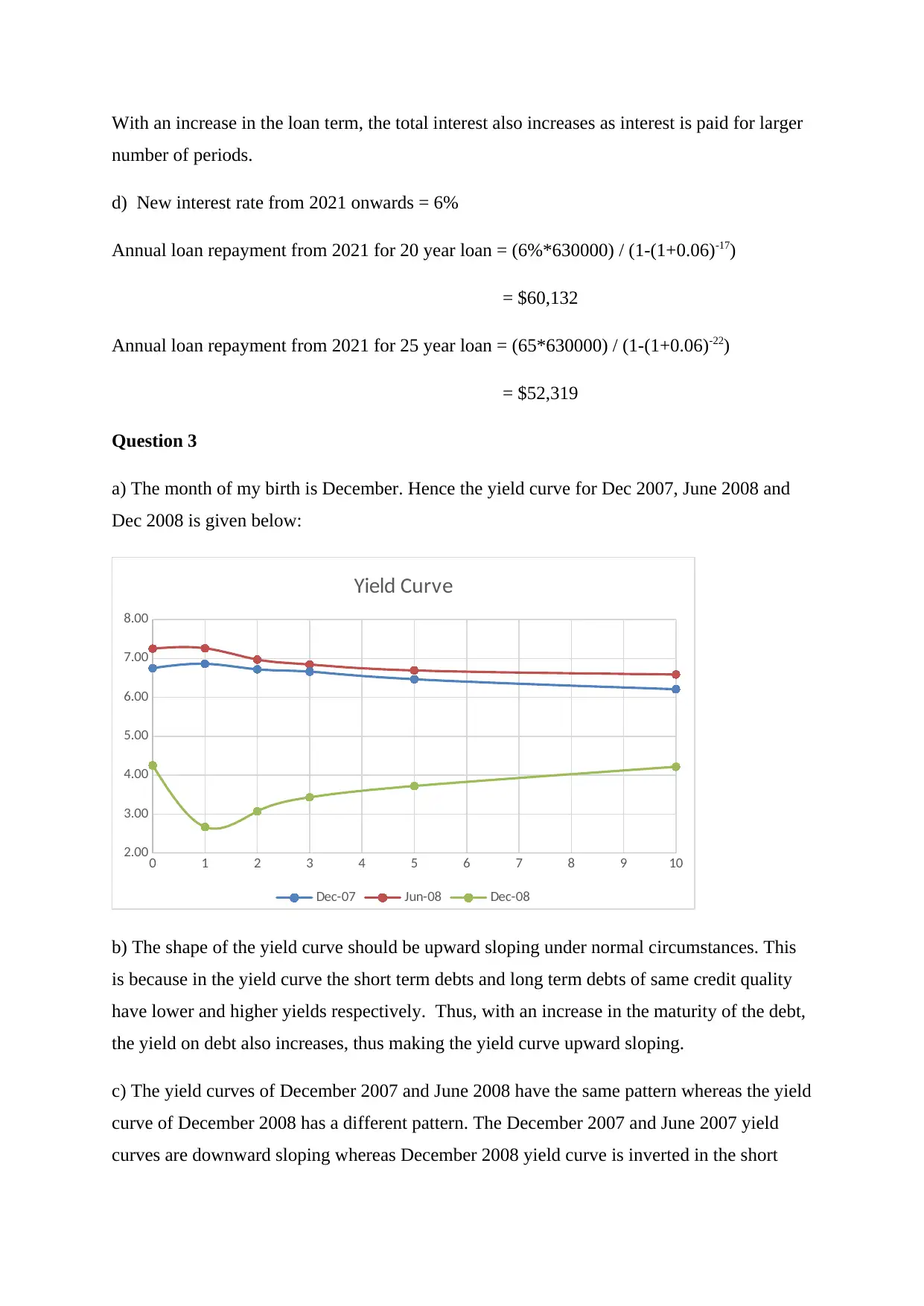
a) The month of my birth is December. Hence the yield curve for Dec 2007, June 2008 and
Dec 2008 is given below:
0 1 2 3 4 5 6 7 8 9 10
2.00
3.00
4.00
5.00
6.00
7.00
8.00
Yield Curve
Dec-07 Jun-08 Dec-08
b) The shape of the yield curve should be upward sloping under normal circumstances. This
is because in the yield curve the short term debts and long term debts of same credit quality
have lower and higher yields respectively. Thus, with an increase in the maturity of the debt,
the yield on debt also increases, thus making the yield curve upward sloping.
c) The yield curves of December 2007 and June 2008 have the same pattern whereas the yield
curve of December 2008 has a different pattern. The December 2007 and June 2007 yield
curves are downward sloping whereas December 2008 yield curve is inverted in the short
number of periods.
d) New interest rate from 2021 onwards = 6%
Annual loan repayment from 2021 for 20 year loan = (6%*630000) / (1-(1+0.06)-17)
= $60,132
Annual loan repayment from 2021 for 25 year loan = (65*630000) / (1-(1+0.06)-22)
= $52,319
Question 3
a) The month of my birth is December. Hence the yield curve for Dec 2007, June 2008 and
Dec 2008 is given below:
0 1 2 3 4 5 6 7 8 9 10
2.00
3.00
4.00
5.00
6.00
7.00
8.00
Yield Curve
Dec-07 Jun-08 Dec-08
b) The shape of the yield curve should be upward sloping under normal circumstances. This
is because in the yield curve the short term debts and long term debts of same credit quality
have lower and higher yields respectively. Thus, with an increase in the maturity of the debt,
the yield on debt also increases, thus making the yield curve upward sloping.
c) The yield curves of December 2007 and June 2008 have the same pattern whereas the yield
curve of December 2008 has a different pattern. The December 2007 and June 2007 yield
curves are downward sloping whereas December 2008 yield curve is inverted in the short
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

term and thereafter upward sloping. The December 2007 and June 2007 yield curves are
negative yield curves and suggest that with increasing bonds maturity, the yield is falling.
The yield curves give an idea as to the economic activity of an economy and also its future
inflation (Kerkhoff, 2015) The December 2007 yield curve is upward sloping for 1 year
which means that the interest rates will rise and economy will grow next year. However,
thereafter the yields are falling with increase in maturity which means the interest rates will
fall in the future after 1 year slowing down the economy. The slowdown will be higher
between 5 years to 10 years. As per the June 2007 yield curve, the economy will grow rapidly
for the next 1 year with high increase in interest rate. Thereafter the economy will slow down
at a low rate for the next 5 years. Thereafter the slowdown will be high as the interest rate
will fall by a higher percentage. The December 2008 yield curve is inverted for next 1 year
showing slow economic activity. Thereafter the economy is expected to grow at a fast pace
for the next 10 years as the yield is increasing with increasing maturity.
d) According to the monthly data on yields on Australian Government Bonds, the yield on 2
year bond in Jan 2007 is 6.18%.
The interest rate investors expect on a 1-year bond next year (Jan 2008) can be calculated
using the expectations theory.
Yield on 2 year bond in 2007 = 6.18%
First we add 1 to 6.18% which is 1.0618, then we square it which is (1.06182) 1.127.
Yield on 1 year bond in 2007 = 6.26%
To 1.127, we divide 1.0626 = 1.127 / 1.0626 = 1.061
Expected interest rate on 1 year bond next year (Jan 2008) = 1.061-1
= 6.1%
Expected interest rates for all months of 2008 on 1 year bonds using the expectation theory
are given below:
2007
Yield on
2 years
bond
(2007)
Step 1
Yield on 1
year bond
(2007)
Step 2
Expected
rate on 1-
year bond
(2008)
negative yield curves and suggest that with increasing bonds maturity, the yield is falling.
The yield curves give an idea as to the economic activity of an economy and also its future
inflation (Kerkhoff, 2015) The December 2007 yield curve is upward sloping for 1 year
which means that the interest rates will rise and economy will grow next year. However,
thereafter the yields are falling with increase in maturity which means the interest rates will
fall in the future after 1 year slowing down the economy. The slowdown will be higher
between 5 years to 10 years. As per the June 2007 yield curve, the economy will grow rapidly
for the next 1 year with high increase in interest rate. Thereafter the economy will slow down
at a low rate for the next 5 years. Thereafter the slowdown will be high as the interest rate
will fall by a higher percentage. The December 2008 yield curve is inverted for next 1 year
showing slow economic activity. Thereafter the economy is expected to grow at a fast pace
for the next 10 years as the yield is increasing with increasing maturity.
d) According to the monthly data on yields on Australian Government Bonds, the yield on 2
year bond in Jan 2007 is 6.18%.
The interest rate investors expect on a 1-year bond next year (Jan 2008) can be calculated
using the expectations theory.
Yield on 2 year bond in 2007 = 6.18%
First we add 1 to 6.18% which is 1.0618, then we square it which is (1.06182) 1.127.
Yield on 1 year bond in 2007 = 6.26%
To 1.127, we divide 1.0626 = 1.127 / 1.0626 = 1.061
Expected interest rate on 1 year bond next year (Jan 2008) = 1.061-1
= 6.1%
Expected interest rates for all months of 2008 on 1 year bonds using the expectation theory
are given below:
2007
Yield on
2 years
bond
(2007)
Step 1
Yield on 1
year bond
(2007)
Step 2
Expected
rate on 1-
year bond
(2008)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
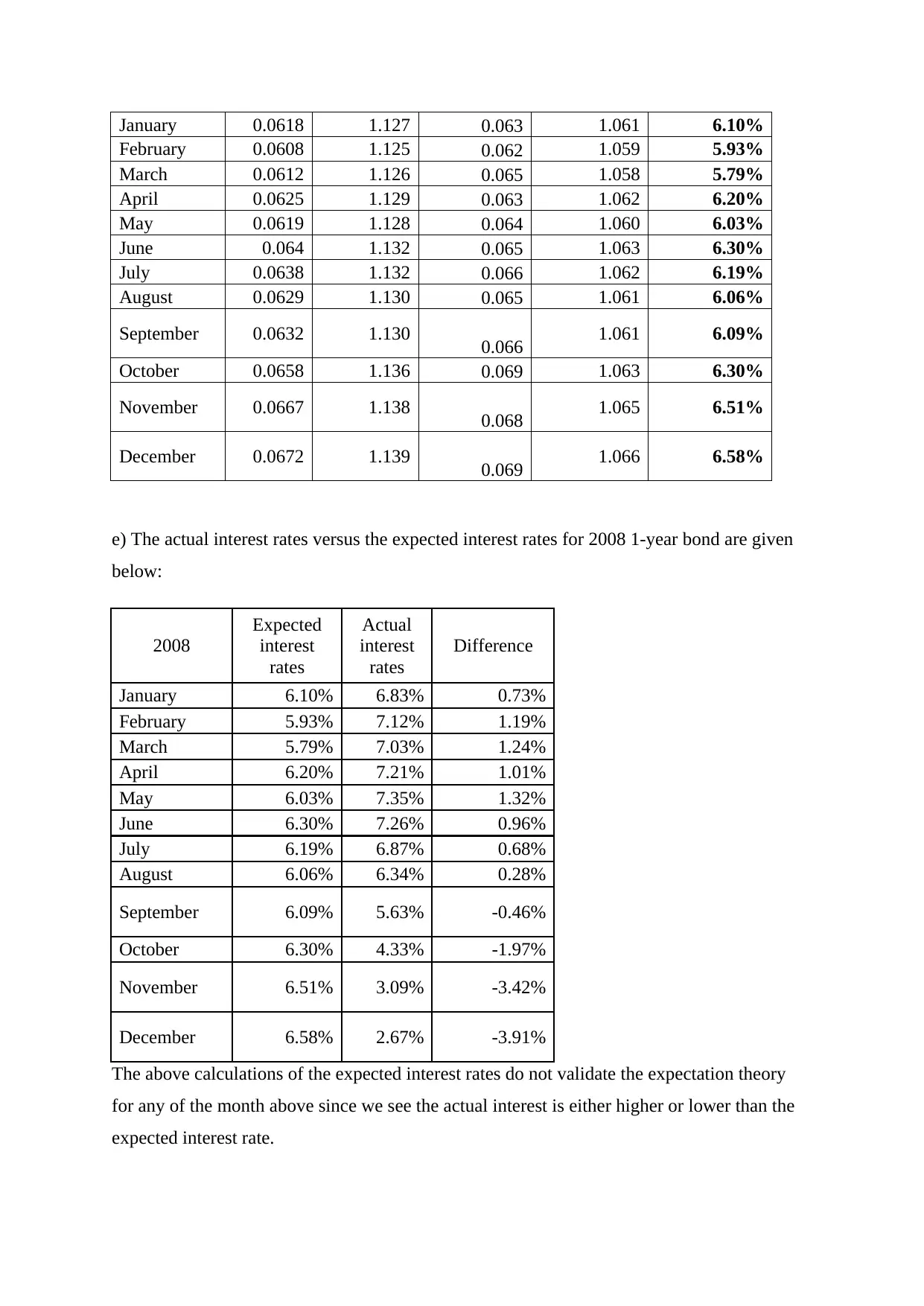
January 0.0618 1.127 0.063 1.061 6.10%
February 0.0608 1.125 0.062 1.059 5.93%
March 0.0612 1.126 0.065 1.058 5.79%
April 0.0625 1.129 0.063 1.062 6.20%
May 0.0619 1.128 0.064 1.060 6.03%
June 0.064 1.132 0.065 1.063 6.30%
July 0.0638 1.132 0.066 1.062 6.19%
August 0.0629 1.130 0.065 1.061 6.06%
September 0.0632 1.130 0.066 1.061 6.09%
October 0.0658 1.136 0.069 1.063 6.30%
November 0.0667 1.138 0.068 1.065 6.51%
December 0.0672 1.139 0.069 1.066 6.58%
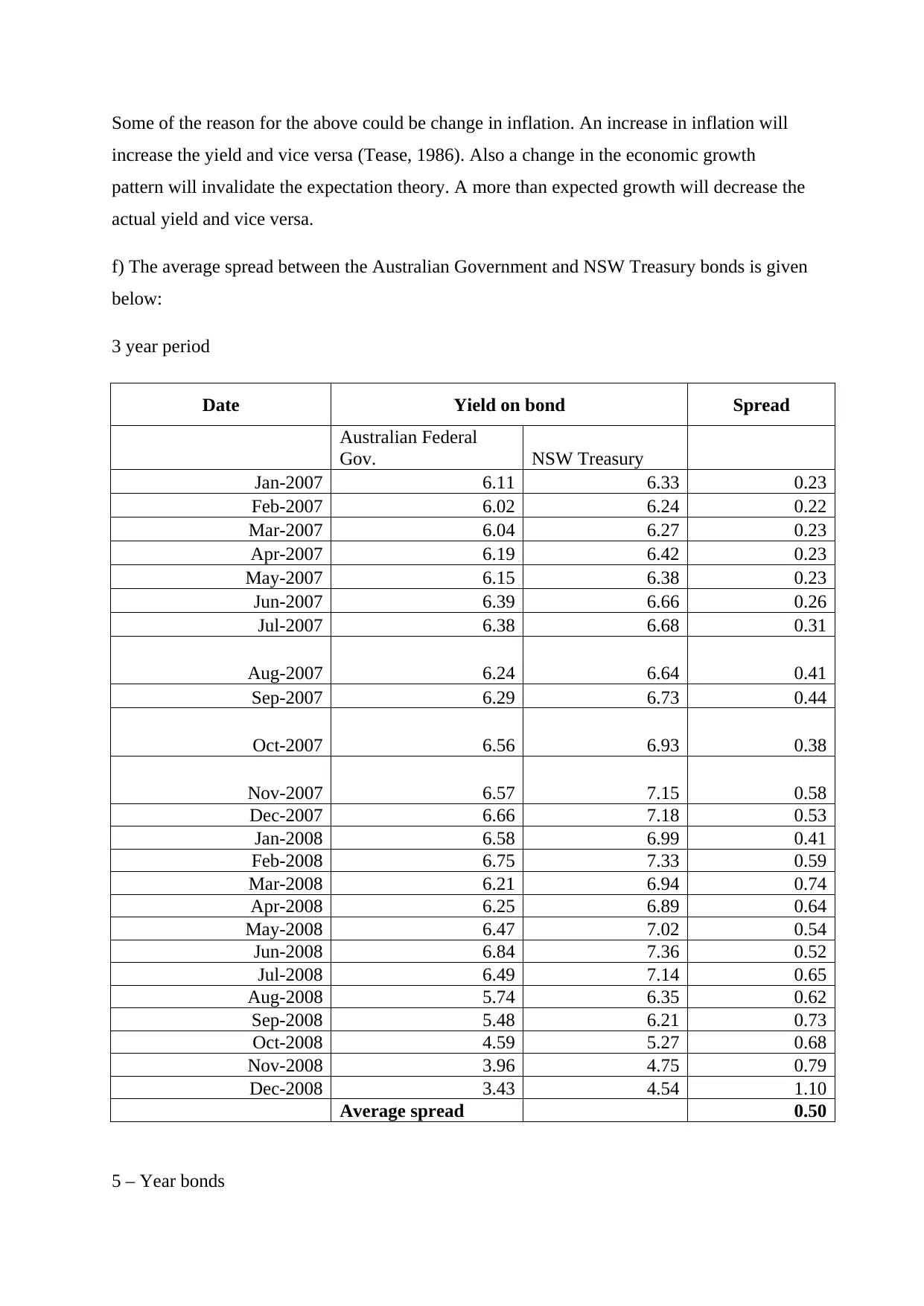
e) The actual interest rates versus the expected interest rates for 2008 1-year bond are given
below:
2008
Expected
interest
rates
Actual
interest
rates
Difference
January 6.10% 6.83% 0.73%
February 5.93% 7.12% 1.19%
March 5.79% 7.03% 1.24%
April 6.20% 7.21% 1.01%
May 6.03% 7.35% 1.32%
June 6.30% 7.26% 0.96%
July 6.19% 6.87% 0.68%
August 6.06% 6.34% 0.28%
September 6.09% 5.63% -0.46%
October 6.30% 4.33% -1.97%
November 6.51% 3.09% -3.42%
December 6.58% 2.67% -3.91%
The above calculations of the expected interest rates do not validate the expectation theory
for any of the month above since we see the actual interest is either higher or lower than the
expected interest rate.
February 0.0608 1.125 0.062 1.059 5.93%
March 0.0612 1.126 0.065 1.058 5.79%
April 0.0625 1.129 0.063 1.062 6.20%
May 0.0619 1.128 0.064 1.060 6.03%
June 0.064 1.132 0.065 1.063 6.30%
July 0.0638 1.132 0.066 1.062 6.19%
August 0.0629 1.130 0.065 1.061 6.06%
September 0.0632 1.130 0.066 1.061 6.09%
October 0.0658 1.136 0.069 1.063 6.30%
November 0.0667 1.138 0.068 1.065 6.51%
December 0.0672 1.139 0.069 1.066 6.58%
e) The actual interest rates versus the expected interest rates for 2008 1-year bond are given
below:
2008
Expected
interest
rates
Actual
interest
rates
Difference
January 6.10% 6.83% 0.73%
February 5.93% 7.12% 1.19%
March 5.79% 7.03% 1.24%
April 6.20% 7.21% 1.01%
May 6.03% 7.35% 1.32%
June 6.30% 7.26% 0.96%
July 6.19% 6.87% 0.68%
August 6.06% 6.34% 0.28%
September 6.09% 5.63% -0.46%
October 6.30% 4.33% -1.97%
November 6.51% 3.09% -3.42%
December 6.58% 2.67% -3.91%
The above calculations of the expected interest rates do not validate the expectation theory
for any of the month above since we see the actual interest is either higher or lower than the
expected interest rate.
Some of the reason for the above could be change in inflation. An increase in inflation will
increase the yield and vice versa (Tease, 1986). Also a change in the economic growth
pattern will invalidate the expectation theory. A more than expected growth will decrease the
actual yield and vice versa.
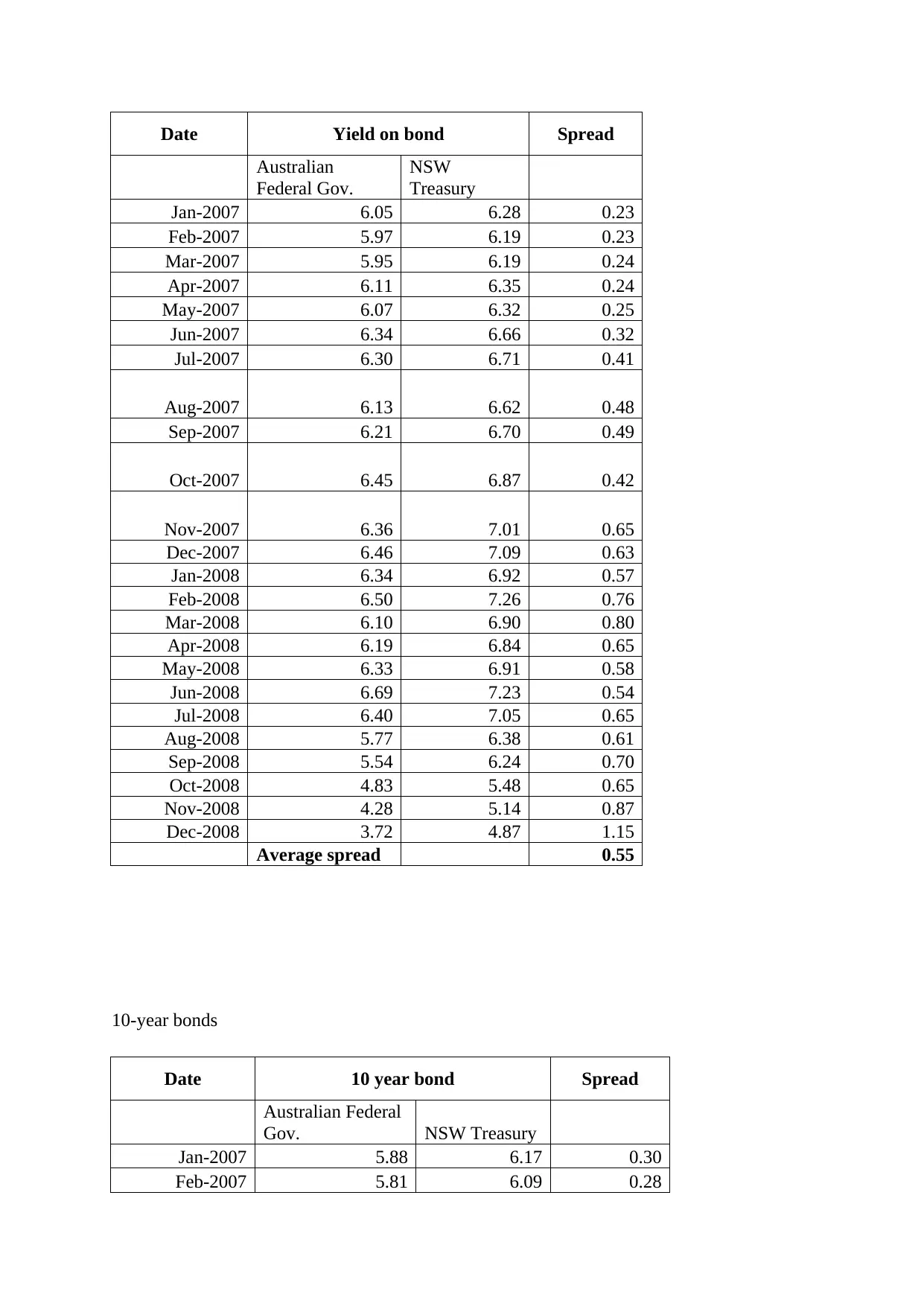
f) The average spread between the Australian Government and NSW Treasury bonds is given
below:
3 year period
Date Yield on bond Spread
Australian Federal
Gov. NSW Treasury
Jan-2007 6.11 6.33 0.23
Feb-2007 6.02 6.24 0.22
Mar-2007 6.04 6.27 0.23
Apr-2007 6.19 6.42 0.23
May-2007 6.15 6.38 0.23
Jun-2007 6.39 6.66 0.26
Jul-2007 6.38 6.68 0.31
Aug-2007 6.24 6.64 0.41
Sep-2007 6.29 6.73 0.44
Oct-2007 6.56 6.93 0.38
Nov-2007 6.57 7.15 0.58
Dec-2007 6.66 7.18 0.53
Jan-2008 6.58 6.99 0.41
Feb-2008 6.75 7.33 0.59
Mar-2008 6.21 6.94 0.74
Apr-2008 6.25 6.89 0.64
May-2008 6.47 7.02 0.54
Jun-2008 6.84 7.36 0.52
Jul-2008 6.49 7.14 0.65
Aug-2008 5.74 6.35 0.62
Sep-2008 5.48 6.21 0.73
Oct-2008 4.59 5.27 0.68
Nov-2008 3.96 4.75 0.79
Dec-2008 3.43 4.54 1.10
Average spread 0.50
5 – Year bonds
increase the yield and vice versa (Tease, 1986). Also a change in the economic growth
pattern will invalidate the expectation theory. A more than expected growth will decrease the
actual yield and vice versa.
f) The average spread between the Australian Government and NSW Treasury bonds is given
below:
3 year period
Date Yield on bond Spread
Australian Federal
Gov. NSW Treasury
Jan-2007 6.11 6.33 0.23
Feb-2007 6.02 6.24 0.22
Mar-2007 6.04 6.27 0.23
Apr-2007 6.19 6.42 0.23
May-2007 6.15 6.38 0.23
Jun-2007 6.39 6.66 0.26
Jul-2007 6.38 6.68 0.31
Aug-2007 6.24 6.64 0.41
Sep-2007 6.29 6.73 0.44
Oct-2007 6.56 6.93 0.38
Nov-2007 6.57 7.15 0.58
Dec-2007 6.66 7.18 0.53
Jan-2008 6.58 6.99 0.41
Feb-2008 6.75 7.33 0.59
Mar-2008 6.21 6.94 0.74
Apr-2008 6.25 6.89 0.64
May-2008 6.47 7.02 0.54
Jun-2008 6.84 7.36 0.52
Jul-2008 6.49 7.14 0.65
Aug-2008 5.74 6.35 0.62
Sep-2008 5.48 6.21 0.73
Oct-2008 4.59 5.27 0.68
Nov-2008 3.96 4.75 0.79
Dec-2008 3.43 4.54 1.10
Average spread 0.50
5 – Year bonds
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Date Yield on bond Spread
Australian
Federal Gov.
NSW
Treasury
Jan-2007 6.05 6.28 0.23
Feb-2007 5.97 6.19 0.23
Mar-2007 5.95 6.19 0.24
Apr-2007 6.11 6.35 0.24
May-2007 6.07 6.32 0.25
Jun-2007 6.34 6.66 0.32
Jul-2007 6.30 6.71 0.41
Aug-2007 6.13 6.62 0.48
Sep-2007 6.21 6.70 0.49
Oct-2007 6.45 6.87 0.42
Nov-2007 6.36 7.01 0.65
Dec-2007 6.46 7.09 0.63
Jan-2008 6.34 6.92 0.57
Feb-2008 6.50 7.26 0.76
Mar-2008 6.10 6.90 0.80
Apr-2008 6.19 6.84 0.65
May-2008 6.33 6.91 0.58
Jun-2008 6.69 7.23 0.54
Jul-2008 6.40 7.05 0.65
Aug-2008 5.77 6.38 0.61
Sep-2008 5.54 6.24 0.70
Oct-2008 4.83 5.48 0.65
Nov-2008 4.28 5.14 0.87
Dec-2008 3.72 4.87 1.15
Average spread 0.55
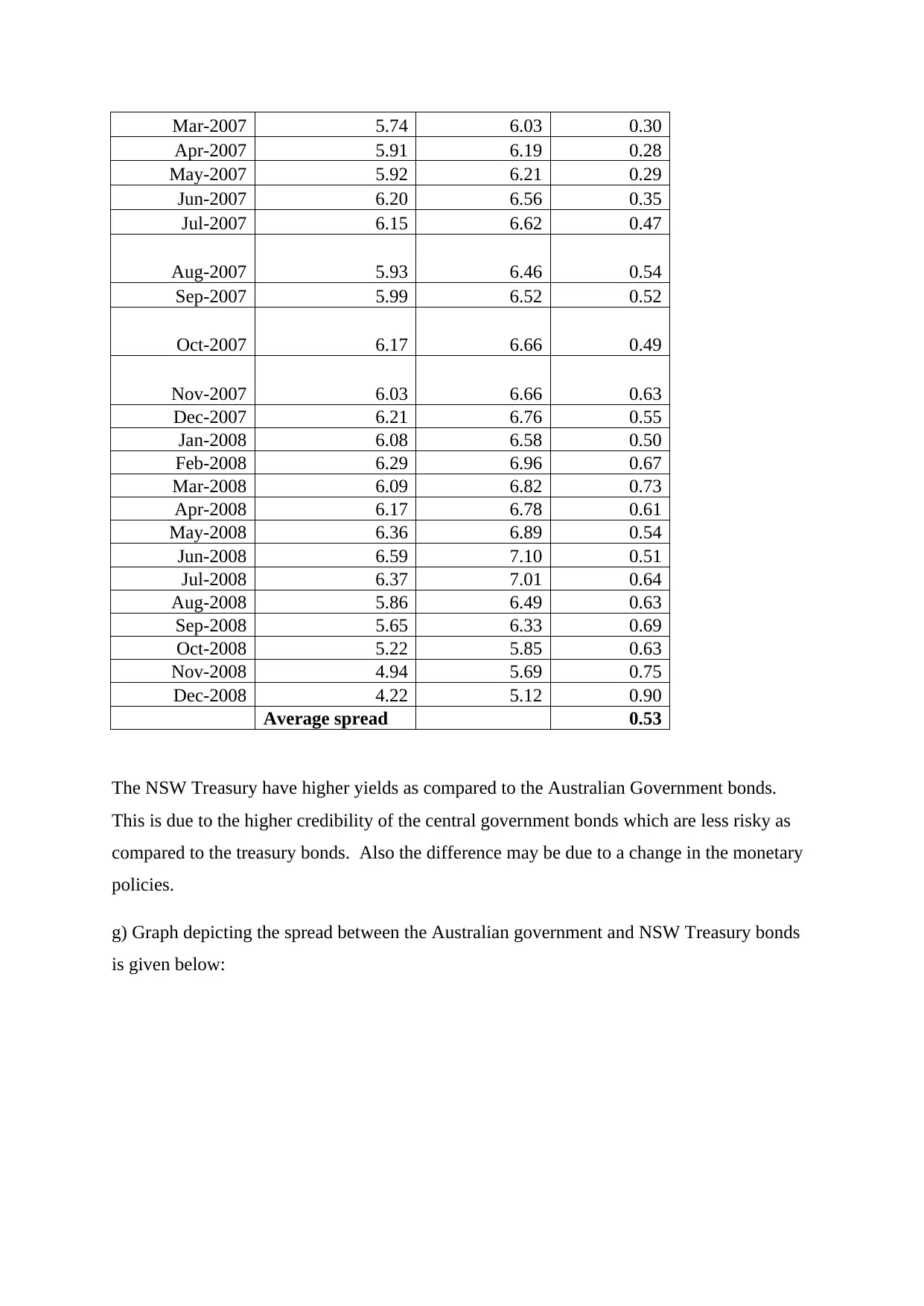
10-year bonds
Date 10 year bond Spread
Australian Federal
Gov. NSW Treasury
Jan-2007 5.88 6.17 0.30
Feb-2007 5.81 6.09 0.28
Australian
Federal Gov.
NSW
Treasury
Jan-2007 6.05 6.28 0.23
Feb-2007 5.97 6.19 0.23
Mar-2007 5.95 6.19 0.24
Apr-2007 6.11 6.35 0.24
May-2007 6.07 6.32 0.25
Jun-2007 6.34 6.66 0.32
Jul-2007 6.30 6.71 0.41
Aug-2007 6.13 6.62 0.48
Sep-2007 6.21 6.70 0.49
Oct-2007 6.45 6.87 0.42
Nov-2007 6.36 7.01 0.65
Dec-2007 6.46 7.09 0.63
Jan-2008 6.34 6.92 0.57
Feb-2008 6.50 7.26 0.76
Mar-2008 6.10 6.90 0.80
Apr-2008 6.19 6.84 0.65
May-2008 6.33 6.91 0.58
Jun-2008 6.69 7.23 0.54
Jul-2008 6.40 7.05 0.65
Aug-2008 5.77 6.38 0.61
Sep-2008 5.54 6.24 0.70
Oct-2008 4.83 5.48 0.65
Nov-2008 4.28 5.14 0.87
Dec-2008 3.72 4.87 1.15
Average spread 0.55
10-year bonds
Date 10 year bond Spread
Australian Federal
Gov. NSW Treasury
Jan-2007 5.88 6.17 0.30
Feb-2007 5.81 6.09 0.28
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Mar-2007 5.74 6.03 0.30
Apr-2007 5.91 6.19 0.28
May-2007 5.92 6.21 0.29
Jun-2007 6.20 6.56 0.35
Jul-2007 6.15 6.62 0.47
Aug-2007 5.93 6.46 0.54
Sep-2007 5.99 6.52 0.52
Oct-2007 6.17 6.66 0.49
Nov-2007 6.03 6.66 0.63
Dec-2007 6.21 6.76 0.55
Jan-2008 6.08 6.58 0.50
Feb-2008 6.29 6.96 0.67
Mar-2008 6.09 6.82 0.73
Apr-2008 6.17 6.78 0.61
May-2008 6.36 6.89 0.54
Jun-2008 6.59 7.10 0.51
Jul-2008 6.37 7.01 0.64
Aug-2008 5.86 6.49 0.63
Sep-2008 5.65 6.33 0.69
Oct-2008 5.22 5.85 0.63
Nov-2008 4.94 5.69 0.75
Dec-2008 4.22 5.12 0.90
Average spread 0.53
The NSW Treasury have higher yields as compared to the Australian Government bonds.
This is due to the higher credibility of the central government bonds which are less risky as
compared to the treasury bonds. Also the difference may be due to a change in the monetary
policies.
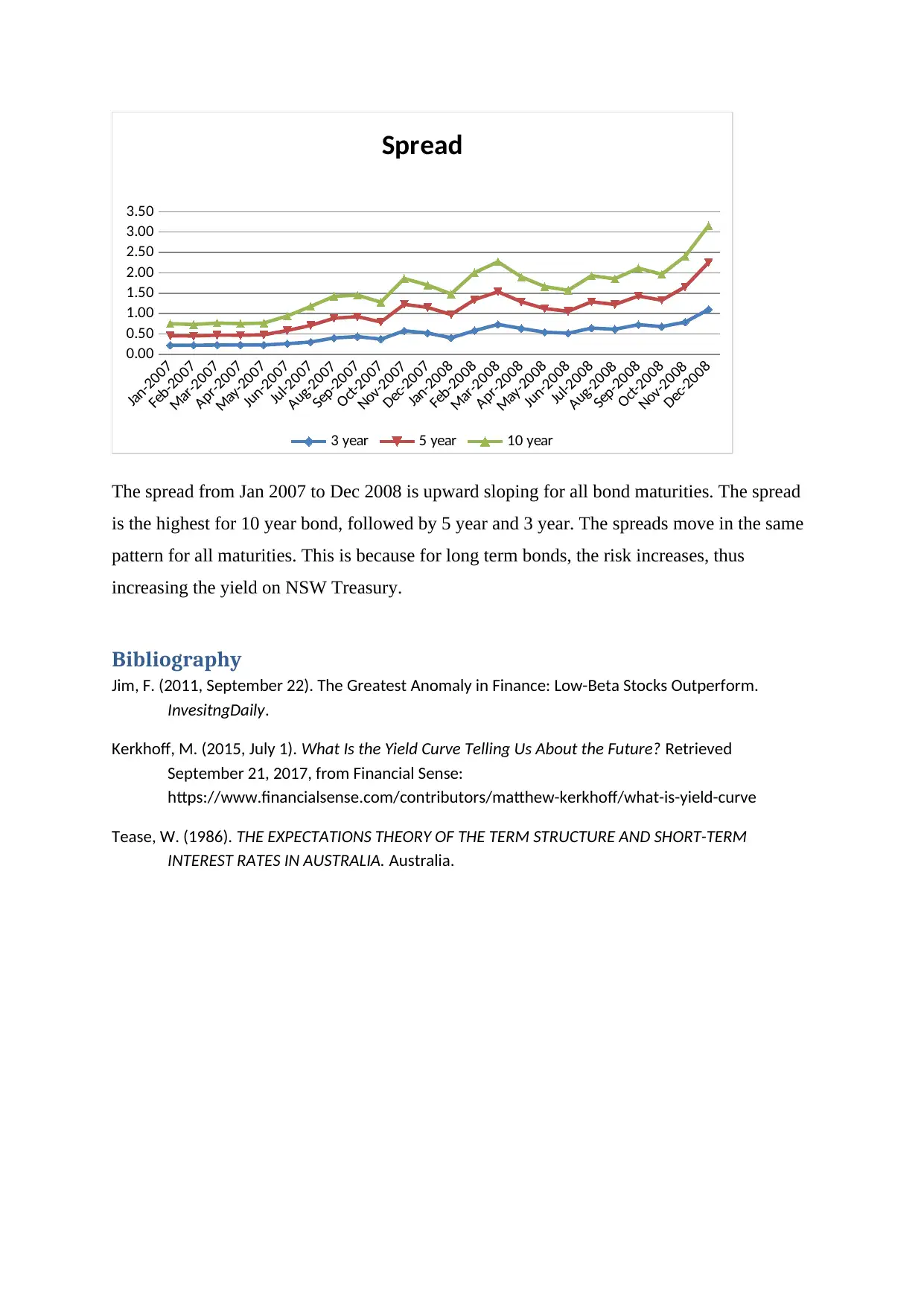
g) Graph depicting the spread between the Australian government and NSW Treasury bonds
is given below:
Apr-2007 5.91 6.19 0.28
May-2007 5.92 6.21 0.29
Jun-2007 6.20 6.56 0.35
Jul-2007 6.15 6.62 0.47
Aug-2007 5.93 6.46 0.54
Sep-2007 5.99 6.52 0.52
Oct-2007 6.17 6.66 0.49
Nov-2007 6.03 6.66 0.63
Dec-2007 6.21 6.76 0.55
Jan-2008 6.08 6.58 0.50
Feb-2008 6.29 6.96 0.67
Mar-2008 6.09 6.82 0.73
Apr-2008 6.17 6.78 0.61
May-2008 6.36 6.89 0.54
Jun-2008 6.59 7.10 0.51
Jul-2008 6.37 7.01 0.64
Aug-2008 5.86 6.49 0.63
Sep-2008 5.65 6.33 0.69
Oct-2008 5.22 5.85 0.63
Nov-2008 4.94 5.69 0.75
Dec-2008 4.22 5.12 0.90
Average spread 0.53
The NSW Treasury have higher yields as compared to the Australian Government bonds.
This is due to the higher credibility of the central government bonds which are less risky as
compared to the treasury bonds. Also the difference may be due to a change in the monetary
policies.
g) Graph depicting the spread between the Australian government and NSW Treasury bonds
is given below:
Jan-2007
Feb-2007
Mar-2007
Apr-2007
May-2007
Jun-2007
Jul-2007
Aug-2007
Sep-2007
Oct-2007
Nov-2007
Dec-2007
Jan-2008
Feb-2008
Mar-2008
Apr-2008
May-2008
Jun-2008
Jul-2008
Aug-2008
Sep-2008
Oct-2008
Nov-2008
Dec-2008
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
Spread
3 year 5 year 10 year
The spread from Jan 2007 to Dec 2008 is upward sloping for all bond maturities. The spread
is the highest for 10 year bond, followed by 5 year and 3 year. The spreads move in the same
pattern for all maturities. This is because for long term bonds, the risk increases, thus
increasing the yield on NSW Treasury.
Bibliography
Jim, F. (2011, September 22). The Greatest Anomaly in Finance: Low-Beta Stocks Outperform.
InvesitngDaily.
Kerkhoff, M. (2015, July 1). What Is the Yield Curve Telling Us About the Future? Retrieved
September 21, 2017, from Financial Sense:
https://www.financialsense.com/contributors/matthew-kerkhoff/what-is-yield-curve
Tease, W. (1986). THE EXPECTATIONS THEORY OF THE TERM STRUCTURE AND SHORT-TERM
INTEREST RATES IN AUSTRALIA. Australia.
Feb-2007
Mar-2007
Apr-2007
May-2007
Jun-2007
Jul-2007
Aug-2007
Sep-2007
Oct-2007
Nov-2007
Dec-2007
Jan-2008
Feb-2008
Mar-2008
Apr-2008
May-2008
Jun-2008
Jul-2008
Aug-2008
Sep-2008
Oct-2008
Nov-2008
Dec-2008
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
Spread
3 year 5 year 10 year
The spread from Jan 2007 to Dec 2008 is upward sloping for all bond maturities. The spread
is the highest for 10 year bond, followed by 5 year and 3 year. The spreads move in the same
pattern for all maturities. This is because for long term bonds, the risk increases, thus
increasing the yield on NSW Treasury.
Bibliography
Jim, F. (2011, September 22). The Greatest Anomaly in Finance: Low-Beta Stocks Outperform.
InvesitngDaily.
Kerkhoff, M. (2015, July 1). What Is the Yield Curve Telling Us About the Future? Retrieved
September 21, 2017, from Financial Sense:
https://www.financialsense.com/contributors/matthew-kerkhoff/what-is-yield-curve
Tease, W. (1986). THE EXPECTATIONS THEORY OF THE TERM STRUCTURE AND SHORT-TERM
INTEREST RATES IN AUSTRALIA. Australia.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





