Analyzing Customer Satisfaction and Business Performance Metrics
VerifiedAdded on 2020/04/07
|11
|1850
|39
AI Summary
This assignment presents a comprehensive analysis of various datasets involving customer satisfaction, business performance metrics, rental revenue, and sales strategies. Students will engage in statistical hypothesis testing to assess the validity of claims made about proportions and means within these data sets. The tasks include calculating sampling errors, standardized Z-scores, and probabilities associated with specific hypotheses. By examining customer satisfaction levels from survey responses and analyzing production efficiency, students can determine if claimed values align statistically with observed results. Additionally, they will explore sales performance related to discounts offered, analyze rental revenue fluctuations, and assess the mean monthly rental against a hypothesized value using provided data. Through these exercises, learners will develop skills in applying statistical methods to real-world business scenarios, enhancing their ability to make data-driven decisions.

Business Statistics
Name of the Student
Name of University
Author Note
Name of the Student
Name of University
Author Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Answer to Q1:
Part a:
Sample mean of left handed spatula:
= 3.5123+ 3.5132+ 3.5133+ 3.5127+3.5127+3.5123
6
=21.0765/6
=3.51275
Part b:
Sample mean of left handed corkscrew:
= 2.9834+2.9833+2.9834+ 2.9834+2.9838+2.9837
6
=17.901/6
=2.9835
Part c:
Sample mean of left handed meat tenderizer:
= 3.5213+ 3.5212+ 3.5212+3.5213+ 3.5212+3.5214
6
= 21.1276/6
= 3.521267
Part d:
Sample mean of left handed Cheese Grater:
= 4.0002+4.0003+4.0001+4.0003+4.0002+4.0003
6
=24.0014/6
=4.000233
Answer Q2:
Part a:
Population mean: ∑xi/n
22 22.01 22.01 22.02 21.98
22 22.01 22.01 22 22.01
21.98 21.99 22.01 22.02 22.03
22 21.99 21.97 22 22.01
Part a:
Sample mean of left handed spatula:
= 3.5123+ 3.5132+ 3.5133+ 3.5127+3.5127+3.5123
6
=21.0765/6
=3.51275
Part b:
Sample mean of left handed corkscrew:
= 2.9834+2.9833+2.9834+ 2.9834+2.9838+2.9837
6
=17.901/6
=2.9835
Part c:
Sample mean of left handed meat tenderizer:
= 3.5213+ 3.5212+ 3.5212+3.5213+ 3.5212+3.5214
6
= 21.1276/6
= 3.521267
Part d:
Sample mean of left handed Cheese Grater:
= 4.0002+4.0003+4.0001+4.0003+4.0002+4.0003
6
=24.0014/6
=4.000233
Answer Q2:
Part a:
Population mean: ∑xi/n
22 22.01 22.01 22.02 21.98
22 22.01 22.01 22 22.01
21.98 21.99 22.01 22.02 22.03
22 21.99 21.97 22 22.01
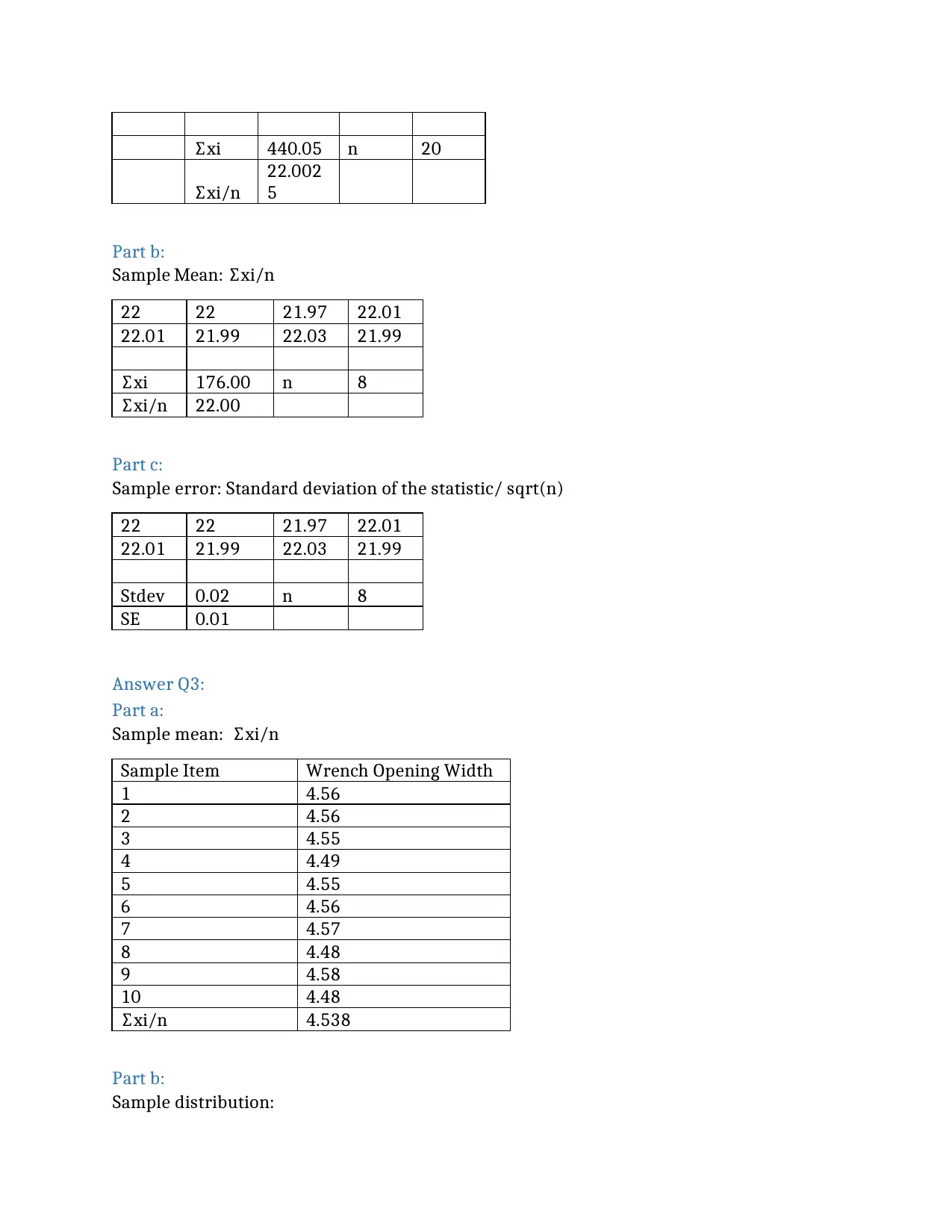
∑xi 440.05 n 20
∑xi/n
22.002
5
Part b:
Sample Mean: ∑xi/n
22 22 21.97 22.01
22.01 21.99 22.03 21.99
∑xi 176.00 n 8
∑xi/n 22.00
Part c:
Sample error: Standard deviation of the statistic/ sqrt(n)
22 22 21.97 22.01
22.01 21.99 22.03 21.99
Stdev 0.02 n 8
SE 0.01
Answer Q3:
Part a:
Sample mean: ∑xi/n
Sample Item Wrench Opening Width
1 4.56
2 4.56
3 4.55
4 4.49
5 4.55
6 4.56
7 4.57
8 4.48
9 4.58
10 4.48
∑xi/n 4.538
Part b:
Sample distribution:
∑xi/n
22.002
5
Part b:
Sample Mean: ∑xi/n
22 22 21.97 22.01
22.01 21.99 22.03 21.99
∑xi 176.00 n 8
∑xi/n 22.00
Part c:
Sample error: Standard deviation of the statistic/ sqrt(n)
22 22 21.97 22.01
22.01 21.99 22.03 21.99
Stdev 0.02 n 8
SE 0.01
Answer Q3:
Part a:
Sample mean: ∑xi/n
Sample Item Wrench Opening Width
1 4.56
2 4.56
3 4.55
4 4.49
5 4.55
6 4.56
7 4.57
8 4.48
9 4.58
10 4.48
∑xi/n 4.538
Part b:
Sample distribution:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

According to the theorem 6-1, the sampling distribution x-bar is defined as μ as center and
σ/sqrt(n) as spread.
Sample Item Wrench Opening Width
1 4.56
2 4.56
3 4.55
4 4.49
5 4.55
6 4.56
7 4.57
8 4.48
9 4.58
10 4.48
shape ( )= ∑xi/nμ 4.538
spread ( /sqrt(n))σ 0.012274635
Part c:
Even of Interest:
Here, the aim is to understand whether the wrench machine needs to be recalibrated or
not. Thus, the event is “Wrench machine needs to be recalibrated.”
Null hypothesis (H0): There is no need for wrench machine recalibration [ >4.56]μ
Alternative hypothesis (H1): There is a need for wrench machine recalibration [ <=4.56]μ
Part d:
Standardized z value: (X-bar – 4.56)/(σ/sqrt(n))
= (4.538-4.56)/( 0.012274635)
=-1.79231
Part e:
Desired probability: 0.0365 = 3.65%
Since, p value is less than 0.05, it can be said that the null hypothesis will be rejected here.
Thus, it can be concluded that there is a need for wrench machine recalibration.
Answer Q4:
Part a:
Sampling distribution: the sampling distribution x-bar is defined as μ as center and
σ/sqrt(n) as spread.
Here, = 32.78μ
= 8.17σ
σ/sqrt(n) as spread.
Sample Item Wrench Opening Width
1 4.56
2 4.56
3 4.55
4 4.49
5 4.55
6 4.56
7 4.57
8 4.48
9 4.58
10 4.48
shape ( )= ∑xi/nμ 4.538
spread ( /sqrt(n))σ 0.012274635
Part c:
Even of Interest:
Here, the aim is to understand whether the wrench machine needs to be recalibrated or
not. Thus, the event is “Wrench machine needs to be recalibrated.”
Null hypothesis (H0): There is no need for wrench machine recalibration [ >4.56]μ
Alternative hypothesis (H1): There is a need for wrench machine recalibration [ <=4.56]μ
Part d:
Standardized z value: (X-bar – 4.56)/(σ/sqrt(n))
= (4.538-4.56)/( 0.012274635)
=-1.79231
Part e:
Desired probability: 0.0365 = 3.65%
Since, p value is less than 0.05, it can be said that the null hypothesis will be rejected here.
Thus, it can be concluded that there is a need for wrench machine recalibration.
Answer Q4:
Part a:
Sampling distribution: the sampling distribution x-bar is defined as μ as center and
σ/sqrt(n) as spread.
Here, = 32.78μ
= 8.17σ
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

And n = 300
Part b:
Let X is the event described in this problem.
Then, X = Amount of mean sales at his store.
Here, the aim is to find out the probability of X, which lies in between 32 and 33
That is P(32 ≤ X ≤ 33)
Part c:
P(32 ≤ X ≤ 33)
= P((32-32.78)/(8.17/sqrt(300)) ≤ Z ≤ (33-32.78)/(8.17/sqrt(300)))
=P(-1.65361 ≤ Z ≤ 0.466403)
= P(Z = 0.466403) – P(z = -1.65361)
= 0.679536 - 0.049103
= 0.630433
= 63.04%
Hence the probability is 63.04% that mean sales at his store will lie in between 32 and 33.
Answer Q5:
Part a:
Population Proportion: The population proportion of blue left handed writing notebook is
0.55
Part b:
Sample proportion: the sample proportion can be calculated as p = 29/60 = 0.4833
Part c:
Sampling error: The sampling error for proportion can be calculated as sqrt(p*(1-p)/n),
where p is the sample proportion and n is the sample size.
Here, p = 0.4833
n = 60
Hence, sampling error = sqrt(0.4833*(1-0.4833)/60) = 0.064514
Answer Q6:
Part a:
Sample proportion:
Here, the sample size (n) is 200 customer.
Part b:
Let X is the event described in this problem.
Then, X = Amount of mean sales at his store.
Here, the aim is to find out the probability of X, which lies in between 32 and 33
That is P(32 ≤ X ≤ 33)
Part c:
P(32 ≤ X ≤ 33)
= P((32-32.78)/(8.17/sqrt(300)) ≤ Z ≤ (33-32.78)/(8.17/sqrt(300)))
=P(-1.65361 ≤ Z ≤ 0.466403)
= P(Z = 0.466403) – P(z = -1.65361)
= 0.679536 - 0.049103
= 0.630433
= 63.04%
Hence the probability is 63.04% that mean sales at his store will lie in between 32 and 33.
Answer Q5:
Part a:
Population Proportion: The population proportion of blue left handed writing notebook is
0.55
Part b:
Sample proportion: the sample proportion can be calculated as p = 29/60 = 0.4833
Part c:
Sampling error: The sampling error for proportion can be calculated as sqrt(p*(1-p)/n),
where p is the sample proportion and n is the sample size.
Here, p = 0.4833
n = 60
Hence, sampling error = sqrt(0.4833*(1-0.4833)/60) = 0.064514
Answer Q6:
Part a:
Sample proportion:
Here, the sample size (n) is 200 customer.

Number of satisfied customer = 189
Therefore, sample proportion of satisfied customer, p = 189/200 = 0.945
Part b:
Mean and standard deviation:
Mean of sampling distribution = p = 0.945
Standard deviation of sampling distribution = sqrt(p*(1-p)/n)
= sqrt(0.945*(1-0.945)/200)
=0.016121
Part c:
Here, the aim is to find out whether Left Behind can put the statement that their customer
service satisfaction rate is 97% or more.
Hence, the event of interest, X is customer satisfaction rate.
In order to claim this following hypothesis can be designed:
H0: Customer satisfaction is less than 97%
H1: Customer satisfaction is greater than or equals to 97%;
Part d:
Here, np = 200*0.945 = 189>5
And np*(1-p) = 189*(1-0.945) = 10>5
Hence the standardized z value of proportion sample is z = (value –mean)/standard
deviation
= (0.97-0.945)/0.01612
= 1.5509
Part e:
Here, the probability of event of interest is P(X>0.97)
=P(Z>1.5509)
= 1 – 0.939533
=0.060467 >0.05
Since, the probability value is more than 0.05, at 95% the null hypothesis is accepted here.
In other words, it can be concluded that Left Behind cannot claim this statement in print
add.
Therefore, sample proportion of satisfied customer, p = 189/200 = 0.945
Part b:
Mean and standard deviation:
Mean of sampling distribution = p = 0.945
Standard deviation of sampling distribution = sqrt(p*(1-p)/n)
= sqrt(0.945*(1-0.945)/200)
=0.016121
Part c:
Here, the aim is to find out whether Left Behind can put the statement that their customer
service satisfaction rate is 97% or more.
Hence, the event of interest, X is customer satisfaction rate.
In order to claim this following hypothesis can be designed:
H0: Customer satisfaction is less than 97%
H1: Customer satisfaction is greater than or equals to 97%;
Part d:
Here, np = 200*0.945 = 189>5
And np*(1-p) = 189*(1-0.945) = 10>5
Hence the standardized z value of proportion sample is z = (value –mean)/standard
deviation
= (0.97-0.945)/0.01612
= 1.5509
Part e:
Here, the probability of event of interest is P(X>0.97)
=P(Z>1.5509)
= 1 – 0.939533
=0.060467 >0.05
Since, the probability value is more than 0.05, at 95% the null hypothesis is accepted here.
In other words, it can be concluded that Left Behind cannot claim this statement in print
add.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
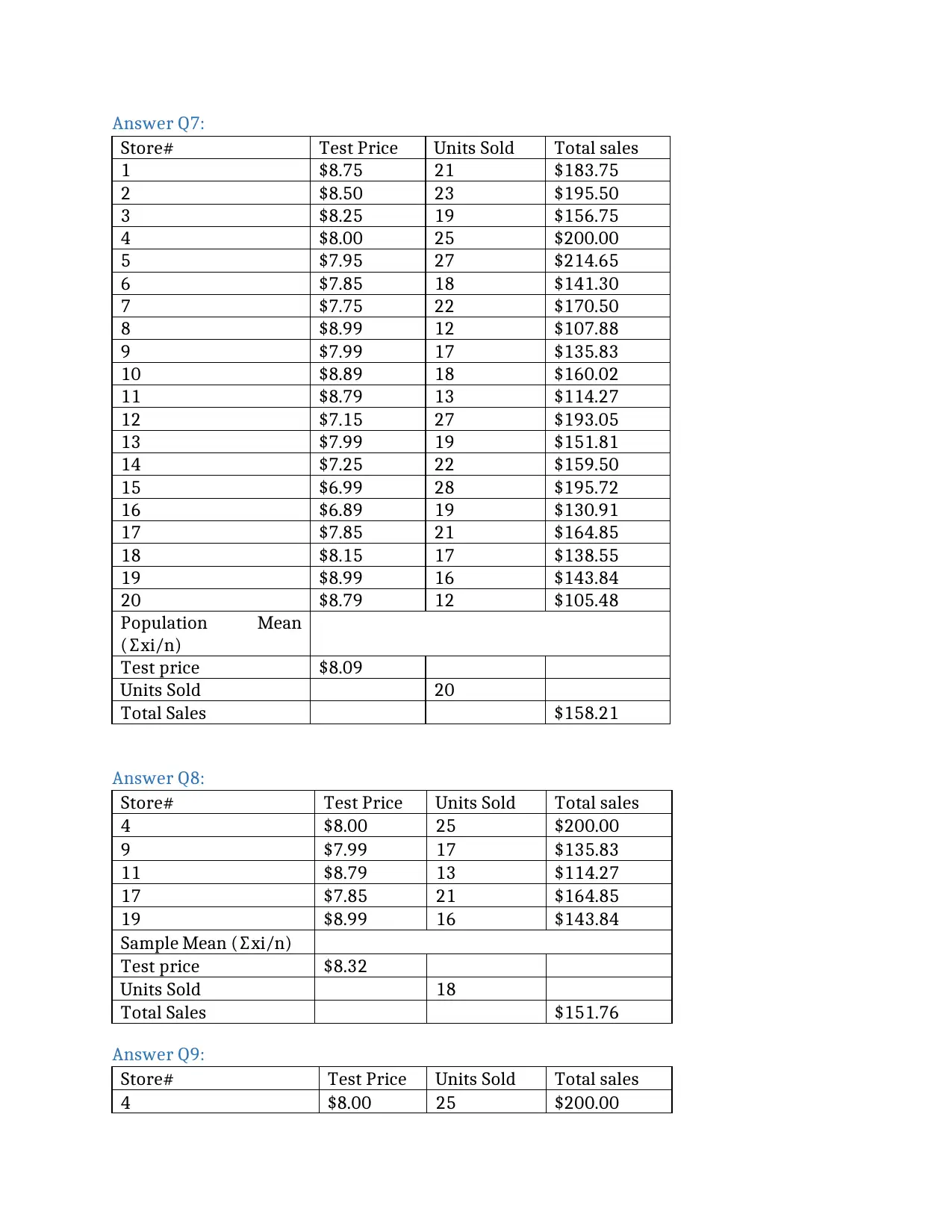
Answer Q7:
Store# Test Price Units Sold Total sales
1 $8.75 21 $183.75
2 $8.50 23 $195.50
3 $8.25 19 $156.75
4 $8.00 25 $200.00
5 $7.95 27 $214.65
6 $7.85 18 $141.30
7 $7.75 22 $170.50
8 $8.99 12 $107.88
9 $7.99 17 $135.83
10 $8.89 18 $160.02
11 $8.79 13 $114.27
12 $7.15 27 $193.05
13 $7.99 19 $151.81
14 $7.25 22 $159.50
15 $6.99 28 $195.72
16 $6.89 19 $130.91
17 $7.85 21 $164.85
18 $8.15 17 $138.55
19 $8.99 16 $143.84
20 $8.79 12 $105.48
Population Mean
(∑xi/n)
Test price $8.09
Units Sold 20
Total Sales $158.21
Answer Q8:
Store# Test Price Units Sold Total sales
4 $8.00 25 $200.00
9 $7.99 17 $135.83
11 $8.79 13 $114.27
17 $7.85 21 $164.85
19 $8.99 16 $143.84
Sample Mean (∑xi/n)
Test price $8.32
Units Sold 18
Total Sales $151.76
Answer Q9:
Store# Test Price Units Sold Total sales
4 $8.00 25 $200.00
Store# Test Price Units Sold Total sales
1 $8.75 21 $183.75
2 $8.50 23 $195.50
3 $8.25 19 $156.75
4 $8.00 25 $200.00
5 $7.95 27 $214.65
6 $7.85 18 $141.30
7 $7.75 22 $170.50
8 $8.99 12 $107.88
9 $7.99 17 $135.83
10 $8.89 18 $160.02
11 $8.79 13 $114.27
12 $7.15 27 $193.05
13 $7.99 19 $151.81
14 $7.25 22 $159.50
15 $6.99 28 $195.72
16 $6.89 19 $130.91
17 $7.85 21 $164.85
18 $8.15 17 $138.55
19 $8.99 16 $143.84
20 $8.79 12 $105.48
Population Mean
(∑xi/n)
Test price $8.09
Units Sold 20
Total Sales $158.21
Answer Q8:
Store# Test Price Units Sold Total sales
4 $8.00 25 $200.00
9 $7.99 17 $135.83
11 $8.79 13 $114.27
17 $7.85 21 $164.85
19 $8.99 16 $143.84
Sample Mean (∑xi/n)
Test price $8.32
Units Sold 18
Total Sales $151.76
Answer Q9:
Store# Test Price Units Sold Total sales
4 $8.00 25 $200.00
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
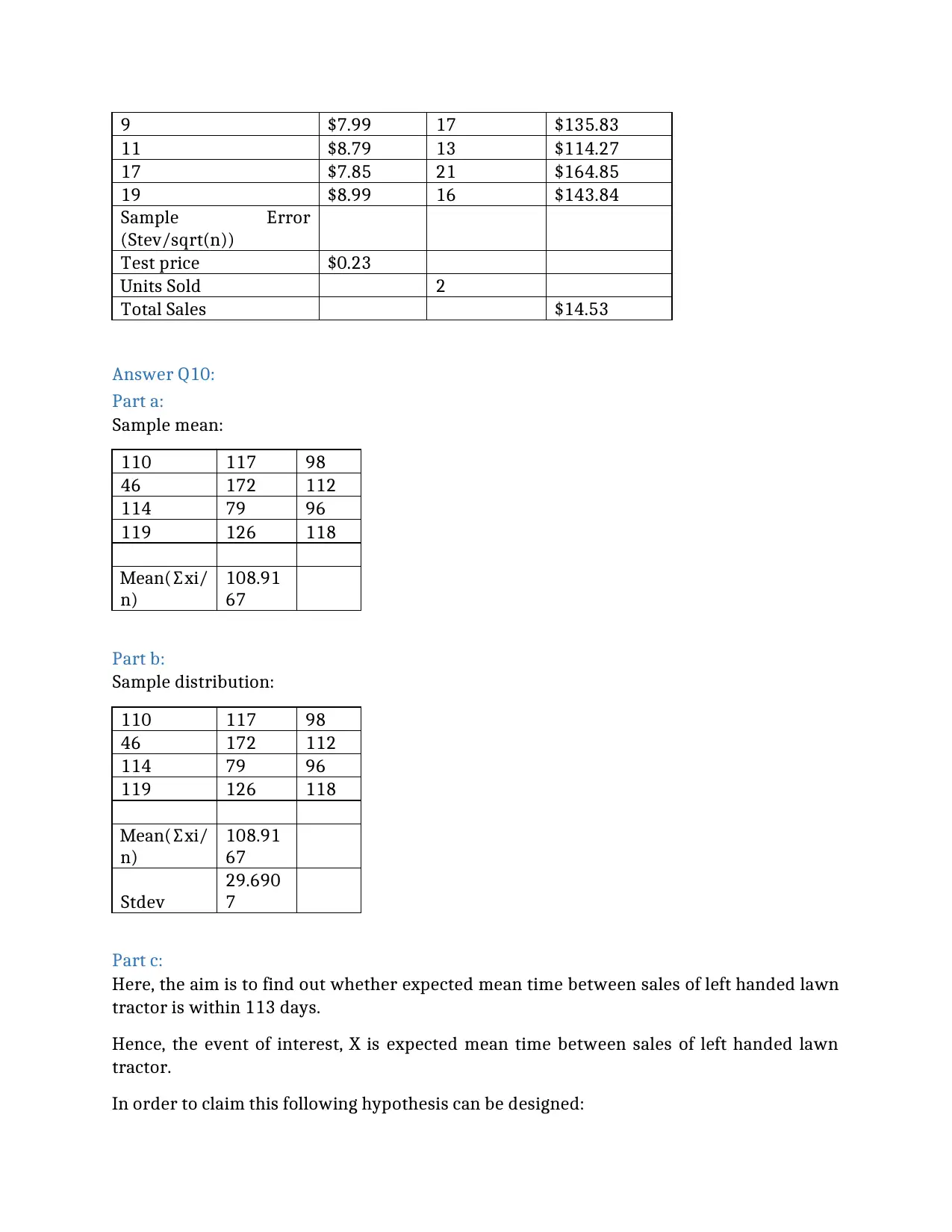
9 $7.99 17 $135.83
11 $8.79 13 $114.27
17 $7.85 21 $164.85
19 $8.99 16 $143.84
Sample Error
(Stev/sqrt(n))
Test price $0.23
Units Sold 2
Total Sales $14.53
Answer Q10:
Part a:
Sample mean:
110 117 98
46 172 112
114 79 96
119 126 118
Mean(∑xi/
n)
108.91
67
Part b:
Sample distribution:
110 117 98
46 172 112
114 79 96
119 126 118
Mean(∑xi/
n)
108.91
67
Stdev
29.690
7
Part c:
Here, the aim is to find out whether expected mean time between sales of left handed lawn
tractor is within 113 days.
Hence, the event of interest, X is expected mean time between sales of left handed lawn
tractor.
In order to claim this following hypothesis can be designed:
11 $8.79 13 $114.27
17 $7.85 21 $164.85
19 $8.99 16 $143.84
Sample Error
(Stev/sqrt(n))
Test price $0.23
Units Sold 2
Total Sales $14.53
Answer Q10:
Part a:
Sample mean:
110 117 98
46 172 112
114 79 96
119 126 118
Mean(∑xi/
n)
108.91
67
Part b:
Sample distribution:
110 117 98
46 172 112
114 79 96
119 126 118
Mean(∑xi/
n)
108.91
67
Stdev
29.690
7
Part c:
Here, the aim is to find out whether expected mean time between sales of left handed lawn
tractor is within 113 days.
Hence, the event of interest, X is expected mean time between sales of left handed lawn
tractor.
In order to claim this following hypothesis can be designed:
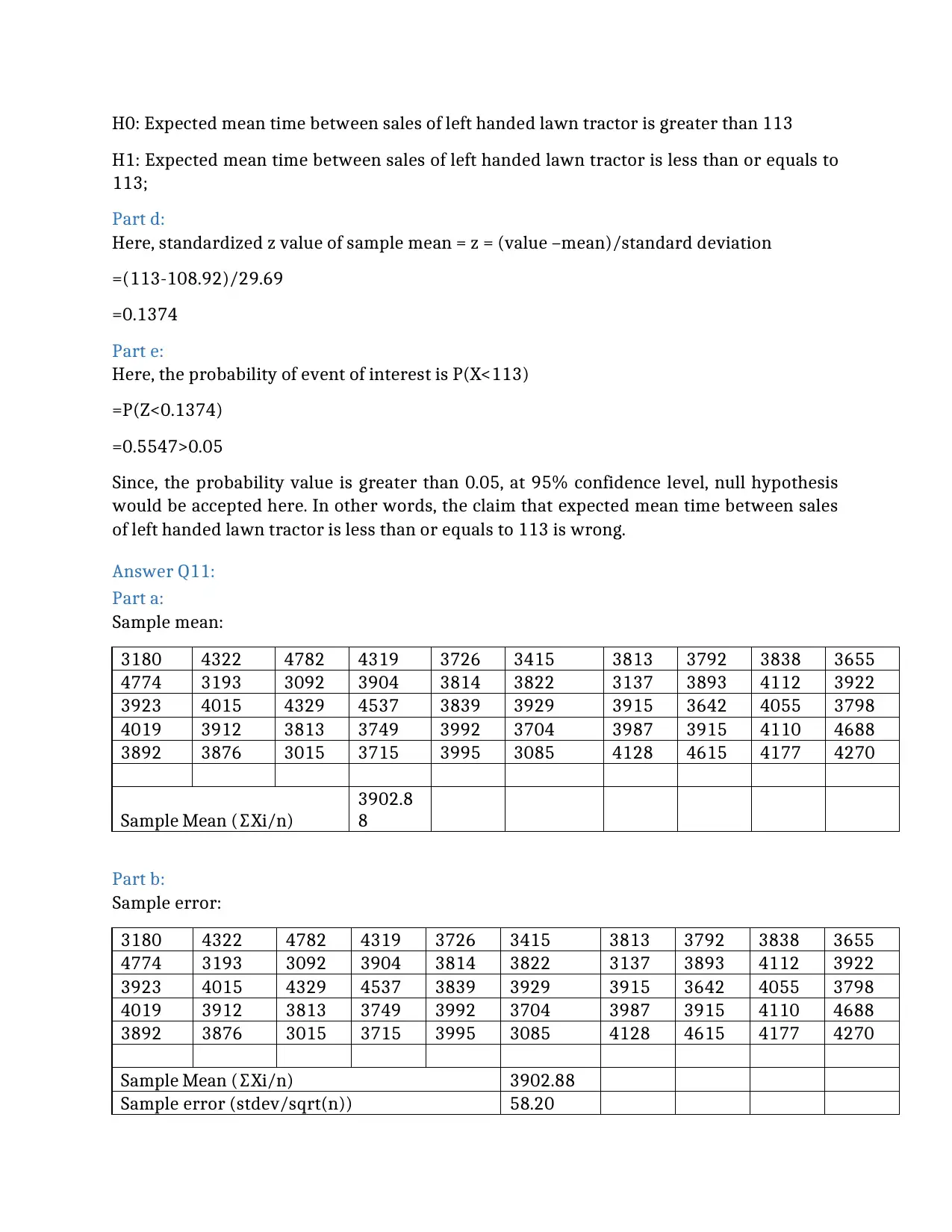
H0: Expected mean time between sales of left handed lawn tractor is greater than 113
H1: Expected mean time between sales of left handed lawn tractor is less than or equals to
113;
Part d:
Here, standardized z value of sample mean = z = (value –mean)/standard deviation
=(113-108.92)/29.69
=0.1374
Part e:
Here, the probability of event of interest is P(X<113)
=P(Z<0.1374)
=0.5547>0.05
Since, the probability value is greater than 0.05, at 95% confidence level, null hypothesis
would be accepted here. In other words, the claim that expected mean time between sales
of left handed lawn tractor is less than or equals to 113 is wrong.
Answer Q11:
Part a:
Sample mean:
3180 4322 4782 4319 3726 3415 3813 3792 3838 3655
4774 3193 3092 3904 3814 3822 3137 3893 4112 3922
3923 4015 4329 4537 3839 3929 3915 3642 4055 3798
4019 3912 3813 3749 3992 3704 3987 3915 4110 4688
3892 3876 3015 3715 3995 3085 4128 4615 4177 4270
Sample Mean (∑Xi/n)
3902.8
8
Part b:
Sample error:
3180 4322 4782 4319 3726 3415 3813 3792 3838 3655
4774 3193 3092 3904 3814 3822 3137 3893 4112 3922
3923 4015 4329 4537 3839 3929 3915 3642 4055 3798
4019 3912 3813 3749 3992 3704 3987 3915 4110 4688
3892 3876 3015 3715 3995 3085 4128 4615 4177 4270
Sample Mean (∑Xi/n) 3902.88
Sample error (stdev/sqrt(n)) 58.20
H1: Expected mean time between sales of left handed lawn tractor is less than or equals to
113;
Part d:
Here, standardized z value of sample mean = z = (value –mean)/standard deviation
=(113-108.92)/29.69
=0.1374
Part e:
Here, the probability of event of interest is P(X<113)
=P(Z<0.1374)
=0.5547>0.05
Since, the probability value is greater than 0.05, at 95% confidence level, null hypothesis
would be accepted here. In other words, the claim that expected mean time between sales
of left handed lawn tractor is less than or equals to 113 is wrong.
Answer Q11:
Part a:
Sample mean:
3180 4322 4782 4319 3726 3415 3813 3792 3838 3655
4774 3193 3092 3904 3814 3822 3137 3893 4112 3922
3923 4015 4329 4537 3839 3929 3915 3642 4055 3798
4019 3912 3813 3749 3992 3704 3987 3915 4110 4688
3892 3876 3015 3715 3995 3085 4128 4615 4177 4270
Sample Mean (∑Xi/n)
3902.8
8
Part b:
Sample error:
3180 4322 4782 4319 3726 3415 3813 3792 3838 3655
4774 3193 3092 3904 3814 3822 3137 3893 4112 3922
3923 4015 4329 4537 3839 3929 3915 3642 4055 3798
4019 3912 3813 3749 3992 3704 3987 3915 4110 4688
3892 3876 3015 3715 3995 3085 4128 4615 4177 4270
Sample Mean (∑Xi/n) 3902.88
Sample error (stdev/sqrt(n)) 58.20
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Part c:
Here, the event of interest X is mean monthly rental.
In order to claim this following hypothesis can be designed:
H0: Mean monthly rental is equals to 3987
H1: Mean monthly renal is not equals to 3987;
Part d:
Here, the sampling distribution is mean = 3902.88 and standard deviation = 58.20
Part e:
Here, the probability of interest is P(z = (3987-3902)/5820)
= P(z = 0.0146)
=0.5058>0.05
Since, the probability value is greater than 0.05 at 95% confidence level, it ca be concluded
that null hypothesis would be accepted here. In other words the mean monthly rental is
3987.
Answer Q12:
Part a:
Population proportion: here, total production is 25000 and out of which 15000 is finished
in pewter.
Hence, the population proportion = 15000/25000 = 0.6
Part b:
Sample proportion: here, a sample of 50 signs was taken into consideration out of which 37
were finished in pewter.
Hence, the sample proportion = 37/50 = 0.74
Part c:
Sampling error = Standard deviation of sampling distribution = sqrt(p*(1-p)/n)
= sqrt(0.74*(1-0.74)/50)
=0.0620
Here, the event of interest X is mean monthly rental.
In order to claim this following hypothesis can be designed:
H0: Mean monthly rental is equals to 3987
H1: Mean monthly renal is not equals to 3987;
Part d:
Here, the sampling distribution is mean = 3902.88 and standard deviation = 58.20
Part e:
Here, the probability of interest is P(z = (3987-3902)/5820)
= P(z = 0.0146)
=0.5058>0.05
Since, the probability value is greater than 0.05 at 95% confidence level, it ca be concluded
that null hypothesis would be accepted here. In other words the mean monthly rental is
3987.
Answer Q12:
Part a:
Population proportion: here, total production is 25000 and out of which 15000 is finished
in pewter.
Hence, the population proportion = 15000/25000 = 0.6
Part b:
Sample proportion: here, a sample of 50 signs was taken into consideration out of which 37
were finished in pewter.
Hence, the sample proportion = 37/50 = 0.74
Part c:
Sampling error = Standard deviation of sampling distribution = sqrt(p*(1-p)/n)
= sqrt(0.74*(1-0.74)/50)
=0.0620
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.