BUSN7051 Assignment 1 - Formulation and Solution of Linear Programs
VerifiedAdded on 2023/04/08
|6
|648
|421
Homework Assignment
AI Summary
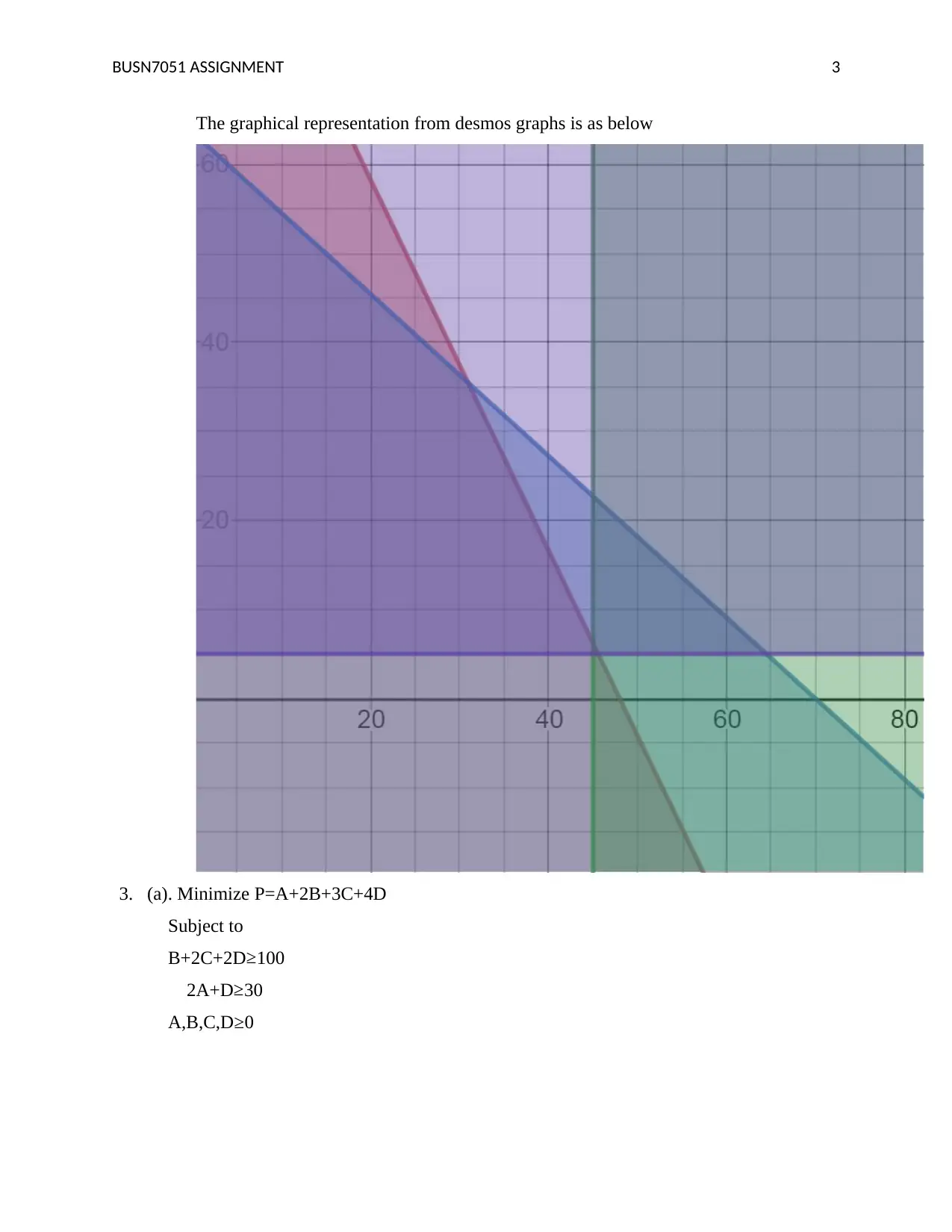
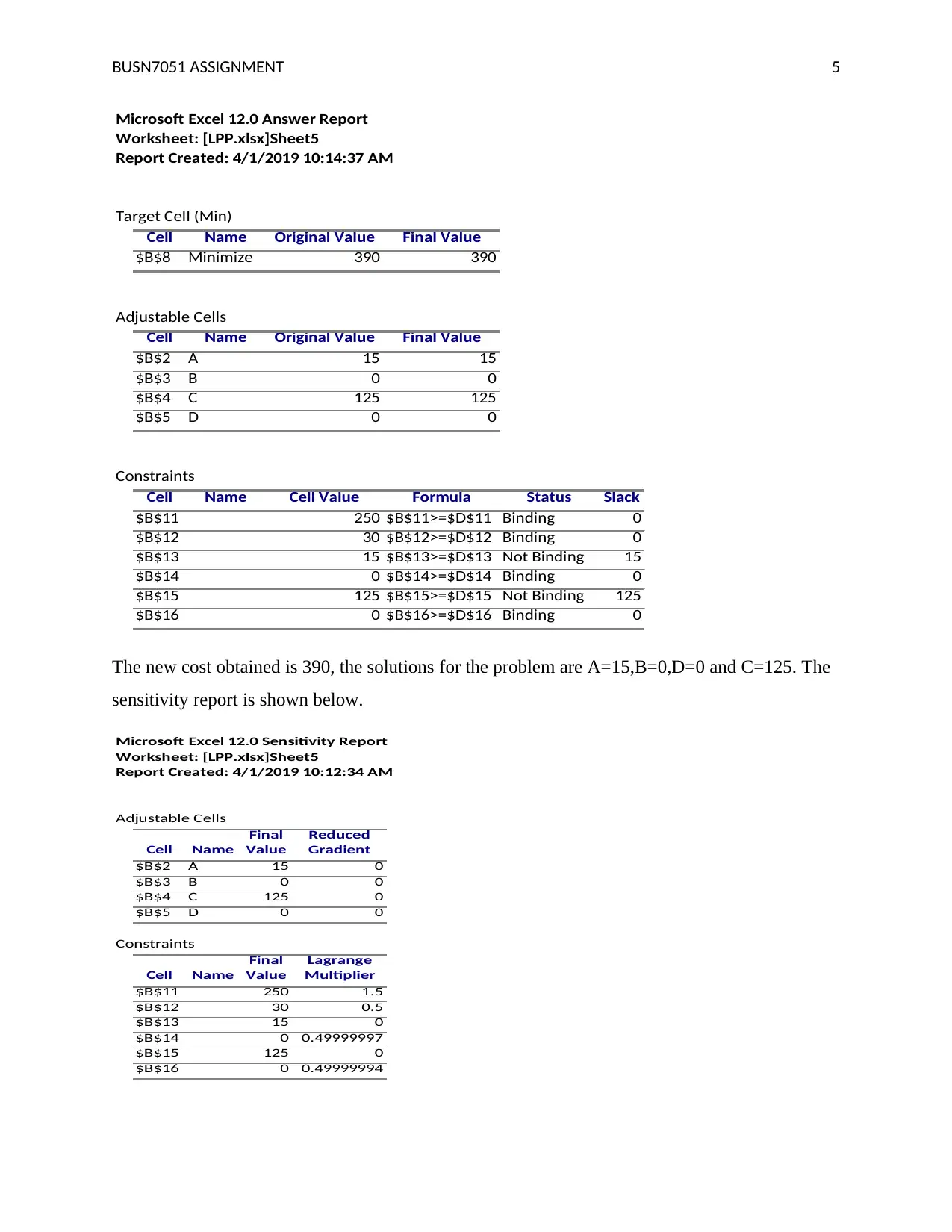
This document presents a comprehensive solution to BUSN7051 Assignment 1, focusing on linear programming techniques. The solution includes the formulation of a linear programming problem, determining variables, and defining the objective function to maximize production output. It outlines constraints related to machine processing times, initial stock levels, and demand forecasts for two products, X and Y. The solution utilizes the Iso-profit line method to find the optimal solution, followed by a graphical representation. The document further addresses a second linear programming problem, including minimizing costs and sensitivity analysis using Microsoft Excel. It provides the optimal solution, the minimum cost, and sensitivity reports, as well as a discussion of the impact of changing constraint values. The assignment concludes with a list of references, including key texts on operations management.
1 out of 6










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)