Statistics Homework: Calculations, Graphs, and Probability Analysis

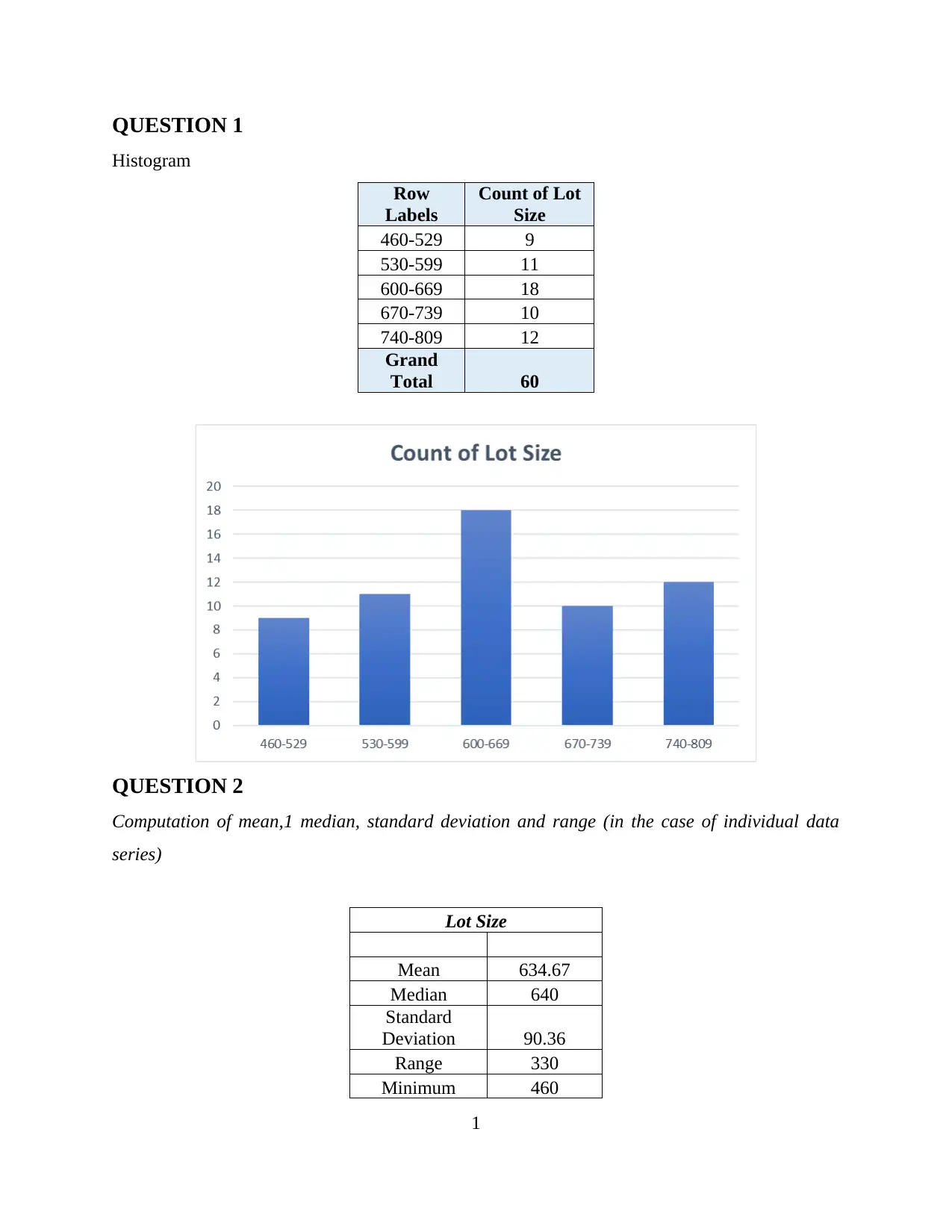
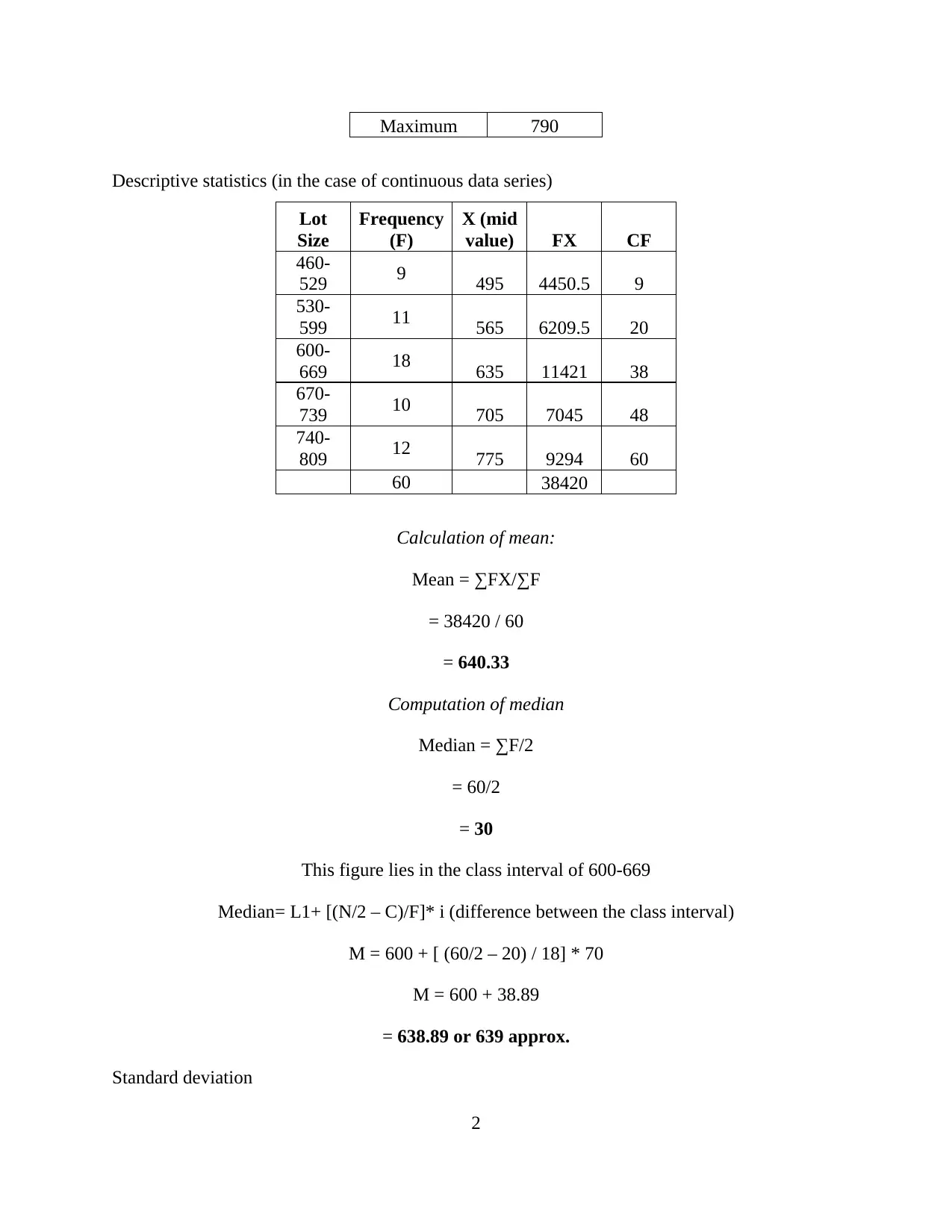
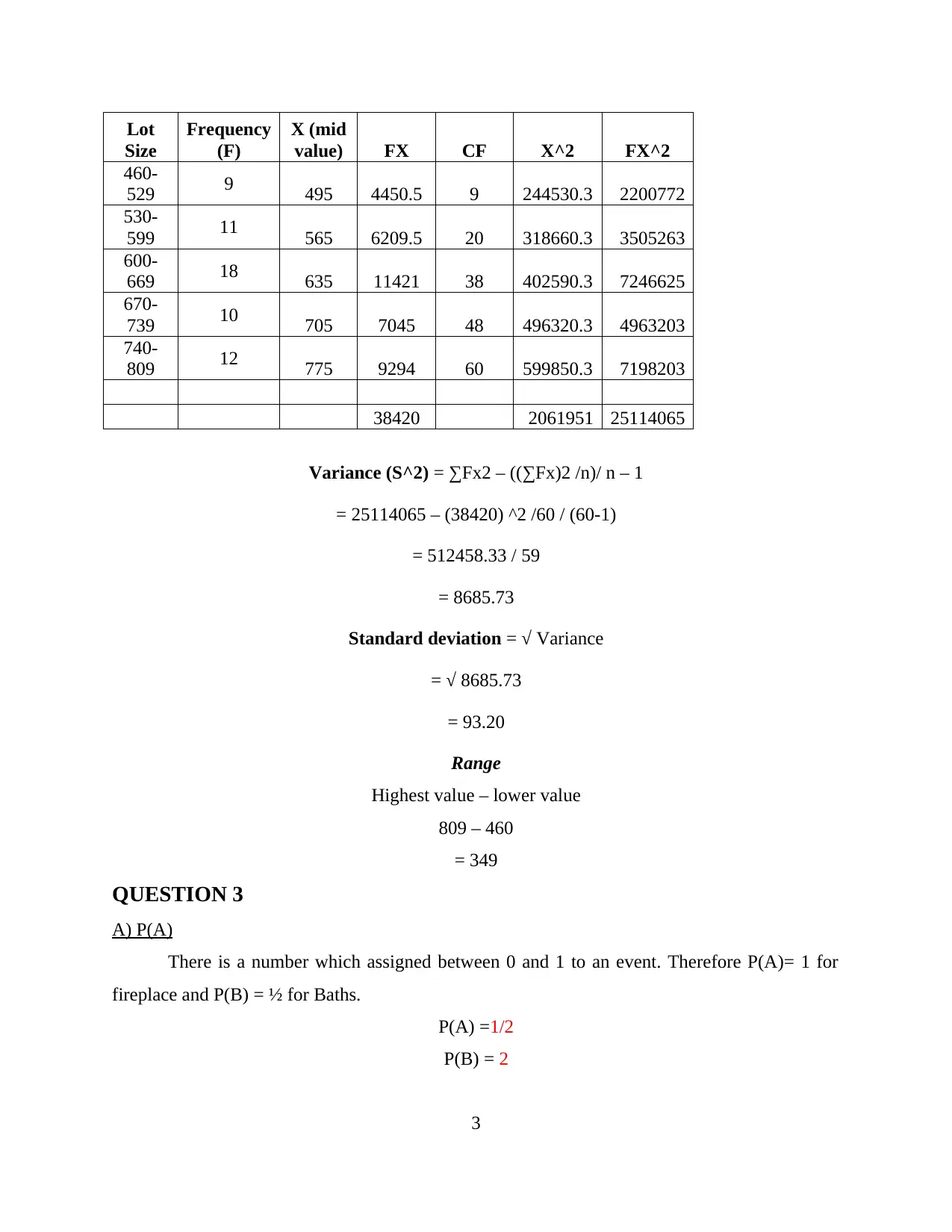
This statistics assignment solution encompasses a comprehensive analysis of data, including the construction of a histogram to visualize the distribution of lot sizes. The solution then proceeds to calculate key descriptive statistics such as mean, median, standard deviation, and range, both for individual and continuous data series, providing detailed formulas and step-by-step computations. Probability concepts are explored, with calculations for P(A), P(A ǀ B), and the conditions for independent events A and B. Finally, the assignment addresses the probability of a randomly selected property's value and the probability of sales falling below a certain threshold, applying statistical formulas to real-world scenarios.

Calculations and Statistical Graphs

TABLE OF CONTENTS
QUESTION 1...................................................................................................................................1
QUESTION 2...................................................................................................................................1
QUESTION 3...................................................................................................................................3
A) P(A)...................................................................................................................................3
B) P(A ǀ B)..............................................................................................................................4
C) Events for A and B for independent..................................................................................4
QUESTION 4...................................................................................................................................4
A) Value of randomly selected property is of $1 million.......................................................4
B) Probability of having sales less than $2 million................................................................4

QUESTION 1
Histogram
Row
Labels
Count of Lot
Size
460-529 9
530-599 11
600-669 18
670-739 10
740-809 12
Grand
Total 60
QUESTION 2
Computation of mean,1 median, standard deviation and range (in the case of individual data
series)
Lot Size
Mean 634.67
Median 640
Standard
Deviation 90.36
Range 330
Minimum 460
1

Maximum 790
Descriptive statistics (in the case of continuous data series)
Lot
Size
Frequency
(F)
X (mid
value) FX CF
460-
529 9 495 4450.5 9
530-
599 11 565 6209.5 20
600-
669 18 635 11421 38
670-
739 10 705 7045 48
740-
809 12 775 9294 60
60 38420
Calculation of mean:
Mean = ∑FX/∑F
= 38420 / 60
= 640.33
Computation of median
Median = ∑F/2
= 60/2
= 30
This figure lies in the class interval of 600-669
Median= L1+ [(N/2 – C)/F]* i (difference between the class interval)
M = 600 + [ (60/2 – 20) / 18] * 70
M = 600 + 38.89
= 638.89 or 639 approx.
Standard deviation
2

Lot
Size
Frequency
(F)
X (mid
value) FX CF X^2 FX^2
460-
529 9 495 4450.5 9 244530.3 2200772
530-
599 11 565 6209.5 20 318660.3 3505263
600-
669 18 635 11421 38 402590.3 7246625
670-
739 10 705 7045 48 496320.3 4963203
740-
809 12 775 9294 60 599850.3 7198203
38420 2061951 25114065
Variance (S^2) = ∑Fx2 – ((∑Fx)2 /n)/ n – 1
= 25114065 – (38420) ^2 /60 / (60-1)
= 512458.33 / 59
= 8685.73
Standard deviation = √ Variance
= √ 8685.73
= 93.20
Range
Highest value – lower value
809 – 460
= 349
QUESTION 3
A) P(A)
There is a number which assigned between 0 and 1 to an event. Therefore P(A)= 1 for
fireplace and P(B) = ½ for Baths.
P(A) =1/2
P(B) = 2
3

B) P(A ǀ B)
P(A ǀ B) = P(A . B)/P(B)
P(A ǀ B) = P( 1*1)/P(2)
P(A ǀ B) = ½ =0.5
C) Events for A and B for independent
P (A ǀ B) has denoted both variables as independent where event A occurred which does
not affect any changes in probability of B. Thus, as per considering the probability of having 2
bathrooms and a fireplace which insist that there will be no relation on each other for dependent
conditions. However, there have been two equivalent ways such as:
P (B ǀ A) = P(B)
P (A and B) = P (B ∩ A) = P(B) * P(A)
QUESTION 4
A) Value of randomly selected property is of $1 million
To analyses the probability of a randomly selected property can be analysed as
= X- μ/ 𝞼
= $650000- $1000000/ $S150000
= -2.33 or -2*1/3
However, as per the negative outcomes the probability of property to be valued is -2.33
or -2*1/3
B) Probability of having sales less than $2 million
= X- μ/ 𝞼/ √n
= $650000- $2000000/ $150000- √2000000
= -9
4