Use of Calculators in Mathematics Class: Impact on Students - Research Paper

This research paper analyzes the impact of calculators on students in mathematics class. It discusses the benefits and drawbacks of using calculators and provides statistical analysis of the results. The study was conducted on 50 sample students from a middle school in Temple, Texas. The findings indicate a positive effect of calculators on students' problem-solving skills and understanding of mathematical concepts.

Running head: RESEARCH PAPER
Use of Calculators in Mathematics Class
Name of the Student:
Name of the University:
Author’s Note:

1RESEARCH PAPER
Abstract
The fundamental objective of this research is to assess the usefulness of usage of calculators
in mathematics class among students. Various factors were identified, and statistical analysis
was conducted to observe the positive and negative effects of calculators and similar
strategies were explored to eliminate the drawbacks of using calculators. The study was
executed through two tests taken by the selected 50 sample students from a middle school in
Temple, Texas. The students could have access to a calculator only in the second test. The
findings indicated a positive effect of calculators as per the separately addressed research
questions. Initially, the prime focus of the research along with relevant background
information and significance of the study has been presented in the Introduction chapter.
Various articles, journals, and theories have been discussed in the literature review section to
provide a thorough understanding of the subject matter. Relevant methodologies and schemes
used and applied in this study have been discussed in detail in the Research Methods chapter.
Furthermore, interpretations of the outcomes in the form of statistical tables and graphs are
presented in the “Results” chapter of this study. The outcome of this investigation is believed
to assist the teachers understand and overcome adversities of the students.

2RESEARCH PAPER
Table of Contents
Chapter 1: Introduction and Literature Review.........................................................................4
1.1. Introduction.....................................................................................................................4
1.1.1. Statement of the Problem.........................................................................................4
1.1.2. Background Information..........................................................................................5
1.1.3. Significance of the Study.........................................................................................6
1.2. Literature Review............................................................................................................6
1.2.1. Benefits to using calculators in class.......................................................................8
Handheld Graphing Technology........................................................................................9
1.2.2. Drawbacks of using calculators in class.................................................................10
1.2.3. Definition of Terms................................................................................................11
1.2.4. Research Questions................................................................................................12
Chapter Two: Methods and Procedures...................................................................................12
2.1. Research Design............................................................................................................12
2.2. Setting and Participants.................................................................................................13
2.3. Instruments and Techniques used to collect data..........................................................14
2.4 Instructional Techniques used before Data Collection..................................................15
2.5 Data Collection Procedures............................................................................................15
2.6 Data Analysis Procedures..............................................................................................15
Chapter Three: Results.............................................................................................................16

3RESEARCH PAPER
3.1 Representation and explanations of the findings of Data Analysis................................16
3.2. Hypotheses:...................................................................................................................17
3.3. Graphs and Diagrams:...................................................................................................18
Chapter Four: Discussion.........................................................................................................23
Chapter Five: Conclusion and Recommendation.....................................................................25
5.1. Conclusion.....................................................................................................................25
5.2. Recommendation:.........................................................................................................25
References:...............................................................................................................................27
Appendix:.................................................................................................................................31
Survey Questionnaires:........................................................................................................33

4RESEARCH PAPER
Table of Figures
1. Bar chart of frequency distribution of time to finish the tests…………………….20
2. Bar chart of frequency distribution of word count of answer sheets ……………..21
3. Bar chart of frequency distribution of number of errors…………………………..21
4. Bar chart of frequency distribution of overall scores received by the students……22
5. Bar chart of frequency distribution of difficulty levels of calculation…………….22

5RESEARCH PAPER
List of Tables
1. t-Test table for H0A……………………………………………………………………………………………23
2. t-Test table for H0B……………………………………………………………………………………………23
3. t-Test table for H0C……………………………………………………………………………………………23
4. t-Test table for H0D……………………………………………………………………………………………24
5. Data acquired from the two tests………………………………………………32
6. t-Test tables for easy difficulty level…………………………………………..36
7. t-Test tables for hard difficulty level…………………………………………..37
8. t-Test tables for moderate difficulty level……………………………………..39
6.

6RESEARCH PAPER
Chapter 1: Introduction and Literature Review
1.1. Introduction
We live in an age of modern technology. Hence, we are memorizing multiplication facts
or working calculation out as pencil and paper has become out of date and waste of time.
Students learning of mathematical processes, concepts, operations and procedures are
advanced as calculators are used for an instructive purpose that goes beyond drill, practice or
checking work (Susskind, 2005).
Calculators have become an integral part of any student’s life. The students are given the
permission to access calculators only after the 7th grade. As majority of the tests taken have
the form of multiple choice answering system, calculators are becoming less redundant as the
closest answer to the calculations can be chosen as the answer. However, event test takers
have taken a note of that and the options provided have close to each other. Calculators are a
unique piece of technology, that when used appropriately can help in the calculations majorly
(Etlinger, 1974). With the increasing tendency to use the calculators even when not needed, it
has become a concern for the teachers as well parents.
It cannot be denied that using calculators save a lot of time that can be instead spent
focusing on comprehending and producing a detailed solution (Koay, 2006). Besides,
strategic utilization of calculators in the elementary grade students mathematically makes
necessary connections across mathematical ideas and methods in real-life circumstances
(Ellington, 2003).
1.1.1. Statement of the Problem
This research investigates the issue of the usage of calculators in mathematics class by
students and its impact. The statement of the problem is stated as – Use of calculator today

7RESEARCH PAPER
permits students and teachers to expend more time increasing mathematical perception,
reasoning, sense of number and its applicability by decreasing time that was used to spend on
learning and performing monotonous paper and pencil work based on arithmetic operations
and algebraic algorithm in the past. The statement of the research is established in accordance
to the Act USI/CPMSA, 1997.
1.1.2. Background Information
According to Suydam (1987), more than 100 studies conducted on this topic show
that using calculators helps get work done faster with much greater accuracy. Using
calculators also help increase the understanding of the subject matter as more time could be
spent on comprehension of the subject (National Council of Teachers of Mathematics, 2008).
However, over usage of calculator can reduce the ability to solve basic and easy sums.
Students who use calculators on a usual foundation tend to be habituated with it and in the
absence of calculators fail to solve relatively easier sums. Also, without appropriate
knowledge of the theories of the subject, students tend to indulge in problems that include
heavy calculations. It is necessary to have a thorough knowledge of the subject before
quantitative analysis is carried out. The inherent mathematical concepts or theories are often
missed out when using calculators to find the ultimate value.
Ultimately, all these give students a false impression of their ability to solve
mathematical sums and provide a false sense of confidence in them. It is obvious that every
piece of technology can be utilized in a good and bad way. It is up to the user either to use it
for enhancing the quality of output or just to minimize efforts. On the other hand, using
calculators take away many unnecessary efforts that could be tedious and boring (Deochand,
Costello and Fuqua, 2015). Without any such hindrance, students can focus more on the
conceptual part of the problem that in turn would help the student have better understanding
of the subject matter. However, with such progress in technology and in calculators, scientific

8RESEARCH PAPER
calculators provide a lot that could help students even cheat in exams. Formulas and values
can be stored in the calculators which help cheat in exams. Thus, a proper policy regarding
the usage of calculators by students should be implemented in the schools. This would help
restrict the usage up to a certain level.
The level of achievement, problem-solving skills and understanding of mathematical
ideas mainly improve with the help of use of calculators in 8th grade and afterwards.
1.1.3. Significance of the Study
This research signifies the usage of calculators by students in school and its
corresponding impacts. Various prospects of positive and negative impacts on students have
been discussed and analysed, which could help construct a guideline to restrict any such.
With enhancement in the field of technology, students should be well aware of and
acquainted with such. This study helps understand the need of the theoretical basis and the
process of calculators makes it easy to have a better understanding of the subject.
Mathematics is always being a vibrant subject among the learners. The task of
calculation becomes easy with the help of calculators. It might decrease the underlying
mathematical calculations and ideas; but must inhibit students from observing the inherent
patent in mathematical associations. The adoption of advanced technology in terms of
calculators would help to solve day-to-day as well as exam mathematics during a high scale.
1.2. Literature Review
Calculators influence the motives of educational engagement of a student both
positively and negatively. In the paper published by Wu et al., (2012) discusses the increase
in usage of mobile devices for the betterment of education. The authors portrayed their
objective as “The present study finds these factors represent the overall research trends and
patterns in the field”.

9RESEARCH PAPER
The vast debate over the use of calculator in mathematics classroom specifically in
elementary school would probably never be resolved. In case of calculative and problem-
solving skills, Hembree and Dessart (1986) alienated the studies dependent upon the method
of investing and analysed every group individually. As per their study, while calculators were
component of the assessment method, the calculative and problem-solving skills of students
enhanced.
The outcomes were cheering for the function of calculators in classroom study of
mathematics. Mainly two types of skills (1. Operational, computational and conceptual 2.
General problem-solving skills) are attempted as the outcome of having access to a calculator
at the time of direction and the capability to choose the proper strategy of problem-solving
(Chen and Lai, 2016). This analysis helps to reveal the role of calculator in the development
of attitude of students towards mathematics. According to the journals of Dye (1981), Lloyd
(1991) and Lawrance & Dorans (1994), the usage of calculator enhances the performance on
computational items. Besides, it looks that graphing calculators were more expected to be
linked with increment of scores and it had little influence on the speed with which student
accomplished the test.
Starting from the initial phase learning to the high school, calculators are erasing the
inclemency regarding big multiplication or division (Milou, 1999). From the previous exam,
teachers felt that calculator has helped students to perform subsequent tests on multiplicative
factors. According to Pearson (2010), if the use of calculator is allowed, then examinees
should depend on their skills at the time of imputing arithmetic and geometric problems in
the calculator for answering the items properly.

10RESEARCH PAPER
1.2.1. Benefits to using calculators in class
With the growth of mathematics in past few decades, the availability of technological
tools to help the students has evolved rapidly as well. Mathematics has emerged to be a
subject of paramount importance (National Council of Teachers of Mathematics, 2014). It is
vital for the students to cultivate a thorough and proper understanding of the subject and to
develop a logical assessment temperament (Ansley, Spratt and Forsyth, 1989). Introduction
of scientific calculators and hand-held graphing calculators contribute to the progress in the
subject field over all. These are considered useful and powerful mathematical tools that
enable students to conduct an in-depth analysis on the topic at hand. Using calculators also
decrease the time to solve any sum to a great length. Rohrabaugh & Cooper (2016) presented
the following benefits of using calculators in their study. Suydam (1985) stated that when
students use graphical calculators, they are being more involved in problem solving
techniques that enlarge their achievement.
In the statement of Colton and Gao (1997), outcomes of the research were unstable
concerning the ability to the student with a couple of studies proposing a discrepant
usefulness favouring the students of lesser capability.
According to the authors,
● Calculator helps save time for the students/educator because it gets rid of tedious
steps in certain problems, such as three-digit multiplication.
● Usage of calculator brings an engaging aspect into mathematics classrooms.
● If the answers of both students do not line up, students can go back and re-check
their work to observe where they may have gone wrong (Bridgeman, Harvey and Braswell,
1995).

11RESEARCH PAPER
● Calculators are valuable for validating work. Students should learn the use of
calculators that is a helpful tool delivering help and fast answers.
● Calculators help to explore and discover the elementary operation of the
classroom (Rakes et al., 2011).
● Instead of long and tedious calculation by hand, students could see the patterns
quickly with a calculator.
● Additionally, students focus on the concept and new ideas of computation by
calculators (Kutzler, 2000).
● Helpful and effective use of calculators can easily avoid careless mistakes.
● Basic computations by calculators provide a good understanding of estimation.
● Mathematics could be tough, but, calculators might make it enjoyable.
According to Dunham and Dick (1994), technology in terms of calculators can
motivate students to learn mathematics. It is a known fact that use of calculators is
widespread, and technology improved classrooms is more prevalent.
Handheld Graphing Technology
Handheld graphing calculators were introduced in 1990’s and have been in practice
since. Teaching methods were modified to incorporate the usage of these as it received
positive feedbacks (Math et al., 2018). The main objective behind invention of such a tool
was to enrich the student’s perceptive of the subject by confronting the problems with the
help of a visual representation. Although in general such calculators are used to solve
mathematical problems, it is also used in fields of engineering or statistics as well. Usually
students of higher grades tend to use the graphing calculators. It can even produce graphs of

12RESEARCH PAPER
mathematical functions. According to Rohrabaugh & Cooper (2016), “By having access to
these graphs, students can see different transformations of parent functions, find the
intercepts, asymptotes, and are even provided with a table”.
Hembree and Desart (1986) showed in their articles that along with traditional
instruments like pen and paper, support of calculator is enhancing the ability levels of the
students. A related study of Barton (2001) indicates that usage of calculators had
considerably higher accomplishment in mathematics and substantial deviation in the qualities
and attitudes of the students. A referential study of Waits and Demana (200) proposed an
approach of paper and pencil as well as calculators for the joint learning and teaching
methods of mathematics.
1.2.2. Drawbacks of using calculators in class
While calculators provide a wide range of benefits for mathematical calculations, it
does however have some barriers to its usage as well. Baker, Lusk & Neuhauser, (2012)
conducted a research on the use of electronic devices in classroom by surveying faculty and
students. It is mentioned in the study that over reliance on these technologies cannot
guarantee an improved learning, instead possesses the risk of distracting the student and
consequently lower the student’s engagement with the subject. It depends on the student and
teacher and even the classroom environment where as the student will develop a tendency to
overuse calculators (Andrews and Brown, 2015). The possibility of students becoming
familiar with calculators cannot be disregarded. From the student’s perspective, he or she
might think it is the easier or familiar method of solving problems and thus indulge in doing
so without realizing the possible consequences. Thus, strict policies regarding the use of
calculators should be implemented in schools and colleges to restrict the students from
develop an overreliance on calculators.

13RESEARCH PAPER
Some people consider that there should be no place for calculator in the classroom
especially in primary and high school (National Council of Teachers of Mathematics, 2015).
It may be needed only in case of post matriculation study. The main reason behind this
suggestion is that it could hamper the practice of “mental math” (Powell, 2015). Pupils might
receive an unreal realization about the lack of confidence about their ability in mathematics.
Students fail to show their interest in complicated mathematics as calculator had an actual
negative use. Calculators that can perform a variety of things put immense bad effect on the
habit of students. Therefore, a calculator policy can only justify at what limit of calculators
could be allowed to the students (Quesada, 1996). A general concern relating the use of
calculator on assessment of large scale permits the use of calculator of the scores that
examinees obtain.
1.2.3. Definition of Terms
Calculator math and non-calculator math are tough things to balance. Therefore, a
look at some terms, contexts and definitions with using calculator in the classroom and exam
is required.
Calculator: A calculator is an electronic device, which performs operations on numbers. The
simplest calculators allowed for students can do addition, subtraction, multiplication and
division.
Graphical Calculator: The calculator that has four-function, graphing techniques and other
complex scientific features like CAS is known as graphical calculator (Doerr and Zangor,
2000).
Mathematical Accuracy: Mathematical accuracy is a measure that increases when number
of errors decrease in mathematics. Calculators are fast and accurate that makes students many
complementary features for students (Simmt, 1997).

14RESEARCH PAPER
1.2.4. Research Questions
Based on the literature review presented in this study, the relevant issues that should
be explored are as follows -
1. What are the effects of using calculators on students during mathematical assessment tests?
2. Does the use of calculators help students understand the basic theoretical concepts that are
been taught in class better?
3. What is the appropriate timing and conditions to use calculators for maximum need
(Wheatley, 1980)?
4. Is it of utmost importance to keep a track of whether the students’ learning of core
mathematical skills is being hindered using calculators or is it actually being enhanced?
Chapter Two: Methods and Procedures
To present a research study that yields accurate and specific results, relevant
analytical tools and procedures must be utilized. Quantitative research with proper statistical
analysis ensures the authenticity of the study. In this chapter, the relevant methods and
procedures have been discussed.
2.1. Research Design
Research design is a blue print of the procedures that enable the research to test
hypothesis by reaching valid conclusions about the association between dependent and
independent variables. It is a structurally and strategically research design for obtaining
answer to research question for controlling variances. The scheme of paradigm is the
operation of variables. Research design is the overall operational pattern of the project that
stipulates information of procedures.

15RESEARCH PAPER
The three most popular types of conducting research are quantitative, qualitative and
mixed method. There has been a lot of debate regarding the appropriate and best
methodology; however, it depends on the requirements of the topic at hand. Various
researchers prefer various processes deepening on the respective research work. After careful
consideration of the three methodologies, the selected methodology for this study is that of
quantitative method. This research revolves around the impacts of using calculators in class.
Its primary focus is to comprehend the effect calculators have on students in math classes and
tests. The study is important to provide information about the impact of calculators. Three
different types of skills as well as obtained score is determined depending on the fact that
calculators were used or not. Outcome of scores helps to show the use of impacts to the total
score.
Detailed statistical analysis is executed to find the necessary explanations. Initially
after constructing the statistical hypotheses, relevant column graphs are also to be constructed
to have a basic understanding of the factors from both the tests. Two-sample t-Test assuming
unequal variances will be conducted to test the respective hypotheses. Two-similar tests will
be selected from the Texas Essential Knowledge and Skills website for the 7th and 8th grade
respectively.
2.2. Setting and Participants
The chosen school for this research is a middle school in Temple, Texas. According to
the report published in the ‘Public School Review Website’, sixth to eighth grade consists of
521 students in total. Among the selected population of students, 48% were Hispanic, 32%
were White, 17% were Black, 2% were Mixed Races and the rest 1% were Asians (Public
School Review, 2003-2016).

16RESEARCH PAPER
As the sample, the performance data of 50 students is chosen. Among these, 25
students will be from each “Regular math class” and “AP math class”. The students appeared
in two tests for consecutive weeks. Both the tests will have the same level of hardness and
would be presented unabashedly to the students. Students can use the calculator only in the
second test. The study is designed to include everyone and Individualized Educational Plan
(IEP) has been implemented for those who need it. Among the selected students, there are
four students with English as native language and two students who need Special Education.
Both the tests are taken on Friday, at the end of the week.
2.3. Instruments and Techniques used to collect data
Data has been collected based on the tests taken. With relevance to the mentioned
hypotheses, data for respective factors has been recorded for analysis. The time taken by the
students to finish the test has been recorded. The total word count in each solution papers is
also counted. Number of calculation errors made by the students while having and not having
access to a calculator is tabulated. Finally, after evaluation of the tests, scores are also
tabulated. Further, depending on the level of toughness in which each student has decided to
use the calculator has also been recorded as data. The tests will be of 20 minutes each and full
marks will be 20.
The data is gathered manually from recent activity. Therefore, the data is
experimental data. It is collected in a specific time point. Hence, the sampled data is cross
sectional data.
2.4 Instructional Techniques used before Data Collection
Before conducting the test, students became aware of the test and its procedures. The
tests were taken according to the school syllabus of the students. A brief introduction will be
provided to the students about the use the graphical calculators along with its relevant use.

17RESEARCH PAPER
Students are further encouraged to use the calculators to be acquainted, in case the student is
not fully aware of the functions of a calculator (Ruthven, 1990).
The instrumental techniques used before data collection is the personal investigation
taking prior permission from the beholder of the educational data. The confidentiality and
professionalism were maintained before data collection.
2.5 Data Collection Procedures
Procedure is the most crucial aspect in research methodology. Without proper
planning and procedure, researcher is unable to reach any conclusion. After choosing and
finalizing the tools for data collection, the researcher can begin the data collection procedure.
After gathering data from the sample, collected data was scored in the second cases.
The sample size is 50. The source of the data is also limited and authentic. Hence, the
data is collected by complete enumeration method. Complete enumeration process usually is
applied for intensive in-depth investigation, when the number of population is not large. The
method is expected to yield correct information. However, the huge non-sampling errors
influence outputs whose magnitudes cannot be determined. Complete enumeration refers a
complete count.
2.6 Data Analysis Procedures
The researcher is supposed to arrange the tests from the students to take and then
evaluate them. Help from teachers to evaluate the tests is permissible. From further analysis
of the data, it can be understood whether taking calculators help, hinder or just simply have
no effect on the various aspects of education of the students. If the scores of the test in which
students are permitted to access calculators, are higher than the other test, one could conclude
that using the help of calculator, the students score better. On the other hand, if the test scores

18RESEARCH PAPER
differ significantly, then it would imply that the basic concepts of the relevant subjects are not
being clearly retained by the students.
Statistical technique is applied to comprehend the data analysis methods. This
technique has classified and arranged the data and tried to explain the inherent patterns of the
dataset. Statistical technique is the utmost crucial method to solve a research problem. From
data collection to inference drawing, statistical procedures are systematically adopted.
Chapter Three: Results
3.1 Representation and explanations of the findings of Data Analysis
It is essential to state that students have utilised to a calculator only in the second test.
The data table refers the data for a variety of factors that have been tabulated to perform the
essential statistical hypothesis testing. To comprehend the impact of using calculators in
assessment tests, the following charts have been represented. The use of calculator in class is
beneficial for students that could dramatically change the scores of the tests. The researcher is
trying to find that fact.
Exploratory Data Analysis:
In the first test taken, students would not have right to use to a calculator. In the next
maths test, students are permitted to do so. The following hypotheses are structured in
congruence with the foresaid research questions. Exploratory data analysis is used in any
investigation to determine the testing. The collected data conducts the research. The analysis
of data relies upon the nature of the data. It adopts the systematic procedures to gather
necessary data. Relevant data, adequate inequality and quantity are gathered for exploratory
data analysis with sufficient validity and reliability.

19RESEARCH PAPER
3.2. Hypotheses:
First Hypotheses:
H0 A : The time taken¿ complete the test is more while usingcalculator .
H1 A :The timetaken ¿ complete thetest is while using calculator∧not using
calculator are same .
Second Hypotheses:
H0 B :The amount of theoretical description∈termsof word countis less while
using calculator .
H1 B :The amount of theoretical description various while using calculator .
Third Hypotheses:
H0 C : Higher number of calculational errors are made while usingcalculator .
H1 C : Less calculational errors are made while usingcalculator .
Fourth Hypotheses:
H0 D: The scores have not improved while using calculator .
H1 D : The scores have improved whileusing calculator .
For understanding the effects of using calculators while taking a test, the following
graphs are required to be investigated at the beginning.
From the graphs, it is evident that average time taken by the students in the first test,
without using calculators is 18.04 minutes. Whereas, in the second test, where students had

20RESEARCH PAPER
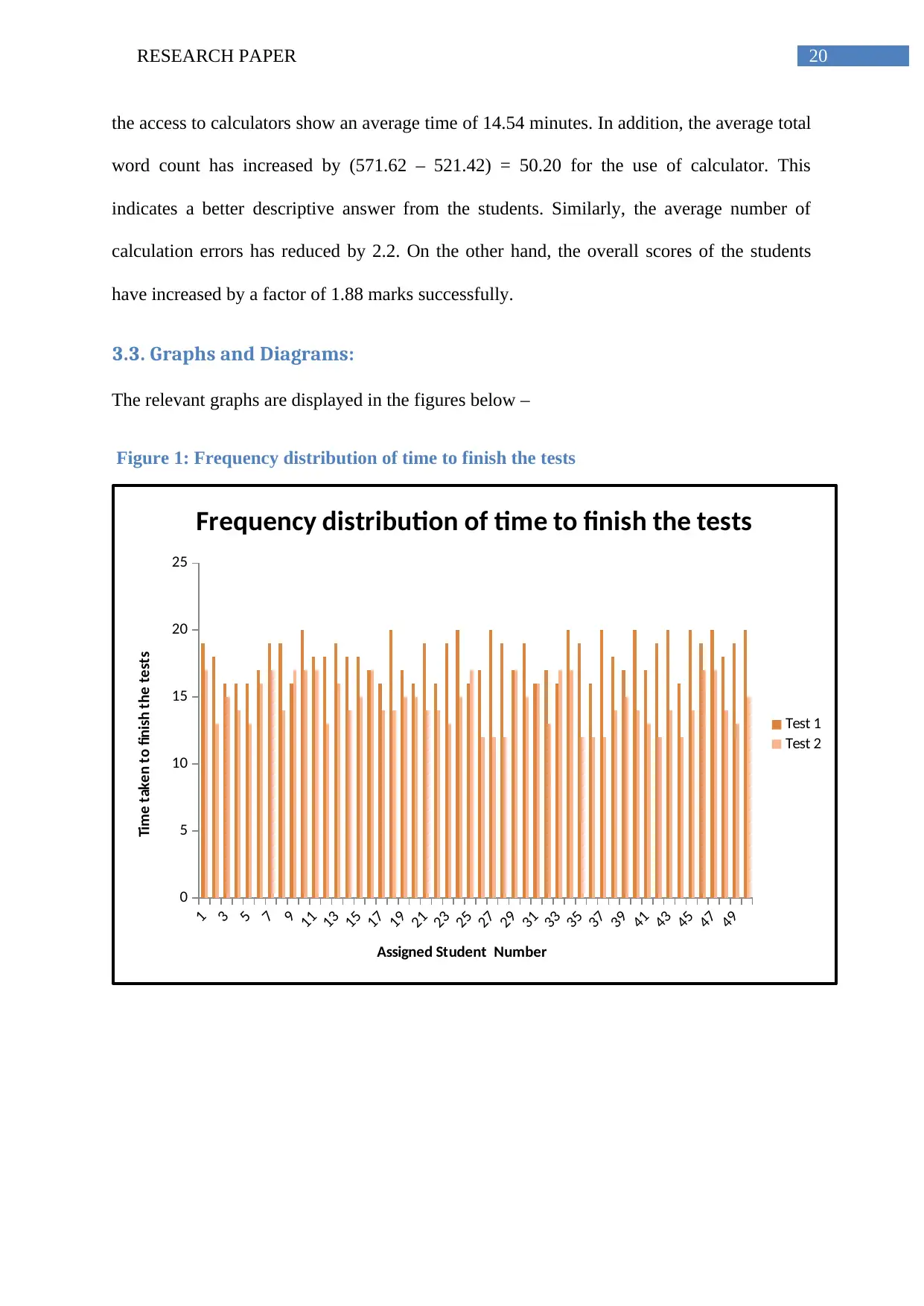
the access to calculators show an average time of 14.54 minutes. In addition, the average total
word count has increased by (571.62 – 521.42) = 50.20 for the use of calculator. This
indicates a better descriptive answer from the students. Similarly, the average number of
calculation errors has reduced by 2.2. On the other hand, the overall scores of the students
have increased by a factor of 1.88 marks successfully.
3.3. Graphs and Diagrams:
The relevant graphs are displayed in the figures below –
Figure 1: Frequency distribution of time to finish the tests
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
0
5
10
15
20
25
Frequency distribution of time to finish the tests
Test 1
Test 2
Assigned Student Number
Time taken to finish the tests

21RESEARCH PAPER
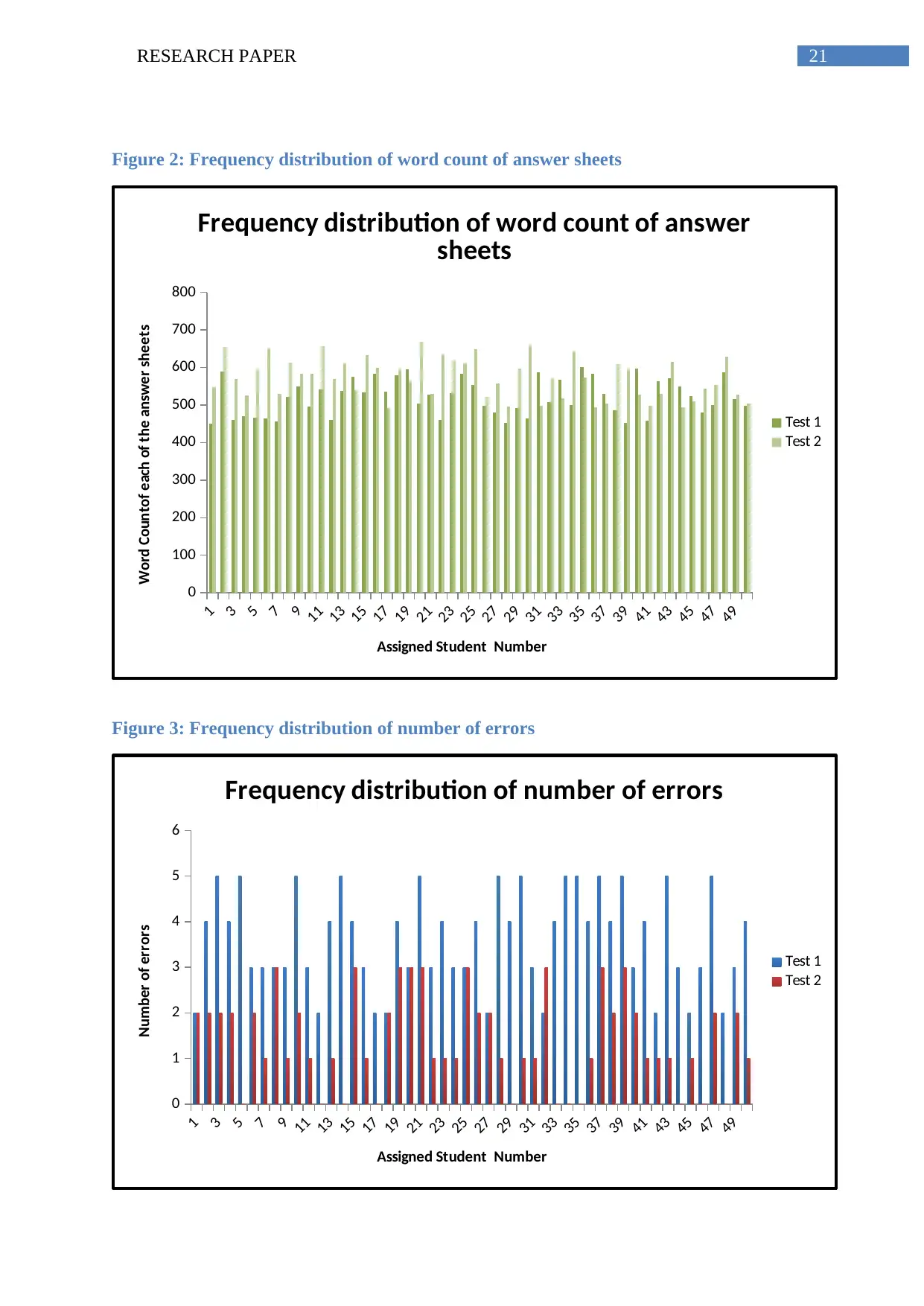
Figure 2: Frequency distribution of word count of answer sheets
1 3 5 7 91113151719212325272931333537394143454749
0
100
200
300
400
500
600
700
800
Frequency distribution of word count of answer
sheets
Test 1
Test 2
Assigned Student Number
Word Countof each of the answer sheets
Figure 3: Frequency distribution of number of errors
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
0
1
2
3
4
5
6
Frequency distribution of number of errors
Test 1
Test 2
Assigned Student Number
Number of errors

22RESEARCH PAPER
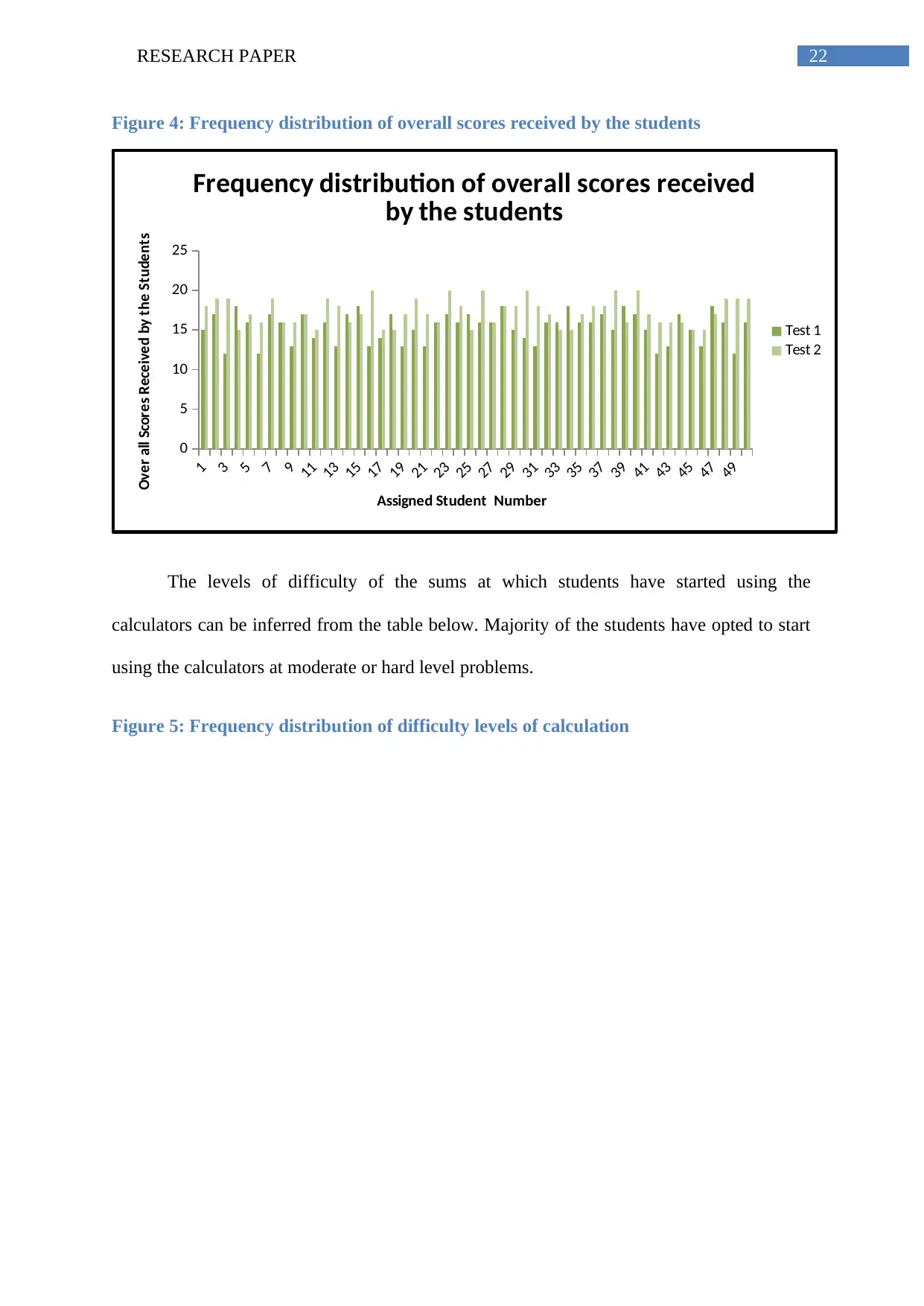
Figure 4: Frequency distribution of overall scores received by the students
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
0
5
10
15
20
25
Frequency distribution of overall scores received
by the students
Test 1
Test 2
Assigned Student Number
Over all Scores Received by the Students
The levels of difficulty of the sums at which students have started using the
calculators can be inferred from the table below. Majority of the students have opted to start
using the calculators at moderate or hard level problems.
Figure 5: Frequency distribution of difficulty levels of calculation

23RESEARCH PAPER
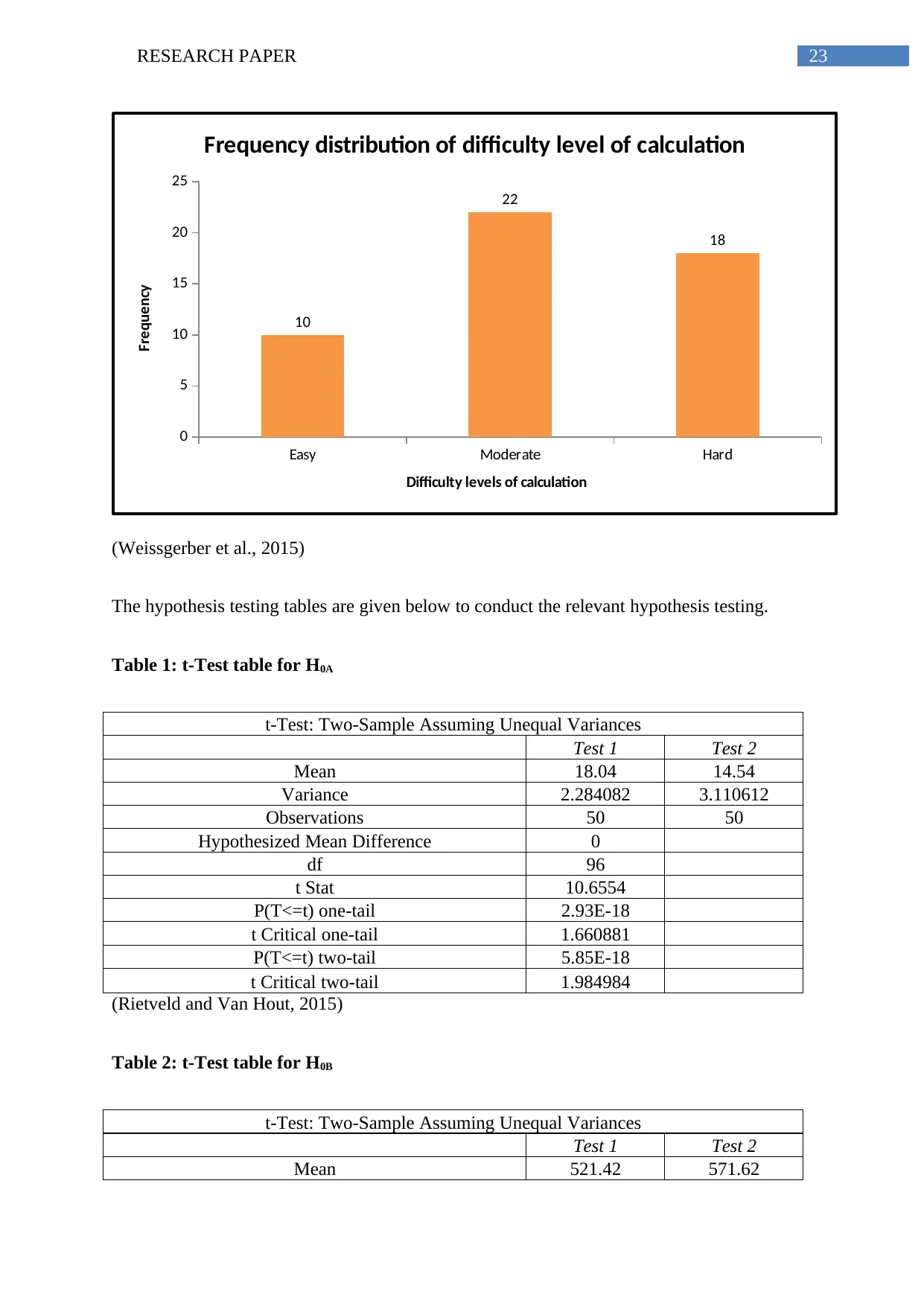
Easy Moderate Hard
0
5
10
15
20
25
10
22
18
Frequency distribution of difficulty level of calculation
Difficulty levels of calculation
Frequency
(Weissgerber et al., 2015)
The hypothesis testing tables are given below to conduct the relevant hypothesis testing.
Table 1: t-Test table for H0A
t-Test: Two-Sample Assuming Unequal Variances
Test 1 Test 2
Mean 18.04 14.54
Variance 2.284082 3.110612
Observations 50 50
Hypothesized Mean Difference 0
df 96
t Stat 10.6554
P(T<=t) one-tail 2.93E-18
t Critical one-tail 1.660881
P(T<=t) two-tail 5.85E-18
t Critical two-tail 1.984984
(Rietveld and Van Hout, 2015)
Table 2: t-Test table for H0B
t-Test: Two-Sample Assuming Unequal Variances
Test 1 Test 2
Mean 521.42 571.62

24RESEARCH PAPER
Variance 2313.269 2871.424
Observations 50 50
Hypothesized Mean Difference 0
df 97
t Stat -4.92978
P(T<=t) one-tail 1.7E-06
t Critical one-tail 1.660715
P(T<=t) two-tail 3.4E-06
t Critical two-tail 1.984723
Table 3: t-Test table for H0C
t-Test: Two-Sample Assuming Unequal Variances
Test 1 Test 2
Mean 3.6 1.4
Variance 1.142857 1.061224
Observations 50 50
Hypothesized Mean Difference 0
df 98
t Stat 10.47837
P(T<=t) one-tail 5.56E-18
t Critical one-tail 1.660551
P(T<=t) two-tail 1.11E-17
t Critical two-tail 1.984467
Table 4: t-Test table for H0D
t-Test: Two-Sample Assuming Unequal Variances
Test 1 Test 2
Mean 15.4 17.28
Variance 3.469387755 2.777143
Observations 50 50
Hypothesized Mean Difference 0
df 97
t Stat -5.318919471
P(T<=t) one-tail 3.34914E-07
t Critical one-tail 1.660714611
P(T<=t) two-tail 6.69827E-07
t Critical two-tail 1.984723136

25RESEARCH PAPER
The four two-sample t-tests referred that tier1 and tier2 have unequal averages at 95%
confidence interval for all the four variables that are “Time taken to finish the test”, “Word
country for theory”, “Number of calculation error” and “Scores”.
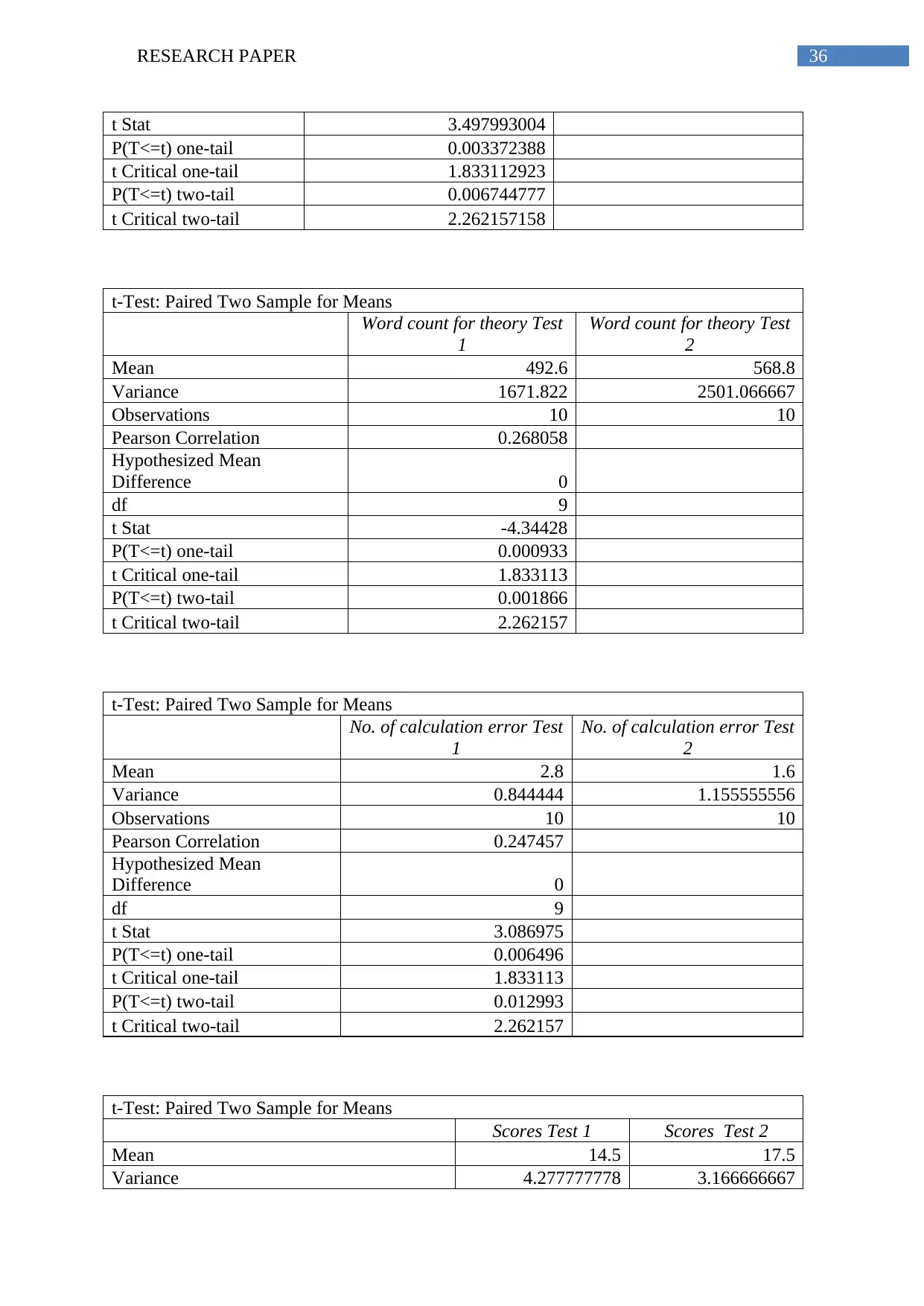
The two-sample t-tests of “Easy” difficulty level show that with the use of calculator
more word count, less number of calculation errors, less time consumption and more scores
are achieved. The two-sample t-tests of “Hard” difficulty level indicates that with the use of
calculator less time consumption, less number of calculation errors and more scores are
achieved. However, word count did not receive effective change due to use of calculators.
The two-sample t-tests of “Moderate” difficulty level refers that less time consumption, more
word count and less number of calculation errors are received as the advantage of calculator.
However, score of the exam has not changed due to use of calculators in moderate level of
difficulty.
Chapter Four: Discussion
Through respective statistical analysis, the constructed hypotheses were tested.
Graphs were also produced to provide a visual presentation of the scores for comparing the
scores between the two tests. From the detailed table report of the scores, it is evident that
usage of calculator helps the student score higher. From average values of the first two
columns, the average time taken by the students to finish the test decreased by 3.5 minutes.
This emphasizes the increment of word count. Students have more time to aim on writing the
descriptive part of the test. It would help student to have a thorough understanding of the
inherent mathematical theories and help them express at the time of tests. Calculation errors
are major drawbacks in mathematics assignments or tests. A simple miscalculation could
render the whole problem wrong. Thus, it is very important to solve the sums or calculate not
only faster, also correctly. Calculating with the help of calculator ensures the both time

26RESEARCH PAPER
saving and higher accuracy. It is evident from the data under study. There is a significant
drop of 2.2 errors for each student when they were permitted to use the calculator. On the
other hand, 1.88 marks have enhanced on an average for the students. This refers the
utilization of the calculators in a positive way.
Relevant statistical hypotheses testing actions were accomplished. The research
questions and respective statistical hypotheses have been declared before. Two-sample t-
Tests assuming unequal variances were executed to test the hypotheses. From table 1, the t
Statistics has been found out to be 10.665. Since p-value is less than the chosen level of
significance (0.05), the null hypothesis, H0A, has been rejected at 95% confidence interval.
Implying that the time needed to finish the test is less while using a calculator. From table 3,
same results could be drawn. The t-Stat value -4.9298. The p-value is also lower than the
level of significant value of 0.05. Thus, the null hypothesis, H0B, is rejected at 95%
confidence interval. This means students tend to provide better theoretical descriptions while
using calculator. Similarly, the null hypotheses, H0C and H0D have been rejected at 95%
confidence interval as both the p-values were less than 0.05. Thus, it could be concluded that
while the scores do improve while using a calculator, it also minimizes the calculation errors.
As mentioned before, if the scores of the two tests differed by a large scale, it would
have indicated inconsistency in the teaching methods as the students’ grades improved
significantly when they were given the opportunity to use the calculator. However, no such
indications could be observed from the data.

27RESEARCH PAPER
Chapter Five: Conclusion and Recommendation
5.1. Conclusion
The outcomes for attitudes of students and analogous independent variable analysis
help to draw inference in the result section. Duration of the test, broader summary analysis
and the number of errors in calculation are the influences of using a calculator in the tests. If
the scores of the pre-test were significantly greater than post-test, it would have preferred a
deficit of efficiency of concepts. Although, no such trend could be concluded from the
graphs and tables, most of the students have used calculators in the moderate and hard sums.
The necessity and calculator is least in case of easy sums. This refers a requirement
dependent tendency to use calculators amongst student. Proper usage of technology is
suggested, and its credibility is suggested in the study. If majority of the student utilized the
calculator at comparatively easier sums, it might have raised the question of learning
capabilities of the students (Shirley et al., 2011). However, since no such symbols could be
witnessed, we can infer that students do not exercise.
It was also found that use of calculator is effective for all the three levels of
difficulties especially for “Easy” level difficulties of calculation problems.
5.2. Recommendation:
As the analysis proceeded, it is realized that a mediator variable may be more helpful
for testing without calculators. Prior researches showed that use of calculator might increase
the score of mathematical tests of the students specifically when the test involves a large
proportion of computational sums. It is also understood from the most current studies that
legal usage of calculator, utilization of right type of calculator and incorporation of calculator
in mathematical function maximizes the optimistic effect of permitting students to use
calculator on mathematical tests (Drier et al., 2000).

28RESEARCH PAPER
Suitable and integrated usage of technology influences every aspect of mathematics.
The education system should consider what kind of mathematics is to be taught and learned.
Misuse of technology should be discouraged while using calculator (Power and Blubaugh,
2005). Users of calculators must avoid learning multiplication skills and usage of computers
to practice (Dunham and Dick, 1994). Students would be familiar with the use of graphing
calculators and practice too. Simultaneously, teachers would use technology properly and
efficiently in their mathematics classroom if they are common and contented with the
technology (Dion et al., 2001). This research maintains same consideration with many of
previous research topic in this field.

29RESEARCH PAPER
References:
Andrews, A., & Brown, J. (2015). The effects of math anxiety. Education, 135(3), 362-370.
Ansley, T. N., Spratt, K. F., & Forsyth, R. A. (1989). The effects of using calculators to
reduce the computational burden on a standardized test of mathematics problem
solving. Educational and Psychological Measurement, 49, 277-286.
Barton, S. (2000). What does the research say about achievement of students who use
calculator technologies and those who do not. In Fife (Eds.), Electronic Proceedings
of the Thirteenth Annual International Conference on Technology in Collegiate
Mathematics. Atlanta: Addison Wesley.
Bridgeman, B., Harvey, A., & Braswell, J. (1995). Effects of calculator use on scoreson a test
of mathematical reasoning. Journal of Educational Measurement, 32, 323-340.
Chen, J. C., & Lai, Y. L. (2016). A Brief Review of Researching the Graphing Calculator
Used for School Mathematics Classrooms. International Journal of Learning,
Teaching and Educational Research, 14(2).
Colton, D. A. (1997). Monitoring calculator implementation for the ACT and PLAN. Paper
presented at the American Educational Research Association, Chicago, IL.
Deochand, N., Costello, M. S., & Fuqua, R. W. (2015). Phase‐change lines, scale breaks, and
trend lines using Excel 2013. Journal of applied behavior analysis, 48(2), 478-493.
Dion, G., Harvey, A., Jackson, C., Klag, P., Liu, J., & Wright, C. (2001). A survey of
calculator usage in high schools. School Science and Mathematics, 101(8), 427-438.

30RESEARCH PAPER
Doerr, H. M., & Zangor, R. (2000). Creating meaning for and with the graphing calculator.
Educational Studies in Mathematics, 41(2), 143-163.
Drier, H. S., Harper, S., Timmerman, M. A., Garofalo, J., & Shockey, T. (2000). Promoting
appropriate uses of technology in mathematics teacher preparation. Contemporary
Issues in Technology and Teacher Education, 1(1), 66-88.
Dunham, P. H., & Dick, T. P. (1994). Research on graphing calculators. The Mathematics
Teacher, 87(6), 440.
Ellington, A. J. (2003). A meta-analysis of the effects of calculators on students' achievement
and attitude levels in precollege mathematics classes. Journal for Research in
Mathematics Education,34, 433–463.
Etlinger, L. (1974). The electronic calculator: A new trend in school mathematics.
Educational Technology, 14(12), 43-45.
Hembree, R., & Dessart, D.J. (1992). Research on calculators in mathematics education. In
J.T. Fey (Ed.), Calculators in Mathematics Education: 1992 Yearbook of the National
Council of Teachers of Mathematics (pp. 22–31). Reston, VA: NCTM.
Koay, P. L. (2006). Calculator use in primary school mathematics: A Singapore perspective.
The mathematics educator, 9(2), 97-111.
Kutzler, B. (2000). The algebraic calculator as a pedagogical tool for teaching mathematics.
Lloyd, B. H. (1991). Mathematics test performance: The effects of item type and calculator
use. Applied Measurement in Education, 4, 11-22.
Math, H., Lessons, M., Worksheet, I., Decimals, F., Worksheets, 3., & Project, M. et al.
(2018). The Great Debate: The Role of Calculators in Math Education. Math Geek
Mama. Retrieved 9 February 2018, from https://mathgeekmama.com/the-great-
calculator-debate.

31RESEARCH PAPER
Milou, E. (1999). The graphing calculator: A survey of classroom usage. School Science and
Mathematics, 99(3), 133-140.
National Council of Teachers of Mathematics. (2008). The role of technology in the teaching
and learning of mathematics. NCTM News Bulletin, 44(9), 1-12.
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring
mathematical success for all. Reston, VA: Author.
National Council of Teachers of Mathematics. (2015). Strategic use of technology in teaching
and learning mathematics: A position of the National Council of Teachers of
Mathematics. Reston, VA: Author.
Powell, J. (2015). Solve the Following Equation: The Role of the Graphing Calculator in the
Three Worlds of Mathematics. Interpreting Tall's Three Worlds of
Mathematics, 52(2), 11.
Quesada, A.R. (1996). On the impact of the first generation of graphing calculators on the
mathematics curriculum at the secondary level. In P. Gomez & B. Waits (Eds.),
Roles of Calculators in the Classroom (pp. 143-163). Retrieved from
http://ued.uniandes.edu.co/ued/servidor/em/recinf/t g18/ArchivosPDF/
Quesada.pdf
Rakes, C. R., Ronau, R. N., Niess, M. L., Driskell, S., Pugalee, D., & Bush, S. (2011,
January). Research in mathematics instructional technology: Current trends and future
demands. Symposium presented at the annual meeting of the Association of
Mathematics Teacher Educators, Irvine, CA.
Rietveld, T., & van Hout, R. (2015). The t test and beyond: Recommendations for testing the
central tendencies of two independent samples in research on speech, language and
hearing pathology. Journal of communication disorders, 58, 158-168.

32RESEARCH PAPER
Ruthven, K. (1990). The influence of graphic calculator use on translation from graphic to
symbolic forms. Educational studies in mathematics, 21(5), 431-450.
Shirley, M. L., Irving, K. E., Sanalan, V. A., Pape, S. J., & Owens, D. T. (2011). The
practicality of implementing connected classroom technology in secondary
mathematics and science classrooms. International Journal of Science and
Mathematics Education, 9, 459–481.
Simmt, E. (1997). Graphing calculators in high school mathematics. Journal of Computers in
Mathematics and Science Teaching, 16(2), 269-289.
Susskind, J.E. (2005). PowerPoint’s power in the classroom: Enhancing students’ self-
efficacy and attitudes. Computers & Education, 45, 203-215.
Weissgerber, T. L., Milic, N. M., Winham, S. J., & Garovic, V. D. (2015). Beyond bar and
line graphs: time for a new data presentation paradigm. PLoS biology, 13(4),
e1002128.
Wheatley, C. L. (1980). Calculator use and problem-solving performance. Journal for
Research in Mathematics Education, 323-334.

33RESEARCH PAPER
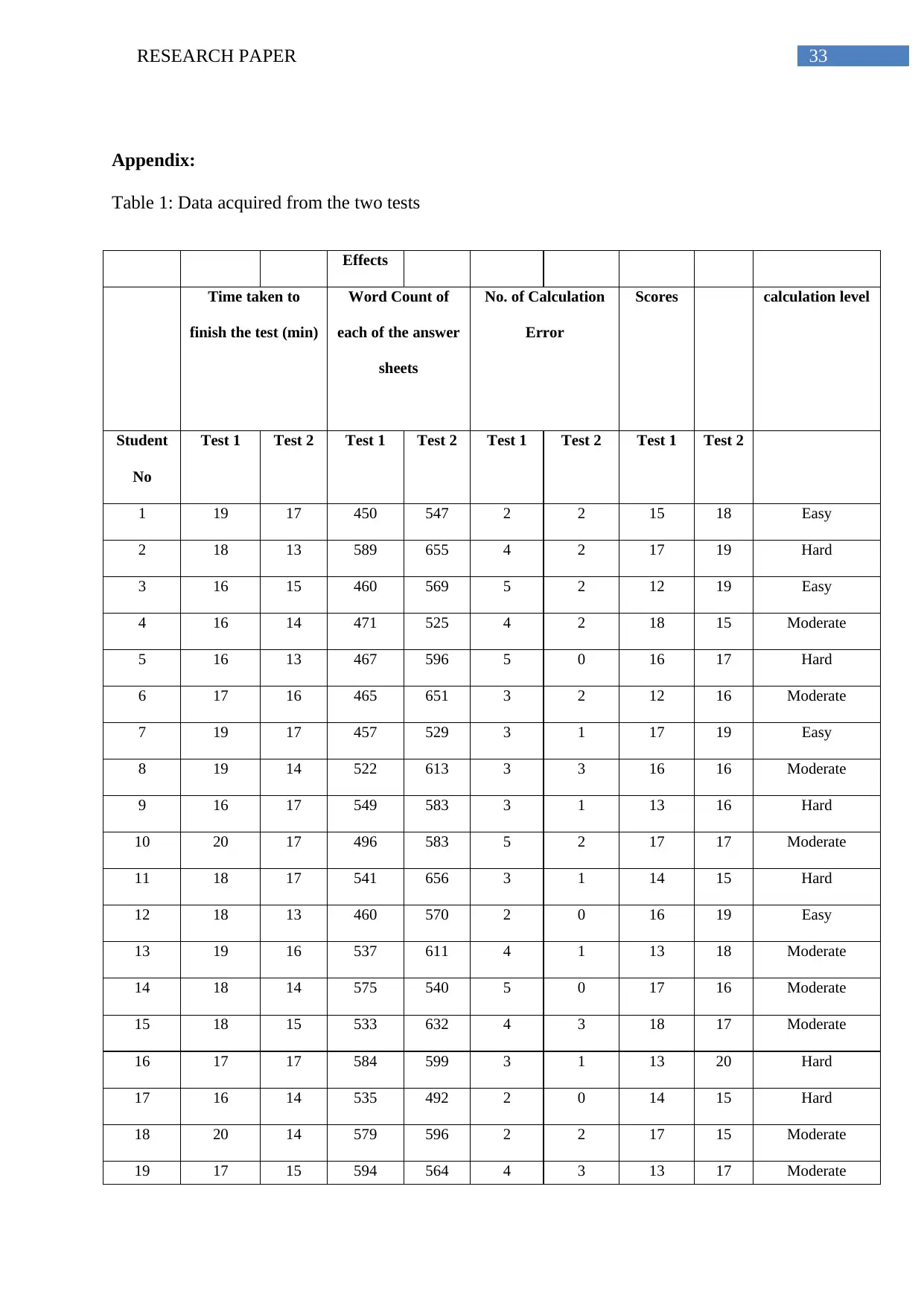
Appendix:
Table 1: Data acquired from the two tests
Effects
Time taken to
finish the test (min)
Word Count of
each of the answer
sheets
No. of Calculation
Error
Scores calculation level
Student
No
Test 1 Test 2 Test 1 Test 2 Test 1 Test 2 Test 1 Test 2
1 19 17 450 547 2 2 15 18 Easy
2 18 13 589 655 4 2 17 19 Hard
3 16 15 460 569 5 2 12 19 Easy
4 16 14 471 525 4 2 18 15 Moderate
5 16 13 467 596 5 0 16 17 Hard
6 17 16 465 651 3 2 12 16 Moderate
7 19 17 457 529 3 1 17 19 Easy
8 19 14 522 613 3 3 16 16 Moderate
9 16 17 549 583 3 1 13 16 Hard
10 20 17 496 583 5 2 17 17 Moderate
11 18 17 541 656 3 1 14 15 Hard
12 18 13 460 570 2 0 16 19 Easy
13 19 16 537 611 4 1 13 18 Moderate
14 18 14 575 540 5 0 17 16 Moderate
15 18 15 533 632 4 3 18 17 Moderate
16 17 17 584 599 3 1 13 20 Hard
17 16 14 535 492 2 0 14 15 Hard
18 20 14 579 596 2 2 17 15 Moderate
19 17 15 594 564 4 3 13 17 Moderate

34RESEARCH PAPER
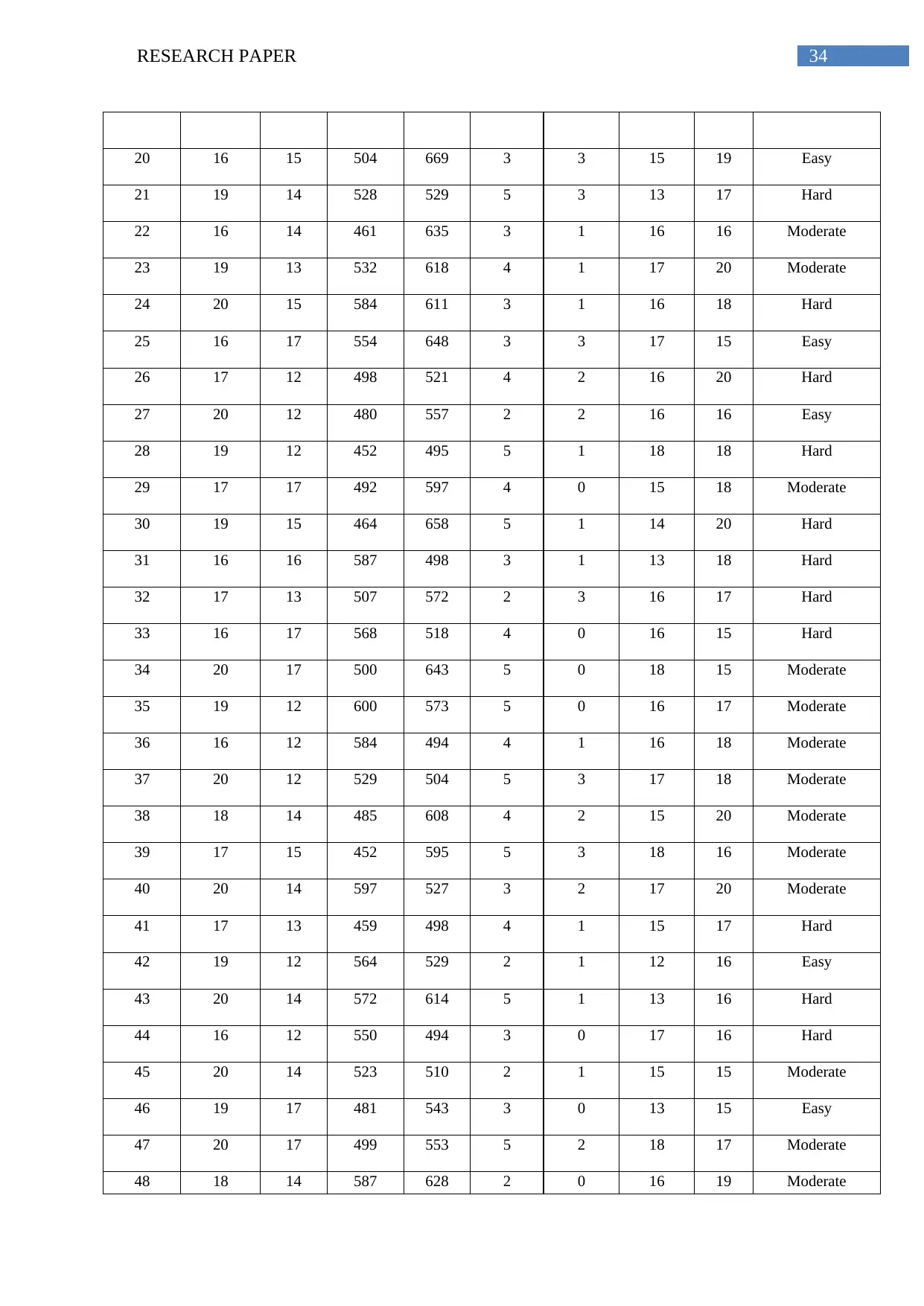
20 16 15 504 669 3 3 15 19 Easy
21 19 14 528 529 5 3 13 17 Hard
22 16 14 461 635 3 1 16 16 Moderate
23 19 13 532 618 4 1 17 20 Moderate
24 20 15 584 611 3 1 16 18 Hard
25 16 17 554 648 3 3 17 15 Easy
26 17 12 498 521 4 2 16 20 Hard
27 20 12 480 557 2 2 16 16 Easy
28 19 12 452 495 5 1 18 18 Hard
29 17 17 492 597 4 0 15 18 Moderate
30 19 15 464 658 5 1 14 20 Hard
31 16 16 587 498 3 1 13 18 Hard
32 17 13 507 572 2 3 16 17 Hard
33 16 17 568 518 4 0 16 15 Hard
34 20 17 500 643 5 0 18 15 Moderate
35 19 12 600 573 5 0 16 17 Moderate
36 16 12 584 494 4 1 16 18 Moderate
37 20 12 529 504 5 3 17 18 Moderate
38 18 14 485 608 4 2 15 20 Moderate
39 17 15 452 595 5 3 18 16 Moderate
40 20 14 597 527 3 2 17 20 Moderate
41 17 13 459 498 4 1 15 17 Hard
42 19 12 564 529 2 1 12 16 Easy
43 20 14 572 614 5 1 13 16 Hard
44 16 12 550 494 3 0 17 16 Hard
45 20 14 523 510 2 1 15 15 Moderate
46 19 17 481 543 3 0 13 15 Easy
47 20 17 499 553 5 2 18 17 Moderate
48 18 14 587 628 2 0 16 19 Moderate

35RESEARCH PAPER
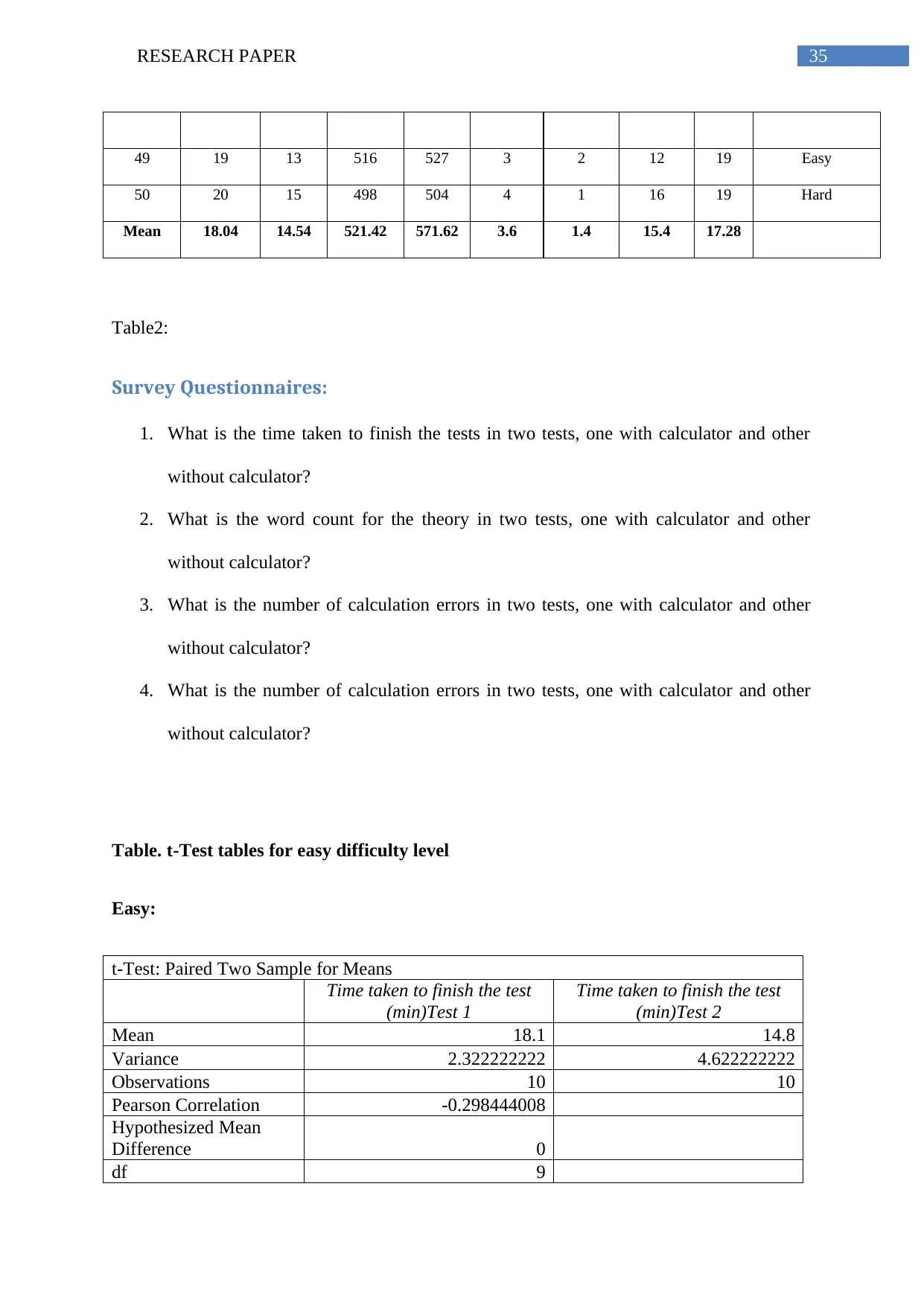
49 19 13 516 527 3 2 12 19 Easy
50 20 15 498 504 4 1 16 19 Hard
Mean 18.04 14.54 521.42 571.62 3.6 1.4 15.4 17.28
Table2:
Survey Questionnaires:
1. What is the time taken to finish the tests in two tests, one with calculator and other
without calculator?
2. What is the word count for the theory in two tests, one with calculator and other
without calculator?
3. What is the number of calculation errors in two tests, one with calculator and other
without calculator?
4. What is the number of calculation errors in two tests, one with calculator and other
without calculator?
Table. t-Test tables for easy difficulty level
Easy:
t-Test: Paired Two Sample for Means
Time taken to finish the test
(min)Test 1
Time taken to finish the test
(min)Test 2
Mean 18.1 14.8
Variance 2.322222222 4.622222222
Observations 10 10
Pearson Correlation -0.298444008
Hypothesized Mean
Difference 0
df 9

36RESEARCH PAPER
t Stat 3.497993004
P(T<=t) one-tail 0.003372388
t Critical one-tail 1.833112923
P(T<=t) two-tail 0.006744777
t Critical two-tail 2.262157158
t-Test: Paired Two Sample for Means
Word count for theory Test
1
Word count for theory Test
2
Mean 492.6 568.8
Variance 1671.822 2501.066667
Observations 10 10
Pearson Correlation 0.268058
Hypothesized Mean
Difference 0
df 9
t Stat -4.34428
P(T<=t) one-tail 0.000933
t Critical one-tail 1.833113
P(T<=t) two-tail 0.001866
t Critical two-tail 2.262157
t-Test: Paired Two Sample for Means
No. of calculation error Test
1
No. of calculation error Test
2
Mean 2.8 1.6
Variance 0.844444 1.155555556
Observations 10 10
Pearson Correlation 0.247457
Hypothesized Mean
Difference 0
df 9
t Stat 3.086975
P(T<=t) one-tail 0.006496
t Critical one-tail 1.833113
P(T<=t) two-tail 0.012993
t Critical two-tail 2.262157
t-Test: Paired Two Sample for Means
Scores Test 1 Scores Test 2
Mean 14.5 17.5
Variance 4.277777778 3.166666667

37RESEARCH PAPER
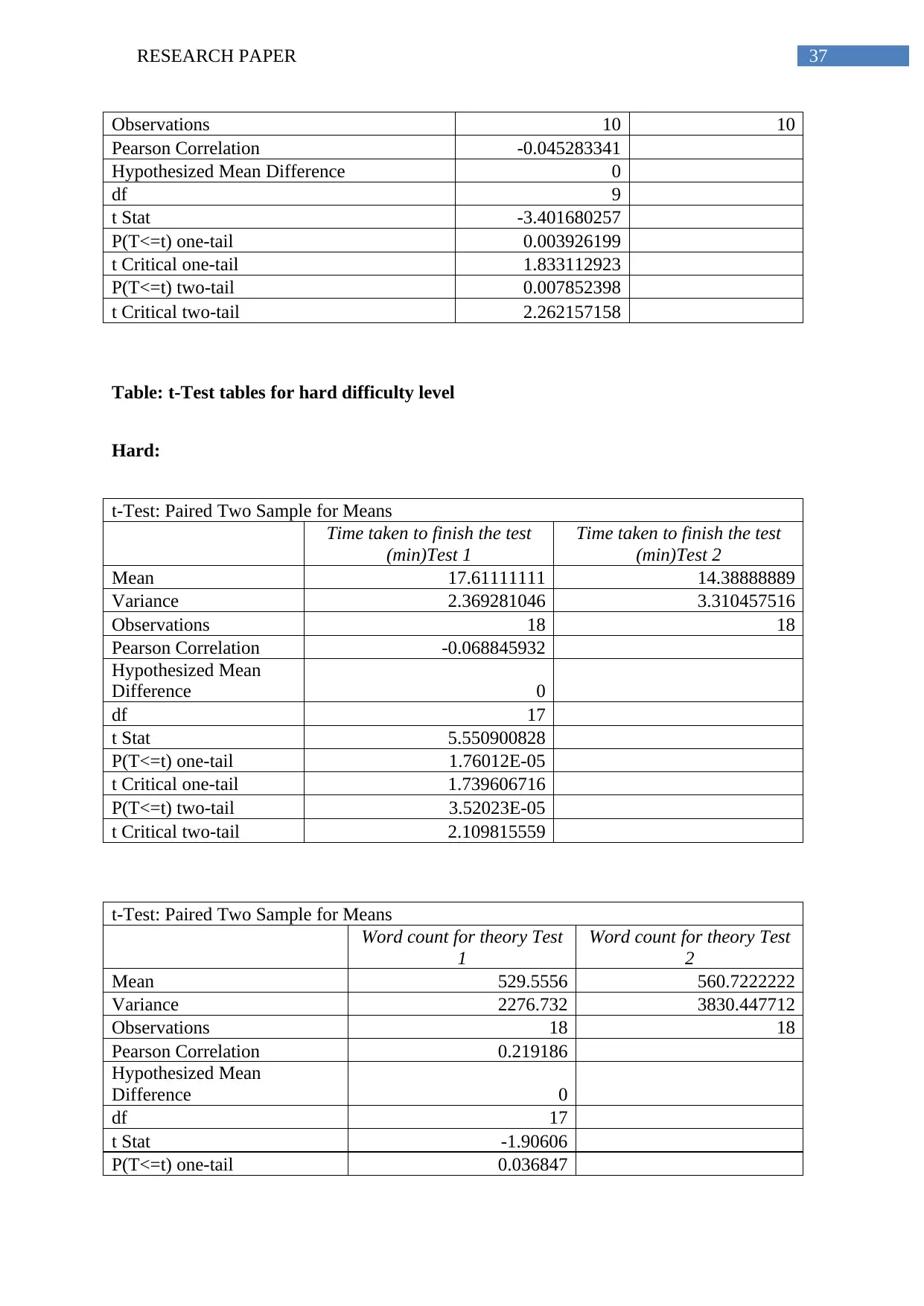
Observations 10 10
Pearson Correlation -0.045283341
Hypothesized Mean Difference 0
df 9
t Stat -3.401680257
P(T<=t) one-tail 0.003926199
t Critical one-tail 1.833112923
P(T<=t) two-tail 0.007852398
t Critical two-tail 2.262157158
Table: t-Test tables for hard difficulty level
Hard:
t-Test: Paired Two Sample for Means
Time taken to finish the test
(min)Test 1
Time taken to finish the test
(min)Test 2
Mean 17.61111111 14.38888889
Variance 2.369281046 3.310457516
Observations 18 18
Pearson Correlation -0.068845932
Hypothesized Mean
Difference 0
df 17
t Stat 5.550900828
P(T<=t) one-tail 1.76012E-05
t Critical one-tail 1.739606716
P(T<=t) two-tail 3.52023E-05
t Critical two-tail 2.109815559
t-Test: Paired Two Sample for Means
Word count for theory Test
1
Word count for theory Test
2
Mean 529.5556 560.7222222
Variance 2276.732 3830.447712
Observations 18 18
Pearson Correlation 0.219186
Hypothesized Mean
Difference 0
df 17
t Stat -1.90606
P(T<=t) one-tail 0.036847

38RESEARCH PAPER
t Critical one-tail 1.739607
P(T<=t) two-tail 0.073694
t Critical two-tail 2.109816
t-Test: Paired Two Sample for Means
No. of calculation error Test
1
No. of calculation error Test
2
Mean 3.722222 1.111111111
Variance 1.035948 0.810457516
Observations 18 18
Pearson Correlation 0.035665
Hypothesized Mean
Difference 0
df 17
t Stat 8.300879
P(T<=t) one-tail 1.1E-07
t Critical one-tail 1.739607
P(T<=t) two-tail 2.2E-07
t Critical two-tail 2.109816
t-Test: Paired Two Sample for Means
Scores Test 1 Scores Test 2
Mean 15 17.38888889
Variance 2.705882353 2.95751634
Observations 18 18
Pearson Correlation 0.124762566
Hypothesized Mean Difference 0
df 17
t Stat -4.551977701
P(T<=t) one-tail 0.000141282
t Critical one-tail 1.739606716
P(T<=t) two-tail 0.000282563
t Critical two-tail 2.109815559
Table: t-Test tables for moderate difficulty level
Moderate:
t-Test: Paired Two Sample for Means
Time taken to finish the test
(min)Test 1
Time taken to finish the test
(min)Test 2

39RESEARCH PAPER
Mean 18.36363636 14.54545455
Variance 2.147186147 2.545454545
Observations 22 22
Pearson Correlation 0.114805366
Hypothesized Mean
Difference 0
df 21
t Stat 8.784930279
P(T<=t) one-tail 8.89571E-09
t Critical one-tail 1.720742871
P(T<=t) two-tail 1.77914E-08
t Critical two-tail 2.079613837
t-Test: Paired Two Sample for Means
Word count for theory Test
1
Word count for theory Test
2
Mean 527.8636 581.8181818
Variance 2342.314 2312.727273
Observations 22 22
Pearson Correlation -0.33858
Hypothesized Mean
Difference 0
df 21
t Stat -3.20595
P(T<=t) one-tail 0.002122
t Critical one-tail 1.720743
P(T<=t) two-tail 0.004244
t Critical two-tail 2.079614
t-Test: Paired Two Sample for Means
No. of calculation error Test
1
No. of calculation error Test
2
Mean 3.863636 1.545454545
Variance 1.075758 1.212121212
Observations 22 22
Pearson Correlation 0.026537
Hypothesized Mean
Difference 0
df 21
t Stat 7.285714
P(T<=t) one-tail 1.78E-07
t Critical one-tail 1.720743
P(T<=t) two-tail 3.57E-07

40RESEARCH PAPER
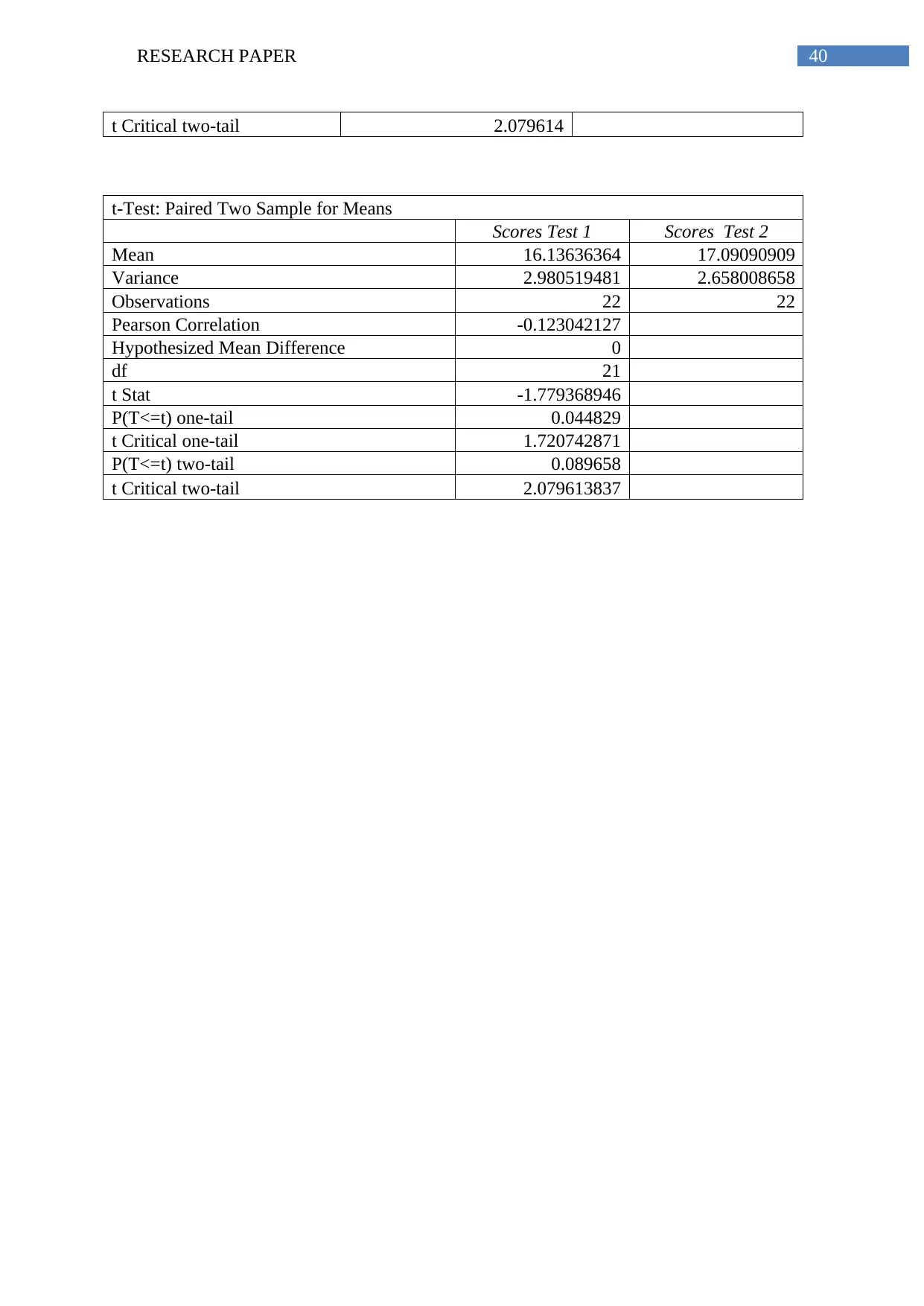
t Critical two-tail 2.079614
t-Test: Paired Two Sample for Means
Scores Test 1 Scores Test 2
Mean 16.13636364 17.09090909
Variance 2.980519481 2.658008658
Observations 22 22
Pearson Correlation -0.123042127
Hypothesized Mean Difference 0
df 21
t Stat -1.779368946
P(T<=t) one-tail 0.044829
t Critical one-tail 1.720742871
P(T<=t) two-tail 0.089658
t Critical two-tail 2.079613837