MATH 22981 Winter 2020: Differential Calculus Assignment 2 Solutions
VerifiedAdded on 2022/08/17
|7
|476
|12
Homework Assignment
AI Summary
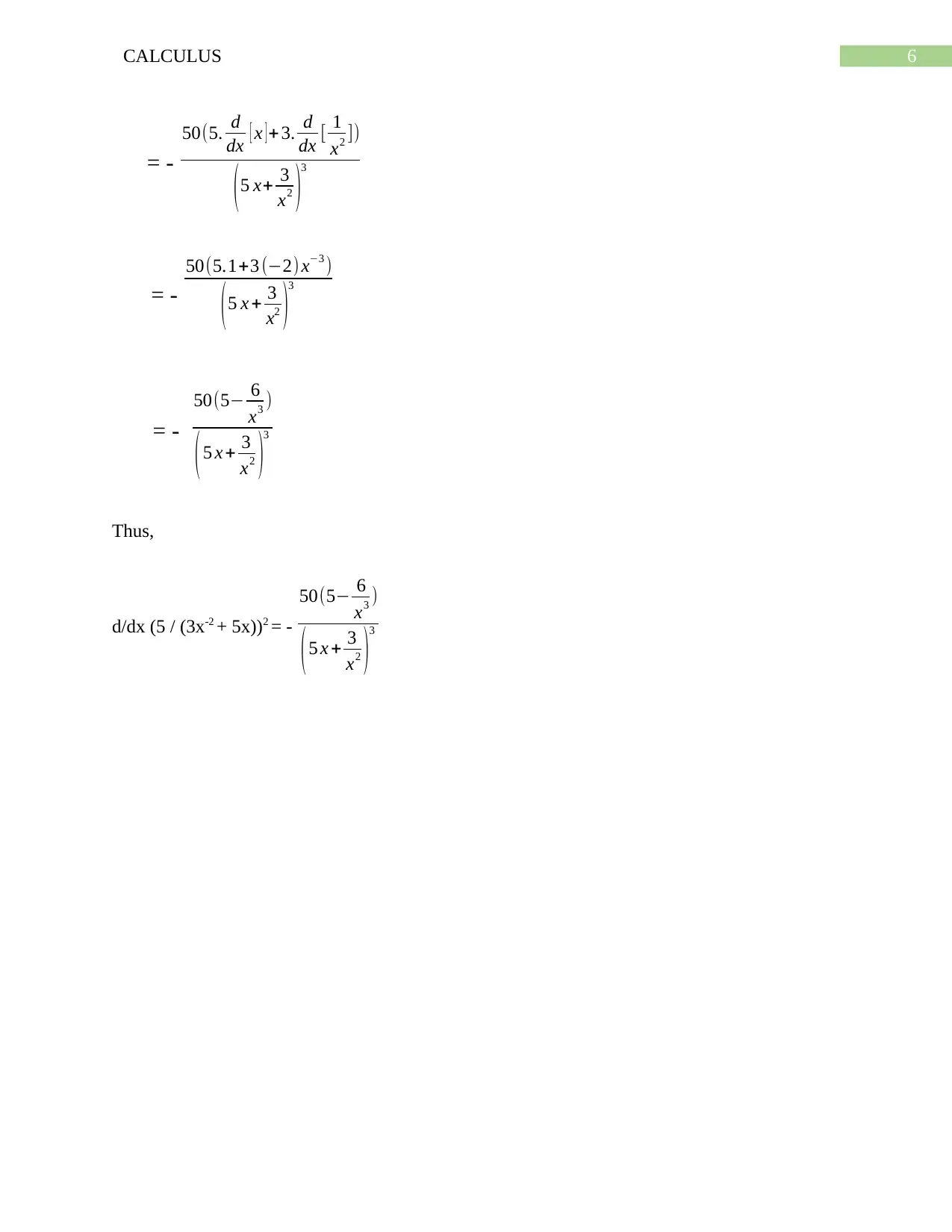
This document presents the solutions to a Calculus assignment focusing on differential calculus concepts. The assignment includes three main problems. The first problem requires finding the equation of a tangent line to a curve at a given point using the limit definition of the derivative. The second problem involves evaluating the slope of a tangent line using the power law rule. The third problem asks for the evaluation of three different derivatives, applying various differentiation techniques such as the power rule and product rule. The solutions are presented step-by-step, demonstrating the application of calculus principles to solve the problems effectively.
1 out of 7













![[object Object]](/_next/static/media/star-bottom.7253800d.svg)