Calculus Assignment: Displacement, Acceleration, Kinetic Energy, Charge and Volume Calculations

This assignment covers topics such as displacement, acceleration, kinetic energy, charge and volume calculations in calculus. It includes examples and calculations for each topic.

CALCULUS ASSIGNMENT
By Name
Course
Instructor
Institution
Location
Date

Part A
(a) An expression of the displacement X of the mass is given as the integral of the
velocity.
X=ʃv; X=∫
0
10
0.8 sin ( 8 t )
(b) The displacement of the mass during the interval of the time from 0 to 3π/16 seconds.
X= ∫
0
3 π /16
0.8 sin ( 8 t )
0.8[-cos8]03π/16
=149cm
(c) An expression of the acceleration is given as a derivative of the velocity Stenger 2012
Acceleration, a= dv
dt
(d) The acceleration of the mass will be calculated as follows
=dv/dt(0.8sin8t)
The derivative of sine is cosine
=8*cos 4.712;
=-0.0031118ms-2 the negative value implies deceleration of the mass.
(e)The coordinates of the maxima and minima; at the maximum point, the derivative of x
with respect to t is zero. This implies that dx/dt=0 but dx/dv=Velocity.
0=0.8sin(8t); t=0 and therefore the cooirdinate3s of the points is at (0,1) for maximum and
(0,0)

F) Kinetic energy is given by 1/2mv2 but V=0.8sin(8t), this follows that the kinetic energy
can be expressed as K. E=1/2m[0.8sin(8t)]2
(g) The co ordinate of the maxima and minima as per the equation of the K.E are obtained by
equating the derivative of the entire equation to erode/dt=0 and this gives the coordinates as
(0,0) for the minimum and (1,2.3) for the maximum. The coordinates of the point of inflexion
is (1,2.3).
(h) The coordinates of the points of the maximum and minimum point for the Gravitational
potential Energy will be obtained by getting the derivative of the equation GPE=mg(0.3+X)
but X is the integral of the equation 0.8sin (8t) Trefethen and Weideman 2014 This means
that the required equation becomes 0=mg(o.3+0.8sin8t). The derivative of this function gives
the coordinates as (0.53.0.2) for the maximum and (0,0.2) as the minimum values. The
turning point is (0.50,0.1).
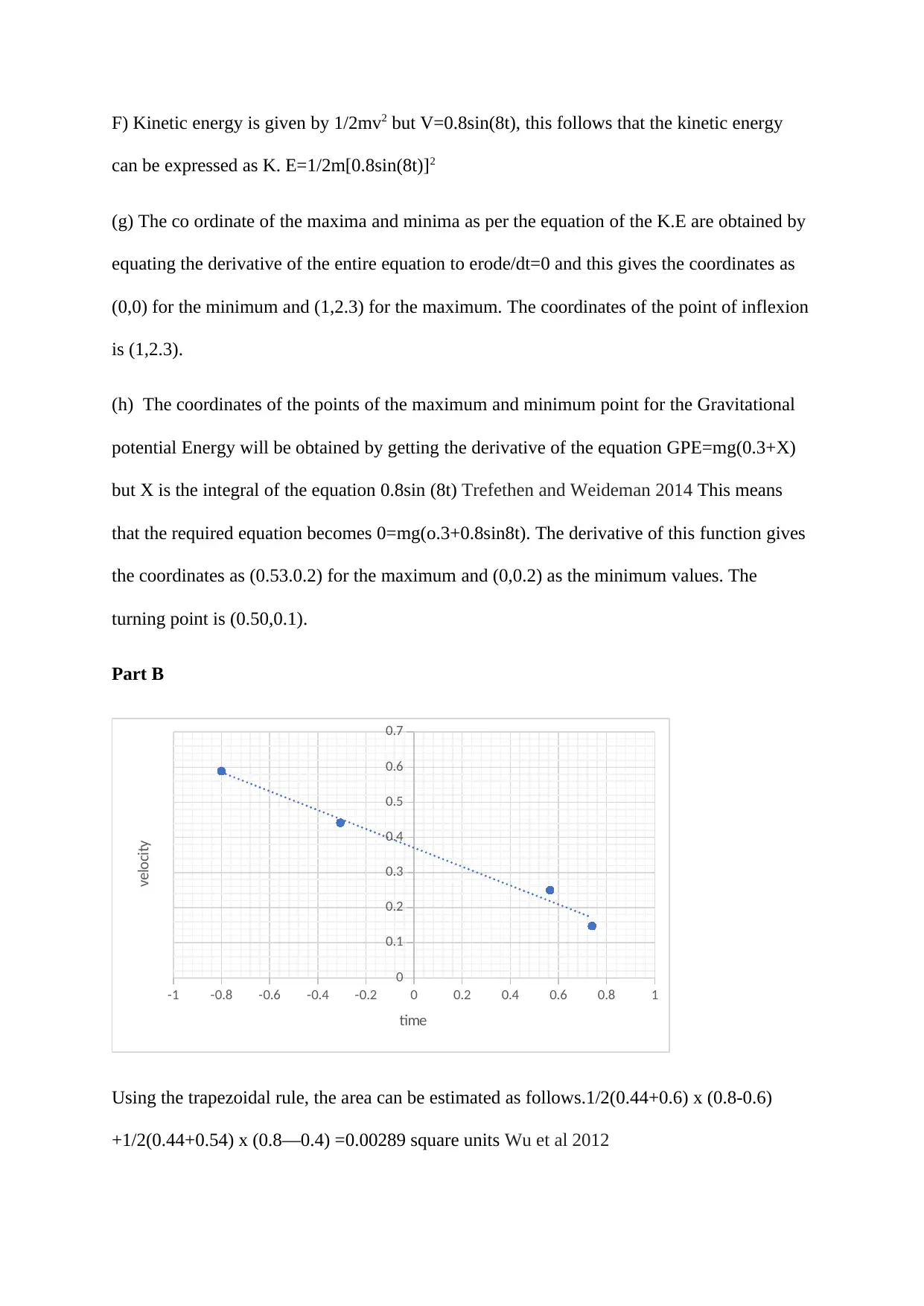
Part B
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
time
velocity
Using the trapezoidal rule, the area can be estimated as follows.1/2(0.44+0.6) x (0.8-0.6)
+1/2(0.44+0.54) x (0.8—0.4) =0.00289 square units Wu et al 2012

Part C
(a)The mass that is attached to the spring has undergone several oscillatory motions starting
from the lowest level possible depending on the distance that is moved Trefethen et al 2014.
When the mass is pulled downwards, the displacement is observed as the string stretches
downwards. This displacement is reduced as the spring seeks to regain its original shape and
size. This pattern continues thus oscillatory motion is achieved. The mass therefore is
displaced from the giddiest
point to the least point as illustrated in the sketches below.
The velocity of the mass will equally vary during this oscillatory motion. Just before the mass
is pulled downwards, the initial velocity is recorded and when the downward motion is just
about to end, final velocity is obtained Mazandarani and Kamyad 2013 This variation in the
velocity leads to acceleration and deceleration of the mass during the motion. The
deceleration is very significant in the upward motion.
(b)The relationship between the displacement and the acceleration is obtained through
integration. The second integral of the acceleration will give the displacement.
X= ∬
0
3 π /16
a.The equation obtained can be used to relate the displacement and the acceleration of
any object under oscillatory motion.
Question Two
Part A
(a) The current value at t=0 is obtained or calculated as follows=It;

12x10-6=Ix0; which means I=Q/t and therefore the value of current at t=0 is infinity. Also, at
t=5 the value of the charge is 0.4414 coulombs.
Since Q=It; 0.4414=Ix5 and therefore I=0.4414/5 which is equal to 0.08828A.
(b) The value of the current reduces with time. This could be as a result of the increased
resistance within the circuit Mazandarani.
Part B
In the second diagram when the resistor is exchanged the value of the current is calculated as
shown below=It but Q =0.6592 coulombs. The current therefore is 0.6592/5 which is equal to
0. 1318A.The initial value of the current was equally very low. The value of the current
reduces as the time increases.
Part C
When the divisor K is reduced, the value of the charge increases Javed and Trefethen 2014
The value of the current increases since the two variables are directly proportional to one
another. Also, when the value of the K is increased, the value of the charge will reduce.
Increases in the value of the charge means a corresponding increase in the value of the
current considering that the time is kept constant.
Solids and shapes
Part A
(a)Assuming the solid sphere is a rectangle that turns into the cylinder upon rotation, the
volume is obtained ads shown below Gabrielsson and Weiner2012
Volume of the cylinder=π ∫
1
9
¿ ¿

V=π∫
1
9
3 dy this integration gives the answer as 54π cubic units.
(b)When the rotation is done a long the y axis, the answer obtained is 86π cubic units. The
difference of the two volumes becomes 32 cubic units. This implies that the rotation along the
Y axis gives greater volume as indicated above Gabrielsson and Weiner 2012
Part B
(a)Taking the function as f(x)= (2/3) x and integrating across the values of [0.3];
1/3x2 30|=1/3(3)2-0=3
Volume of the cone is calculated as 1/3πr2h, r=2 and the h=3 thus the volume becomes 1/3πr
(2)2x3
=4π
When the rotation is done along the y axis, the volume becomes

The radius of the cone becomes 3 while the height changes to 2 and therefore the volume is π
(3)2(2) -(1/3)2(2) =the volume of the rotated area Bathe and Noh 2012.
=12π in cubic units
(c) When the rotation is done along the Y axis, the volume increases and the difference in the
volume is obtained as 12π-8π. The variation of the value is 4 cubic units. This therefore
means that rotation along the Y axis gives a bigger volume compared to the rotation along the
X-axis.

References
Bathe, K.J. and Noh, G., 2012. Insight into an implicit time integration scheme for structural
dynamics. Computers & Structures, 98, pp.1-6.
Gabrielsson, J. and Weiner, D., 2012. Non-compartmental analysis.
Javed, M. and Trefethen, L.N., 2014. A trapezoidal rule error bound unifying the Euler–
Maclaurin formula and geometric convergence for periodic functions. Proc. R. Soc.
A, 470(2161), p.20130571.
Mazandarani, M. and Kamyad, A.V., 2013. Modified fractional Euler method for solving
fuzzy fractional initial value problem. Communications in Nonlinear Science and Numerical
Simulation, 18(1), pp.12-21.
Stenger, F., 2012. Numerical methods based on sinc and analytic functions (Vol. 20).
Springer Science & Business Media.
Trefethen, L.N. and Weideman, J.A.C., 2014. The exponentially convergent trapezoidal
rule. SIAM Review, 56(3), pp.385-458.
Wu, Y.W., Bauer, L.A., Ballard, R.A., Ferriero, D.M., Glidden, D.V., Mayock, D.E., Chang,
T., Durand, D.J., Song, D., Bonifacio, S.L. and Gonzalez, F.F., 2012. Erythropoietin for
neuroprotection in neonatal encephalopathy: safety and pharmacokinetics. Pediatrics, 130(4),
pp.683-691.