Calculus Assignment: Solving Equations, Arcs, and Graph Analysis
VerifiedAdded on 2023/06/15
|6
|666
|475
Homework Assignment
AI Summary
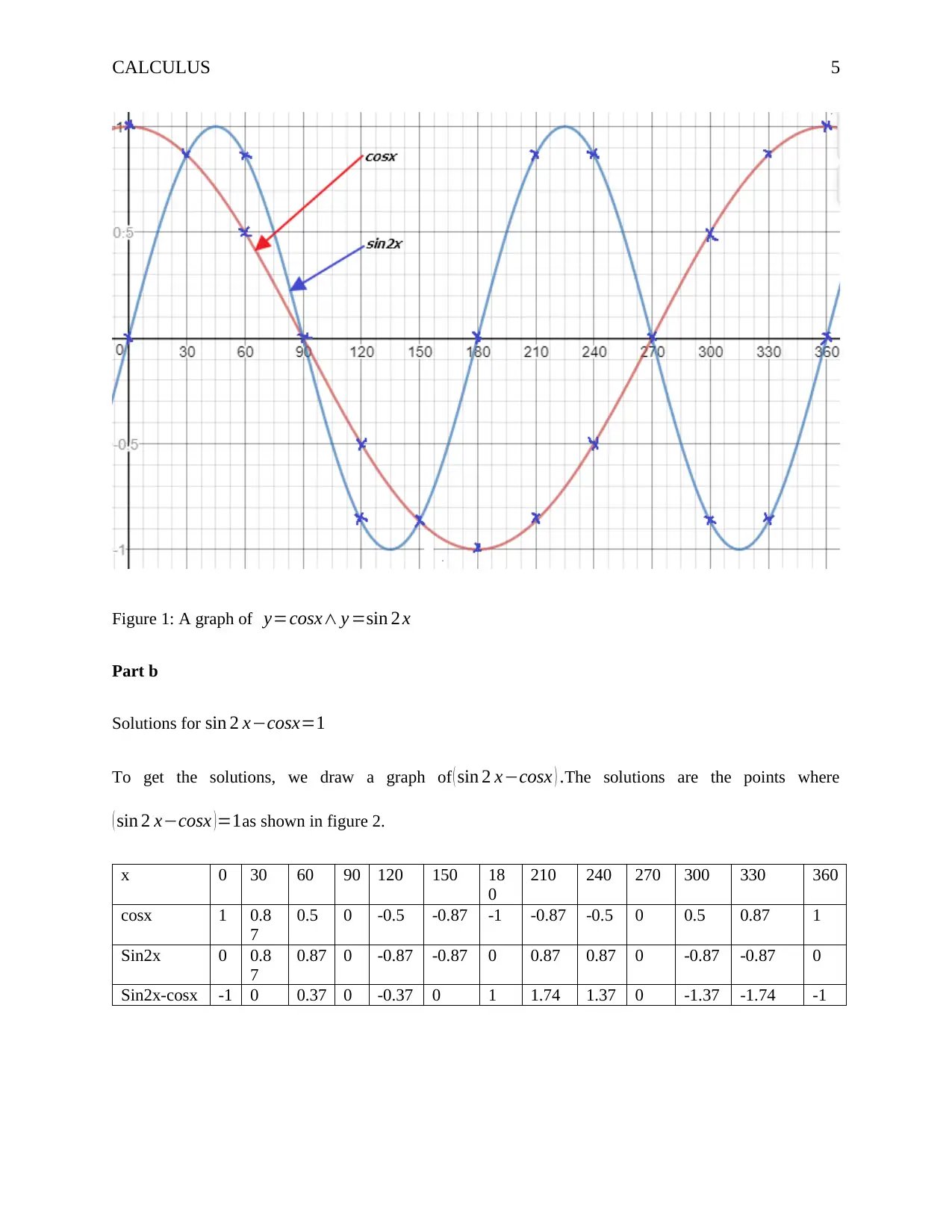
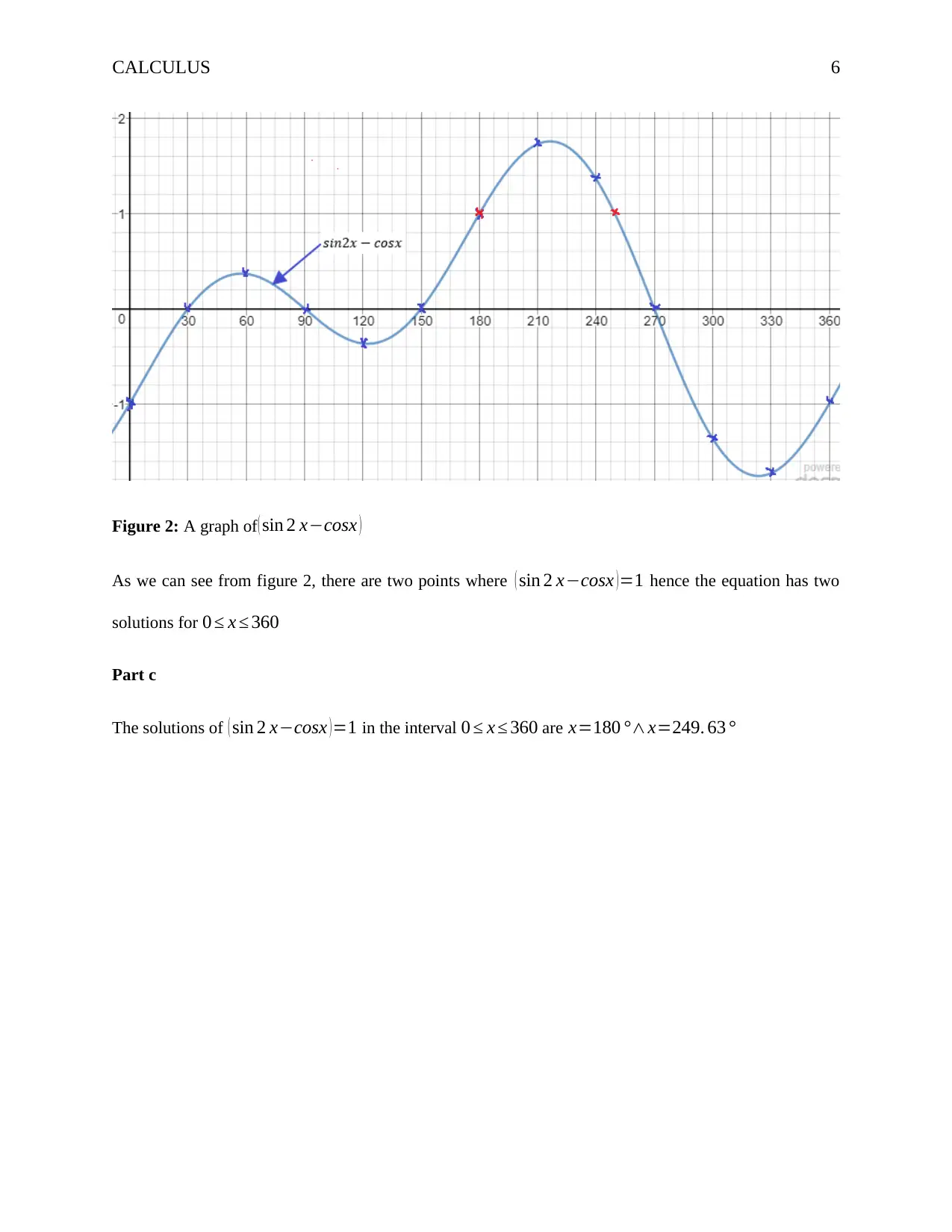
This Calculus assignment provides detailed solutions to several problems involving trigonometric functions and equations. The first question focuses on calculating the area of a sector and the difference in arc lengths. The second question involves solving trigonometric equations, including finding solutions for θ within specified ranges. The assignment also includes graphical analysis, where the student plots y=cosx and y=sin2x on the same axes and determines solutions for the equation sin2x - cosx = 1 by identifying points where the graphed function equals 1. The solutions for x are provided in degrees. Desklib offers a wide range of similar solved assignments and study resources for students.
1 out of 6








![MATH130: Algebra Assignment 2 Solution - [University Name] - May 2019](/_next/image/?url=https%3A%2F%2Fdesklib.com%2Fmedia%2Fimages%2Fmf%2Ff5e9dd638f934d7d8421c8edf334793d.jpg&w=256&q=75)

![[object Object]](/_next/static/media/star-bottom.7253800d.svg)