Calculus

This article covers various topics in Calculus such as differentiation, integration, optimization, and more. It includes solved problems with step-by-step solutions. The article also provides insights into finding the maximum and minimum values of a function, calculating the area under a curve, and determining the population growth rate. The content is relevant for students studying Calculus in college or university.

Running head: CALCULUS
Calculus
Name of the Student:
Name of the University:
Author’s note:

1CALCULUS
Table of Contents
Answer 1....................................................................................................................................2
Part a (The quotient rule to differentiate):..............................................................................2
Part b (Chain rule to differentiate):........................................................................................2
Part c (Differentiation):..........................................................................................................2
Answer 2....................................................................................................................................2
Part a.......................................................................................................................................2
Part b......................................................................................................................................3
Part c.......................................................................................................................................3
Answer 3....................................................................................................................................3
Part a.......................................................................................................................................3
Part b......................................................................................................................................4
Part c.......................................................................................................................................4
Answer 4....................................................................................................................................5
Part a.......................................................................................................................................5
Part b......................................................................................................................................5
Part c.......................................................................................................................................5
Answer 5....................................................................................................................................5
Part a.......................................................................................................................................5
Part b......................................................................................................................................6
Answer 6....................................................................................................................................6

2CALCULUS
Part a.......................................................................................................................................6
Part b......................................................................................................................................7
Answer 7....................................................................................................................................7
Integral by parts:....................................................................................................................7

3CALCULUS
Answer 1.
Part a (The quotient rule to differentiate):
y = (2 x4−3 x )
(4 x−1)
If the defined two functions f(x) and g(x) are differentiable, then the quotient is differentiable
and, ( f
g )'
=( f ' g−fg '
g2 ).
Here, f = (2x4-3x), g = (4x -1).
Therefore, y’ = ( 2 x4 −3 x
4 x−1 )' =
( 4 x−1 )∗d
dx ( 2 x4−3 x )− ( 2 x4−3 x )∗d
dx (4 x−1)
( 4−x )2
=
( 4 x−1 )∗( 8 x3−3 ) − ( 2 x4−3 x )∗4
( 4−x ) 2
= [ 8 x3−3
4−x − 4 x ( 2 x2−3 )
( 4−x )2 ].
Part b (Chain rule to differentiate):
y = 6cos (x3 + 3)
If f(x) and g(x) are both differentiable, then – F’(x) = f ‘(g(x)) g’(x).
Here, g(x) = (x3+3), f(x) = 6 cos x
So, g‘(x) = 3x2, f’(x) = (-6 sin x)
F ‘(x) = f ‘(g(x)) g’ (x) = f ‘(x3) g’(x) = (- 6 sin(x3+3))*(3x2) = (-18 x2 sin(x3+3)).
Part c (Differentiation):
y = ( 4 x2 −e2 x ¿ sin 3 x
Now, y’ = d
dx (4 x2−e2 x )sin 3 x = sin 3 x d
dx ( 4 x2−e2 x ) + ( 4 x2 −e2 x ) d
dx (sin 3 x )
= sin 3 x∗
{( d
dx 4 x2
)− ( d
dx e2 x
) }+ ( 4 x2−e2 x )∗3 cos (3 x)
= sin 3 x∗( 8 x−2 e2 x)+ ( 4 x2−e2 x ) ∗3 cos (3 x)
= ( 8 x−2 e2 x ) sin 3 x +3 ( 4 x2−e2 x ) cos 3 x.

4CALCULUS
Answer 2.
Part a
The angular displacement is θ radians. The equation of spoke of a wheel is –
θ = 0.5t4– t3, where ‘t’ is the time in seconds.
The angular velocity after 2 seconds is, dθ
dt ∨¿t=2=[ ( 0.5∗4 t4−1−3 t3−1 ) ]∨¿ ¿t=2= [(2t3 – 3t2)] |
t=2
= (2*8-3*4) = (16-12) = 4 radian/sec.
Part b
The angular acceleration is, d2 θ
d t2 = d
dt ( d θ
dt ) = d
dt ( 2 t3−3 t2 ) =¿ radian/sec2.
The angular acceleration after 3 seconds is = 6*3(3-1) radian/sec2 = 6*6 radian/sec2 = 36
radian/sec2.
Part c
Angular acceleration is 0.
Hence, 6 t ( t−1 ) =0
Or, t = 0, 1.
Therefore, at the starting of moving of spoke, the angular acceleration is 0. Also, after 1
second of the angular displacement, the angular acceleration is 0.
Answer 3.
The length and width of metal sheet is 120 mm and 75 mm respectively. Equal squares of
side x are cut from each of the corners. The remaining flaps are then folded upwards to form
an open-ended box.
Part a
Figure 1: Rectangular metal sheet

5CALCULUS
120 mm
x mm x mm
1st square 2nd square
First Flip
x mm x mm
75 mm Fourth Second
Flip Base of the box Flip
x mm x mm
Third Flip
3rd square 4th square
x mm x mm
Part b
The length of the base of the box will be (120-x-x) mm = (120-2x) mm.
The width of the base of the box will be (75-x-x) mm = (75-2x) mm.
The height of the box = x mm.

6CALCULUS
Therefore, the volume of the box = length*width*height
= (120-2x) mm. * (75-2x) mm. * x mm.
= x*(9000 -150x -240x+4x2) mm3.
= x*(9000 - 390x+4x2) mm3. = (9000x – 390x2 + 4x3) mm3.
Part c
We must find the value of x for which volume (V) is maximum.
V = 9000x – 390x2 + 4x3
or, dV
dx = d
dx ( 9000 x−390 x2+4 x3 )= d
dx ( 9000 x )− d
dx ( 390 x2 ) + d
dx ( 4 x3)
or, dV
dx =( 9000−780 x +12 x2 )
The first derivative should be 0. Hence, dV
dx =0
Hence, (9000-780x+12x2) = 0,
or, x = 50, 15 (solving the quadratic equation).
The value of x cannot be 50 as in this case the width of base of the box (75-2x) will be
negative. It is impossible and absurd. So, we reject x=50 and accept x=15.
The volume of the open-ended box is maximum when x=15 mm. It shows that the volume of
the box is (9000*15 – 390* 152 + 4* 153) mm3 = (135000 –87750 + 13500) mm3= 60750
mm3.
Answer 4.
Part a
∫(5 x2 + √ x− 4
x2 ¿) dx=∫ 5 x2 dx+¿∫ x
1
2 dx ¿ ¿ -∫ 4
x2 dx
=( 5
( 2+ 1 ) x2+1
+
1
( 1
2 )+1
x (1
2 )+1
- 4
(−2+1) x−2+1
)
= ( 5
3 x3+
1
3
2
x
3
2
– 4
( −1 ) x−1
)= ( 5
3 x3 + 2
3 x
3
2 +4x−1) = ( 5 x3
3 + 2 x √ x
3 + 4
x ¿ .

7CALCULUS
Part b
∫¿ ¿= ∫cos ( x
2 )dx - ∫sin ( 3 x
2 )dx= 2 sin ( x
2 )- (−2
3 )cos (3 x
2 )
=2 sin ( x
2 )+ 2
3 cos ( 3 x
2 ).
Part c
∫
1
5
s
√ s2+ 4 ds
Let, √ (s2 +4) = k, or, s2 + 4 = k2, or, s2 = k2- 4,
or, 2sds = 2kdk, or, dk = 2 sds
2 k =sds.
Now, ∫
1
5
s
√ s2+ 4 ds = ∫
1
5 ( s∗s)
k dk =∫
1
5
s2
k dk = ∫
1
5 ( k2−4)
k dk = ∫
1
5
(k dk + 4
k ¿ dk )¿
= ∫
1
5
k dk +∫
1
5
4
k dk =¿+4*¿
= ( 25
2 −1
2 ¿+4∗(log5−log 1) = [ 24
2 +4∗log(5
1 ¿)¿ = (12 + 4*log 5) = (12+4*0.69897) = (12+
2.79588) = 14.79588.
Answer 5.
Part a
The area bounded by the curve y ¿ 1
x between x = 2 and x = 6 is –
∫
a
b
y dx = ∫
2
6
( 1
x ) dx= ¿ = (log6 – log2) = log ( 6
2 ¿ = log3 = 0.778 (approximately).
Part b
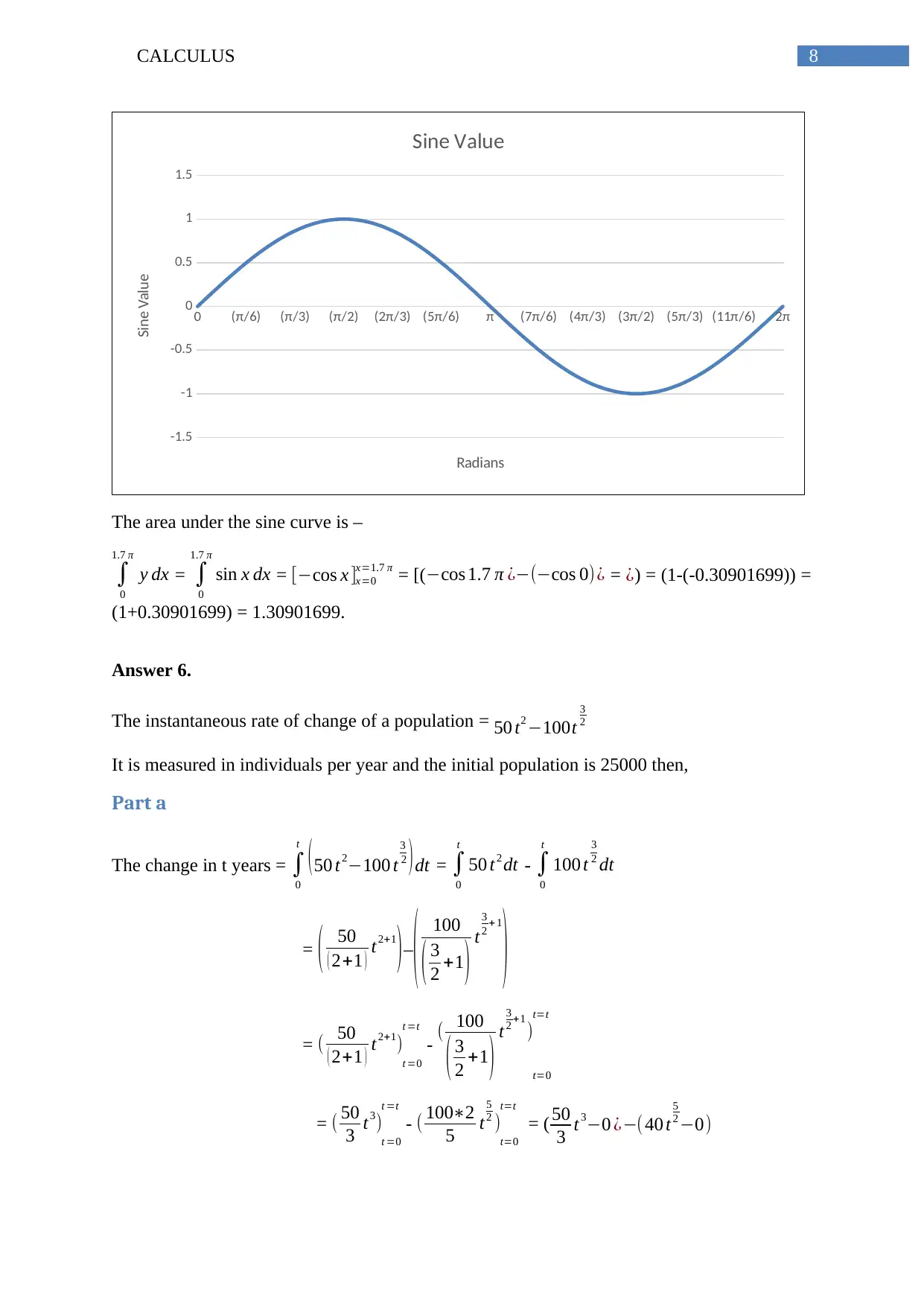
Figure 2: The Sine Curvein the range 0 to 2π

8CALCULUS
0 (π/6) (π/3) (π/2) (2π/3) (5π/6) π (7π/6) (4π/3) (3π/2) (5π/3) (11π/6) 2π
-1.5
-1
-0.5
0
0.5
1
1.5
Sine Value
Radians
Sine Value
The area under the sine curve is –
∫
0
1.7 π
y dx = ∫
0
1.7 π
sin x dx = [−cos x ]x=0
x=1.7 π = [(−cos 1.7 π ¿−(−cos 0)¿ = ¿) = (1-(-0.30901699)) =
(1+0.30901699) = 1.30901699.
Answer 6.
The instantaneous rate of change of a population = 50 t2 −100t
3
2
It is measured in individuals per year and the initial population is 25000 then,
Part a
The change in t years = ∫
0
t
(50 t2−100 t
3
2 )dt = ∫
0
t
50 t2 dt - ∫
0
t
100 t
3
2 dt
= ( 50
( 2+1 ) t2+1
)–
( 100
( 3
2 +1 ) t
3
2 + 1
)
= ( 50
( 2+1 ) t2+1)t =0
t =t
- ( 100
( 3
2 +1 ) t
3
2 +1
)
t=0
t=t
= ( 50
3 t3)t =0
t =t
- ( 100∗2
5 t
5
2 )t=0
t=t
= ( 50
3 t3−0 ¿−( 40 t
5
2 −0)

9CALCULUS
= ( 50
3 t3- 40 t
5
2 ¿
Therefore, the population after ‘t’ years is – (initial population + total population)
= (25000 + ( 50
3 t3
- 40 t
5
2 ¿) = (25000 + 50
3 t3
- 40 t
5
2 ¿.
Part b
The increased population after 25 years = ( 50
3 ∗253−40∗25
5
2 ¿ = (260417 – 125000)
= 135417
Hence, the total population after 25 years would be = (25000 + 135417) = 160417.
Answer 7
Integral by parts:
∫5 x cos ( 4 x ) dx = [5 x∫cos ( 4 x ) dx- ∫ ( cos 4 x ) dx . d
dx ( 5 x ) dx]
= [5x* sin ( 4 x)
4 ¿ - ∫¿ ¿ = 5 x sin (4 x )
4 −20∫sin (4 x ) dx
= 5 x sin ( 4 x )
4 −¿( −20
( 4+ 1 ) cos (4 x ) ¿
= ( 5 x sin( 4 x)
4 +4 cos 4 x ).