Calculus Assignment: Rate of Change, Integration, and Maxima/Minima
VerifiedAdded on 2023/01/09
|12
|910
|100
Homework Assignment
AI Summary
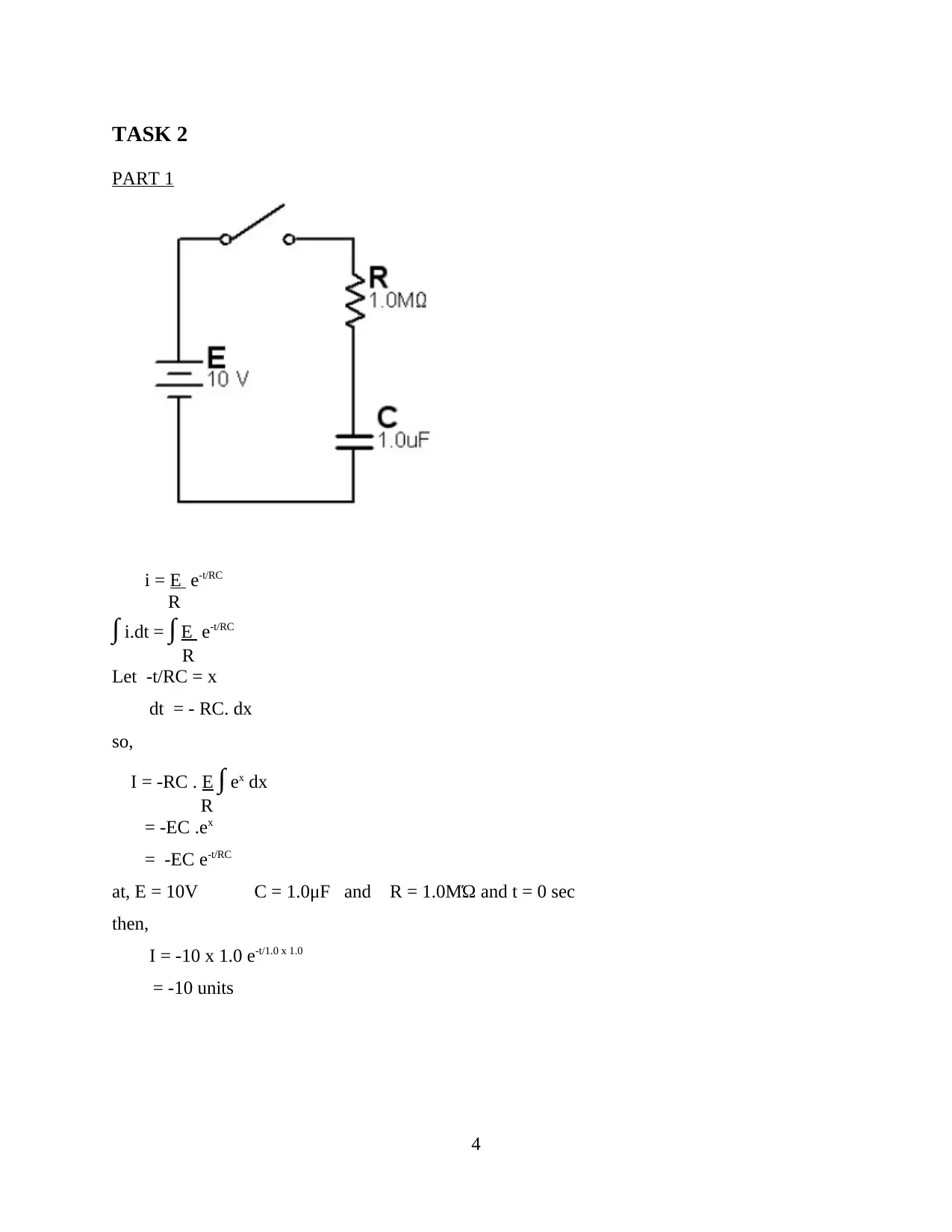
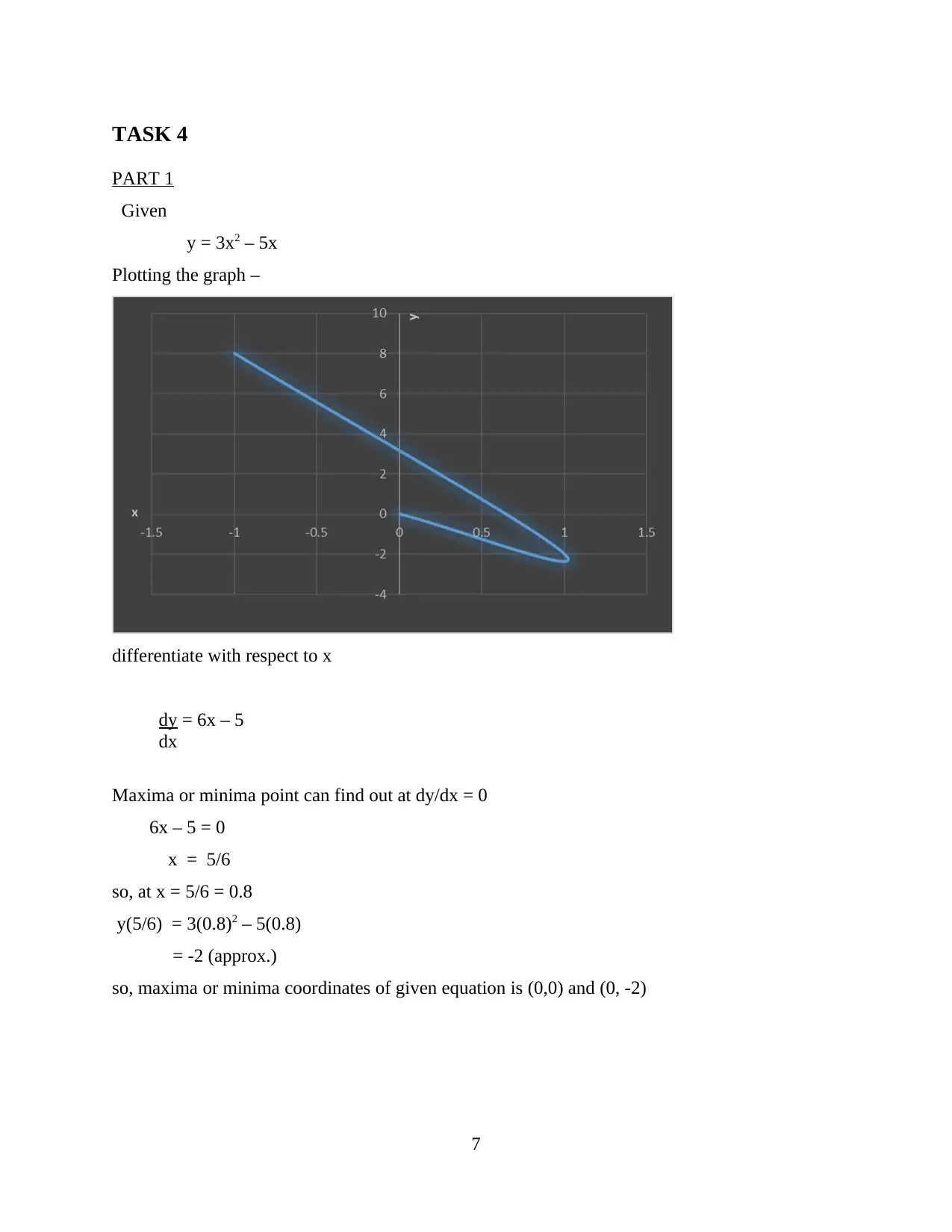
This calculus assignment covers various applications of differentiation and integration. Task 1 focuses on determining the rate of change of voltage using differentiation, with examples involving different voltage functions. Task 2 explores integration, calculating the integral of a current function over time and finding the current value. Task 3 involves definite integration to calculate areas under curves. Finally, Task 4 focuses on finding maxima and minima of given functions and plotting their graphs. The assignment demonstrates the application of calculus concepts to solve practical problems. The solutions are step-by-step and include calculations for different scenarios involving voltage, current, and areas under curves. The assignment provides a comprehensive overview of calculus concepts and their applications.
1 out of 12
















![[object Object]](/_next/static/media/star-bottom.7253800d.svg)