Calculus I Assignment: Derivatives, Applications, and Analysis

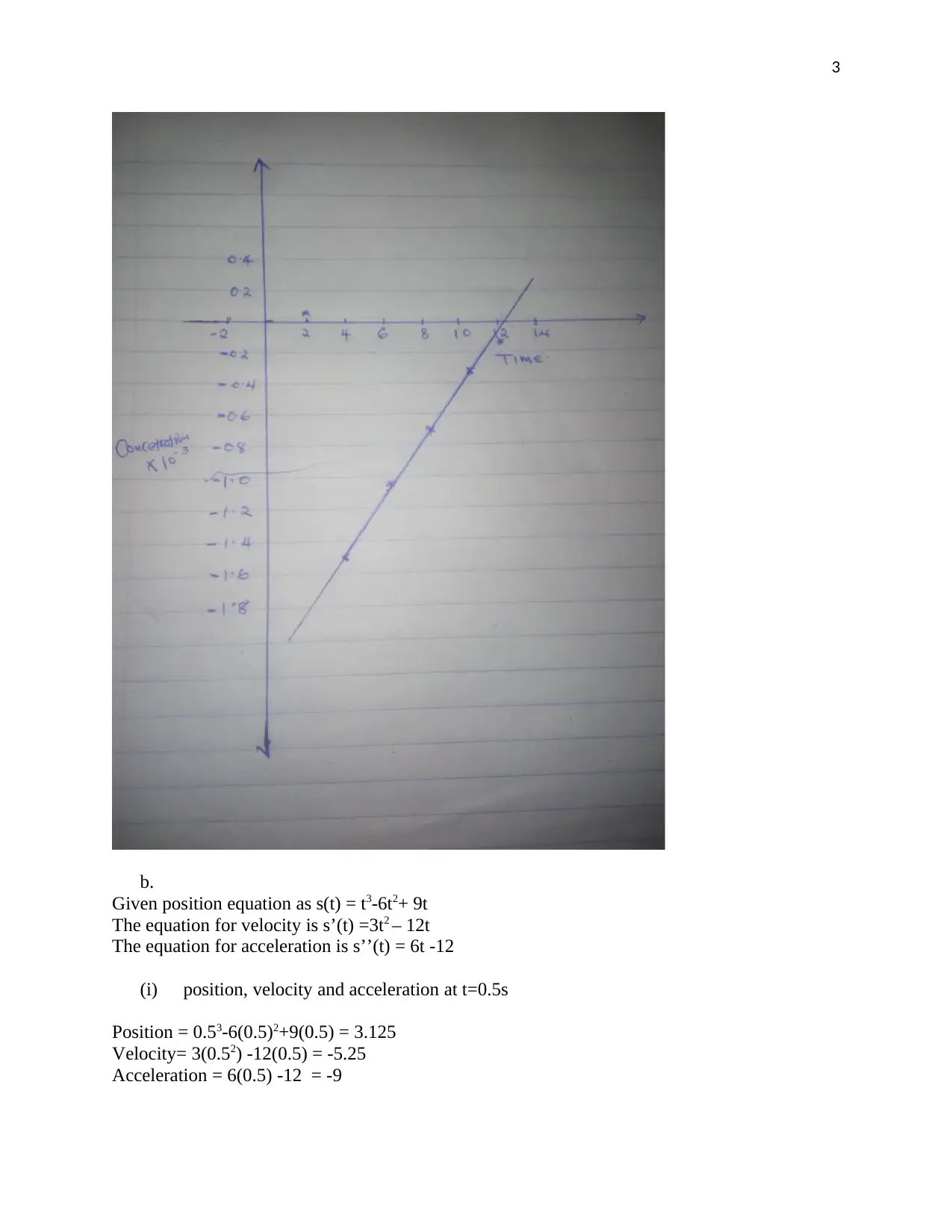
This calculus assignment solution covers a range of topics including derivatives, rate of change, and applications of calculus. It begins by finding the rate of change of nitrate concentration using the quotient rule and calculating the concentration at a specific time. It also includes graphical representation based on provided values. The assignment further delves into finding position, velocity, and acceleration at given time intervals. Solved problems include applications of the product rule and chain rule for differentiation, involving functions like ln(x), trigonometric functions, and exponential functions. Finally, the assignment determines stationary points of a given function by finding its first and second derivatives and solving for critical points. Desklib offers more solved assignments and past papers for students.

1
Name:
Course:
Professor:
Date:

2
Question 1
a.
c ( t ) = t
16 t2 +10 t+63
(i) Rate of change of nitrate
Using quotient rule;
c ' ( t ) =(16 t¿ ¿2+10 t +63) ( 1 ) −t(32 t−10)
¿ ¿ ¿
c ' ( t ) =16 t2 +10 t+63−32t2−10 t
¿ ¿
c ' ( t ) =−16 t2 +63
¿ ¿
(ii) Concentration after 2 hrs
Replacing in the c’(t)
Concentration will be
c' (2)=−16 x 22 +63
¿ ¿
= -4.63-5
(iii) graphical representation using the following values
Time Concentration (x10-3)
2 -0.0463
4 -1.50
6 -1.05
8 -0.706
10 -0.495
12 -0.362

3
b.
Given position equation as s(t) = t3-6t2+ 9t
The equation for velocity is s’(t) =3t2 – 12t
The equation for acceleration is s’’(t) = 6t -12
(i) position, velocity and acceleration at t=0.5s
Position = 0.53-6(0.5)2+9(0.5) = 3.125
Velocity= 3(0.52) -12(0.5) = -5.25
Acceleration = 6(0.5) -12 = -9

4
(ii) position, velocity and acceleration at t =4s
position = 43-6(4)2+9(4) = 4
velocity= 3(42) -12(4) = 0
acceleration = 6(4) -12 = 12
(iii) whether the object is accelerating or decelerating
the object is accelerating on the above timelines. Initially, the object comes from deceleration
rate which is indicated by negative acceleration rate at 0.5s to a positive acceleration rate at 4s.
Question 2
a.
Using product rule
(2*ln(x))'
(2)'*ln(x) + 2*(ln(x))'
0*ln(x) + 2*(ln(x))'
0*ln(x) + 2*(1/x)
=2/x
b.
(x + 4)(x + 4)
Using product rule
(x + 4)’(x + 4) + (x + 4)(x + 4)’
(1)*(x + 4) + (x + 4)*(1)
X + 4 + x + 4
= 2x +8
c.
Sin(3x +2)
Using chain rule;
Take sin(3x + 2) to be sin u where u = 3x + 2
F’(u) = cos u and u’ = 3
Therefore solution will be

5
= cos u * 3
= cos(3x+2)*3
= 3cos(3x+2)
d.
6sin2x +3x2 -5e3x
Differentiating the three parts separately;
Solving 6sin2x
Let the part be 6sinu, where u= 2x
The derivative of 6sinu = 6cosu
While that of u = 2
Therefore it turns to be 6cos2x*2 = 12cos2x
Derivative of 3x2 = 6x
The derivative of 5e3x
Taking the equation to be 5eu where u = 3x and u’ =3
The derivative will be 5eu*3
=15e3x
Combining the derivatives
12cos2x + 6x - 15e3x
e.
(3x + 7)(e-ax)
Using product rule to differentiate;
(3x+7)’(e-ax) + (3x+7)( e-ax)’
(3x+7)’ = 3
(e-ax)’ = -ae-ax
Therefore;

6
3(e-ax) + (3x+7)(-ae-ax)
= 3e-ax -3axe-ax -7ae-ax
= (3-3ax-7a)e-ax
f.
sinax
2−cosx
( 2−cosx ) ( sinax ) ' − ( sinax ) ( 2−cosx )'
(2−cosx )2
( 2−cosx )(acosax )− ( sinax ) ( sinx)
(2−cosx)2
( 2 acosax−acos2 x ) −sinax∗sinx
(2−cosx )2
Question 3
a.
F(x) = x3+3x-2
The derivative for the slope = 3x2+3
When f’(x) =2
3x2+3 =2
3x2 = -1
X2 = -1/3
b. (i)
F(x) = -2x3+9x2-12x-7
F’(x) = -6x2+18x-12
F’’(x) = -12x +18
Rearranging the results by factoring 6
=6(-2x+3)

7
= 6(3-2x)
(ii)
The station points can be found through equating f’(x) =0
F’(x) = -6x2+18x-12
-6x2+18x-12 = 0
Using the quadratic equation to solve the problem;
x=−b ± √ b2−4 ac
2 a
x=−18 ± √182−4 (−6 ) (−12)
2 (−6)
x=−18 ± √ 324−288
−12
x=−12± √ 36
−12
x=−18 ±6
−12
The values of x= 2 or 1
Using the equation -2x3+9x2-12x-7 to find the y values, the stationary points will be at
When x =2, y = -11 therefore the point = (2,-11)
When x =1, y =-12 therefore the point is (1,-12)

8