Calculus Assignment: Derivative Calculations, Graph Analysis, and More
VerifiedAdded on 2023/06/10
|4
|693
|302
Homework Assignment
AI Summary
This calculus assignment solution addresses problems related to derivatives and their applications. Question 1 focuses on the chain rule and derivative calculations using given functions and graphs. Question 2 analyzes the truth or falsity of statements about derivatives, requiring the student to provide proofs or counterexamples. Finally, Question 3 involves interpreting a velocity-time graph to determine the farthest distance of a bicyclist from a lake, requiring the calculation of displacement using the area under the curve. The solution demonstrates a strong understanding of calculus concepts, including differentiation rules, graph analysis, and the interpretation of physical applications of derivatives.
1 out of 4
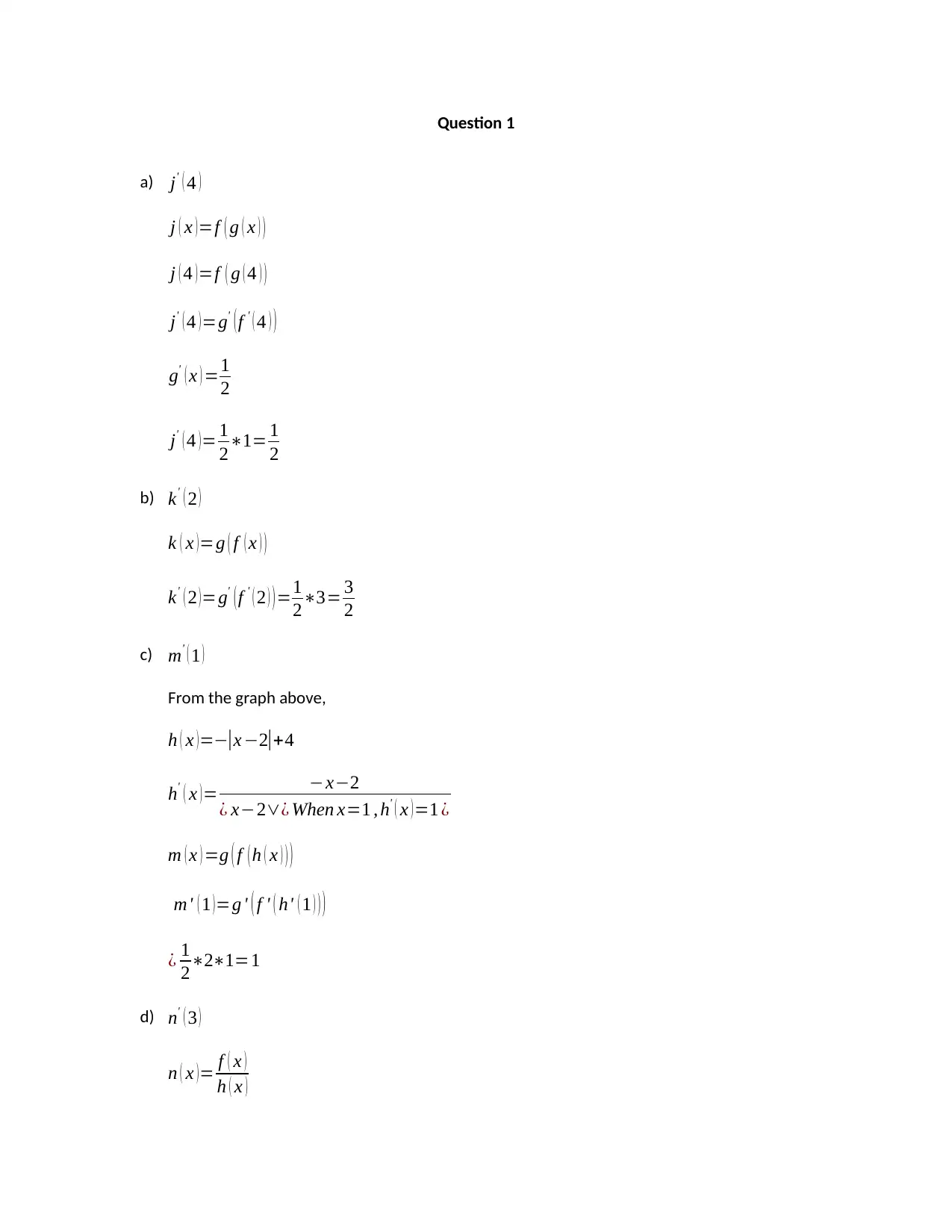










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)