Calculus Assignment Solution: University Level Problems

This document presents a complete solution to a calculus assignment, addressing a variety of problems. The solutions cover topics such as finding the point on a line closest to the origin, determining perpendicular unit vectors, calculating angles between vectors in a molecule, working with coordinate...Read More

CALCULUS
Student id
[Pick the date]

Question 1
Let
Vector 1=a
Vector 2=v
Point located on the line ( a+ tv ) which is near to the origin in such as way that a ┴ v .
a ┴ vonly when the dot product would be equal to zero.
a . v =0
Line equation ¿ a+ t v
The distance (t , a+t v) from origin (0, 0) would be determined as shown below:
¿ √ ( a−c ) 2+ ¿ ¿
a=a , b=a+tv ,c =0 , d=0
¿ √ ( t−0 ) 2 +¿ ¿
¿ √ t2 +¿ ¿
Now,
let
1

f ( x )= √t2 +¿ ¿
It is essential to minimize the square of the distance and hence,
g ( x )=t2+¿
The next step is to determine the first derivative of f ( x ) .
d
dx f ( x )= d
dx ¿
¿ t +v (a+tv)
√t2+¿ ¿ ¿
Further, find the first derivative of g ( x )
d
dx g ( x ) = d
dx t2 +¿
¿ 2 t+¿
Let the value of denominator close to zero.
t2+ ¿0 (derivative is defined)
t=0 , a+tv=0∨t=−a
v
This is termed as critical point of the and therefore, point (−a
v ,0 ¿
is not close to the origin.
2

Question 2
All unit vectors which are perpendicular to the vector ( 5
12 )=?
Let the vector is a = 5i +12 j
Two vectors would be termed as perpendicular to each other when their dot product would be
equal to zero.
cos θ= a . b
|a||b|
θ=90 ° ( perpendicular )
a . b
|a||b|
=cos 90=0
a . b=0
Assume that vector (ai+bj) is perpendicular to (5i +12 j).
Now,
¿ ( ai+bj ) .(5 i+ 12 j)
3

5 a+12 b=0 … … …… . ( 1 )
In order to determine the unit vector which would be perpendicular to the (5i +12 j) hit and trial
method needs to be applied.
at a=12 , b=−5
( 5∗12 )+ ( 12∗−5 ) =0 satisfied
u1= 12i−5 j
√ ( 12 )2+ (−5 )2 =( 12i
13 − 5 j
13 )
At a=−12, b=5
¿
u2= −12 i+ 5 j
√ (−12 )2 + ( 5 )2 =(−12 i
13 + 5 j
13 )
Hence, the two unit vectors i.e. ( 12i
13 − 5 j
13 ) and ( −12i
13 + 5 j
13 ) are perpendicular to ( 5
12 ) .
Question 3
Angle between any of the two line segment from carbon atom to hydrogen atom =?
4

Let a be the vector along AC∧b be the vector along CD .
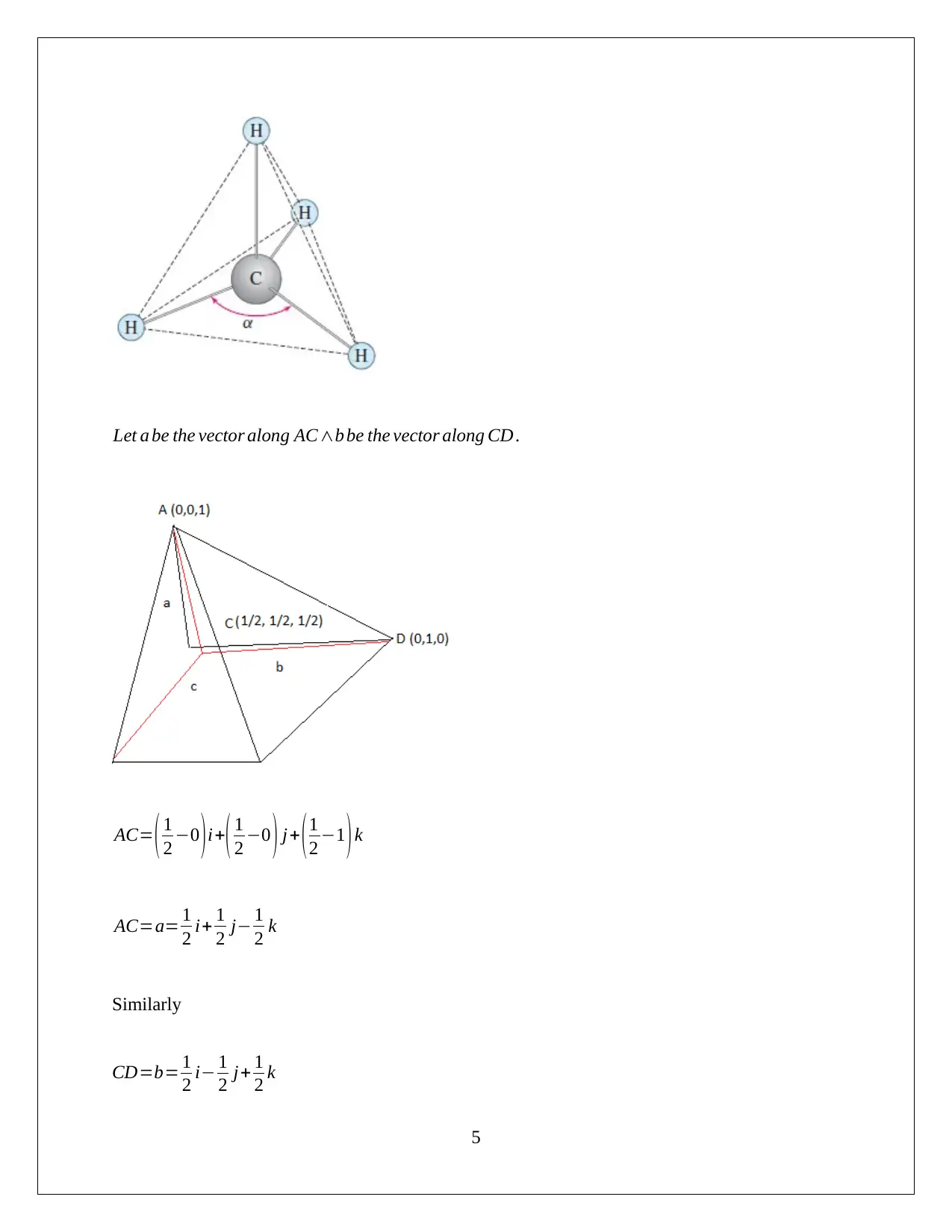
AC= ( 1
2 −0 )i+( 1
2 −0 ) j+ (1
2 −1 )k
AC=a= 1
2 i+ 1
2 j− 1
2 k
Similarly
CD=b= 1
2 i− 1
2 j+ 1
2 k
5

Now
cos θ= a . b
|a||b|
cos θ= ( 1
2 i+ 1
2 j− 1
2 k ) . ( 1
2 i− 1
2 j+ 1
2 k )
√ ( 1
2 )
2
+( 1
2 )
2
+(−1
2 )
2
√ (1
2 )
2
+( −1
2 )
2
+( 1
2 )
2
¿
1
4 − 1
4 − 1
4
√ 3
4 √ 3
4
¿
−1
4
3
4
¿− 4
12
cos θ=−1
3
θ=cos−1
(−1
3 )
θ=121.6 °
Hence, the angle would be 121.60.
6

Question 4
Given figure
Let the center of the systemO(0,0,0)
And the corner would be A ( ± 1, ± 1, ± 1 )
Hence, the by co-ordinate system as per the figure is highlighted below:
OA= (−1i+1 j+1 k )
OB= (−1 i+ 1 j−1 k )
OA .OB = ( −1i+1 j+1 k ) . ( −1 i+1 j−1 k )
¿ 1+1−1=1
Hence,
|OA|= √ (−1)2 +(1)2+(1)2= √ 3
7

|OB|= √ (−1)2+(1)2 +(−1)2 = √ 3
Now,
OA .OB =|OA||OB|cos β
cos β= OA .OB
|OA||OB|
cos β= 1
√3 × √3 = 1
3
β=cos−1
( 1
3 )
β=78.36 °
Question 5
It is given that P and Q points are located in R3.
The aim is to prove that R is the midpoint of PQ only when X is equidistant from P and Q and
XR is orthogonal to PQ.
Let the X = ( x , y , z )
Point X is equidistance from P and Q and hence, vector XR is orthogonal to PQ.
8

XR . PQ=0…………….. (1)
Here,
XR=XO +¿
Hence,
XR . PQ=0
( XO +¿ ¿ . PQ=0
XO . PQ +¿ . PQ=0
( −OX ) . PQ +¿ . PQ=0
OX . PQ=¿ . PQ … … …… … …… .. ( 2 )
Further,
PQ=PO+ OQ
R is midpoint of PQ and hence, ¿= PQ
2 = OP+OQ
2
9

From equation (2)
OX . PQ=¿ . PQ
OX . PQ=( OP +OQ
2 ).(PO +OQ)
PO=−OP
OX . PQ=( OP +OQ
2 ) .( OQ−OP )
OX . PQ= 1
2 (OP2−OQ2)
This is the equation of the plan on which x lies and hence, the above assumptions that X is
equidistance from P and Q and hence, vector XR is orthogonal to PQ. Also, R is the midpoint of
PQ and therefore, P and Q points are located in R3 .
Question 6
Cross product
10

¿ (2
0
0 )× (−1
0
1 )
¿
¿ ( 2 0 0 ) × ( −1 0 1 )
Rule of cross product of the two vectors
¿ ( 0.1−0.0 0.(−1)−2.1 2.0−0.(−1) )
¿ ( 0−0 0−20−0 )
¿ ( 0−2 0 )
¿ (−
0
2
0 )
11

Question 7
Cross product
¿ (1
1
0 )× (0
1
1 )
¿
¿ ( 1 10 ) × ( 01 1 )
Rule of cross product of the two vectors
¿ ( 1.1−0.1 0.0−1.11.1−1.0 )
¿ ( 1−00−1 1−0 )
¿ ( 1−1 1 )
¿ (−
1
1
1)
12

Question 8
Given figure
Based on the above figure it can be concluded that option (b) and (c) would form a right-handed
system.
Answer: ( c ) { v , u , w } ∧ ( b ) { w , v , u }
13

Question 9
Given vectors are
(3
1
1 )∧ (−1
2
1 )
¿
¿ ( 3 11 ) ∧ ( −12 1 )
 The first step is to determine the cross product of these two vectors.
¿ ( 3 11 ) × (−1 2 1 )
Rule of cross product of the two vectors
¿ ( 1.1−1.2 1.(−1)−3.1 3.2−1.(−1) )
¿ ( 1−2−1−3 6+1 )
¿(−1−4 7)
14

¿ ( −
−1
4
7 )
 The first step is to determine the unit vector
u= (−1−4 7 )
√¿ ¿ ¿
u= (−1−4 7 )
√66
u=
( −1
√ 66 , −4
√66 , 7
√66 )
Therefore, it can be said that the vector orthogonal to the given vectors ( 3 11 ) ∧ ( −12 1 ) is
u=( −1
√ 66 , −4
√66 , 7
√66 )
Further, it is essential to note that the negative of the orthogonal vector is also termed as
orthogonal. Hence, −u=( 1
√ 66 , 4
√ 66 , −7
√ 66 ) is also termed as orthogonal vector.
Finally, the two vectors orthogonal to ( 3 11 )∧ (−12 1 ) are shown below:
u=
( −1
√ 66 , −4
√66 , 7
√66 )
−u=
( 1
√66 , 4
√ 66 , −7
√66 )
15

Question 10
Volume of parallelepiped spanned by vector =?
u=¿ 1,0,4>¿
v=¿ 1,3,1>¿
w=← 4,2,6>¿
16

It can be seen from the above figure that vector u and v are perpendicular to each other. Hence,
u × v=¿ 1,0,4>×<1,3,1>¿
Rule of cross product of the two vectors
¿ ( 0.1−4.3 4.1−1.11.3−0.1 )
¿( 0−12 4−1 3−0)
u × v= ( −12 3 3 )
Now,
Find dot product of u × v withvector w
( u × v ) . w= (−12 3 3 ) . (−4 2 6 )
Rule of dot product of the two vectors
¿ (−12 ) . (−4 )+ ( 3.2 )+ ( 3.6 )
¿ 48+ 6+18
¿ 72
17

Hence, the volume of parallelepiped spanned by vector is 72.
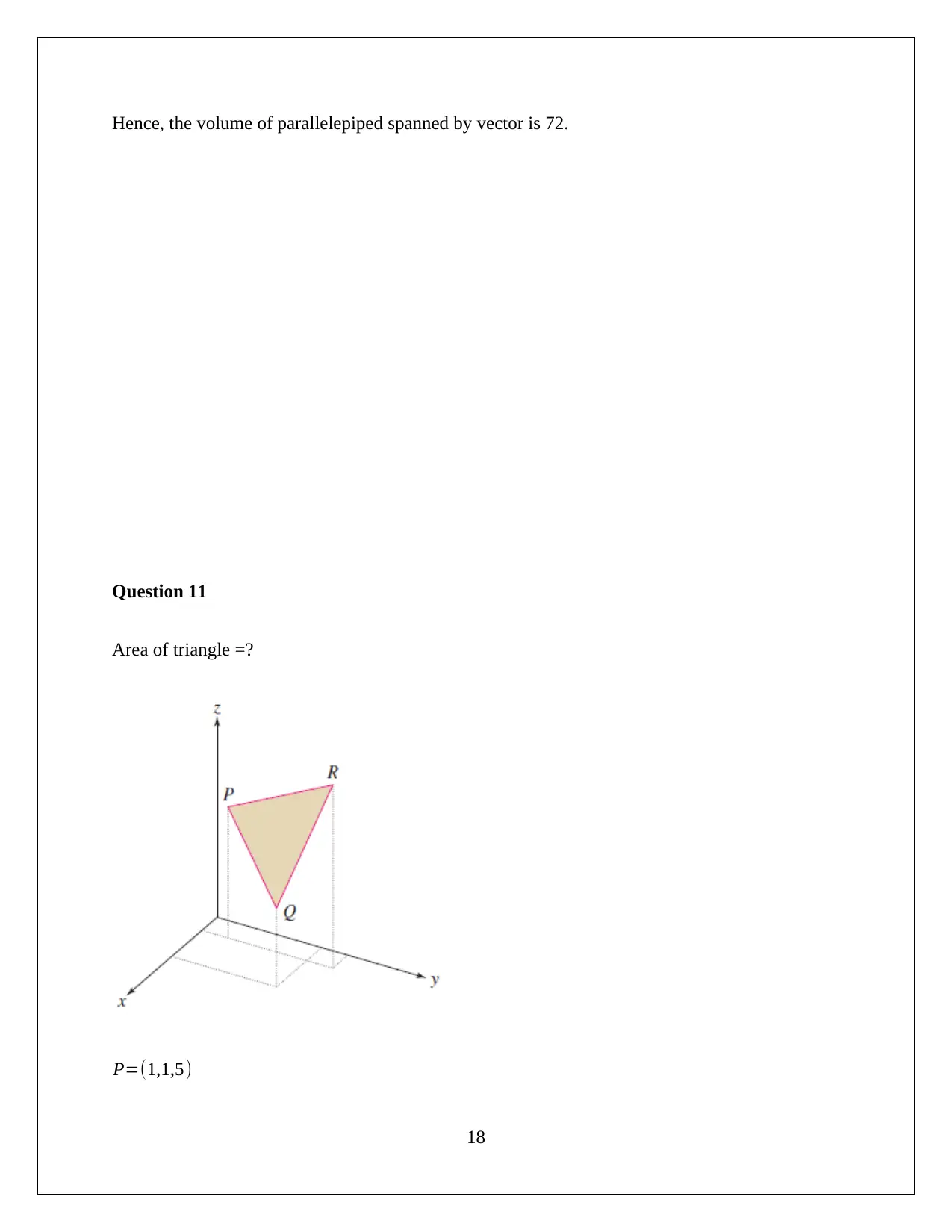
Question 11
Area of triangle =?
P=(1,1,5)
18

Q= ( 3 , 4,3 )
R=(1,5,7)
Needs to find PQ and PR from the above values
Let
Compute PQ∧PR
P Q= ( 3−1 , 4−1, 3−5 ) =(2 ,3 ,−2)
PR= ( 1−3 ,5−4 ,7−3 ) =(−2, 1 , 4)
Area of triangle would be determined as shown below:
∆= 1
2 ∨PQ × PR∨¿
PQ × PR=(2, 3 ,−2) ×(−2 ,1 , 4)
Rule of cross product of the two vectors
¿ ( 3.4− (−2 ) .1 (−2 ) .(−2)−2.4 2.1−3.(−2) )
¿ ( 12+2 4−8 2+6 )
¿ ( 14−4 8 )
19

Now,
|PQ × PR|= √ ( 14 ) 2+ ( −4 ) 2+ ( 8 ) 2= √ 276=16.61
∆= 1
2 |PQ × PR|= 1
2 ×16.61=8.306
Hence, area of triangle is 8.306.
Question 12
Equation of the plane in scalar form =?
With normal vector n=
(−
2
4
1 )
Passing through the point ( 1
3 , 2
3 , 1 )
Let the P is the point passes through, R which is an arbitrary point (x, y, z) on the plane.
n . ( R−P )
20

(−
2
4
1 ) . ( x− 1
3 , y− 2
3 , z−1 )=0
(−
2
4
1 ) ( 3 x−1
3 , 3 y −2
3 , z−1 )=0
2. ( 3 x−1
3 )−4 (3 y −2
3 )+1 ( z −1 )=0
6 x−2
3 +−12 y+8
3 + z−1=0
6 x−2−12 y +8+ 3 z−3=0
6 x−12 y +3 z+3=0
Hence the equation of plane in the form of ax +by +cz =d is shown below:
6 x−12 y +3 z=−3
Question 13
Equation of plane passing through three points =?
P= (5,1 , 1 ), Q= (1,1,2 ), R= ( 2,1,1 )
PQ=Q−P= ( 1−5 1−1 2−1 ) = ( −4 , 0 ,1 )
PR=R−P= ( 2−5 1−11−1 ) =(−3 , 0 , 0)
21

Both PQ and PR lie in the plane and therefore, their cross product i.e. PQ× PRis orthogonal to
the plane and hence, it can be said that it is a normal vector.
PQ × PR= (−4 , 0 ,1 ) × (−3 ,0 , 0 )
Rule of cross product of the two vectors
¿ ¿
¿ ( 0−0−3−0−0−0 )
n=PQ × PR=(0−3 0)
Point P= ( 5,1 , 1 ) and normal vector n, would be used to find the equation of plane.
0 ( x−5 ) −3 ( y−1 ) +0 ( z−1 ) =0
−3 y +3=0
Hence, the equation of plane would be 0x-3y +0z +3 = 0
Question 14
Equation of plane =?
Plane is passing through the point ¿(4 , 1 , 9)
Plane is parallel to x + y + z=3
22

The normal vector to the plane (which is || to the plane) would be determined as highlighted
below:
n= ( 1,1,1 )
The equation of plane which is passing through the point (x0 , y0 , z0) and is having direction ratio
of normal vector (A, B, C) is shown below:
A ( x−x0 ) + B ( y− y0 ) +C ( z−z0 )=0…….(1)
In present case ( A , B , C )=Normal vector= (1,1,1 ) (x0 , y0 , z0) = Plane is passing through the
point ¿(4,1,9)
Equation (1) A ( x−x0 ) + B ( y− y0 ) +C ( z−z0 )=0
1 ( x−4 ) +1 ( y −1 ) +1 ( z−9 )=0
x−4+ y −1+ z−9=0
x + y + z−14=0
x + y + z=−14
Equation of plane x + y + z=14
Question 15
Equation of the plane =?
Given line equations
23

r1 ( t ) =
( t
2t
3 t )
r2 ( t ) =
( 3t
t
8t )
 Cross product of the line equations (Normal vector)
r1 ( t ) ×r 2 ( t ) =
( t
2t
3 t ) × ( 3t
t
8t )
o r
r1 ( t ) ×r 2 ( t ) = ( 1 23 ) × ( 3 1 8 )
Rule of cross product of the two vectors
r1 ( t ) ×r 2 ( t ) = ( 2.8−3.13.3−1.8 1.1−2.3 )
r1 ( t ) ×r 2 ( t ) = ( 13 1−5 )
 Point of plane would be computed as
¿ ( 2 ,1 , 0 )
24

Equation of plane
13 ( x−2 ) +1 ( y−1 ) −5 ( z−0 ) =0
13 x+ y−5 z=27
25

Question 16
Let
 Plane 1 :2 x−4 y−z=3Or 2 x−4 y−z−3=0
Compare with a1 x+ b1 y+ c1 z +d1=0
a1=2 ,b1=−4 , c1=−1 , d1 =−3
 Plane 2 :−6 x+ 12 y +3 z=1Or −6 x +12 y +3 z−1=0
Compare with a2 x +b2 y+ c2 z +d2=0
a2=−6 , b2=12 , c2=3 , d2=−1
These two planes would be termed as parallel to each other only when the below highlighted
condition is satisfied.
a1
a2
= b1
b2
= c1
c2
2
−6 =−4
12 =−1
3
Simplification
−1
3 =−1
3 =−1
3
The condition is satisfied and thus, the given planes are parallel.
26

27

28

29

30