CFCC Capital Budgeting: Simulation Analysis, NPV, and IRR Analysis
VerifiedAdded on 2021/12/09
|9
|1773
|42
Project
AI Summary
This assignment analyzes a capital budgeting project for CFCC using various financial techniques including WACC, NPV, IRR, MIRR, payback period, and ARR. The analysis evaluates the project's performance under different economic scenarios (recession, slow growth, strong growth) and recommends acceptance or rejection based on profitability metrics. Sensitivity analysis explores the impact of changes in sales units and salvage value on NPV. A Monte Carlo simulation is performed to assess project risk, considering factors like unit sales, price, and costs. The analysis concludes with recommendations on project acceptance, risk adjustment, and financial decision-making based on the simulation results. The project also includes the option to abandon the project and its impact on the NPV.

RUNNING HEAD: CAPITAL BUDGETING
SImulation analysis
Capital budgeting
Monte Carlo
Name of the author-
University Name-
SImulation analysis
Capital budgeting
Monte Carlo
Name of the author-
University Name-
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Capital budgeting 2
Table of Contents
References.................................................................................................................................................12
Table of Contents
References.................................................................................................................................................12

Capital budgeting 3
Answer to question no-1
Weighted average cost of
capital
Particulars Amount
Weights
(A)
Cost of capital
(B) A*B
Equity
$
5,000,000.00
0.5
9 15.25% 8.97%
Debt
$
3,500,000.00
0.4
1 6.82% 2.81%
Total
$
8,500,000.00
1.0
0
11.78
%
The WACC of CFCC is calculated at 11.78% by considering the calculated cost of equity and
after tax cost of debt (Dornheim, et al. 2016).
Answer to question no- 2
The payback period, NPV, IRR, MIRR and ARR are the capital budgeting techniques that are
used to evaluate an investment proposal from different perspectives.
In case of CFCC, if economy is in state of recession then the project of new assembly will give
following outcome (Dewachter, et al. 2015).
NPV ($312,646.32)
IRR -1.74%
MIRR 4%
PI $ 0.73
ARR $ 0.08
PBP More than 5 years
When economy is in slow growth state:
NPV $31,017.55
IRR 12.88%
MIRR 12%
PI $ 1.03
ARR $ 0.18
PBP 4.16 years
When economy is in strong growth state:
Answer to question no-1
Weighted average cost of
capital
Particulars Amount
Weights
(A)
Cost of capital
(B) A*B
Equity
$
5,000,000.00
0.5
9 15.25% 8.97%
Debt
$
3,500,000.00
0.4
1 6.82% 2.81%
Total
$
8,500,000.00
1.0
0
11.78
%
The WACC of CFCC is calculated at 11.78% by considering the calculated cost of equity and
after tax cost of debt (Dornheim, et al. 2016).
Answer to question no- 2
The payback period, NPV, IRR, MIRR and ARR are the capital budgeting techniques that are
used to evaluate an investment proposal from different perspectives.
In case of CFCC, if economy is in state of recession then the project of new assembly will give
following outcome (Dewachter, et al. 2015).
NPV ($312,646.32)
IRR -1.74%
MIRR 4%
PI $ 0.73
ARR $ 0.08
PBP More than 5 years
When economy is in slow growth state:
NPV $31,017.55
IRR 12.88%
MIRR 12%
PI $ 1.03
ARR $ 0.18
PBP 4.16 years
When economy is in strong growth state:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Capital budgeting 4
NPV $477,216.57
IRR 25.90%
MIRR 21%
PI $ 1.42
ARR $ 0.23
PBP 3.54 years
Recommendation
It can be observed that in state of recession, the project will not be profitable as it has negative
NPV and IRR. Furthermore, the payback period is also more than the economic life of the
project (Bernal, et al. 2015). )However, the situation got reverse when the economy has slow
growth and strong growth as the proposal become profitable and also the IRR is more than the
WACC of the company. Moreover the payback period is less than the economic life. Thus, it is
recommended to accept the project when the economy is in the state of slow and strong growth
and the same should be avoided in case of recession (Kou, Peng, & Wang, 2014).
Answer to question no-3
Value of the option to abandon the project
If the project is abandon in year
2001
Expected life 1
Cash outflow $ 1,140,000.00
Total cash inflow $ 1,099,244.00
Discounting rate 11.78%
Pave of cash inflow $ 983,409.8851
Pave of cash outflow $ 1,140,000.00
Net present value $ (156,590.11)
If the economy is in slow and strong growth and project is taken over 5
years
NPV (slow growth) $31,017.55
NPV (Strong growth) $477,216.57
NPV (recession) ($312,646.32)
In the situation of recession, if the project is abandoned in year 2001, making its expected life to
be 1 year, the expected NPV will be -$156,590.11. However, if the project is continued for the
long five years in the same situation then its NPV will be -$312,646.32 (Rubinstein, & Kroese,
2016). In both the situations, it is not profitable and hence recommended to adopt the option of
NPV $477,216.57
IRR 25.90%
MIRR 21%
PI $ 1.42
ARR $ 0.23
PBP 3.54 years
Recommendation
It can be observed that in state of recession, the project will not be profitable as it has negative
NPV and IRR. Furthermore, the payback period is also more than the economic life of the
project (Bernal, et al. 2015). )However, the situation got reverse when the economy has slow
growth and strong growth as the proposal become profitable and also the IRR is more than the
WACC of the company. Moreover the payback period is less than the economic life. Thus, it is
recommended to accept the project when the economy is in the state of slow and strong growth
and the same should be avoided in case of recession (Kou, Peng, & Wang, 2014).
Answer to question no-3
Value of the option to abandon the project
If the project is abandon in year
2001
Expected life 1
Cash outflow $ 1,140,000.00
Total cash inflow $ 1,099,244.00
Discounting rate 11.78%
Pave of cash inflow $ 983,409.8851
Pave of cash outflow $ 1,140,000.00
Net present value $ (156,590.11)
If the economy is in slow and strong growth and project is taken over 5
years
NPV (slow growth) $31,017.55
NPV (Strong growth) $477,216.57
NPV (recession) ($312,646.32)
In the situation of recession, if the project is abandoned in year 2001, making its expected life to
be 1 year, the expected NPV will be -$156,590.11. However, if the project is continued for the
long five years in the same situation then its NPV will be -$312,646.32 (Rubinstein, & Kroese,
2016). In both the situations, it is not profitable and hence recommended to adopt the option of
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Capital budgeting 5
abandoning the same in the very first year. In slow and strong growth state, the net present
values are positive and high making the project profitable and is continued over the five years
(Chu, et al. 2017).
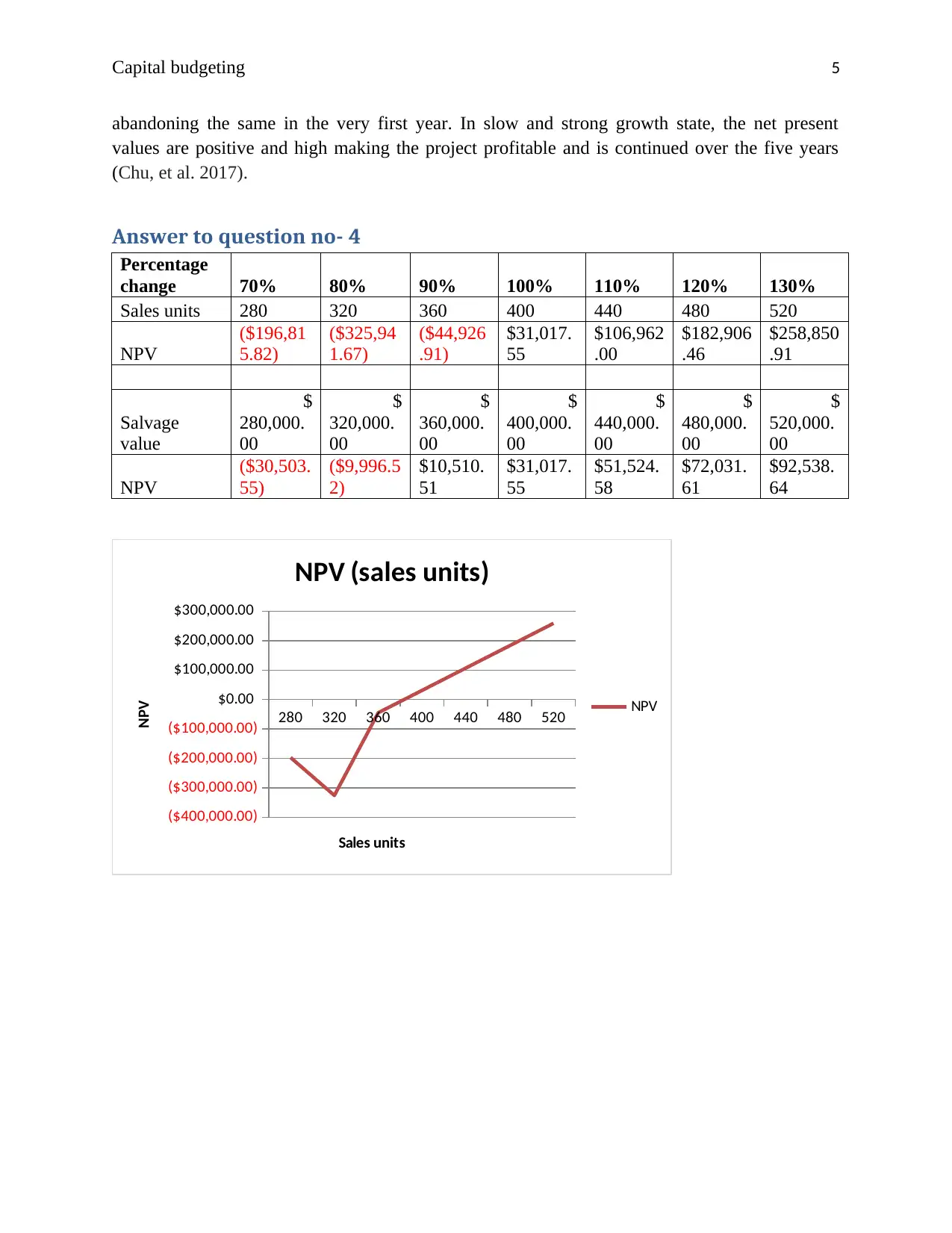
Answer to question no- 4
Percentage
change 70% 80% 90% 100% 110% 120% 130%
Sales units 280 320 360 400 440 480 520
NPV
($196,81
5.82)
($325,94
1.67)
($44,926
.91)
$31,017.
55
$106,962
.00
$182,906
.46
$258,850
.91
Salvage
value
$
280,000.
00
$
320,000.
00
$
360,000.
00
$
400,000.
00
$
440,000.
00
$
480,000.
00
$
520,000.
00
NPV
($30,503.
55)
($9,996.5
2)
$10,510.
51
$31,017.
55
$51,524.
58
$72,031.
61
$92,538.
64
280 320 360 400 440 480 520
($400,000.00)
($300,000.00)
($200,000.00)
($100,000.00)
$0.00
$100,000.00
$200,000.00
$300,000.00
NPV (sales units)
NPV
Sales units
NPV
abandoning the same in the very first year. In slow and strong growth state, the net present
values are positive and high making the project profitable and is continued over the five years
(Chu, et al. 2017).
Answer to question no- 4
Percentage
change 70% 80% 90% 100% 110% 120% 130%
Sales units 280 320 360 400 440 480 520
NPV
($196,81
5.82)
($325,94
1.67)
($44,926
.91)
$31,017.
55
$106,962
.00
$182,906
.46
$258,850
.91
Salvage
value
$
280,000.
00
$
320,000.
00
$
360,000.
00
$
400,000.
00
$
440,000.
00
$
480,000.
00
$
520,000.
00
NPV
($30,503.
55)
($9,996.5
2)
$10,510.
51
$31,017.
55
$51,524.
58
$72,031.
61
$92,538.
64
280 320 360 400 440 480 520
($400,000.00)
($300,000.00)
($200,000.00)
($100,000.00)
$0.00
$100,000.00
$200,000.00
$300,000.00
NPV (sales units)
NPV
Sales units
NPV
Capital budgeting 6
$280,000.00
$320,000.00
$360,000.00
$400,000.00
$440,000.00
$480,000.00
$520,000.00
($40,000.00)
($20,000.00)
$0.00
$20,000.00
$40,000.00
$60,000.00
$80,000.00
$100,000.00
NPV(salvage value)
NPV
Salvage value
NPV
The sensitivity analysis has been performed to in order to enhance the evaluation of the project.
Under this, keeping the salvage value same, the changes are been made in the unit sales of the
project. Later the percentage changes are made in the salvage value, keeping the units same over
the five years. It can be interpreted from the outcomes that when the units are changed, the
project has reported a negative NPV in the case of 70%, 80% and 90%. After that the NPV
turned out to be positive when the units got increased by 100%, 110%, 120% and 130%. This
indicated that if the company produces units at less than 100% level, the project will make losses
and is not profitable (Kurzke, & Halliwell, 2018).
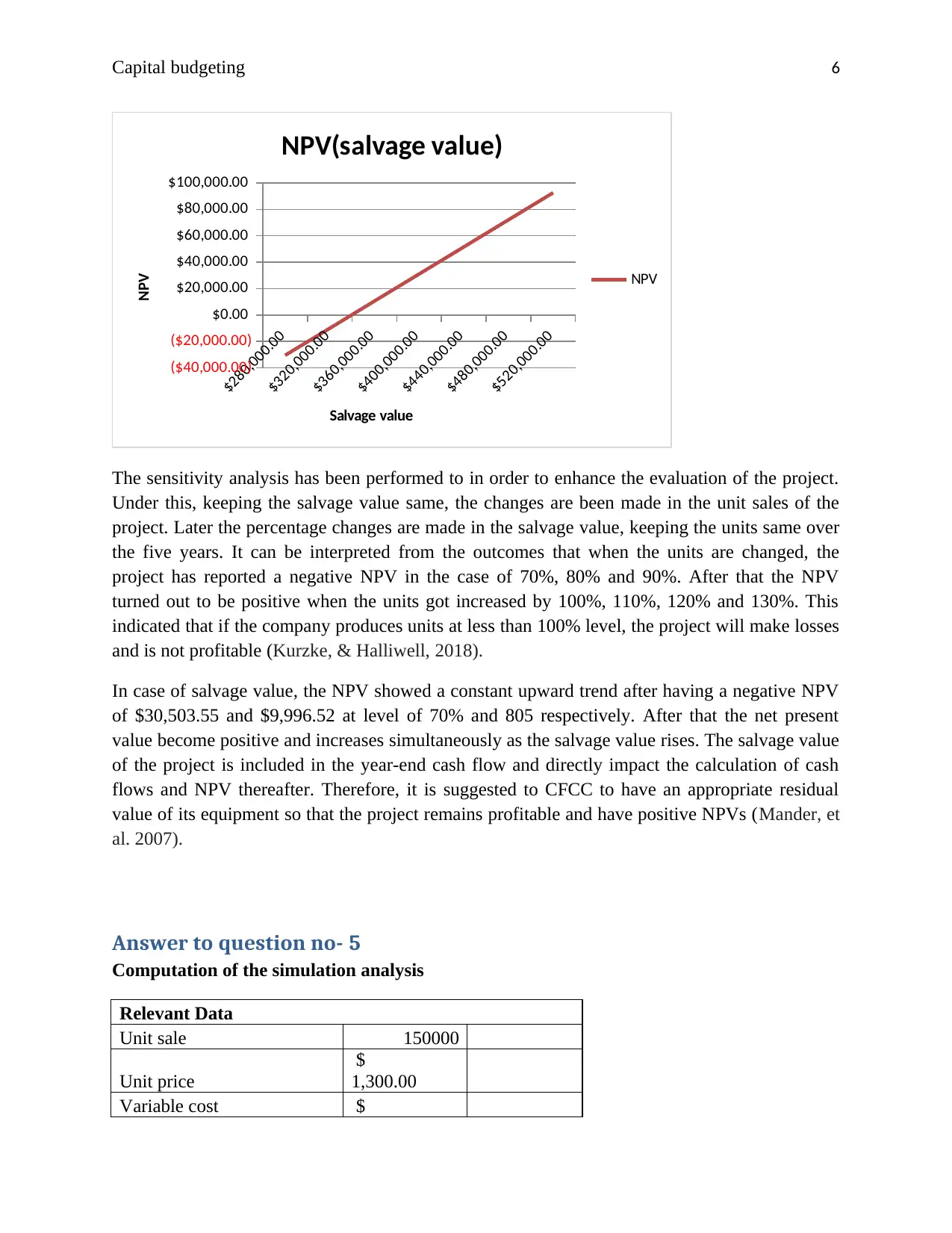
In case of salvage value, the NPV showed a constant upward trend after having a negative NPV
of $30,503.55 and $9,996.52 at level of 70% and 805 respectively. After that the net present
value become positive and increases simultaneously as the salvage value rises. The salvage value
of the project is included in the year-end cash flow and directly impact the calculation of cash
flows and NPV thereafter. Therefore, it is suggested to CFCC to have an appropriate residual
value of its equipment so that the project remains profitable and have positive NPVs (Mander, et
al. 2007).
Answer to question no- 5
Computation of the simulation analysis
Relevant Data
Unit sale 150000
Unit price
$
1,300.00
Variable cost $
$280,000.00
$320,000.00
$360,000.00
$400,000.00
$440,000.00
$480,000.00
$520,000.00
($40,000.00)
($20,000.00)
$0.00
$20,000.00
$40,000.00
$60,000.00
$80,000.00
$100,000.00
NPV(salvage value)
NPV
Salvage value
NPV
The sensitivity analysis has been performed to in order to enhance the evaluation of the project.
Under this, keeping the salvage value same, the changes are been made in the unit sales of the
project. Later the percentage changes are made in the salvage value, keeping the units same over
the five years. It can be interpreted from the outcomes that when the units are changed, the
project has reported a negative NPV in the case of 70%, 80% and 90%. After that the NPV
turned out to be positive when the units got increased by 100%, 110%, 120% and 130%. This
indicated that if the company produces units at less than 100% level, the project will make losses
and is not profitable (Kurzke, & Halliwell, 2018).
In case of salvage value, the NPV showed a constant upward trend after having a negative NPV
of $30,503.55 and $9,996.52 at level of 70% and 805 respectively. After that the net present
value become positive and increases simultaneously as the salvage value rises. The salvage value
of the project is included in the year-end cash flow and directly impact the calculation of cash
flows and NPV thereafter. Therefore, it is suggested to CFCC to have an appropriate residual
value of its equipment so that the project remains profitable and have positive NPVs (Mander, et
al. 2007).
Answer to question no- 5
Computation of the simulation analysis
Relevant Data
Unit sale 150000
Unit price
$
1,300.00
Variable cost $
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Capital budgeting 7
1,035.00
Cash operating fixed cost
$
34.40 Million
Lease payments
$
0.64 Million
Equipment cost
$
16.90 Million
Depreciation
Salvage value
$
3.00 Million
Working capital
$
5.90 Million
Tax rate 43%
WACC 15%
Price inflation 3%
Variable cost and cash fixed
cost inflation 2%
There will be negative NPV in this case as the project is already giving way more higher
negative Net present value out of its invested capital.
Particular $ millions
Mean (312,646.32)
Maximum value (312,646.32)
Minimum value (312,646.32)
Standard deviation 1.00
Co-efficient of
variation (0.00)
It is analyzed that Standards deviation in the NPV would be 1 as there is no change in the NPV
in all the trials of the simulations. Therefore, Co-efficient of the variation will also be zero
(Berne, & Schramm, 2016).
(For simulation trials and error please check the Excel file attached)
(Please check the excel)
1,035.00
Cash operating fixed cost
$
34.40 Million
Lease payments
$
0.64 Million
Equipment cost
$
16.90 Million
Depreciation
Salvage value
$
3.00 Million
Working capital
$
5.90 Million
Tax rate 43%
WACC 15%
Price inflation 3%
Variable cost and cash fixed
cost inflation 2%
There will be negative NPV in this case as the project is already giving way more higher
negative Net present value out of its invested capital.
Particular $ millions
Mean (312,646.32)
Maximum value (312,646.32)
Minimum value (312,646.32)
Standard deviation 1.00
Co-efficient of
variation (0.00)
It is analyzed that Standards deviation in the NPV would be 1 as there is no change in the NPV
in all the trials of the simulations. Therefore, Co-efficient of the variation will also be zero
(Berne, & Schramm, 2016).
(For simulation trials and error please check the Excel file attached)
(Please check the excel)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Capital budgeting 8
Answer to question no-6
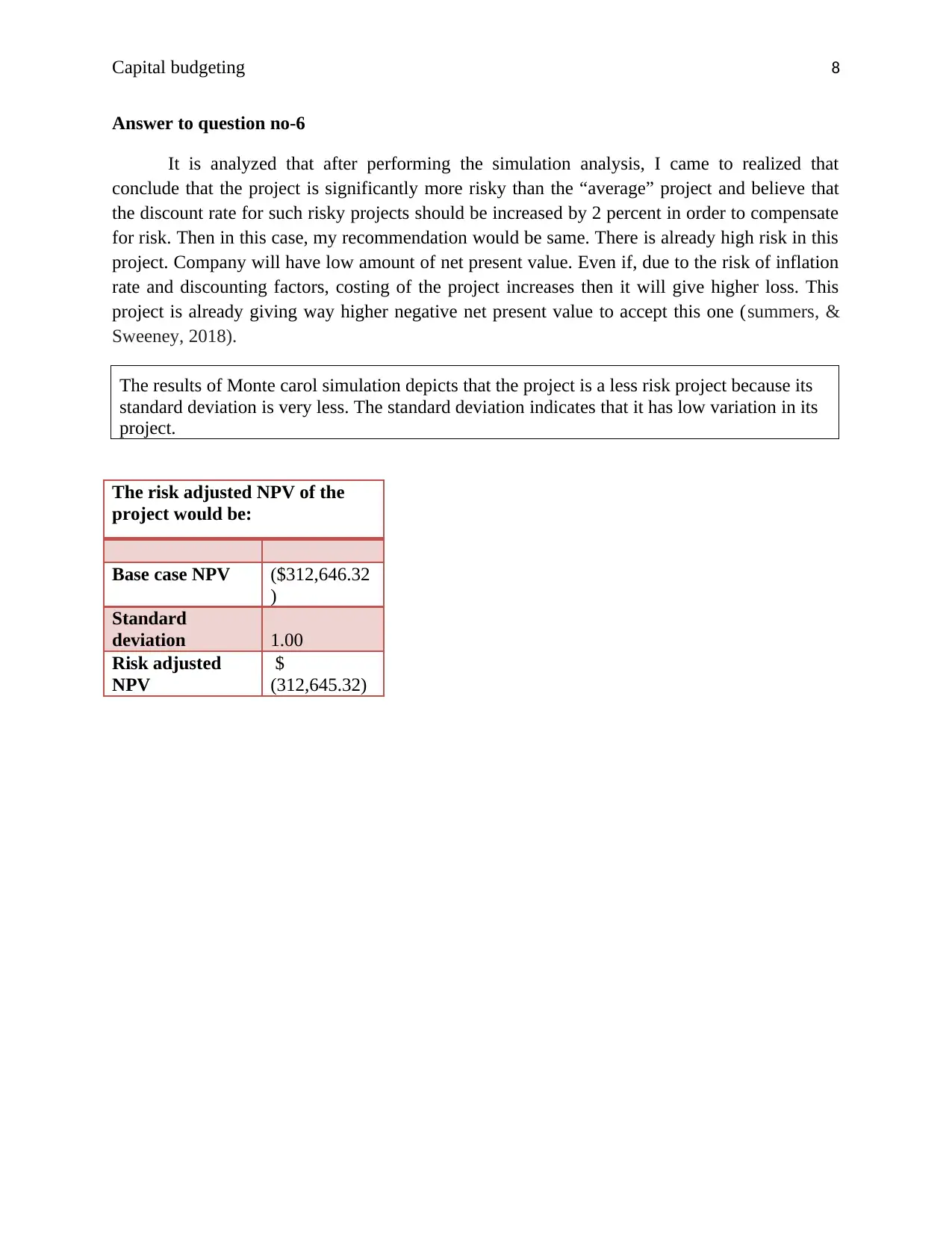
It is analyzed that after performing the simulation analysis, I came to realized that
conclude that the project is significantly more risky than the “average” project and believe that
the discount rate for such risky projects should be increased by 2 percent in order to compensate
for risk. Then in this case, my recommendation would be same. There is already high risk in this
project. Company will have low amount of net present value. Even if, due to the risk of inflation
rate and discounting factors, costing of the project increases then it will give higher loss. This
project is already giving way higher negative net present value to accept this one (summers, &
Sweeney, 2018).
The results of Monte carol simulation depicts that the project is a less risk project because its
standard deviation is very less. The standard deviation indicates that it has low variation in its
project.
The risk adjusted NPV of the
project would be:
Base case NPV ($312,646.32
)
Standard
deviation 1.00
Risk adjusted
NPV
$
(312,645.32)
Answer to question no-6
It is analyzed that after performing the simulation analysis, I came to realized that
conclude that the project is significantly more risky than the “average” project and believe that
the discount rate for such risky projects should be increased by 2 percent in order to compensate
for risk. Then in this case, my recommendation would be same. There is already high risk in this
project. Company will have low amount of net present value. Even if, due to the risk of inflation
rate and discounting factors, costing of the project increases then it will give higher loss. This
project is already giving way higher negative net present value to accept this one (summers, &
Sweeney, 2018).
The results of Monte carol simulation depicts that the project is a less risk project because its
standard deviation is very less. The standard deviation indicates that it has low variation in its
project.
The risk adjusted NPV of the
project would be:
Base case NPV ($312,646.32
)
Standard
deviation 1.00
Risk adjusted
NPV
$
(312,645.32)

Capital budgeting 9
References
Bernal, M. A., Bordage, M. C., Brown, J. M. C., Davídková, M., Delage, E., El Bitar, Z., ... &
Karamitros, M. (2015). Track structure modeling in liquid water: A review of the Geant4-
DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Physica
Medica, 31(8), 861-874.
Berne, R., & Schramm, R. (2016). The financial analysis of governments. Englewood Cliffs, NJ:
Prentice-Hall.
Chu, P. L., Vanderghem, C., MacLean, H. L., & Saville, B. A. (2017). Financial analysis and
risk assessment of hydroprocessed renewable jet fuel production from camelina, carinata
and used cooking oil. Applied energy, 198,(1) 401-409.
Dewachter, H., Iania, L., Lyrio, M., & de Sola Perea, M. (2015). A macro-financial analysis of
the euro area sovereign bond market. Journal of Banking & Finance, 50,(3) 308-325.
Dornheim, T., Groth, S., Sjostrom, T., Malone, F. D., Foulkes, W. M. C., & Bonitz, M. (2016).
Ab initio quantum Monte Carlo simulation of the warm dense electron gas in the
thermodynamic limit. Physical review letters, 117(15), 156403.
Kou, G., Peng, Y., & Wang, G. (2014). Evaluation of clustering algorithms for financial risk
analysis using MCDM methods. Information Sciences, 275, (1)1-12.
Kurzke, J., & Halliwell, I. (2018). Monte Carlo Simulations. In Propulsion and Power (pp. 723-
738). Australia: Springer, Cham.
Mander, J. B., Dhakal, R. P., Mashiko, N., & Solberg, K. M. (2007). Incremental dynamic
analysis applied to seismic financial risk assessment of bridges. Engineering
structures, 29(10), 2662-2672.
Rubinstein, R. Y., & Kroese, D. P. (2016). Simulation and the Monte Carlo method (Vol. 10).
Australia: John Wiley & Sons.
Summers, S. L., & Sweeney, J. T. (2018). Fraudulently misstated financial statements and
insider trading: An empirical analysis. Accounting Review,2(1) 131-146.
References
Bernal, M. A., Bordage, M. C., Brown, J. M. C., Davídková, M., Delage, E., El Bitar, Z., ... &
Karamitros, M. (2015). Track structure modeling in liquid water: A review of the Geant4-
DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Physica
Medica, 31(8), 861-874.
Berne, R., & Schramm, R. (2016). The financial analysis of governments. Englewood Cliffs, NJ:
Prentice-Hall.
Chu, P. L., Vanderghem, C., MacLean, H. L., & Saville, B. A. (2017). Financial analysis and
risk assessment of hydroprocessed renewable jet fuel production from camelina, carinata
and used cooking oil. Applied energy, 198,(1) 401-409.
Dewachter, H., Iania, L., Lyrio, M., & de Sola Perea, M. (2015). A macro-financial analysis of
the euro area sovereign bond market. Journal of Banking & Finance, 50,(3) 308-325.
Dornheim, T., Groth, S., Sjostrom, T., Malone, F. D., Foulkes, W. M. C., & Bonitz, M. (2016).
Ab initio quantum Monte Carlo simulation of the warm dense electron gas in the
thermodynamic limit. Physical review letters, 117(15), 156403.
Kou, G., Peng, Y., & Wang, G. (2014). Evaluation of clustering algorithms for financial risk
analysis using MCDM methods. Information Sciences, 275, (1)1-12.
Kurzke, J., & Halliwell, I. (2018). Monte Carlo Simulations. In Propulsion and Power (pp. 723-
738). Australia: Springer, Cham.
Mander, J. B., Dhakal, R. P., Mashiko, N., & Solberg, K. M. (2007). Incremental dynamic
analysis applied to seismic financial risk assessment of bridges. Engineering
structures, 29(10), 2662-2672.
Rubinstein, R. Y., & Kroese, D. P. (2016). Simulation and the Monte Carlo method (Vol. 10).
Australia: John Wiley & Sons.
Summers, S. L., & Sweeney, J. T. (2018). Fraudulently misstated financial statements and
insider trading: An empirical analysis. Accounting Review,2(1) 131-146.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



