Corporate Finance: Project Evaluation and Capital Budgeting Analysis

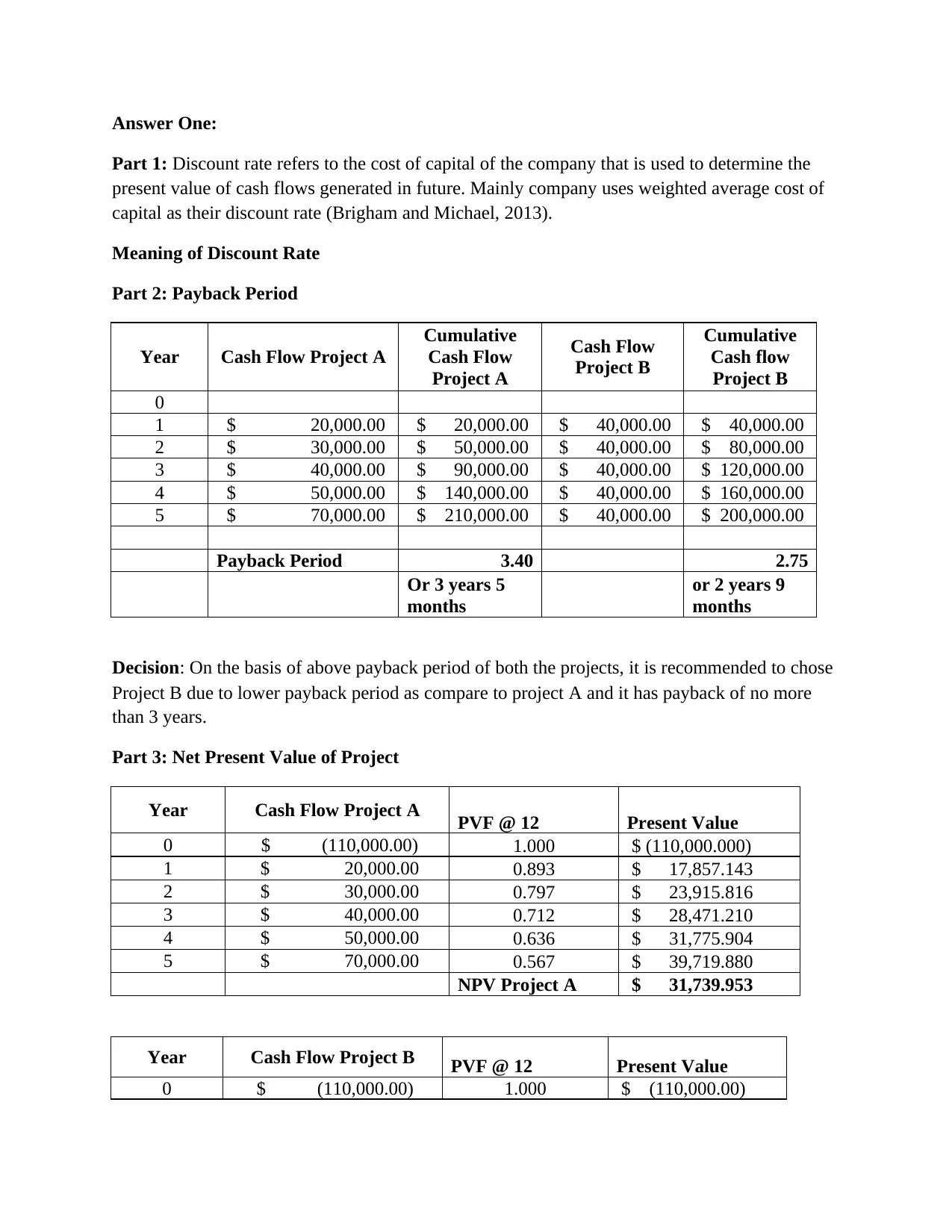
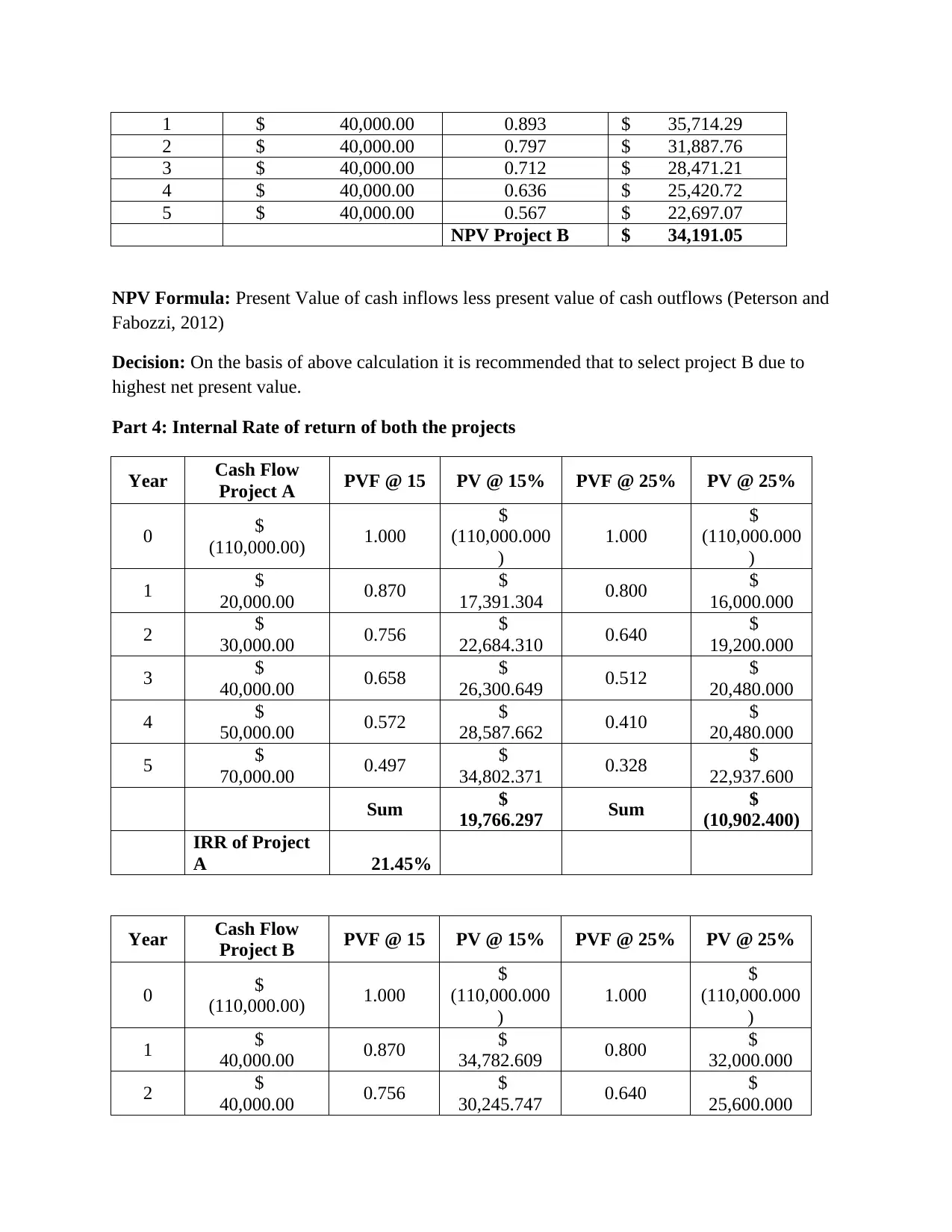
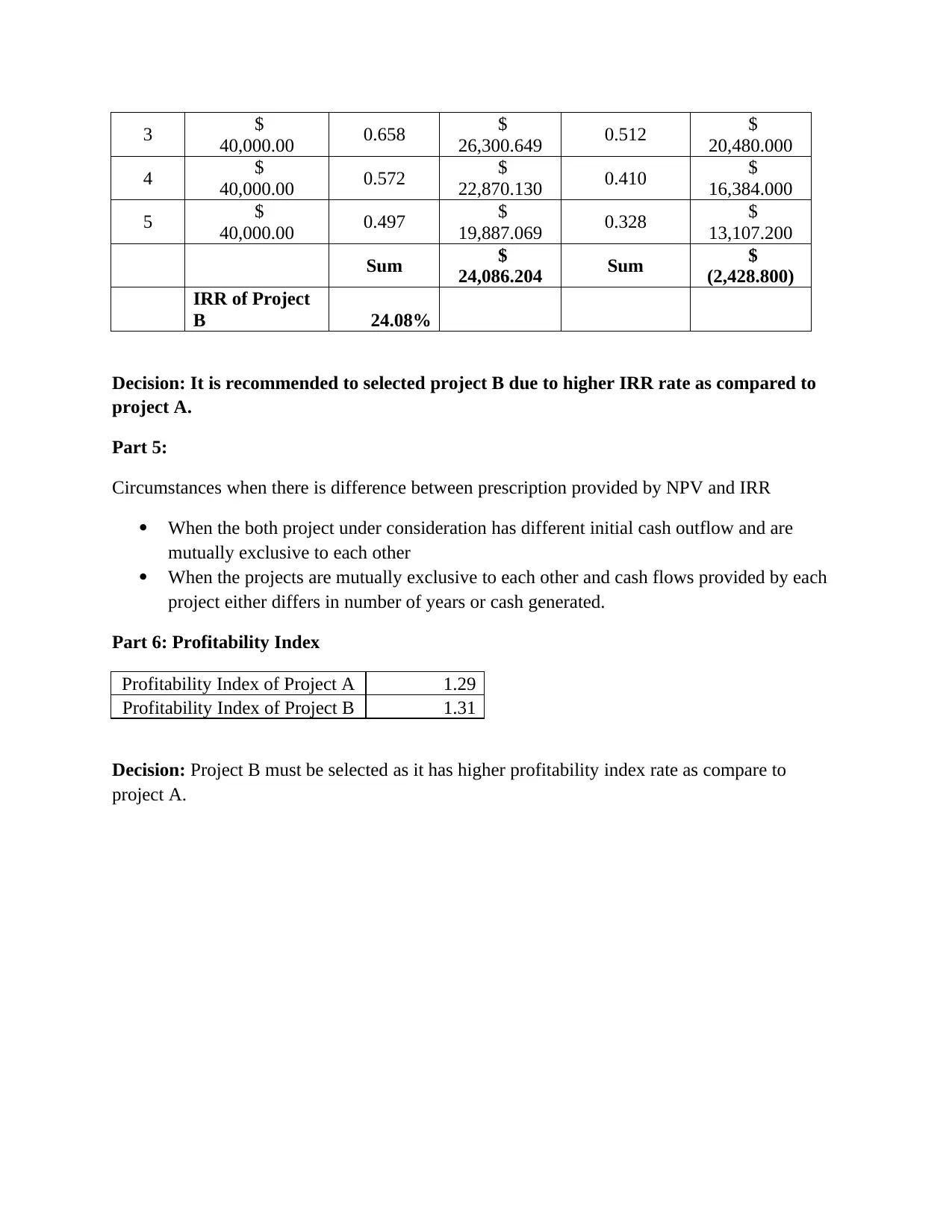
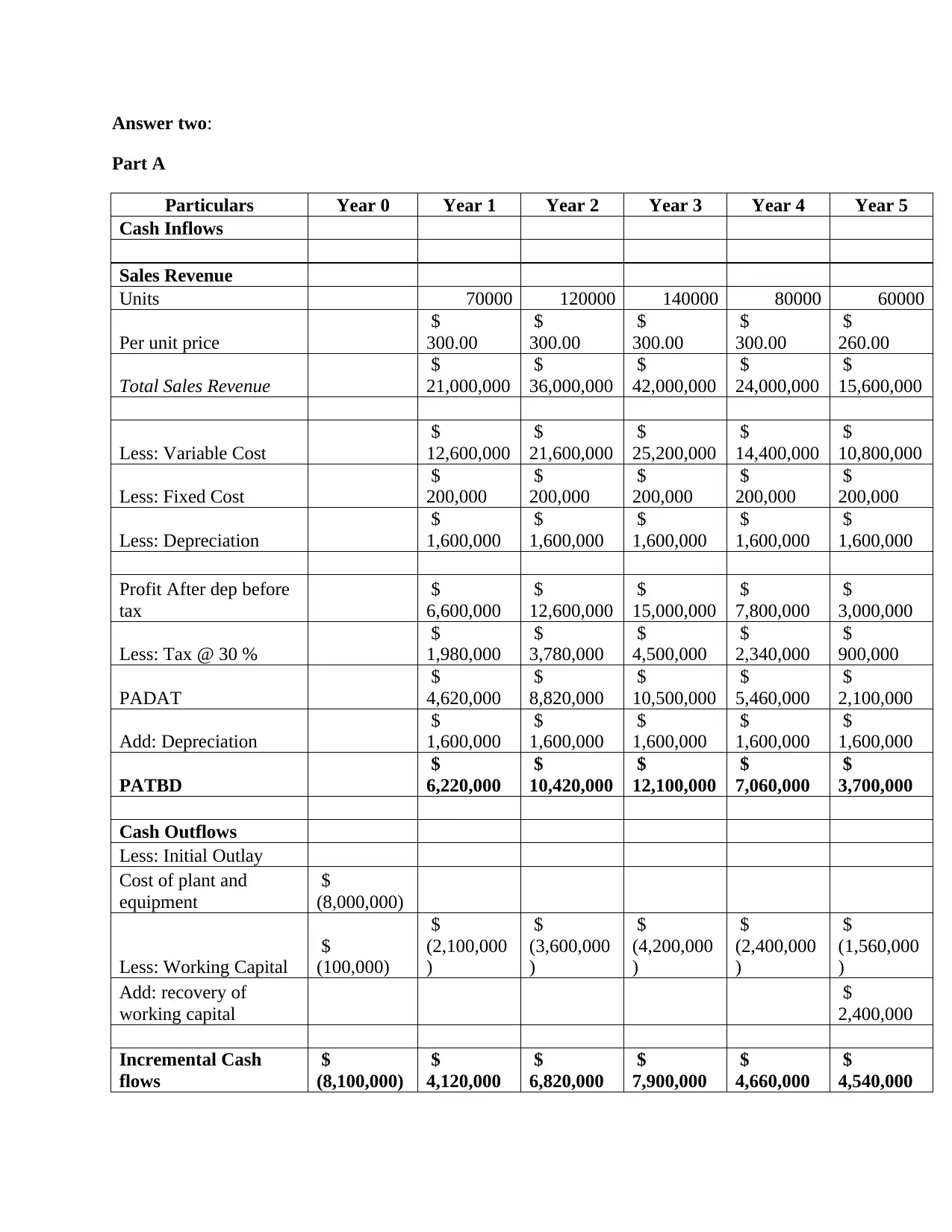
This finance assignment solution delves into project evaluation techniques, providing a comprehensive analysis of two projects using various financial metrics. The assignment starts by defining and explaining the significance of discount rates, including the weighted average cost of capital. It then proceeds to evaluate projects using the payback period method, recommending a project based on its shorter payback time. The core of the assignment focuses on net present value (NPV) and internal rate of return (IRR) calculations, comparing the profitability of two projects and recommending the selection of the project with the higher NPV and IRR. The assignment also discusses circumstances where NPV and IRR prescriptions differ. Furthermore, the solution calculates and interprets the profitability index (PI) to aid in project selection. The second part of the assignment involves a detailed cash flow analysis for a new project, including incremental cash flow calculations, NPV, and IRR under different discount rates, culminating in a recommendation on whether to accept the project based on the financial analysis. References to academic sources are included to support the analysis.

Answer One:
Part 1: Discount rate refers to the cost of capital of the company that is used to determine the
present value of cash flows generated in future. Mainly company uses weighted average cost of
capital as their discount rate (Brigham and Michael, 2013).
Meaning of Discount Rate
Part 2: Payback Period
Year Cash Flow Project A
Cumulative
Cash Flow
Project A
Cash Flow
Project B
Cumulative
Cash flow
Project B
0
1 $ 20,000.00 $ 20,000.00 $ 40,000.00 $ 40,000.00
2 $ 30,000.00 $ 50,000.00 $ 40,000.00 $ 80,000.00
3 $ 40,000.00 $ 90,000.00 $ 40,000.00 $ 120,000.00
4 $ 50,000.00 $ 140,000.00 $ 40,000.00 $ 160,000.00
5 $ 70,000.00 $ 210,000.00 $ 40,000.00 $ 200,000.00
Payback Period 3.40 2.75
Or 3 years 5
months
or 2 years 9
months
Decision: On the basis of above payback period of both the projects, it is recommended to chose
Project B due to lower payback period as compare to project A and it has payback of no more
than 3 years.
Part 3: Net Present Value of Project
Year Cash Flow Project A PVF @ 12 Present Value
0 $ (110,000.00) 1.000 $ (110,000.000)
1 $ 20,000.00 0.893 $ 17,857.143
2 $ 30,000.00 0.797 $ 23,915.816
3 $ 40,000.00 0.712 $ 28,471.210
4 $ 50,000.00 0.636 $ 31,775.904
5 $ 70,000.00 0.567 $ 39,719.880
NPV Project A $ 31,739.953
Year Cash Flow Project B PVF @ 12 Present Value
0 $ (110,000.00) 1.000 $ (110,000.00)

1 $ 40,000.00 0.893 $ 35,714.29
2 $ 40,000.00 0.797 $ 31,887.76
3 $ 40,000.00 0.712 $ 28,471.21
4 $ 40,000.00 0.636 $ 25,420.72
5 $ 40,000.00 0.567 $ 22,697.07
NPV Project B $ 34,191.05
NPV Formula: Present Value of cash inflows less present value of cash outflows (Peterson and
Fabozzi, 2012)
Decision: On the basis of above calculation it is recommended that to select project B due to
highest net present value.
Part 4: Internal Rate of return of both the projects
Year Cash Flow
Project A PVF @ 15 PV @ 15% PVF @ 25% PV @ 25%
0 $
(110,000.00) 1.000
$
(110,000.000
)
1.000
$
(110,000.000
)
1 $
20,000.00 0.870 $
17,391.304 0.800 $
16,000.000
2 $
30,000.00 0.756 $
22,684.310 0.640 $
19,200.000
3 $
40,000.00 0.658 $
26,300.649 0.512 $
20,480.000
4 $
50,000.00 0.572 $
28,587.662 0.410 $
20,480.000
5 $
70,000.00 0.497 $
34,802.371 0.328 $
22,937.600
Sum $
19,766.297 Sum $
(10,902.400)
IRR of Project
A 21.45%
Year Cash Flow
Project B PVF @ 15 PV @ 15% PVF @ 25% PV @ 25%
0 $
(110,000.00) 1.000
$
(110,000.000
)
1.000
$
(110,000.000
)
1 $
40,000.00 0.870 $
34,782.609 0.800 $
32,000.000
2 $
40,000.00 0.756 $
30,245.747 0.640 $
25,600.000

3 $
40,000.00 0.658 $
26,300.649 0.512 $
20,480.000
4 $
40,000.00 0.572 $
22,870.130 0.410 $
16,384.000
5 $
40,000.00 0.497 $
19,887.069 0.328 $
13,107.200
Sum $
24,086.204 Sum $
(2,428.800)
IRR of Project
B 24.08%
Decision: It is recommended to selected project B due to higher IRR rate as compared to
project A.
Part 5:
Circumstances when there is difference between prescription provided by NPV and IRR
 When the both project under consideration has different initial cash outflow and are
mutually exclusive to each other
 When the projects are mutually exclusive to each other and cash flows provided by each
project either differs in number of years or cash generated.
Part 6: Profitability Index
Profitability Index of Project A 1.29
Profitability Index of Project B 1.31
Decision: Project B must be selected as it has higher profitability index rate as compare to
project A.

Answer two:
Part A
Particulars Year 0 Year 1 Year 2 Year 3 Year 4 Year 5
Cash Inflows
Sales Revenue
Units 70000 120000 140000 80000 60000
Per unit price
$
300.00
$
300.00
$
300.00
$
300.00
$
260.00
Total Sales Revenue
$
21,000,000
$
36,000,000
$
42,000,000
$
24,000,000
$
15,600,000
Less: Variable Cost
$
12,600,000
$
21,600,000
$
25,200,000
$
14,400,000
$
10,800,000
Less: Fixed Cost
$
200,000
$
200,000
$
200,000
$
200,000
$
200,000
Less: Depreciation
$
1,600,000
$
1,600,000
$
1,600,000
$
1,600,000
$
1,600,000
Profit After dep before
tax
$
6,600,000
$
12,600,000
$
15,000,000
$
7,800,000
$
3,000,000
Less: Tax @ 30 %
$
1,980,000
$
3,780,000
$
4,500,000
$
2,340,000
$
900,000
PADAT
$
4,620,000
$
8,820,000
$
10,500,000
$
5,460,000
$
2,100,000
Add: Depreciation
$
1,600,000
$
1,600,000
$
1,600,000
$
1,600,000
$
1,600,000
PATBD
$
6,220,000
$
10,420,000
$
12,100,000
$
7,060,000
$
3,700,000
Cash Outflows
Less: Initial Outlay
Cost of plant and
equipment
$
(8,000,000)
Less: Working Capital
$
(100,000)
$
(2,100,000
)
$
(3,600,000
)
$
(4,200,000
)
$
(2,400,000
)
$
(1,560,000
)
Add: recovery of
working capital
$
2,400,000
Incremental Cash
flows
$
(8,100,000)
$
4,120,000
$
6,820,000
$
7,900,000
$
4,660,000
$
4,540,000

Part B:
Project Initial Outlay
Cost of New plant and Equipment $ 8,000,000
Working Capital $ 100,000
$ 8,100,000
Part C:
Incremental Cash
flows
$
(8,100,000)
$
4,120,000
$
6,820,000
$
7,900,000
$
4,660,000
$
4,540,000
PVF @ 15 1.000 0.870 0.756 0.658 0.572 0.497
Present Value
$
(8,100,000)
$
3,582,609
$
5,156,900
$
5,194,378
$
2,664,370
$
2,257,182
Net Present Value
$
10,755,439
Part D:
Incremental Cash
flows
$
(8,100,000)
$
4,120,000
$
6,820,000
$
7,900,000
$
4,660,000
$
4,540,000
PVF @ 25% 1.000 0.800 0.640 0.512 0.410 0.328
$
(8,100,000)
$
3,296,000
$
4,364,800
$
4,044,800
$
1,908,736
$
1,487,667
NPV
$
7,002,003
Incremental Cash
flows
$
(8,100,000)
$
4,120,000
$
6,820,000
$
7,900,000
$
4,660,000
$
4,540,000
PVF @ 70% 1.000 0.588 0.346 0.204 0.120 0.070
$
(8,100,000)
$
2,423,529
$
2,359,862
$
1,607,979
$
557,944
$
319,751
NPV
$
(830,936)
Internal rate of
Return 65.23%

Part E: Yes, project must be accepted due to positive NPV and higher IRR as compared to cost
of capital i.e. discount rate (Firer, 2012).

References
Brigham, F., and Michael C. 2013. Financial management: Theory & practice. Cengage
Learning.
Firer, C. 2012. Fundamentals of Corporate Finance. McGraw-Hill Company.
Peterson, P,P and Fabozzi,F,J,. 2012. Capital budgeting: theory and practice. John Wiley & sons.