Project: Analyzing Central Tendency Measures and Forecasting
VerifiedAdded on 2023/06/18
|10
|1298
|396
Project
AI Summary
This project report focuses on the analysis of sleeping hour data over ten days using central tendency measures and forecasting methods. The report includes a tabulation of the data, chart representation, and detailed calculations of mean, median, mode, standard deviation, and range. The mean sleeping hours are calculated to be 4.8, while the median is 6. Both 3 and 4 are identified as the mode. Forecasting methods are applied to solve a linear equation and determine the slope, predicting sleeping hours for the 12th and 14th days. The study concludes that numeracy and central tendency measurements are crucial for logical data analysis and evaluation. Desklib offers this project as a solved example for students studying statistics.

PROJECT
1
1
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

TABLE OF CONTENTS
INTRODUCTION...........................................................................................................................2
MAIN BODY..................................................................................................................................2
1. Tabulation of data set...............................................................................................................2
2. Chart representation.................................................................................................................2
3. Discussion and calculation......................................................................................................3
CONCLUSION................................................................................................................................8
REFERENCES................................................................................................................................9
2
INTRODUCTION...........................................................................................................................2
MAIN BODY..................................................................................................................................2
1. Tabulation of data set...............................................................................................................2
2. Chart representation.................................................................................................................2
3. Discussion and calculation......................................................................................................3
CONCLUSION................................................................................................................................8
REFERENCES................................................................................................................................9
2
INTRODUCTION
Numeracy and number based calculations forms part of everyday life and related operations.
In business it is common and mandatory approach to use complete knowledge of analysis and
management of huge data sets (Raza and et.al., 2021). This report provides the understanding
and measurement of central tendency measures of sleeping hour data for ten days. The report
will consist of tabular and chart representation of the data and its analysis using statistical tool
for calculation of central tendency measures. The study also consists of forecasting method for
solving linear equation and to determine the slope of equation.
MAIN BODY
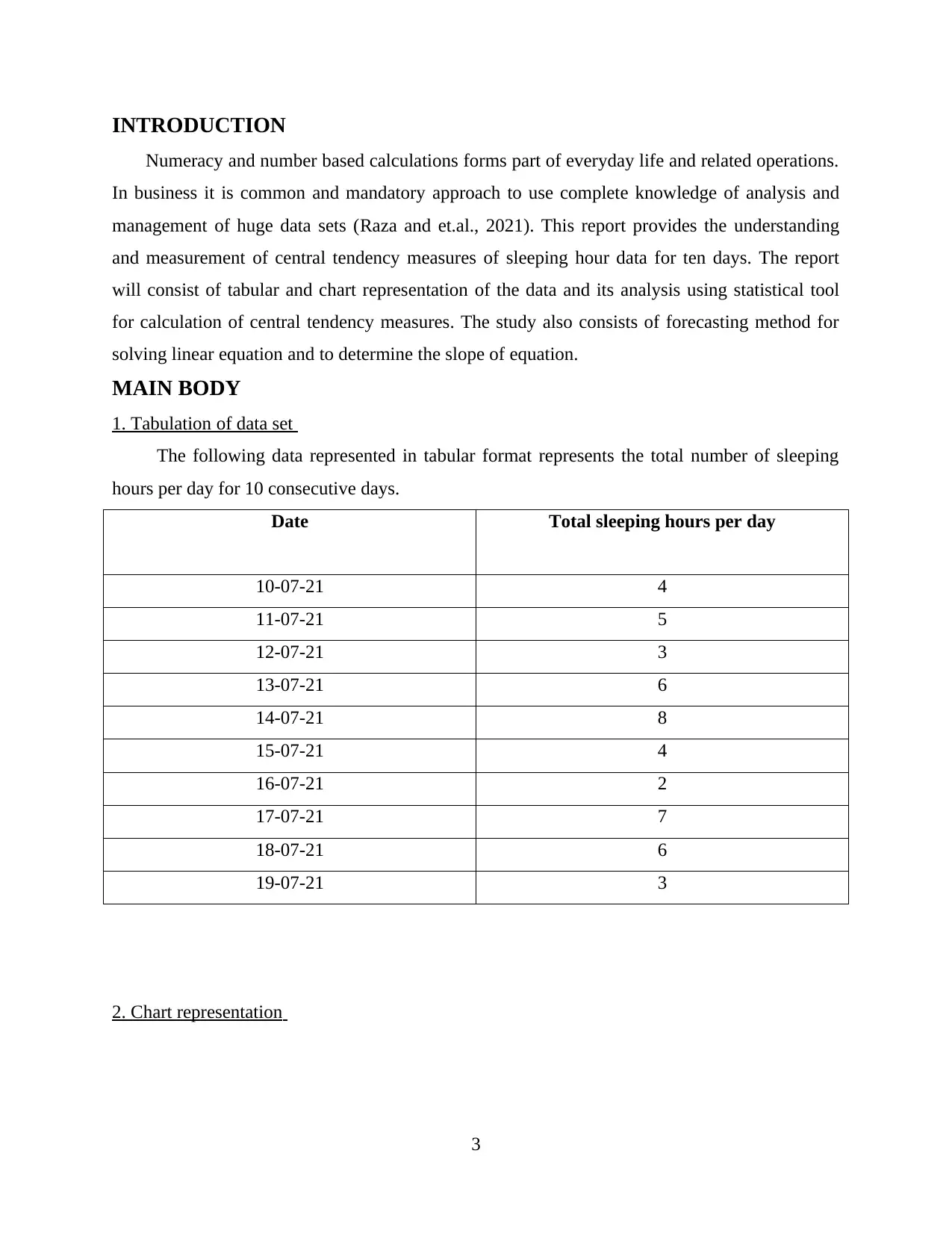
1. Tabulation of data set
The following data represented in tabular format represents the total number of sleeping
hours per day for 10 consecutive days.
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
13-07-21 6
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
2. Chart representation
3
Numeracy and number based calculations forms part of everyday life and related operations.
In business it is common and mandatory approach to use complete knowledge of analysis and
management of huge data sets (Raza and et.al., 2021). This report provides the understanding
and measurement of central tendency measures of sleeping hour data for ten days. The report
will consist of tabular and chart representation of the data and its analysis using statistical tool
for calculation of central tendency measures. The study also consists of forecasting method for
solving linear equation and to determine the slope of equation.
MAIN BODY
1. Tabulation of data set
The following data represented in tabular format represents the total number of sleeping
hours per day for 10 consecutive days.
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
13-07-21 6
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
2. Chart representation
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
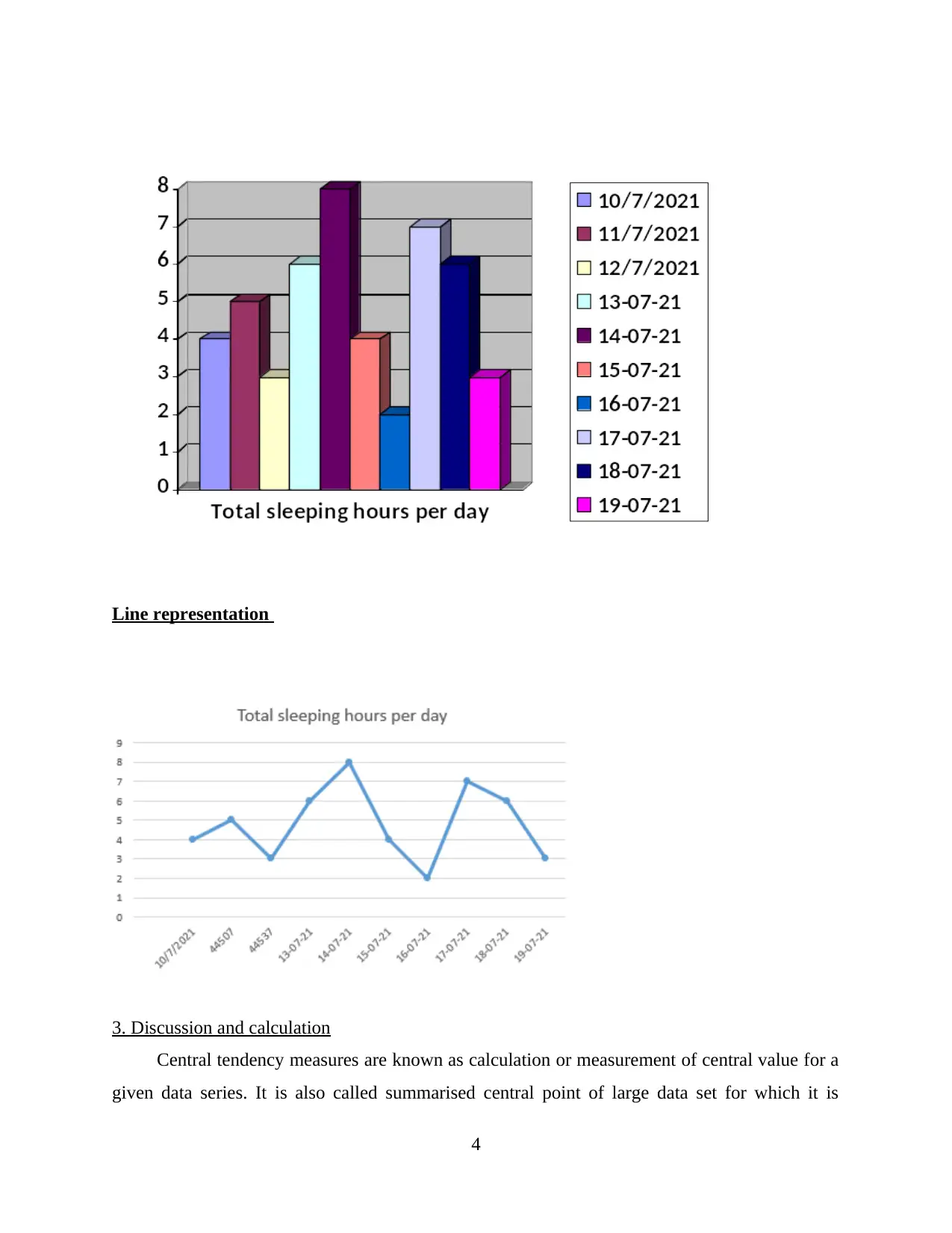
Line representation
3. Discussion and calculation
Central tendency measures are known as calculation or measurement of central value for a
given data series. It is also called summarised central point of large data set for which it is
4
3. Discussion and calculation
Central tendency measures are known as calculation or measurement of central value for a
given data series. It is also called summarised central point of large data set for which it is
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
required to determine the central tendency (Zarie, Hajghassem and Majd, 2018). Central
tendency has three key measures which are known as median, mean and mode respectively. For
the given data set number of sleeping hours per day for 10 consecutive days these three measures
are given as follows:
Calculation of mean
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
13-07-21 6
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
Number of observations (n) 10
Total 48
Mean value 4.8 hours
Mean is known as one of the most common method to measure for analysing data sets
and to outline the average value of data (Belan, 2020). It is considered as effective way for
central tendency measurement. Mean or average value can be calculated by addition of given
data set values and then by dividing them with total number of values or observations. (Mean =
Sum of all values / Total number of values). For the given records of number of sleeping hours, it
has been observed that average sleeping hours are 4.8. It can be generalised that if number of
sleeping hours are above 4.8 hours then it is above average value and if sleeping hours are below
4.8 hours then it is below average or the mean value.
Calculating median
5
tendency has three key measures which are known as median, mean and mode respectively. For
the given data set number of sleeping hours per day for 10 consecutive days these three measures
are given as follows:
Calculation of mean
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
13-07-21 6
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
Number of observations (n) 10
Total 48
Mean value 4.8 hours
Mean is known as one of the most common method to measure for analysing data sets
and to outline the average value of data (Belan, 2020). It is considered as effective way for
central tendency measurement. Mean or average value can be calculated by addition of given
data set values and then by dividing them with total number of values or observations. (Mean =
Sum of all values / Total number of values). For the given records of number of sleeping hours, it
has been observed that average sleeping hours are 4.8. It can be generalised that if number of
sleeping hours are above 4.8 hours then it is above average value and if sleeping hours are below
4.8 hours then it is below average or the mean value.
Calculating median
5
Median is known as the middle value in the data set which distribute or divide complete
data in two parts. To determine the median value, it is required that first data must be arranged in
increasing order. For the data set with odd number of values medium is simply the middle value.
For the data with even number of values as there are two middle values the median is calculated
by finding average of both the middle values. In the given data set there are total 10 number of
values (even) so average of both central or middle values will be calculated.
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
13-07-21 6
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
Number of observations (n) 10
Midpoint = Total no. of observations / 2
= 10/2 =5
So median value = (8+ 4) /2 = 6
Thus median for given data set is 6.
Mode
Mode is known as the data value which has the highest frequency of appearance or which
appears maximum time in data set. For the given data 3 and 4 both are repeating maximum times
and thus they are mode values. Mode is helpful in analysis of trends as it denotes the frequency
of repetition which shows the latest trends.
6
data in two parts. To determine the median value, it is required that first data must be arranged in
increasing order. For the data set with odd number of values medium is simply the middle value.
For the data with even number of values as there are two middle values the median is calculated
by finding average of both the middle values. In the given data set there are total 10 number of
values (even) so average of both central or middle values will be calculated.
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
13-07-21 6
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
Number of observations (n) 10
Midpoint = Total no. of observations / 2
= 10/2 =5
So median value = (8+ 4) /2 = 6
Thus median for given data set is 6.
Mode
Mode is known as the data value which has the highest frequency of appearance or which
appears maximum time in data set. For the given data 3 and 4 both are repeating maximum times
and thus they are mode values. Mode is helpful in analysis of trends as it denotes the frequency
of repetition which shows the latest trends.
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
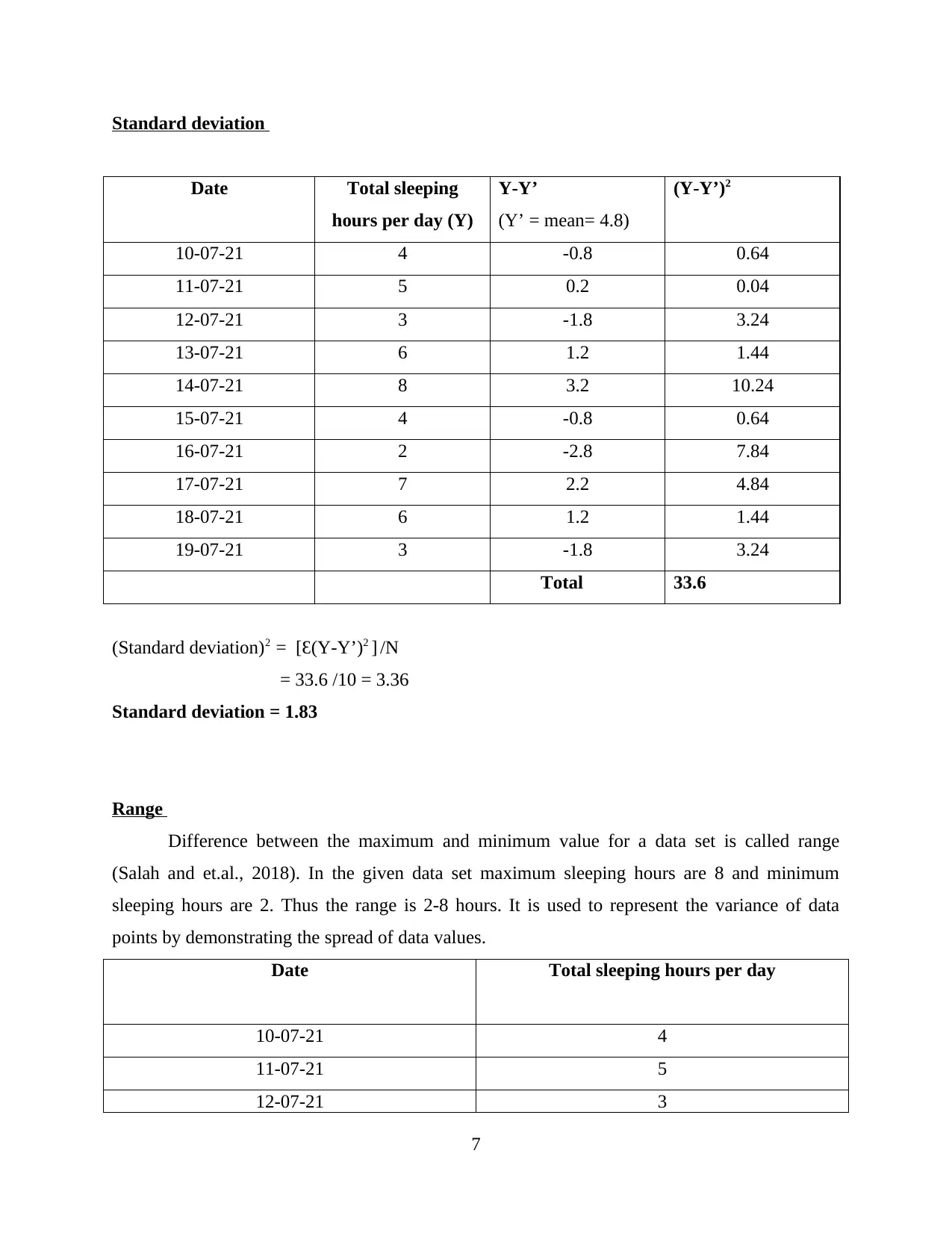
Standard deviation
Date Total sleeping
hours per day (Y)
Y-Y’
(Y’ = mean= 4.8)
(Y-Y’)2
10-07-21 4 -0.8 0.64
11-07-21 5 0.2 0.04
12-07-21 3 -1.8 3.24
13-07-21 6 1.2 1.44
14-07-21 8 3.2 10.24
15-07-21 4 -0.8 0.64
16-07-21 2 -2.8 7.84
17-07-21 7 2.2 4.84
18-07-21 6 1.2 1.44
19-07-21 3 -1.8 3.24
Total 33.6
(Standard deviation)2 = [Ɛ(Y-Y’)2 ] /N
= 33.6 /10 = 3.36
Standard deviation = 1.83
Range
Difference between the maximum and minimum value for a data set is called range
(Salah and et.al., 2018). In the given data set maximum sleeping hours are 8 and minimum
sleeping hours are 2. Thus the range is 2-8 hours. It is used to represent the variance of data
points by demonstrating the spread of data values.
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
7
Date Total sleeping
hours per day (Y)
Y-Y’
(Y’ = mean= 4.8)
(Y-Y’)2
10-07-21 4 -0.8 0.64
11-07-21 5 0.2 0.04
12-07-21 3 -1.8 3.24
13-07-21 6 1.2 1.44
14-07-21 8 3.2 10.24
15-07-21 4 -0.8 0.64
16-07-21 2 -2.8 7.84
17-07-21 7 2.2 4.84
18-07-21 6 1.2 1.44
19-07-21 3 -1.8 3.24
Total 33.6
(Standard deviation)2 = [Ɛ(Y-Y’)2 ] /N
= 33.6 /10 = 3.36
Standard deviation = 1.83
Range
Difference between the maximum and minimum value for a data set is called range
(Salah and et.al., 2018). In the given data set maximum sleeping hours are 8 and minimum
sleeping hours are 2. Thus the range is 2-8 hours. It is used to represent the variance of data
points by demonstrating the spread of data values.
Date Total sleeping hours per day
10-07-21 4
11-07-21 5
12-07-21 3
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
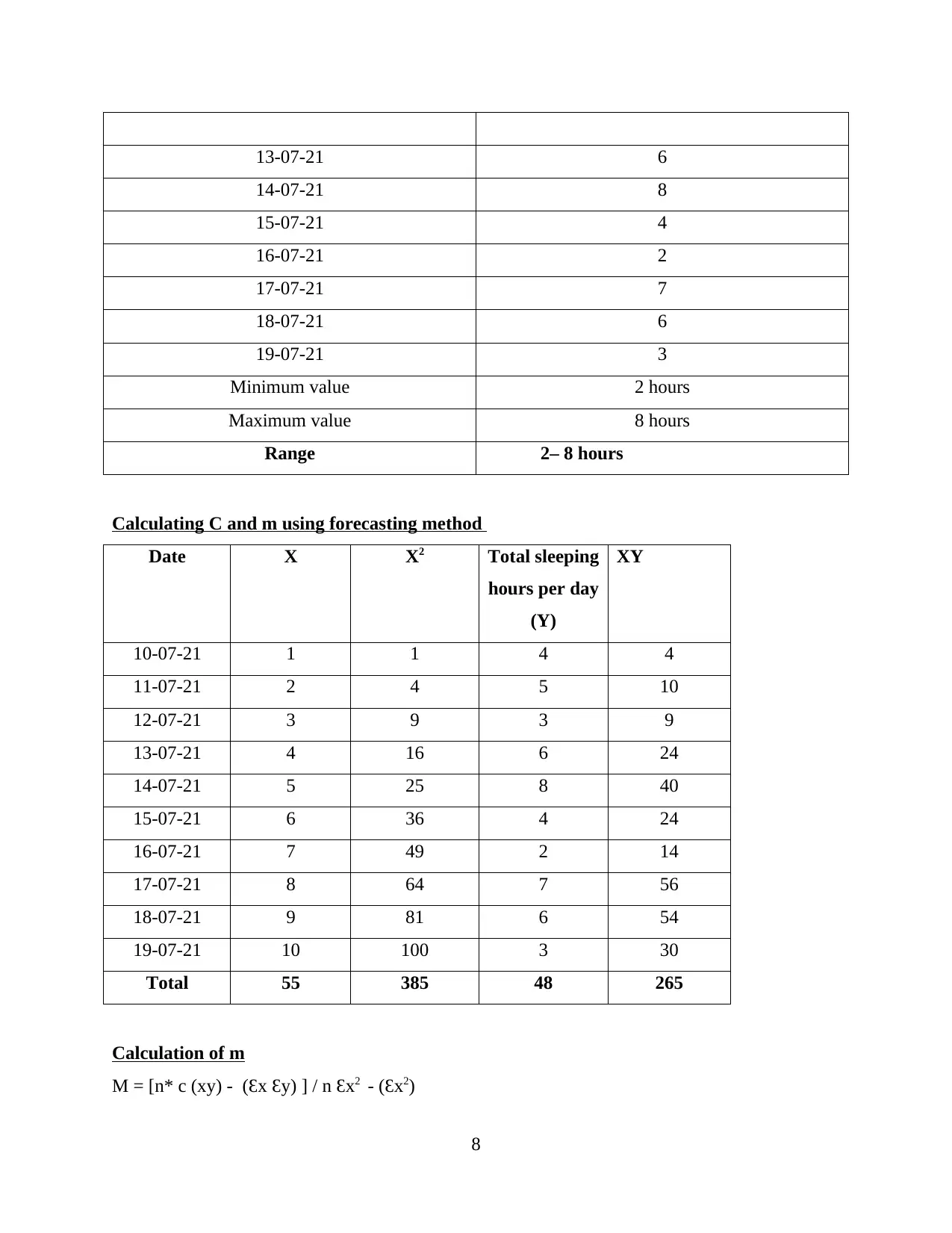
13-07-21 6
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
Minimum value 2 hours
Maximum value 8 hours
Range 2– 8 hours
Calculating C and m using forecasting method
Date X X2 Total sleeping
hours per day
(Y)
XY
10-07-21 1 1 4 4
11-07-21 2 4 5 10
12-07-21 3 9 3 9
13-07-21 4 16 6 24
14-07-21 5 25 8 40
15-07-21 6 36 4 24
16-07-21 7 49 2 14
17-07-21 8 64 7 56
18-07-21 9 81 6 54
19-07-21 10 100 3 30
Total 55 385 48 265
Calculation of m
M = [n* c (xy) - (Ɛx Ɛy) ] / n Ɛx2 - (Ɛx2)
8
14-07-21 8
15-07-21 4
16-07-21 2
17-07-21 7
18-07-21 6
19-07-21 3
Minimum value 2 hours
Maximum value 8 hours
Range 2– 8 hours
Calculating C and m using forecasting method
Date X X2 Total sleeping
hours per day
(Y)
XY
10-07-21 1 1 4 4
11-07-21 2 4 5 10
12-07-21 3 9 3 9
13-07-21 4 16 6 24
14-07-21 5 25 8 40
15-07-21 6 36 4 24
16-07-21 7 49 2 14
17-07-21 8 64 7 56
18-07-21 9 81 6 54
19-07-21 10 100 3 30
Total 55 385 48 265
Calculation of m
M = [n* c (xy) - (Ɛx Ɛy) ] / n Ɛx2 - (Ɛx2)
8

M= [[10* 265] – [48*55]] /(10*385) - (55)2
M = [2650-2640] / [3850-3025]
M= 0.012 or 1%
Calculation of C
C= Ɛy – MƐx / N
C= (48 – [0.012*55])/10
= 47.34/10
C= 4.734
Value forecasting of number of sleeping hours for 12th and 14th day
Y = MX +C
X = 12 Y = 0.012*12+ 4.73 = 4.874
X = 14 Y = 0.012*14+ 4.73 = 4.89
Thus sleeping hours on 12th and 14th days are 4.874 and 4.89 respectively.
CONCLUSION
From the above study it can be concluded that numeracy and measurement of central
tendency plays an important role in logical analysis and evaluation of data.
9
M = [2650-2640] / [3850-3025]
M= 0.012 or 1%
Calculation of C
C= Ɛy – MƐx / N
C= (48 – [0.012*55])/10
= 47.34/10
C= 4.734
Value forecasting of number of sleeping hours for 12th and 14th day
Y = MX +C
X = 12 Y = 0.012*12+ 4.73 = 4.874
X = 14 Y = 0.012*14+ 4.73 = 4.89
Thus sleeping hours on 12th and 14th days are 4.874 and 4.89 respectively.
CONCLUSION
From the above study it can be concluded that numeracy and measurement of central
tendency plays an important role in logical analysis and evaluation of data.
9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

REFERENCES
Books and Journals
Belan, S., 2020. Median and mode in first passage under restart. Physical Review Research. 2(1).
p.013243.
Raza, S.M.M. and et.al., 2021. Conditional mean‐and median‐based cumulative sum control
charts for Weibull data. Quality and Reliability Engineering International. 37(2).
pp.502-526.
Salah, H.B. and et.al., 2018. Mean and median-based nonparametric estimation of returns in
mean-downside risk portfolio frontier. Annals of operations research. 262(2). pp.653-
681.
Zarie, M., Hajghassem, H. and Majd, A.E., 2018. Contrast enhancement using triple dynamic
clipped histogram equalization based on mean or median. Optik. 175. pp.126-137.
10
Books and Journals
Belan, S., 2020. Median and mode in first passage under restart. Physical Review Research. 2(1).
p.013243.
Raza, S.M.M. and et.al., 2021. Conditional mean‐and median‐based cumulative sum control
charts for Weibull data. Quality and Reliability Engineering International. 37(2).
pp.502-526.
Salah, H.B. and et.al., 2018. Mean and median-based nonparametric estimation of returns in
mean-downside risk portfolio frontier. Annals of operations research. 262(2). pp.653-
681.
Zarie, M., Hajghassem, H. and Majd, A.E., 2018. Contrast enhancement using triple dynamic
clipped histogram equalization based on mean or median. Optik. 175. pp.126-137.
10
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





