Report: Analysis and Design of Passive RC and LC Low Pass Filters
VerifiedAdded on 2022/09/07
|18
|1738
|43
Practical Assignment
AI Summary
This assignment analyzes both RC and LC low pass filters, detailing their design, operation, and performance characteristics. The solution includes circuit diagrams, component values, and experimental results obtained through Multisim simulations. It covers the calculation of cutoff frequencies, transfer functions, and two-port network representations for each filter type. The report presents tables of results, graphical measurements, and derivations of transfer functions, including the impact of source and load resistances. Furthermore, it compares the theoretical and experimental results, discusses potential sources of error, and highlights the order of the filters. The analysis includes a comparison of the phase shifts at the cutoff frequencies for both filter types, and concludes with a discussion of the key findings and their implications.

S5.1 Circuit Diagram
S5.2
Output impedance of the function generator, RS = 50Ω
Input impedance of the oscilloscope, RL = 1 MΩ
S5.3
Cut off frequency, fc = 10 kHz
S5.4
The cut-off frequency of the filter in question is 10 kHz and is given by the equation
f c= 1
2 π Req C
Req takes into account both the source and load resistance. If the value of capacitance (C) is
chosen to be C=0.01 μF, the resistance is approximately
Req = 1
2 π f c C ≅ 1.591 k Ω
Thus,
Capacitor, C =0.33 F
Resistance, R ≅ 1.591 kΩ
S5.2
Output impedance of the function generator, RS = 50Ω
Input impedance of the oscilloscope, RL = 1 MΩ
S5.3
Cut off frequency, fc = 10 kHz
S5.4
The cut-off frequency of the filter in question is 10 kHz and is given by the equation
f c= 1
2 π Req C
Req takes into account both the source and load resistance. If the value of capacitance (C) is
chosen to be C=0.01 μF, the resistance is approximately
Req = 1
2 π f c C ≅ 1.591 k Ω
Thus,
Capacitor, C =0.33 F
Resistance, R ≅ 1.591 kΩ
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
S5.5
Find an attached file of the RC circuit as built in multism
S5.6
The preferred standard manufactured values for the capacitor and the resistor are:
Capacitor, C = (10 + 000 +/- 5%) pF = 0.01∓5 % μ F
Resistance, R ≅ 16 x 102 ∓5 % Ω=1.6 ∓5 %k Ω
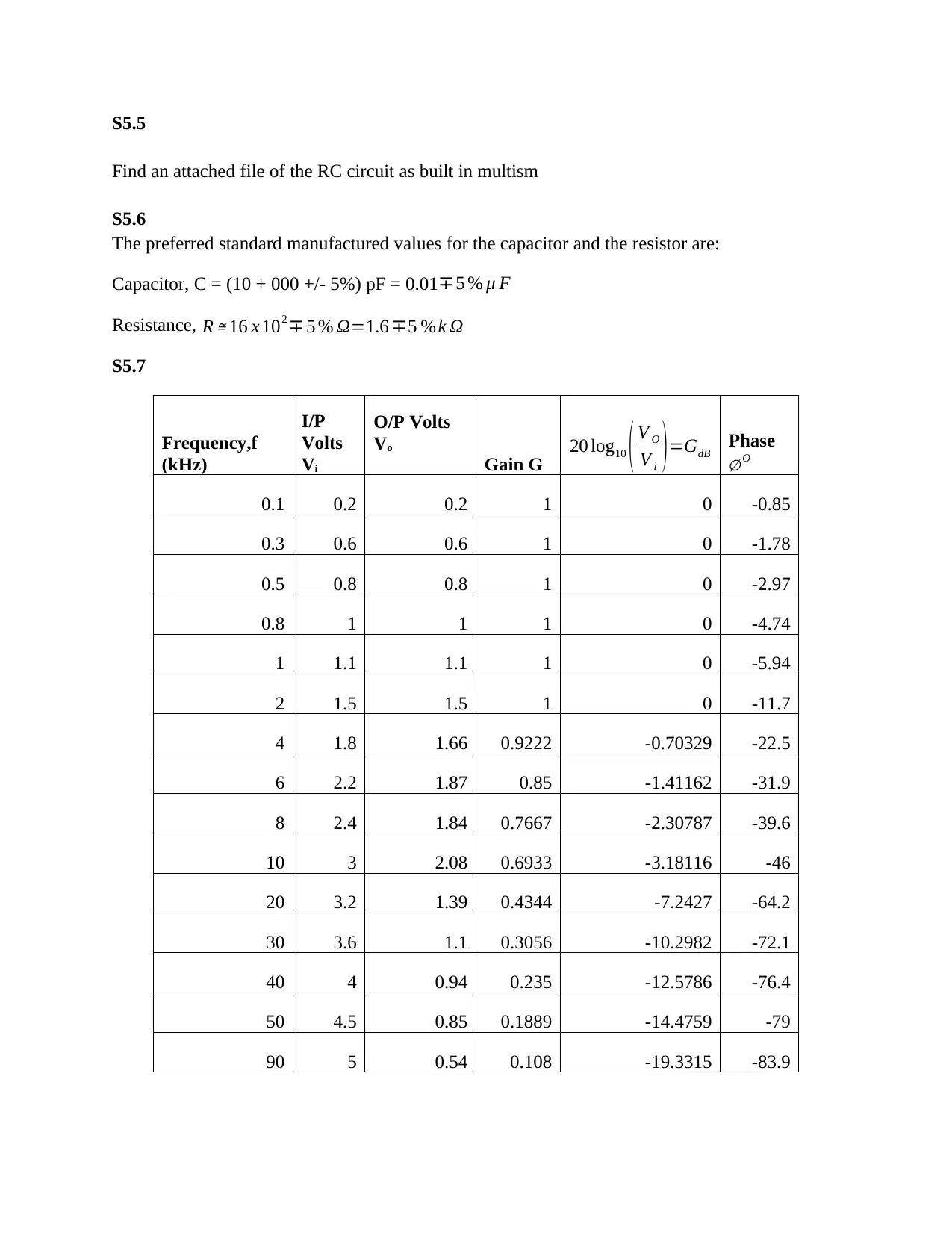
S5.7
Frequency,f
(kHz)
I/P
Volts
Vi
O/P Volts
Vo
Gain G 20 log10 ( V O
V i ) =GdB Phase
∅ O
0.1 0.2 0.2 1 0 -0.85
0.3 0.6 0.6 1 0 -1.78
0.5 0.8 0.8 1 0 -2.97
0.8 1 1 1 0 -4.74
1 1.1 1.1 1 0 -5.94
2 1.5 1.5 1 0 -11.7
4 1.8 1.66 0.9222 -0.70329 -22.5
6 2.2 1.87 0.85 -1.41162 -31.9
8 2.4 1.84 0.7667 -2.30787 -39.6
10 3 2.08 0.6933 -3.18116 -46
20 3.2 1.39 0.4344 -7.2427 -64.2
30 3.6 1.1 0.3056 -10.2982 -72.1
40 4 0.94 0.235 -12.5786 -76.4
50 4.5 0.85 0.1889 -14.4759 -79
90 5 0.54 0.108 -19.3315 -83.9
Find an attached file of the RC circuit as built in multism
S5.6
The preferred standard manufactured values for the capacitor and the resistor are:
Capacitor, C = (10 + 000 +/- 5%) pF = 0.01∓5 % μ F
Resistance, R ≅ 16 x 102 ∓5 % Ω=1.6 ∓5 %k Ω
S5.7
Frequency,f
(kHz)
I/P
Volts
Vi
O/P Volts
Vo
Gain G 20 log10 ( V O
V i ) =GdB Phase
∅ O
0.1 0.2 0.2 1 0 -0.85
0.3 0.6 0.6 1 0 -1.78
0.5 0.8 0.8 1 0 -2.97
0.8 1 1 1 0 -4.74
1 1.1 1.1 1 0 -5.94
2 1.5 1.5 1 0 -11.7
4 1.8 1.66 0.9222 -0.70329 -22.5
6 2.2 1.87 0.85 -1.41162 -31.9
8 2.4 1.84 0.7667 -2.30787 -39.6
10 3 2.08 0.6933 -3.18116 -46
20 3.2 1.39 0.4344 -7.2427 -64.2
30 3.6 1.1 0.3056 -10.2982 -72.1
40 4 0.94 0.235 -12.5786 -76.4
50 4.5 0.85 0.1889 -14.4759 -79
90 5 0.54 0.108 -19.3315 -83.9
S5.8 & S5.9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

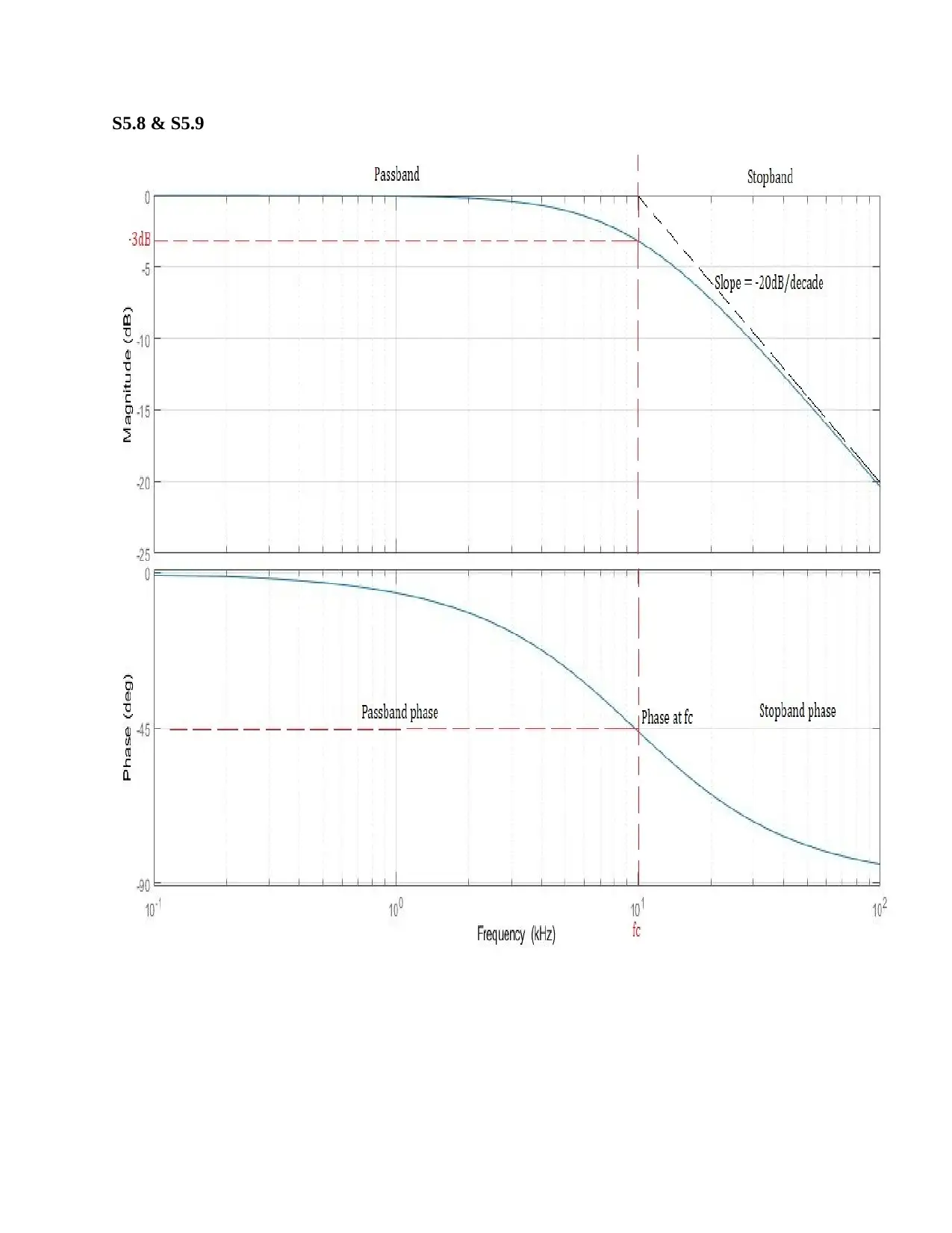
S5.10 Graph Measurements:
S5.10.1 The cut-off frequency is 10 kHz (as indicated on the graphical plots)
f c
actual=10 kHz
S5.10.2 The per decade slope of the gain magnitude is -20dB/decade (as indicated on the
graphical plots)
Sactual
decade =−20 dB /decade
S5.10.3 The per octave slope of the gain magnitude is -6dB/octave (as indicated on the graphical
plots)
Sactual
octave =−6 dB /octave
S5.10.4 The pass band phase is between 0 to -45o (as indicated on the graphical plots). In
radians,
−1
4 π ≤ θactual
pass ≤ 0
S5.10.5 The stop band phase is between -45o to -90o (as indicated on the graphical plots). In
radians,
−π
2 ≤θactual
stop ≤− 1
4 π
S5.10.6 The phase in radians at the cut-off frequency is obtained from the graph as -45o. In
radians,
θactual
cutoff =−45
180 π =−1
4 π rads
S5.10.7 The cut-off frequency obtained from the graph is 10 kHz and that in design specification
is 10 kHz. Therefore the fractional difference is zero i.e.
Ef =0
S5.10.1 The cut-off frequency is 10 kHz (as indicated on the graphical plots)
f c
actual=10 kHz
S5.10.2 The per decade slope of the gain magnitude is -20dB/decade (as indicated on the
graphical plots)
Sactual
decade =−20 dB /decade
S5.10.3 The per octave slope of the gain magnitude is -6dB/octave (as indicated on the graphical
plots)
Sactual
octave =−6 dB /octave
S5.10.4 The pass band phase is between 0 to -45o (as indicated on the graphical plots). In
radians,
−1
4 π ≤ θactual
pass ≤ 0
S5.10.5 The stop band phase is between -45o to -90o (as indicated on the graphical plots). In
radians,
−π
2 ≤θactual
stop ≤− 1
4 π
S5.10.6 The phase in radians at the cut-off frequency is obtained from the graph as -45o. In
radians,
θactual
cutoff =−45
180 π =−1
4 π rads
S5.10.7 The cut-off frequency obtained from the graph is 10 kHz and that in design specification
is 10 kHz. Therefore the fractional difference is zero i.e.
Ef =0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

S5.11 Derivation of the transfer function for the filter circuit
From the equivalent circuit diagram in S.5.1, the transfer function is derived as below
The output voltage is obtained by voltage divider rule as,
V out =
( RL
sC
RL + 1
sC )
(Rs + R+
RL
sC
RL+ 1
sC ) V ¿
Simplifying the expression,
V out =
( RL
1+sC RL )
( Rs + R+ RL
1+ sC RL ) V ¿
On re-arranging, the transfer function for the above filter reduces to,
V out
V ¿
= RL
Rs + R+RL+ sC RL( Rs + R)
But the output impedance of the function generator, RS = 50Ω and the input impedance of the
oscilloscope, RL = 1 MΩ. Substituting these values in the above expression, the transfer function
becomes,
V out
V ¿
= (1 x 106)
50+ R+(1 x 106 )+(1 x 106)sC (50+ R)
The calculated values of the capacitor (C) and the resistor (R) at the cut-off frequency are 0.01
μ F and 1.6 k Ω respectively. Replacing these values in the transfer function above, the equation
reduces to
H ( s )= V out
V ¿
= 106
1001650+ 16.5 s
From the equivalent circuit diagram in S.5.1, the transfer function is derived as below
The output voltage is obtained by voltage divider rule as,
V out =
( RL
sC
RL + 1
sC )
(Rs + R+
RL
sC
RL+ 1
sC ) V ¿
Simplifying the expression,
V out =
( RL
1+sC RL )
( Rs + R+ RL
1+ sC RL ) V ¿
On re-arranging, the transfer function for the above filter reduces to,
V out
V ¿
= RL
Rs + R+RL+ sC RL( Rs + R)
But the output impedance of the function generator, RS = 50Ω and the input impedance of the
oscilloscope, RL = 1 MΩ. Substituting these values in the above expression, the transfer function
becomes,
V out
V ¿
= (1 x 106)
50+ R+(1 x 106 )+(1 x 106)sC (50+ R)
The calculated values of the capacitor (C) and the resistor (R) at the cut-off frequency are 0.01
μ F and 1.6 k Ω respectively. Replacing these values in the transfer function above, the equation
reduces to
H ( s )= V out
V ¿
= 106
1001650+ 16.5 s

The above transfer function is in the s-domain. To convert it the complex frequency domain, s is
replaced with jω. The result is
H ( jω ) = V out
V ¿
= 106
1001650+ j 16.5 ω
S5.12 Derivation of the two port representation of the circuit
The two port network is defined in terms of Z-parameters. For the given RC network, the Z-
parameters are obtained as follows:
Z11= V 1
I1 |(I ¿¿ 2=0)=Rs + R+ 1
jωC ¿
Z21= V 2
I 1 |( I¿¿ 2=0)= 1
jωC ¿
Z22= V 2
I2 |(I ¿¿ 1=0)= 1
jωC ¿
Z12= V 1
I 2 |(I ¿¿ 1=0)= 1
jωC ¿
For C=0.33 F∧R=1.591 kΩ , Rs=50 Ω
Z11=1.591 x 103 +50+ 1
j 2 π x 10 x 0.33 x 103 =1641− j 4.82 x 10−5 Ω
Z12= 1
j 2 π x 10 x 0.33 x 103 =− j 4.82 x 10−5 Ω
Z22= 1
j 2 π x 10 x 0.33 x 103 =− j 4.82 x 10−5 Ω
Z21= 1
j 2 π x 10 x 0.33 x 103 =− j 4.82 x 10−5 Ω
In matrix form, it is
[ Z ]= [ 1641− j 4.82 x 10−5 − j 4.82 x 10−5
− j 4.82 x 10−5 − j 4.82 x 10−5 ]
replaced with jω. The result is
H ( jω ) = V out
V ¿
= 106
1001650+ j 16.5 ω
S5.12 Derivation of the two port representation of the circuit
The two port network is defined in terms of Z-parameters. For the given RC network, the Z-
parameters are obtained as follows:
Z11= V 1
I1 |(I ¿¿ 2=0)=Rs + R+ 1
jωC ¿
Z21= V 2
I 1 |( I¿¿ 2=0)= 1
jωC ¿
Z22= V 2
I2 |(I ¿¿ 1=0)= 1
jωC ¿
Z12= V 1
I 2 |(I ¿¿ 1=0)= 1
jωC ¿
For C=0.33 F∧R=1.591 kΩ , Rs=50 Ω
Z11=1.591 x 103 +50+ 1
j 2 π x 10 x 0.33 x 103 =1641− j 4.82 x 10−5 Ω
Z12= 1
j 2 π x 10 x 0.33 x 103 =− j 4.82 x 10−5 Ω
Z22= 1
j 2 π x 10 x 0.33 x 103 =− j 4.82 x 10−5 Ω
Z21= 1
j 2 π x 10 x 0.33 x 103 =− j 4.82 x 10−5 Ω
In matrix form, it is
[ Z ]= [ 1641− j 4.82 x 10−5 − j 4.82 x 10−5
− j 4.82 x 10−5 − j 4.82 x 10−5 ]
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
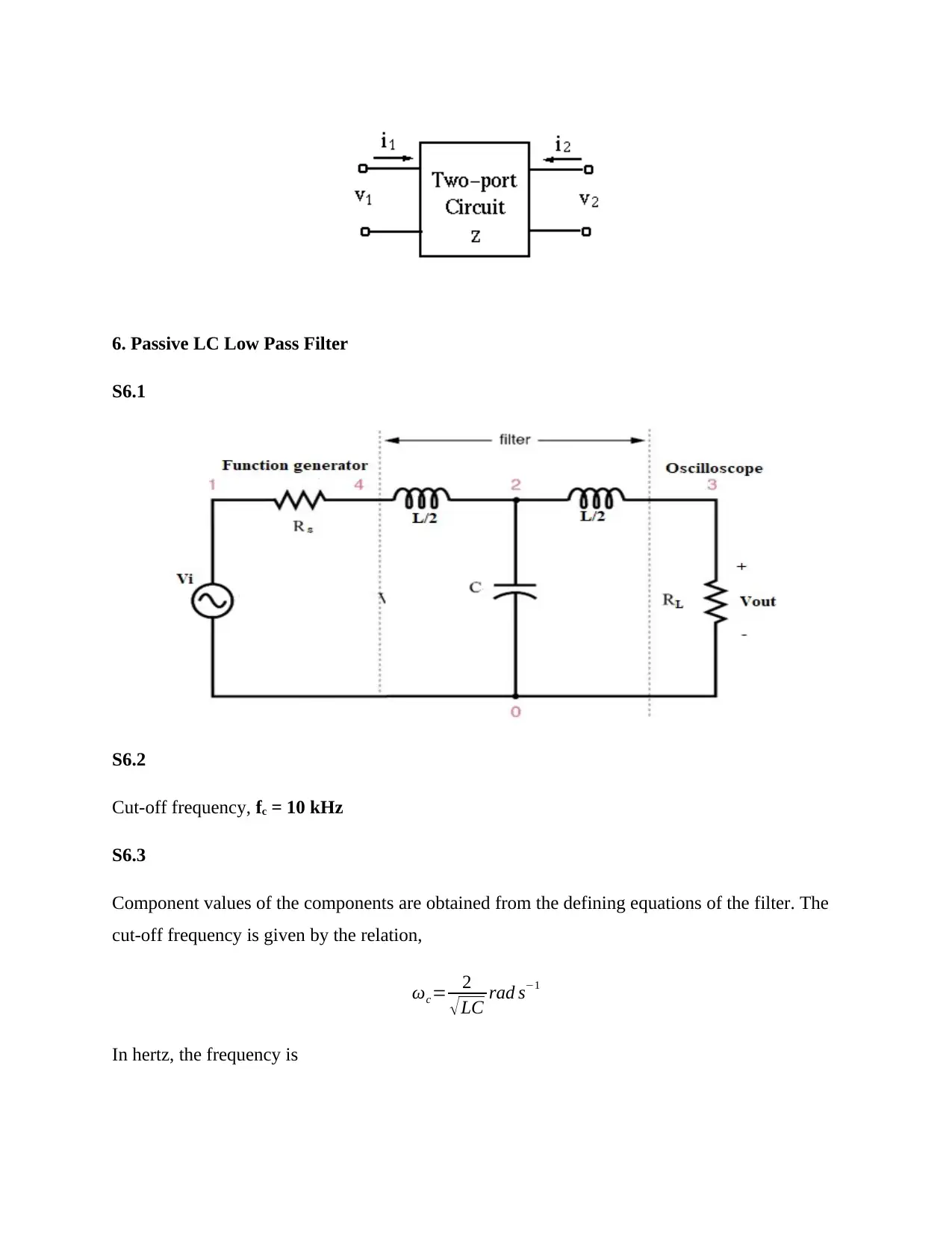
6. Passive LC Low Pass Filter
S6.1
S6.2
Cut-off frequency, fc = 10 kHz
S6.3
Component values of the components are obtained from the defining equations of the filter. The
cut-off frequency is given by the relation,
ωc= 2
√LC rad s−1
In hertz, the frequency is
S6.1
S6.2
Cut-off frequency, fc = 10 kHz
S6.3
Component values of the components are obtained from the defining equations of the filter. The
cut-off frequency is given by the relation,
ωc= 2
√LC rad s−1
In hertz, the frequency is
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

f c= 1
π √ LC
If a capacitor value of 0.1 μ F is chosen, the inductor value is
L= ( 1
π f c √ C )
2
≅ 10.13 mH
The matching impedances Rs and RL are therefore obtained as
Rs=RL= √ L
C ≅ 318.28 Ω
Inductor, L = 10.13 mH
Capacitor, C = 0.1 μ F
S6.4
Find an attached file of the LC circuit as built in multism
S6.5
The standard preferred manufacturer’s values are;
L = (10 + 000 +/- 1%) μ H = 10 mH
C = (10 + 0000 +/- 5%) pF = 0.1∓ 5 % μ F
π √ LC
If a capacitor value of 0.1 μ F is chosen, the inductor value is
L= ( 1
π f c √ C )
2
≅ 10.13 mH
The matching impedances Rs and RL are therefore obtained as
Rs=RL= √ L
C ≅ 318.28 Ω
Inductor, L = 10.13 mH
Capacitor, C = 0.1 μ F
S6.4
Find an attached file of the LC circuit as built in multism
S6.5
The standard preferred manufacturer’s values are;
L = (10 + 000 +/- 1%) μ H = 10 mH
C = (10 + 0000 +/- 5%) pF = 0.1∓ 5 % μ F

S6.6
Table of results
Frequency,f
(kHz)
I/P
Volts
Vi
O/P
Volts
Vo
Gain G 20 log10 ( V O
V i ) =GdB Phase
∅ O
0.1 0.2 0.1 0.5 -6.0206 -1.64
0.3 0.6 0.3 0.5 -6.0206 -3.4
0.5 0.8 0.4 0.5 -6.0206 -5.66
0.8 1 0.5 0.5 -6.0206 -9.06
1 1.1 0.55 0.5 -6.0206 -11.4
2 1.5 0.75 0.5 -6.0206 -22.8
4 1.8 0.9 0.5 -6.0206 -47
6 2.2 1.09 0.49545 -6.0999 -73.9
8 2.4 1.08 0.45 -6.9357 -105
10 3 1.07 0.35667 -8.9547 -136
20 3.2 0.2 0.0625 -24.082 -210
30 3.6 0.07 0.01944 -34.224 -231
Table of results
Frequency,f
(kHz)
I/P
Volts
Vi
O/P
Volts
Vo
Gain G 20 log10 ( V O
V i ) =GdB Phase
∅ O
0.1 0.2 0.1 0.5 -6.0206 -1.64
0.3 0.6 0.3 0.5 -6.0206 -3.4
0.5 0.8 0.4 0.5 -6.0206 -5.66
0.8 1 0.5 0.5 -6.0206 -9.06
1 1.1 0.55 0.5 -6.0206 -11.4
2 1.5 0.75 0.5 -6.0206 -22.8
4 1.8 0.9 0.5 -6.0206 -47
6 2.2 1.09 0.49545 -6.0999 -73.9
8 2.4 1.08 0.45 -6.9357 -105
10 3 1.07 0.35667 -8.9547 -136
20 3.2 0.2 0.0625 -24.082 -210
30 3.6 0.07 0.01944 -34.224 -231
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
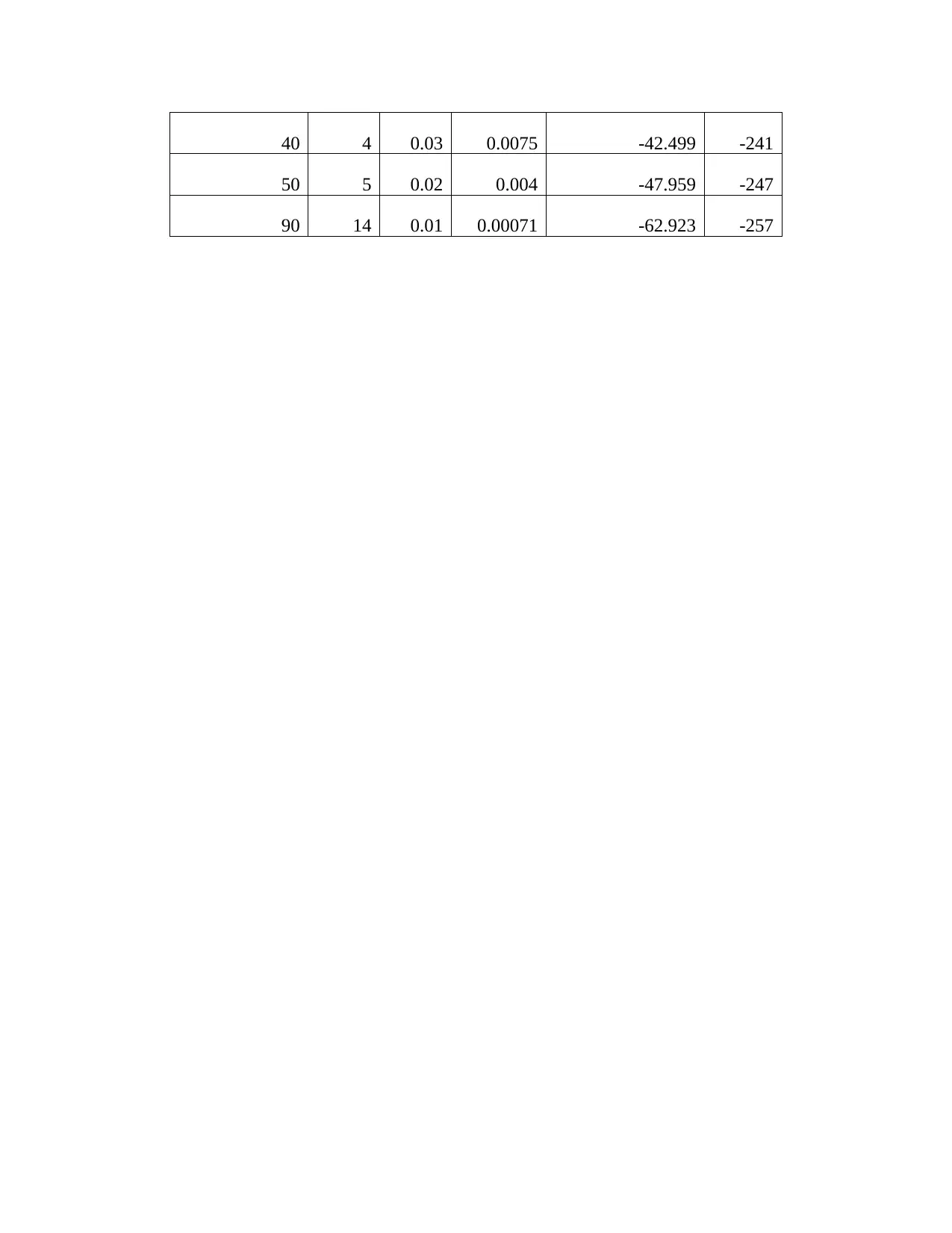
40 4 0.03 0.0075 -42.499 -241
50 5 0.02 0.004 -47.959 -247
90 14 0.01 0.00071 -62.923 -257
50 5 0.02 0.004 -47.959 -247
90 14 0.01 0.00071 -62.923 -257
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
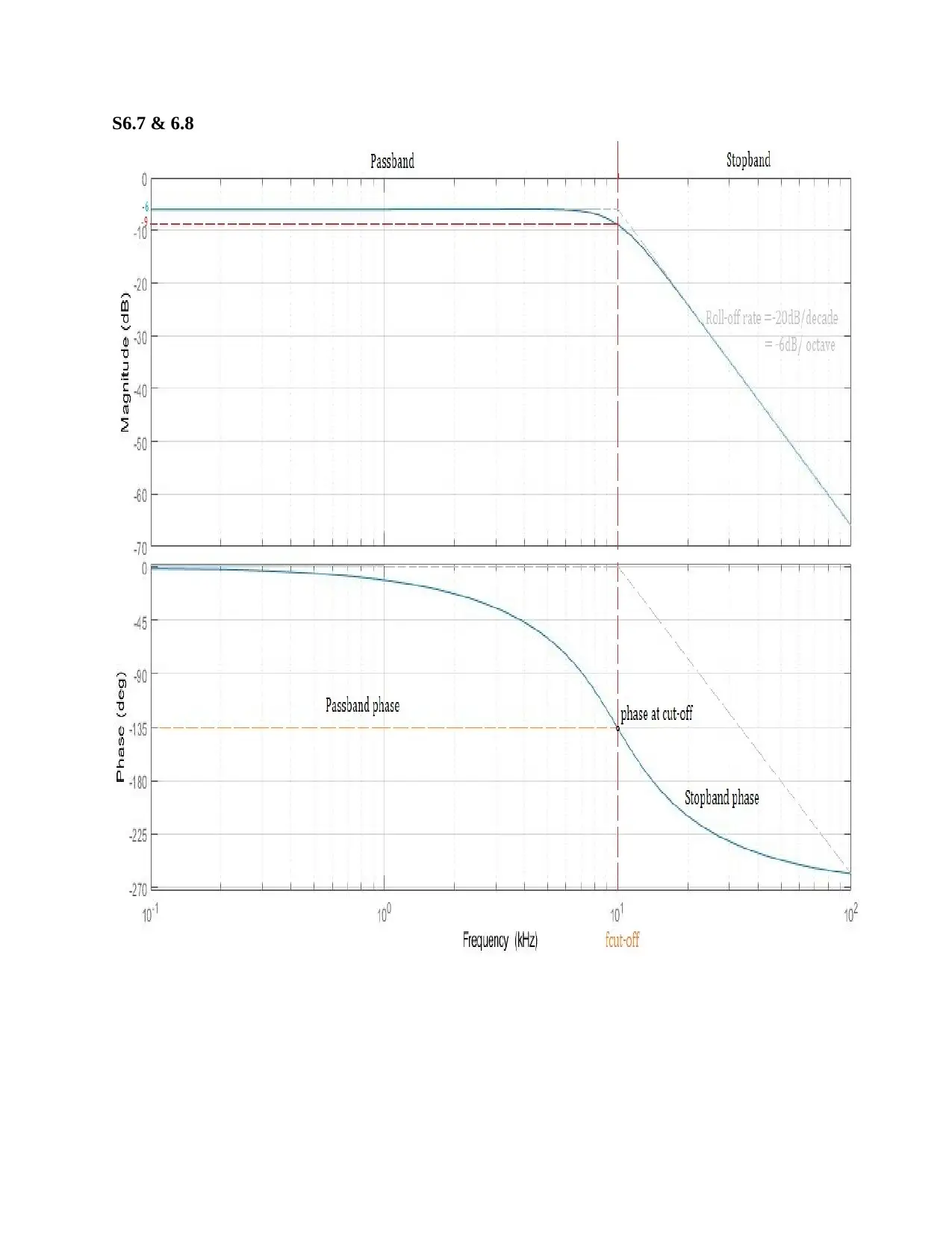
S6.7 & 6.8

S6.9 Graph Measurements:
S6.9.1 The cut-off frequency is 10 kHz (as indicated on the graphical plots)
f c
actual=10 kHz
S6.9.2 The per decade slope of the gain magnitude is -20dB/decade (as indicated on the
graphical plots)
Sactual
decade =−20 dB /decade
S6.9.3 The per octave slope of the gain magnitude is -6dB/octave (as indicated on the graphical
plots)
Sactual
octave =−6 dB /octave
S6.9.4 The pass band phase is between 0 to -135o i.e. angles greater than -135 degrees (as
indicated on the graphical plots). In radians,
−3
4 π ≤θactual
pass ≤0
S6.9.5 The stop band phase is between -135o to -360o i.e. angles less than 135 degrees (as
indicated on the graphical plots)
−2 π ≤ θactual
stop ≤− 3
4 π
S6.9.6 The phase in radians at the cut-off frequency is obtained from the graph as
θactual
cutoff =−135
180 π=−3
4 π rads
S6.9.7 The cut-off frequency obtained from the graph is 10 kHz and that in design specification
is 10 kHz. Therefore the fractional difference is zero i.e.
Ef =0
S6.9.1 The cut-off frequency is 10 kHz (as indicated on the graphical plots)
f c
actual=10 kHz
S6.9.2 The per decade slope of the gain magnitude is -20dB/decade (as indicated on the
graphical plots)
Sactual
decade =−20 dB /decade
S6.9.3 The per octave slope of the gain magnitude is -6dB/octave (as indicated on the graphical
plots)
Sactual
octave =−6 dB /octave
S6.9.4 The pass band phase is between 0 to -135o i.e. angles greater than -135 degrees (as
indicated on the graphical plots). In radians,
−3
4 π ≤θactual
pass ≤0
S6.9.5 The stop band phase is between -135o to -360o i.e. angles less than 135 degrees (as
indicated on the graphical plots)
−2 π ≤ θactual
stop ≤− 3
4 π
S6.9.6 The phase in radians at the cut-off frequency is obtained from the graph as
θactual
cutoff =−135
180 π=−3
4 π rads
S6.9.7 The cut-off frequency obtained from the graph is 10 kHz and that in design specification
is 10 kHz. Therefore the fractional difference is zero i.e.
Ef =0
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 18
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




