College Algebra - Solved Problems and Examples

This article contains solved problems and examples for College Algebra. It covers topics such as functions, polynomials, and asymptotes. The article also includes practice problems and graphs to help students understand the concepts better.

Running head: COLLEGE ALGEBRA 1
College Algebra
Name
Institution

COLLEGE ALGEBRA 2
Question 1
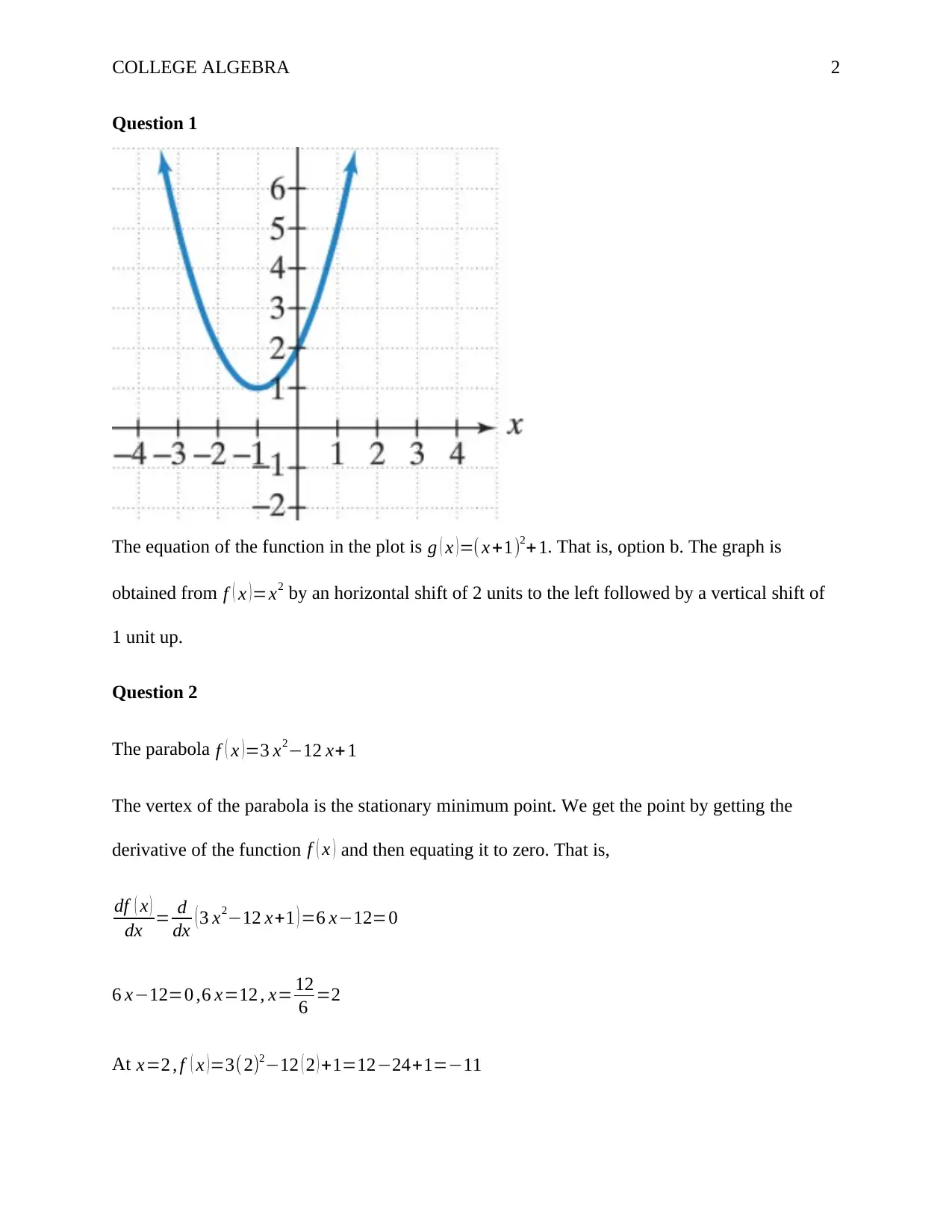
The equation of the function in the plot is g ( x )=( x +1)2+ 1. That is, option b. The graph is
obtained from f ( x )=x2 by an horizontal shift of 2 units to the left followed by a vertical shift of
1 unit up.
Question 2
The parabola f ( x )=3 x2−12 x+ 1
The vertex of the parabola is the stationary minimum point. We get the point by getting the
derivative of the function f ( x ) and then equating it to zero. That is,
df ( x )
dx = d
dx ( 3 x2−12 x+1 ) =6 x−12=0
6 x−12=0 ,6 x=12 , x= 12
6 =2
At x=2 , f ( x ) =3( 2)2−12 ( 2 ) +1=12−24+1=−11

COLLEGE ALGEBRA 3
The vertex is at x=2∧ y=−11. Therefore, the answer is (2,-11), option c.
Question 3
Part a
f ( x )=x2−2 x−3
We have the vertex when, df ( x )
dx =0. That is ,
d
dx ( x2−2 x−3 )=2 x−2=0
2 x−2=0 , 2 x=2 , x= 2
2 =1
When x=1 , f ( x )=12−2 ( 1 )−3=−4
The vertex is at the point (1 ,−4)
The y-intercept is f ( 0 ) =02−2 ( 0 ) −3=0−3=−3
The x-intercept is f ( x )=x2−2 x−3=0
x=2 ± √(−2)2−4 (1×−3)¿ ¿
2× 1= 2 ± √16
2 = 2 ± 4
2 =1 ± 2
x=1+2=3∨x=1−2=−1
Using the obtained vertex and intercepts, we can plot the graph of the function as shown in the
figure below.

COLLEGE ALGEBRA 4
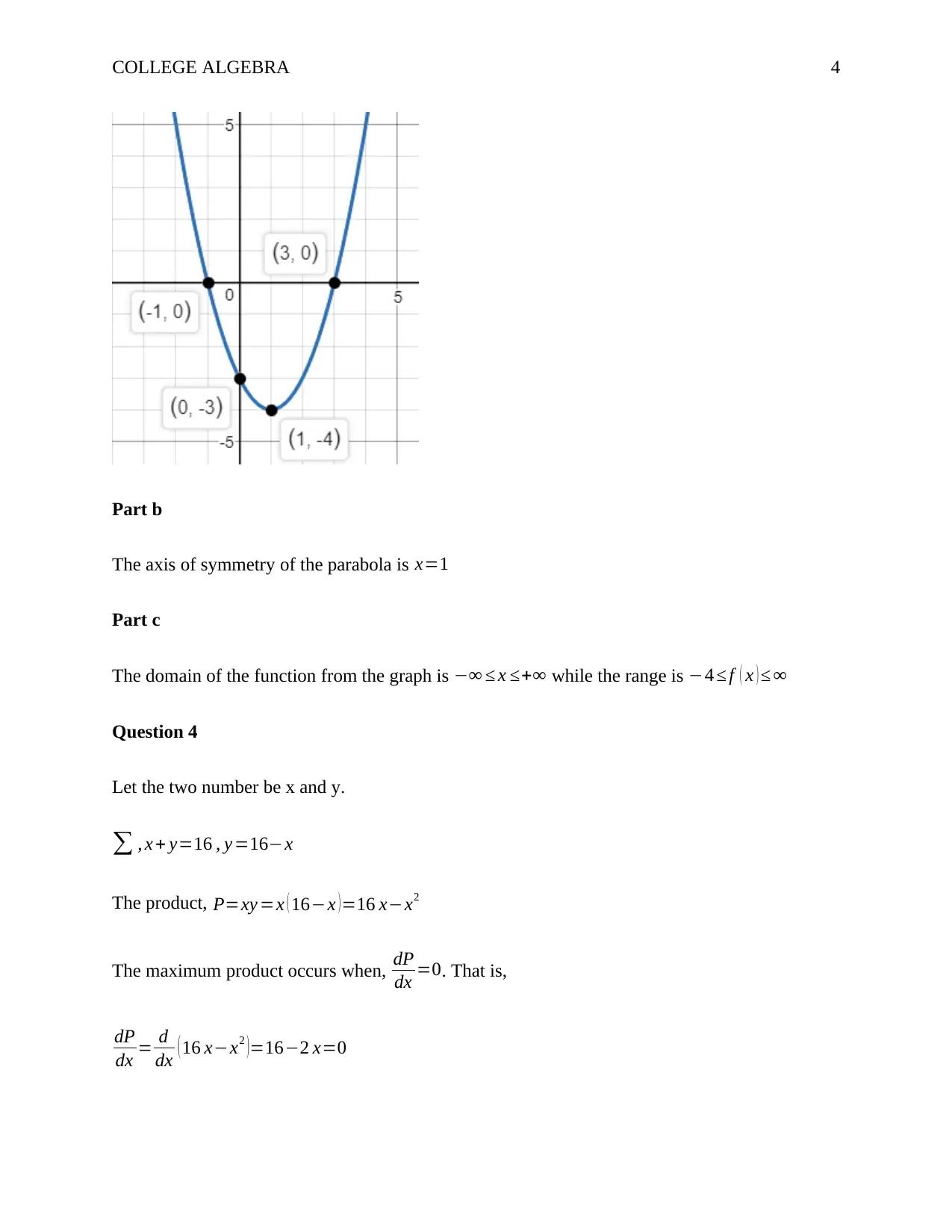
Part b
The axis of symmetry of the parabola is x=1
Part c
The domain of the function from the graph is −∞ ≤ x ≤+∞ while the range is −4 ≤ f ( x ) ≤ ∞
Question 4
Let the two number be x and y.
∑ , x + y=16 , y =16−x
The product, P=xy =x ( 16−x )=16 x−x2
The maximum product occurs when, dP
dx =0. That is,
dP
dx = d
dx ( 16 x−x2 )=16−2 x=0

COLLEGE ALGEBRA 5
16−2 x=0 ,2 x=16 , x= 16
2 =8
when x=8 , y=16−x=16−8=8
The maximum product is xy=8× 8=64
Question 5
The highest power of x in f ( x )=7 x2 +9 x4 is 4. Therefore, the degree of f ( x ) is 4. That is, option
b.
Question 6
f ( x )=11 x3−6 x2+ x+3
The degree of the polynomial is 3 which is odd denoting that its graph will have the dissimilar
behavior at each end. In the function, x3 is the leading term since it has the highest power. The
coefficient of x3 is positive 11. For a polynomial function with an odd degree and positive
leading coefficient, the graph falls to left and rises to the right. That is, option (a).
Question 7
Part a
f ( x )=x4 −6 x3 +9 x2
The degree of the polynomial is 4 which is even denoting that its graph will have the same
behavior at each end. In the function, x4 is the leading term since it has the highest power. The
coefficient of x4 is positive 1. For a polynomial function with an even degree and a positive
leading coefficient, the graph rises to left and to the right.

COLLEGE ALGEBRA 6
Part b
The x-intercepts of f ( x )=x4 −6 x3 +9 x2 occurs when f ( x )=0
f ( x )=x4 −6 x3 +9 x2=0
x4 −6 x3+ 9 x2 =x2 (x ¿¿ 2−6 x +9)=0 ¿
x2=0 , x=0
x2−6 x +9= x2−3 x−3 x +9=0
¿ x ( x−3 ) −3 ( x−3 ) = ( x−3 ) 2=0 , x=3
The x-intercepts are x=0∨x=3
The graph touches the x-axis and turns around at x=0∧x=3
Part c
The y-intercept is f ( x=0 )=04 −6( 0)3 +9 (0)2=0
Part d
The graph of f ( x )=x4 −6 x3 +9 x2 has y-axis symmetry at x=1.5
Part e
Given that f ( x ) =−x4 +4 x2 ,we use the points shown in the table below to sketch its graph.
x -0.5 0 0.5 1 1.5 2 2.5 3 3.5
f ( x ) 3.06
3
0 1.56
3
4 5.063 4 1.563 0 3.063

COLLEGE ALGEBRA 7
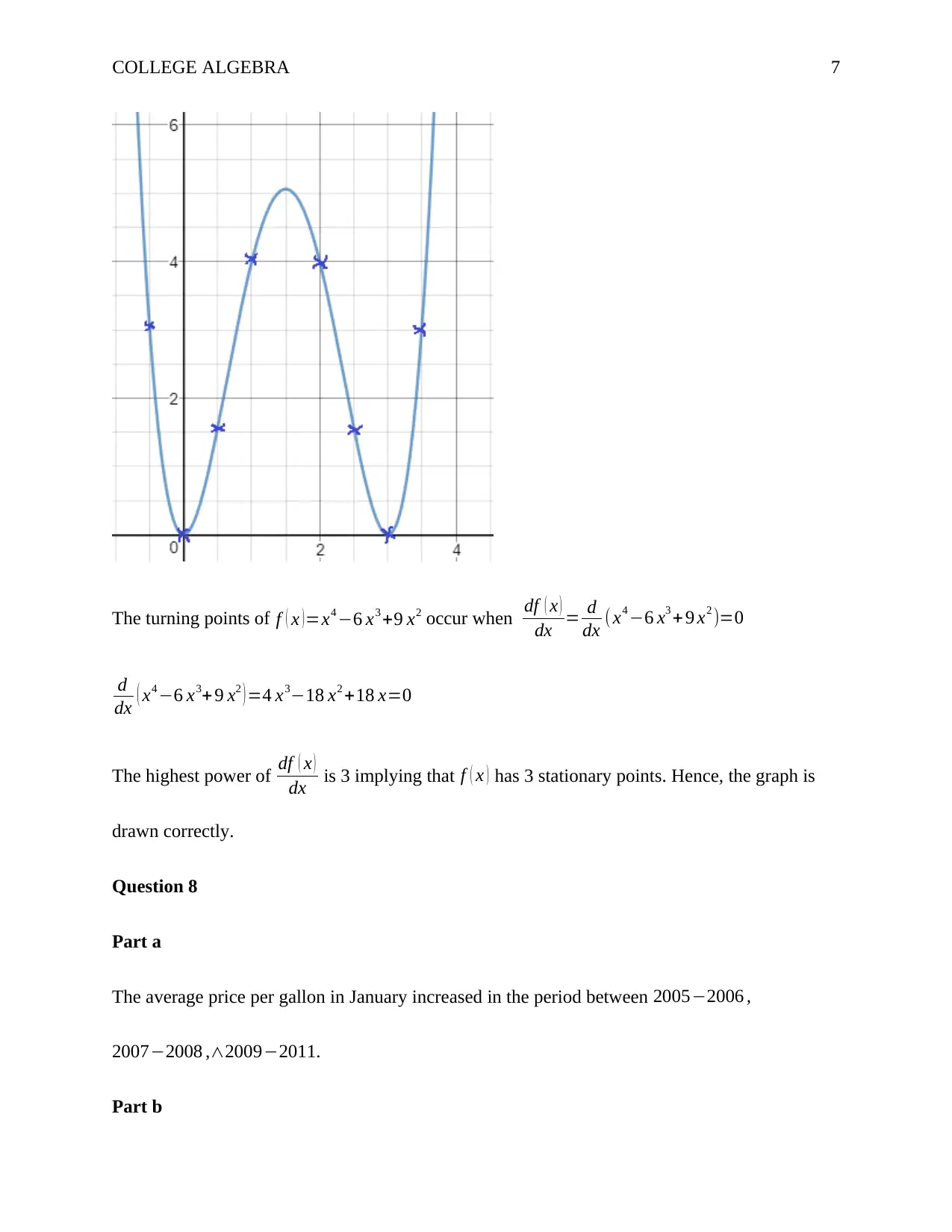
The turning points of f ( x )=x4 −6 x3 +9 x2 occur when df ( x )
dx = d
dx (x4 −6 x3 + 9 x2 )=0
d
dx ( x4 −6 x3+ 9 x2 ) =4 x3−18 x2 +18 x=0
The highest power of df ( x )
dx is 3 implying that f ( x ) has 3 stationary points. Hence, the graph is
drawn correctly.
Question 8
Part a
The average price per gallon in January increased in the period between 2005−2006 ,
2007−2008 ,∧2009−2011.
Part b

COLLEGE ALGEBRA 8
The average price per gallon in January decreased in the period between 2006−2007∧¿
2008−2009.
Part c
The graph has 4 turning points.
Part d
Since the graph has 4 turning points, the degree of the polynomial is 5
Part e
Evidently, we can see from the figure that the graph falls to left and rises to the right. Therefore,
the polynomial function has odd degree and positive leading coefficient.
Part f
Using the graph, we see that the maximum average January price per gallon is $3.15 which
occurred in the year 2011.
Part g
Using the graph, we see that the minimum average January price per gallon is $1.85 which
occurred in the year 2009.
Question 9
2 x5−8 x4 +2 x3 +2 x2
2 x3+1

COLLEGE ALGEBRA 9
2 x5−8 x4 +2 x3 +2 x2
2 x3+1 =x2−4 x+1+ x2+4 x−1
2 x3+1
Therefore, the quotient is x2−4 x+1 while the remainder is x2+ 4 x−1
Question 10
(6 x ¿¿ 5−2 x3+ 4 x2−3 x +1) ÷(x−2)¿

COLLEGE ALGEBRA 10
(6 x ¿¿ 5−2 x3+ 4 x2−3 x +1) ÷(x−2)=6 x4 + 6 x3 +10 x2+ 24 x+ 91
x−2 ¿
Therefore, the quotient ¿ 6 x4 +6 x3 +10 x2 +24 x while the remainder is 91.
Question 11
14 x3−17 x2−16 x−177=0
Part a
Showing that 3 is a solution to the polynomial given using synthetic division.
Using the factor theorem, if a given polynomial say f (x) is divided by x−c and the remainder is
0, then x−c is a factor of f (x) and c is a root of the polynomial equation f ( x )=0.
First, we divide the equation by x−3 and write 3 in place of the divisor followed by the
coefficients of the dividend to the right as shown.
x−3 ⟌ 14 x3−17 x2−16 x−177
3∨14−17−16−17 7
Bring down 14 Multiply 3(14)=42
3| 14 -17 -16 -177 3| 14 -17 -16 -177
↓ ↓ 42
14 14
Then, add : -17+42=25
3| 14 -17 -16 -177
↓ 42
14 25
Multiply: 3(25)=75 Add:-16+75=59
3| 14 -17 -16 -177 3| 14 -17 -16 -177

COLLEGE ALGEBRA 11
↓ 42 75 ↓ 42 75
14 25 14 25 59
Multiply: -2(0)=0 Add:-177+177=0
3| 14 -17 -16 -177 3| 14 -17 -16 -177
↓ 42 75177 ↓ 42 75 177
14 25 59 14 25 59 0
Thus, the remainder is the constant in the last column of the bottom row which is 0. Since the
remainder is zero x−3 is a factor of the given polynomial. Hence, 3 is a solution to the equation.
Part b
We substitute 211 into 14 x3−17 x2−16 x−177 to obtain,
14 x3−17 x2−16 x=211−34=177
14 x3−17 x2−16 x−177=0
The equation is similar to the one in part a denoting that the solution to the equation is 3. Hence,
the abdominal width is 3mm.
Question 12
a. As x →−3−¿ ,f (x )→−∞ ¿
b. As x →−3+¿, f ( x ) →+∞ ¿
c. As x → 1−¿ ,f ( x ) →−∞ ¿
d. As x → 1+¿, f ( x ) →+∞ ¿
e. As x →−∞ , f ( x ) → 0
f. As x → ∞ , f ( x ) → 0
Question 13

COLLEGE ALGEBRA 12
h ( x )= x +7
x2 + 4 x−21
h ( x )= x +7
x2 + 4 x−21 = x+ 7
x2 +7 x−3 x−21
¿ x +7
x(x +7)−3( x+ 7)= x +7
(x+7)( x−3)= 1
x−3
as x →+3 , h ( +3 )= 1
3−3 =∞
Therefore, the function has a vertical asymptote x=3. However, there are no holes.
Question 14
h ( x ) = 12 x3
3 x2 +1
Evidently the leading terms in the numerator and denominator have different degrees. That is, the
numerator has degree 3 while the denominator has degree 2. Since the degrees are the same, the
function doesn’t have a horizontal asymptote.
Question 15
h ( x )= 1
(x−3)2 + 2
To obtain h ( x )= 1
(x−3)2 from f ( x )= 1
x2
First, we draw f ( x )= 1
x2 followed a shift of 3 units to the right and then a vertical shift of 2 units
up. The graph of h is shown below.

COLLEGE ALGEBRA 13
x -2 0 2 2.5 3 3.5 4 6 8
g(x) 2.04 2.111 3 6 ∞ 6 3 2.111 2.04