Electrical Engineering: Communication Systems Assignment 2 Solution
VerifiedAdded on 2023/06/04
|12
|1364
|489
Homework Assignment
AI Summary
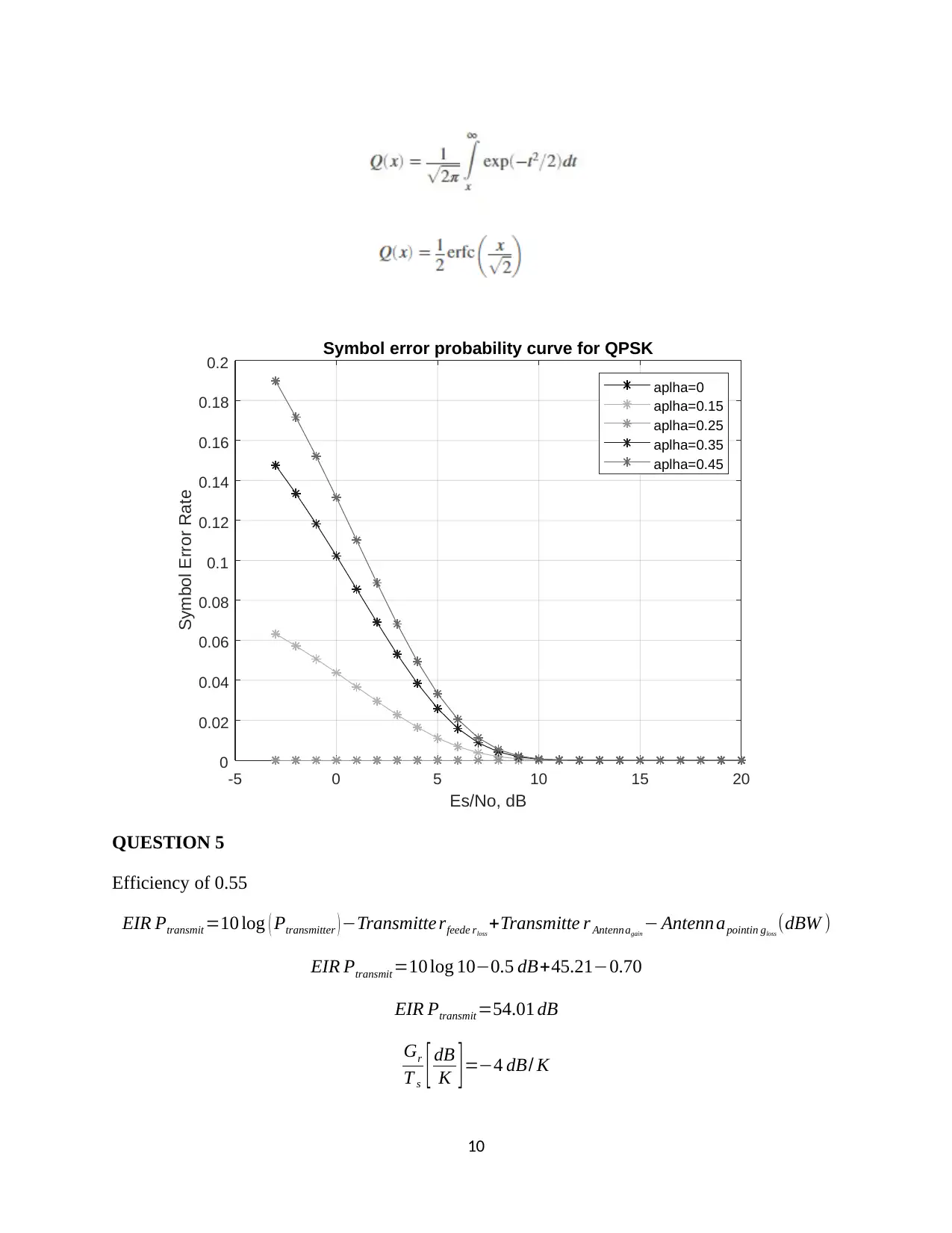
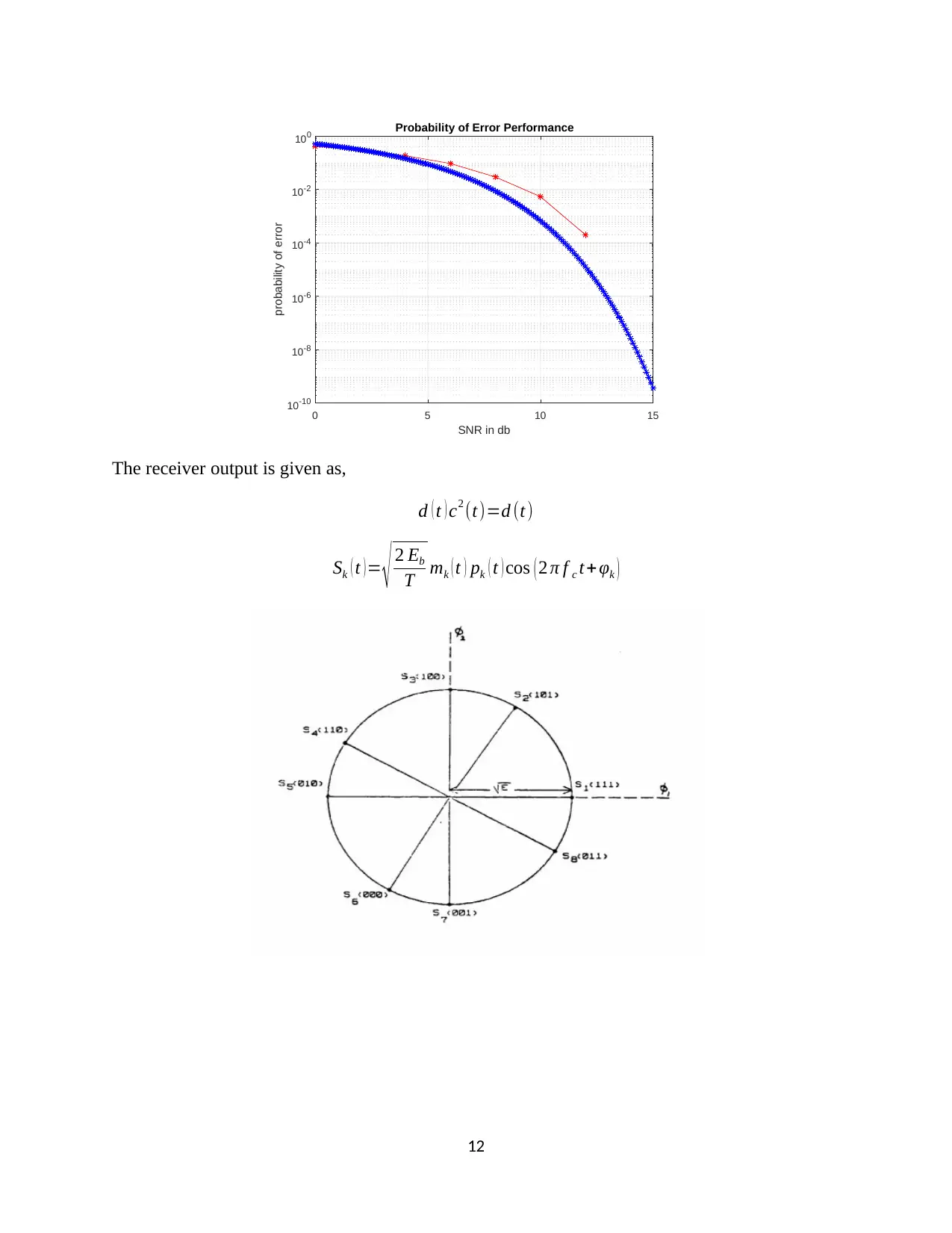
This document presents a comprehensive solution to a Communication Systems assignment, covering a range of topics including matched filters, QPSK modulation, binary communication systems, M-ary PSK, and communication system efficiency. The solution begins with an analysis of a matched filter, deriving its impulse response and Fourier transform, and determining the maximum signal-to-noise ratio. It then delves into QPSK modulation, including signal representation, bit error probability, and MATLAB implementation. The assignment further explores binary communication systems, analyzing a-posteriori probabilities, likelihood ratios, and error probabilities. Additional sections address the efficiency of communication systems, including the impact of data rates and the analysis of signal-to-noise ratio. The document also includes graphical representations and Matlab implementation to illustrate the concepts and results.
1 out of 12












![[object Object]](/_next/static/media/star-bottom.7253800d.svg)