Computational Fluid Dynamics: Simple Initial Value Problem and Numerical Method for Predicting Vibration of Cylinder
VerifiedAdded on 2023/06/11
|31
|4457
|143
AI Summary
This article discusses the simple initial value problem and numerical method for predicting vibration of cylinder using Computational Fluid Dynamics. It also covers power and KC number variations. The article provides solved assignments, essays, and dissertations on Desklib.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.
Computational Fluid Dynamics 1
COMPUTATIONAL FLUID DYNAMICS
By Name
Course
Professor
University
City/State
Date
COMPUTATIONAL FLUID DYNAMICS
By Name
Course
Professor
University
City/State
Date
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Computational Fluid Dynamics 2
Part One: Simple initial value problem
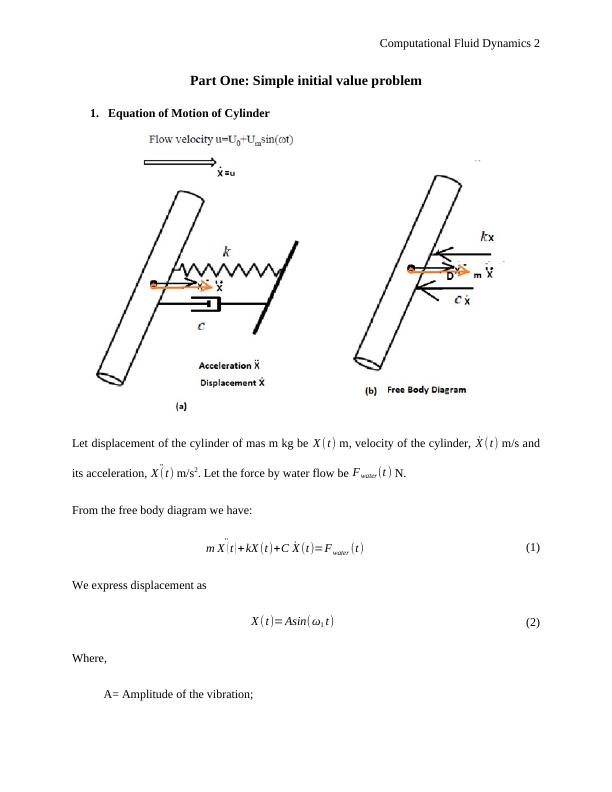
1. Equation of Motion of Cylinder
Let displacement of the cylinder of mas m kg be X (t) m, velocity of the cylinder, ˙X ( t) m/s and
its acceleration, ¨X (t) m/s2. Let the force by water flow be Fwater (t ) N.
From the free body diagram we have:
m ¨X ( t ) +kX (t)+C ˙X (t)=Fwater (t) (1)
We express displacement as
X (t)= Asin(ω1 t) (2)
Where,
A= Amplitude of the vibration;
Part One: Simple initial value problem
1. Equation of Motion of Cylinder
Let displacement of the cylinder of mas m kg be X (t) m, velocity of the cylinder, ˙X ( t) m/s and
its acceleration, ¨X (t) m/s2. Let the force by water flow be Fwater (t ) N.
From the free body diagram we have:
m ¨X ( t ) +kX (t)+C ˙X (t)=Fwater (t) (1)
We express displacement as
X (t)= Asin(ω1 t) (2)
Where,
A= Amplitude of the vibration;
Computational Fluid Dynamics 3
ω1= Angular velocity of the vibration, rad/s.
We therefore have velocity as:
˙X (t)= A ω1 cos (ω1 t ) (3)
And Acceleration as:
¨X (t)=− A ω1
2 sin (ω1 t) (4)
¨X (t)=−ω1
2 X (t) (5)
Force, Fwater, on the cylinder is expressed as:
Fwater ( t ) =CA md
d V r
dt + ρC D Ap
2 |V r|V r (6)
Where,
CD=Coefficient of drag;
C A=Coefficient of inertia;
Ap= Surface area of the cylinder experiencing drag, m2;
|V r|= Magnitude of vibration velocity;
V r=Velocity of flow relative to cylinder, m/s; same as u- ˙X (t );
md=Displacement fluid mass, kg;
ρ= Density of water, kgm-3;
u= Flow velocity, m/s.
ω1= Angular velocity of the vibration, rad/s.
We therefore have velocity as:
˙X (t)= A ω1 cos (ω1 t ) (3)
And Acceleration as:
¨X (t)=− A ω1
2 sin (ω1 t) (4)
¨X (t)=−ω1
2 X (t) (5)
Force, Fwater, on the cylinder is expressed as:
Fwater ( t ) =CA md
d V r
dt + ρC D Ap
2 |V r|V r (6)
Where,
CD=Coefficient of drag;
C A=Coefficient of inertia;
Ap= Surface area of the cylinder experiencing drag, m2;
|V r|= Magnitude of vibration velocity;
V r=Velocity of flow relative to cylinder, m/s; same as u- ˙X (t );
md=Displacement fluid mass, kg;
ρ= Density of water, kgm-3;
u= Flow velocity, m/s.
Computational Fluid Dynamics 4
Using Equation 6 we have:-
Fwater ( t ) =CA md
d V r
dt + ρC D Ap
2 |V r|V r (7)
u=U0 +Um sin ( ωt )
V r =u− ˙X (t)
V r =U0 +Um sin ( ωt )− A ω1 cos (ω1 t )
d V r
dt =Um ωcos ( ωt )+ A ω1
2 sin(ω1 t)
Fwater ( t ) =CA md U m ωcos ( ωt ) +C A md A ω1
2 sin(ω1 t)+ ρC D A p
2 |V r|( U0 +Um sin ( ωt ) − A ω1 cos(ω1 t ) )
(8)
Equation of motion becomes:
m ¨X ( t ) +kX (t)+C ˙X (t )=C A md Um ωcos ( ωt ) ¿+ CA md A ω1
2 sin(ω1 t)+ ρCD A p
2 |V r|(U 0+ Um sin ( ωt )− A ω1 cos
Which becomes:
( m+C A md ) ¨X ( t ) + ( C+ ρC D Ap
2 |V r|) ˙X +kX ( t ) =C A md Um ωcos ( ωt ) ¿+ ρC D A p
2 |V r|( U0 +Um sin ( ωt ) )
(9)
We will use Euler – Runge Kutta method.
Runge Kutta method is of the form
dy
dx =f ( x , y ) , y ( 0 ) , y0 (10)
Using Equation 6 we have:-
Fwater ( t ) =CA md
d V r
dt + ρC D Ap
2 |V r|V r (7)
u=U0 +Um sin ( ωt )
V r =u− ˙X (t)
V r =U0 +Um sin ( ωt )− A ω1 cos (ω1 t )
d V r
dt =Um ωcos ( ωt )+ A ω1
2 sin(ω1 t)
Fwater ( t ) =CA md U m ωcos ( ωt ) +C A md A ω1
2 sin(ω1 t)+ ρC D A p
2 |V r|( U0 +Um sin ( ωt ) − A ω1 cos(ω1 t ) )
(8)
Equation of motion becomes:
m ¨X ( t ) +kX (t)+C ˙X (t )=C A md Um ωcos ( ωt ) ¿+ CA md A ω1
2 sin(ω1 t)+ ρCD A p
2 |V r|(U 0+ Um sin ( ωt )− A ω1 cos
Which becomes:
( m+C A md ) ¨X ( t ) + ( C+ ρC D Ap
2 |V r|) ˙X +kX ( t ) =C A md Um ωcos ( ωt ) ¿+ ρC D A p
2 |V r|( U0 +Um sin ( ωt ) )
(9)
We will use Euler – Runge Kutta method.
Runge Kutta method is of the form
dy
dx =f ( x , y ) , y ( 0 ) , y0 (10)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Computational Fluid Dynamics 5
Since Runge Kutta is applicable in first order ODE, we shall use it with Euler’s method.
Euler’s method is derived from Taylor’s expansion as in steps below.
X ( x0 +h ) =X ( x0 ) +h X x ( x0 ) +O ( h2 ) (11)
We have
X x ( x0 ) = X ( x0 +h )− X ( x0 )
h +O ( h2 )
h
Taking h=∆ x we have
X x ( x0 ) = X ( x0 +h )− X ( x0 )
∆ x +O ∆ t
Neglecting Oh we have
X x ( x0 ) ≈ X ( x0+ ∆ t ) −X ( x0 )
∆ t (12)
For higher orders, the Euler’s method is given by
X ( t , x0 +∆ t ) =X ( t , x0 ) +∆ t Xx ( t , x0 ) + ( ∆ t ) 2
2 ! Xxx ( t , x0 ) +… (13)
The first two terms of the series gives Taylor’s series and form Runge-Kutta first order method.
Truncating gives Equation 13 gives Runge-Kutta second order formula:
X ( t , x0 +∆ t ) =X ( t , x0 ) +∆ t Xx (t , x0 ) + ( ∆ t )2
2 ! Xxx ( t , x0 )
This was summarized by Runge Kutta as:
Since Runge Kutta is applicable in first order ODE, we shall use it with Euler’s method.
Euler’s method is derived from Taylor’s expansion as in steps below.
X ( x0 +h ) =X ( x0 ) +h X x ( x0 ) +O ( h2 ) (11)
We have
X x ( x0 ) = X ( x0 +h )− X ( x0 )
h +O ( h2 )
h
Taking h=∆ x we have
X x ( x0 ) = X ( x0 +h )− X ( x0 )
∆ x +O ∆ t
Neglecting Oh we have
X x ( x0 ) ≈ X ( x0+ ∆ t ) −X ( x0 )
∆ t (12)
For higher orders, the Euler’s method is given by
X ( t , x0 +∆ t ) =X ( t , x0 ) +∆ t Xx ( t , x0 ) + ( ∆ t ) 2
2 ! Xxx ( t , x0 ) +… (13)
The first two terms of the series gives Taylor’s series and form Runge-Kutta first order method.
Truncating gives Equation 13 gives Runge-Kutta second order formula:
X ( t , x0 +∆ t ) =X ( t , x0 ) +∆ t Xx (t , x0 ) + ( ∆ t )2
2 ! Xxx ( t , x0 )
This was summarized by Runge Kutta as:
Computational Fluid Dynamics 6
yi+1 = yi+ ( a1 k1 +a2 k2 ) h
Where,
k1 =f ( xi , yi)
k 2=f ( xi + p1 h , yi + q11 k 1 h)
Finite Difference approximation
X x ( x0 ) = Xi+1− Xi−1
∆ t (13)
X xx ( t , x0 )= Xi+ 1−2 Xi+ Xi−1
( ∆ t )2 (14)
From the oscillatory component of the equation;
Ft ( t0 ) = Fi+ 1−Fi−1
2 ∆ t (15)
The FDM approximation of equation of motion becomes
( m+C A md ) ¨X ( t )+ (C+ ρC D Ap
2 |V r|) ˙X +kX ( t )=g(t , x ) (16)
Where k = Xx
X
FDM approximation
( m+C A md ) ( Xi +1−2 Xi + Xi−1
( ∆ t )2 ) +( C+ ρC D A p
2 |V r|)( Xi+1− Xi−1
∆ t ) +k Xi−1=Gi−1 (17)
yi+1 = yi+ ( a1 k1 +a2 k2 ) h
Where,
k1 =f ( xi , yi)
k 2=f ( xi + p1 h , yi + q11 k 1 h)
Finite Difference approximation
X x ( x0 ) = Xi+1− Xi−1
∆ t (13)
X xx ( t , x0 )= Xi+ 1−2 Xi+ Xi−1
( ∆ t )2 (14)
From the oscillatory component of the equation;
Ft ( t0 ) = Fi+ 1−Fi−1
2 ∆ t (15)
The FDM approximation of equation of motion becomes
( m+C A md ) ¨X ( t )+ (C+ ρC D Ap
2 |V r|) ˙X +kX ( t )=g(t , x ) (16)
Where k = Xx
X
FDM approximation
( m+C A md ) ( Xi +1−2 Xi + Xi−1
( ∆ t )2 ) +( C+ ρC D A p
2 |V r|)( Xi+1− Xi−1
∆ t ) +k Xi−1=Gi−1 (17)
Computational Fluid Dynamics 7
2. Numerical Method for Predicting Vibration of Cylinder
From Equation 9:
We have:
( m+C A md ) ( Xi +1−2 Xi + Xi−1
( ∆ t )2 ) +k X i−1 =0 (18)
We have
( Xi +1−2 Xi+ Xi−1
( ∆ t )2 )≈ ω1
2 Xi−1 (19)
− ( m+C A md ) ω1
2 Xi−1 +k Xi−1=0 (20)
( m+C A md ) ω1
2 =k (21)
From Equation 21 we have
ω1
2= k
m+C A md
(22)
Natural frequency of cylinder vibration is given by:
2. Numerical Method for Predicting Vibration of Cylinder
From Equation 9:
We have:
( m+C A md ) ( Xi +1−2 Xi + Xi−1
( ∆ t )2 ) +k X i−1 =0 (18)
We have
( Xi +1−2 Xi+ Xi−1
( ∆ t )2 )≈ ω1
2 Xi−1 (19)
− ( m+C A md ) ω1
2 Xi−1 +k Xi−1=0 (20)
( m+C A md ) ω1
2 =k (21)
From Equation 21 we have
ω1
2= k
m+C A md
(22)
Natural frequency of cylinder vibration is given by:
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Computational Fluid Dynamics 8
ω1= √ k
m+C A md
(23)
And that for damping coefficient we have:
2 ζ ω1 ˙X ( t ) =2 ζ ω1 ( Xi +1−Xi−1
∆ t )= ( C+ ρC D Ap
2 |V r|)( Xi +1−Xi−1
∆ t )
Giving
2 ζ=
C+ ρC D Ap
2 |V r|
ω1
ζ = 2C+ ρC D A p|V r|
4 ω1
¿ 2C +ρC D A p |V r|
4 √ k
m+ CA md
(24)
Damped natural frequency is given by:
ωd= √ 1−ζ2 ω1
3. Matlab Coding
Using the given values, we have:
clear all;
close all;
clc;
% Defining variables
ω1= √ k
m+C A md
(23)
And that for damping coefficient we have:
2 ζ ω1 ˙X ( t ) =2 ζ ω1 ( Xi +1−Xi−1
∆ t )= ( C+ ρC D Ap
2 |V r|)( Xi +1−Xi−1
∆ t )
Giving
2 ζ=
C+ ρC D Ap
2 |V r|
ω1
ζ = 2C+ ρC D A p|V r|
4 ω1
¿ 2C +ρC D A p |V r|
4 √ k
m+ CA md
(24)
Damped natural frequency is given by:
ωd= √ 1−ζ2 ω1
3. Matlab Coding
Using the given values, we have:
clear all;
close all;
clc;
% Defining variables
Computational Fluid Dynamics 9
k=200; % spring stiffness in N/m
m=50; % mass of cylinder in kg
CA=1; % Inertia coefficient
D=0.12; % diameter of cylinder in m
w=2; % Angular velocity of oscillatory flow
L=1; % length of cylinder m
rho=1.024; % density of water
tf=100; % Duration of vibration in seconds
x0=0.01; % initial displacement of cylinder
v0=0.01; %initial velocity of cylinder
Um=1.2; % Amplitude of oscillatory flow
U0=0.1*Um; % Steady-state velocity of water, m/s
C=1.0; % Damping coefficient in Ns/m
Cd=1.8; % Coefficient of drag
%% Calculating projected area
Ap=D*L;
%% Calculating the displaced mass
md=(pi/4)*D^2*L*rho;
% Natural frequency of undamped vibration
wn=sqrt(k/(m+CA*md));
% Period
T=2*pi/wn;
k=200; % spring stiffness in N/m
m=50; % mass of cylinder in kg
CA=1; % Inertia coefficient
D=0.12; % diameter of cylinder in m
w=2; % Angular velocity of oscillatory flow
L=1; % length of cylinder m
rho=1.024; % density of water
tf=100; % Duration of vibration in seconds
x0=0.01; % initial displacement of cylinder
v0=0.01; %initial velocity of cylinder
Um=1.2; % Amplitude of oscillatory flow
U0=0.1*Um; % Steady-state velocity of water, m/s
C=1.0; % Damping coefficient in Ns/m
Cd=1.8; % Coefficient of drag
%% Calculating projected area
Ap=D*L;
%% Calculating the displaced mass
md=(pi/4)*D^2*L*rho;
% Natural frequency of undamped vibration
wn=sqrt(k/(m+CA*md));
% Period
T=2*pi/wn;
Computational Fluid Dynamics 10
%% Initializing time increment
t=0:tf/1000:tf;
for t=1:tf
V=sin(wn*t);
u=U0-Um*sin(w*t);
Vr=u-V; % velocity of flow relative to cylinder
Vmag=sqrt(u^2+V^2);
%% Damping ratio zeta
zeta=(2*C+rho*Cd*Ap*Vmag)/(4*wn);
%% Damped natural frequency
wd=sqrt(1-zeta*zeta)*wn;
%% Calculating resultant amplitude, a, phase difference phi, and displacement, x
a=1/(sqrt((C+(rho*Cd*Ap*Vmag/2))^2+(k-(m+CA*md)*wn^2)^2));
phi=atan(C+(rho*Cd*Ap*Vmag/2)/(k-(m+CA*md)*wn^2));
t=0:0.1:20;
x=a*exp(-zeta*wn*t).*sin(wd*t+phi);
plot(t,x)
title('Damped vibration of cylinder')
ylabel(' Response for x (m)')
xlabel(' Response time (s)')
end
%% Initializing time increment
t=0:tf/1000:tf;
for t=1:tf
V=sin(wn*t);
u=U0-Um*sin(w*t);
Vr=u-V; % velocity of flow relative to cylinder
Vmag=sqrt(u^2+V^2);
%% Damping ratio zeta
zeta=(2*C+rho*Cd*Ap*Vmag)/(4*wn);
%% Damped natural frequency
wd=sqrt(1-zeta*zeta)*wn;
%% Calculating resultant amplitude, a, phase difference phi, and displacement, x
a=1/(sqrt((C+(rho*Cd*Ap*Vmag/2))^2+(k-(m+CA*md)*wn^2)^2));
phi=atan(C+(rho*Cd*Ap*Vmag/2)/(k-(m+CA*md)*wn^2));
t=0:0.1:20;
x=a*exp(-zeta*wn*t).*sin(wd*t+phi);
plot(t,x)
title('Damped vibration of cylinder')
ylabel(' Response for x (m)')
xlabel(' Response time (s)')
end
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Computational Fluid Dynamics 11
4. Variation of Power and KC number
Power is given by:
P= 1
T ∫
0
T
V 2 dt
V = A ω1 cos(ω1 t )
P= ( A ω1 )2
T ∫
0
T
cos2 (ω1 t ) dt
P= ( A ω1 ) 2
T [ t
2 + sin ( 2 ω1 t )
4 ω1 ]0
T
P= ( A ω1 )
2
T [ T
2 + sin ( 2ω1 T )
4 ω1 ]
4. Variation of Power and KC number
Power is given by:
P= 1
T ∫
0
T
V 2 dt
V = A ω1 cos(ω1 t )
P= ( A ω1 )2
T ∫
0
T
cos2 (ω1 t ) dt
P= ( A ω1 ) 2
T [ t
2 + sin ( 2 ω1 t )
4 ω1 ]0
T
P= ( A ω1 )
2
T [ T
2 + sin ( 2ω1 T )
4 ω1 ]
Computational Fluid Dynamics 12
P= ( A ω1 )2
[ 1
2 + sin ( 2 ω1 T )
4 ω1 T ]
P= ( A ω1 )2
[ 1
2 + sin ( 2 ω1 T )
8 π ]
KC =U m
D T
T = KC∗D
Um
Matlab Code
clear all;
close all;
clc;
% Defining variables
A=1; % Amplitude of displacement
KC=2:2:20;
C=100; % Coefficient of damping, Ns/m
k=KC/C;
Um=1.2; % amplitude of oscillatory velocity
m=50; % mass of cylinder
CA=1; % Coefficient of inertia
P= ( A ω1 )2
[ 1
2 + sin ( 2 ω1 T )
4 ω1 T ]
P= ( A ω1 )2
[ 1
2 + sin ( 2 ω1 T )
8 π ]
KC =U m
D T
T = KC∗D
Um
Matlab Code
clear all;
close all;
clc;
% Defining variables
A=1; % Amplitude of displacement
KC=2:2:20;
C=100; % Coefficient of damping, Ns/m
k=KC/C;
Um=1.2; % amplitude of oscillatory velocity
m=50; % mass of cylinder
CA=1; % Coefficient of inertia
Computational Fluid Dynamics 13
L=1; % length of cylinder
rho=1.024; % density of water
D=0.12; % cylinder diameter
md=(pi/4)*D^2*L*rho; % displaced mass
wn= sqrt(k/(m+CA*md));
tf=20;
t=0:tf/1000:tf;
for t=1:tf
V=sin(wn*t);
u=U0-Um*sin(w*t);
Vr=u-V; % velocity of flow relative to cylinder
Vmag=sqrt(u^2+V^2);
%% Damping ratio zeta
zeta=(2*C+rho*Cd*Ap*Vmag)/(4*wn);
%% Damped natural frequency
wd=sqrt(1-zeta*zeta)*wn;
%% Calculating resultant amplitude, a, phase difference phi, and displacement, x
a=1/(sqrt((C+(rho*Cd*Ap*Vmag/2))^2+(k-(m+CA*md)*wn^2)^2));
phi=atan(C+(rho*Cd*Ap*Vmag/2)/(k-(m+CA*md)*wn^2));
%% Period
KC=2:2:20;
T=KC*D/Um;
L=1; % length of cylinder
rho=1.024; % density of water
D=0.12; % cylinder diameter
md=(pi/4)*D^2*L*rho; % displaced mass
wn= sqrt(k/(m+CA*md));
tf=20;
t=0:tf/1000:tf;
for t=1:tf
V=sin(wn*t);
u=U0-Um*sin(w*t);
Vr=u-V; % velocity of flow relative to cylinder
Vmag=sqrt(u^2+V^2);
%% Damping ratio zeta
zeta=(2*C+rho*Cd*Ap*Vmag)/(4*wn);
%% Damped natural frequency
wd=sqrt(1-zeta*zeta)*wn;
%% Calculating resultant amplitude, a, phase difference phi, and displacement, x
a=1/(sqrt((C+(rho*Cd*Ap*Vmag/2))^2+(k-(m+CA*md)*wn^2)^2));
phi=atan(C+(rho*Cd*Ap*Vmag/2)/(k-(m+CA*md)*wn^2));
%% Period
KC=2:2:20;
T=KC*D/Um;
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Computational Fluid Dynamics 14
P=(A*wn).^2.*(1/2+(sin(2*wn.*T))/(8*pi));
plot(KC,P)
title('Power versus KC')
ylabel(' Power (w)')
xlabel(' KC ')
Results are shown in the Figure:
5. Variation of Power with C
Power is given by:
P=(A*wn).^2.*(1/2+(sin(2*wn.*T))/(8*pi));
plot(KC,P)
title('Power versus KC')
ylabel(' Power (w)')
xlabel(' KC ')
Results are shown in the Figure:
5. Variation of Power with C
Power is given by:
Computational Fluid Dynamics 15
P= ( A ω1 )2
[ 1
2 + sin ( 2 ω1 T )
8 π ]
KC =U m
D T
T = KC∗D
Um
Matlab Code:
clear all;
close all;
clc;
% Defining variables
A=1; % Amplitude of displacement
C=0.0005:50:2000;
k=0.0005;50:2000;
KC=k.*C;
Um=1.2; % amplitude of oscillatory velocity
m=50; % mass of cylinder
CA=1; % Coefficient of inertia
P= ( A ω1 )2
[ 1
2 + sin ( 2 ω1 T )
8 π ]
KC =U m
D T
T = KC∗D
Um
Matlab Code:
clear all;
close all;
clc;
% Defining variables
A=1; % Amplitude of displacement
C=0.0005:50:2000;
k=0.0005;50:2000;
KC=k.*C;
Um=1.2; % amplitude of oscillatory velocity
m=50; % mass of cylinder
CA=1; % Coefficient of inertia
Computational Fluid Dynamics 16
L=1; % length of cylinder
rho=1.024; % density of water
D=0.12; % cylinder diameter
md=(pi/4)*D^2*L*rho; % displaced mass
wn= sqrt(k.*(1/(m+CA*md)));
%% Period
T=KC.*D/Um;
P=(A*wn).^2.*(1/2+(sin(2*wn.*T))/(8*pi));
plot(C,P)
title('Power versus C')
ylabel(' Power (w)')
xlabel(' Coefficient of damping C ')
Results are in Graph below:
L=1; % length of cylinder
rho=1.024; % density of water
D=0.12; % cylinder diameter
md=(pi/4)*D^2*L*rho; % displaced mass
wn= sqrt(k.*(1/(m+CA*md)));
%% Period
T=KC.*D/Um;
P=(A*wn).^2.*(1/2+(sin(2*wn.*T))/(8*pi));
plot(C,P)
title('Power versus C')
ylabel(' Power (w)')
xlabel(' Coefficient of damping C ')
Results are in Graph below:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Computational Fluid Dynamics 17
6. Time History of each:
Time history for Response for x(t) is given by:
clear all;
close all;
clc;
% Defining variables
CA=1; % Inertia coefficient
6. Time History of each:
Time history for Response for x(t) is given by:
clear all;
close all;
clc;
% Defining variables
CA=1; % Inertia coefficient
Computational Fluid Dynamics 18
D=0.12; % diameter of cylinder in m
Cd=1.8;
m=50;
w=2; % Angular velocity of oscillatory flow
C=1;
L=1; % length of cylinder m
Ap=D*L;
rho=1.024; % density of water
md=pi*rho*D^2/4*L;
Um=1.2;
U0=0.1*Um;
tf=20;
t=0:tf/1000:tf;
for t=1:tf
w=2;
k=200;
wn= sqrt(k/(m+CA*md));
V=sin(wn*t);
u=U0-Um*sin(w*t);
Vr=u-V; % velocity of flow relative to cylinder
Vmag=sqrt(u^2+V^2);
%% Damping ratio zeta
D=0.12; % diameter of cylinder in m
Cd=1.8;
m=50;
w=2; % Angular velocity of oscillatory flow
C=1;
L=1; % length of cylinder m
Ap=D*L;
rho=1.024; % density of water
md=pi*rho*D^2/4*L;
Um=1.2;
U0=0.1*Um;
tf=20;
t=0:tf/1000:tf;
for t=1:tf
w=2;
k=200;
wn= sqrt(k/(m+CA*md));
V=sin(wn*t);
u=U0-Um*sin(w*t);
Vr=u-V; % velocity of flow relative to cylinder
Vmag=sqrt(u^2+V^2);
%% Damping ratio zeta
Computational Fluid Dynamics 19
zeta=(2*C+rho*Cd*Ap*Vmag)/(4*wn);
%% Damped natural frequency
wd=sqrt(1-zeta*zeta)*wn;
%% Calculating resultant amplitude, a, phase difference phi, and displacement, x
a=1/(sqrt((C+(rho*Cd*Ap*Vmag/2))^2+(k-(m+CA*md)*wn^2)^2));
phi=atan(C+(rho*Cd*Ap*Vmag/2)/(k-(m+CA*md)*wn^2));
A=1; % Amplitude of displacement
C=0.0005:50:2000;
KC=k.*C;
Um=1.2; % amplitude of oscillatory velocity
m=50; % mass of cylinder
CA=1; % Coefficient of inertia
L=1; % length of cylinder
rho=1.024; % density of water
D=0.12; % cylinder diameter
md=(pi/4)*D^2*L*rho; % displaced mass
wn= sqrt(k.*(1/(m+CA*md)));
t=0:0.1:20;
x=a*exp(-zeta*wn*t).*sin(wd*t+phi);
T=KC.*D/Um;
T1=2*pi/1.9998;
zeta=(2*C+rho*Cd*Ap*Vmag)/(4*wn);
%% Damped natural frequency
wd=sqrt(1-zeta*zeta)*wn;
%% Calculating resultant amplitude, a, phase difference phi, and displacement, x
a=1/(sqrt((C+(rho*Cd*Ap*Vmag/2))^2+(k-(m+CA*md)*wn^2)^2));
phi=atan(C+(rho*Cd*Ap*Vmag/2)/(k-(m+CA*md)*wn^2));
A=1; % Amplitude of displacement
C=0.0005:50:2000;
KC=k.*C;
Um=1.2; % amplitude of oscillatory velocity
m=50; % mass of cylinder
CA=1; % Coefficient of inertia
L=1; % length of cylinder
rho=1.024; % density of water
D=0.12; % cylinder diameter
md=(pi/4)*D^2*L*rho; % displaced mass
wn= sqrt(k.*(1/(m+CA*md)));
t=0:0.1:20;
x=a*exp(-zeta*wn*t).*sin(wd*t+phi);
T=KC.*D/Um;
T1=2*pi/1.9998;
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Computational Fluid Dynamics 20
v=-a*wn*exp(-zeta*wn*t).*sin(wd*t+phi)+a*wd*exp(-zeta*wn*t).*cos(wd*t+phi);
p=(1*wn)^2/T1*(t/2+(1/(4*wn))*sin(2*wn*t));
subplot(2,1,1)
plot(t,x)
title('Time history for x(t) ')
ylabel(' Response for x in m')
xlabel(' Response time (s)')
subplot(2,1,2)
plot(t,v)
title('Time history for v(t) ')
ylabel(' Response for v in m/s')
xlabel(' Response time (s)')
f1=figure;
figure(f1);
plot(t,p)
title('Time history for power')
ylabel(' Response for Power in W')
xlabel(' time in s')
Time histories are shown:
v=-a*wn*exp(-zeta*wn*t).*sin(wd*t+phi)+a*wd*exp(-zeta*wn*t).*cos(wd*t+phi);
p=(1*wn)^2/T1*(t/2+(1/(4*wn))*sin(2*wn*t));
subplot(2,1,1)
plot(t,x)
title('Time history for x(t) ')
ylabel(' Response for x in m')
xlabel(' Response time (s)')
subplot(2,1,2)
plot(t,v)
title('Time history for v(t) ')
ylabel(' Response for v in m/s')
xlabel(' Response time (s)')
f1=figure;
figure(f1);
plot(t,p)
title('Time history for power')
ylabel(' Response for Power in W')
xlabel(' time in s')
Time histories are shown:
Computational Fluid Dynamics 21
Computational Fluid Dynamics 22
7. How KC and C affects Power generation
KC is directly proportional to period. When KC is increased, response for power increases and
vice versa. Similar situation is realized with C.
7. How KC and C affects Power generation
KC is directly proportional to period. When KC is increased, response for power increases and
vice versa. Similar situation is realized with C.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Computational Fluid Dynamics 23
Part Two: One Dimensional Convectional Diffusion Problem
Convectional diffusion equation is given by:
∂T
∂ t =−u ∂ T
∂ x +α ∂2 T
∂ x2 (1)
By finite difference method,
α T xx−u T x−T t=0
We generate First Order Runge Kutta Method from Taylor’s expansion
T ( x0 +h ) =T ( x0 ) + hT x ( x0 ) +O ( h2 )
We have First Order Runge Kutta as
T ( x0 +h ) =T ( x0 ) + hT x ( x0 )
Which gives
Part Two: One Dimensional Convectional Diffusion Problem
Convectional diffusion equation is given by:
∂T
∂ t =−u ∂ T
∂ x +α ∂2 T
∂ x2 (1)
By finite difference method,
α T xx−u T x−T t=0
We generate First Order Runge Kutta Method from Taylor’s expansion
T ( x0 +h ) =T ( x0 ) + hT x ( x0 ) +O ( h2 )
We have First Order Runge Kutta as
T ( x0 +h ) =T ( x0 ) + hT x ( x0 )
Which gives
Computational Fluid Dynamics 24
T x ( x0 )= T ( x0 +h ) −T ( x0 )
h + O ( h2 )
h
Taking h=∆ x we have
T x ( x0 )= T ( x0 +h ) −T ( x0 )
∆ x +O ∆ x
Neglecting Oh we have
T x ( x0 ) ≈ T ( x0 +∆ x ) −T ( x0 )
∆ x
We have Euler’s method as follows:
T ( t , x0 +∆ x ) =T ( t , x0 ) +T x ( t , x0 ) + ( ∆ x )2
2 ! T xx ( t , x0 ) +…
Truncating gives Runge Kutta second Order as:
T ( t , x0 + ∆ x ) =T ( t , x0 ) +T x ( t , x0 ) + ( ∆ x ) 2
2 ! T xx ( t , x0 )
Boundary conditions:
At x=x0=0 ,t=0∧T =30;
∆ x= 2
2000
∆ x=0.001
xn=x0 +n ∆ x
T x ( x0 )= T ( x0 +∆ x )−T ( x0 )
∆ x
T x ( x0 )= T ( x0 +h ) −T ( x0 )
h + O ( h2 )
h
Taking h=∆ x we have
T x ( x0 )= T ( x0 +h ) −T ( x0 )
∆ x +O ∆ x
Neglecting Oh we have
T x ( x0 ) ≈ T ( x0 +∆ x ) −T ( x0 )
∆ x
We have Euler’s method as follows:
T ( t , x0 +∆ x ) =T ( t , x0 ) +T x ( t , x0 ) + ( ∆ x )2
2 ! T xx ( t , x0 ) +…
Truncating gives Runge Kutta second Order as:
T ( t , x0 + ∆ x ) =T ( t , x0 ) +T x ( t , x0 ) + ( ∆ x ) 2
2 ! T xx ( t , x0 )
Boundary conditions:
At x=x0=0 ,t=0∧T =30;
∆ x= 2
2000
∆ x=0.001
xn=x0 +n ∆ x
T x ( x0 )= T ( x0 +∆ x )−T ( x0 )
∆ x
Computational Fluid Dynamics 25
( ∆ x )2
2 ! T xx ( t , x0 )=T ( t , x0 +∆ x ) −T ( t , x0 ) −T x ( t , x0 )
( ∆ x ) 2
2 ! T xx ( t , x0 )=∆ x T x ( x0 ) −T x ( t , x0 )
T xx ( t , x0 )=2 ( ∆ x T x ( x0 ) −T x ( t , x0 )
( ∆ x )2 )
¿ 2 ( ∆ x−1
( ∆ x )2 )T x ( x0 )
For time we have
T t ( t0 ) ≈ T ( t0 +∆ t )−T ( t0 )
∆ t
Finite Difference approximation
T x ( x0 )= Ti +1−T i−1
2 ∆ x
T xx ( t , x0 )= T i+1−2 T i+T i−1
( ∆ x )2
From the equation;
T t ( t0 )= Ti +1−T i−1
2 ∆ t
Which becomes
( ∆ x )2
2 ! T xx ( t , x0 )=T ( t , x0 +∆ x ) −T ( t , x0 ) −T x ( t , x0 )
( ∆ x ) 2
2 ! T xx ( t , x0 )=∆ x T x ( x0 ) −T x ( t , x0 )
T xx ( t , x0 )=2 ( ∆ x T x ( x0 ) −T x ( t , x0 )
( ∆ x )2 )
¿ 2 ( ∆ x−1
( ∆ x )2 )T x ( x0 )
For time we have
T t ( t0 ) ≈ T ( t0 +∆ t )−T ( t0 )
∆ t
Finite Difference approximation
T x ( x0 )= Ti +1−T i−1
2 ∆ x
T xx ( t , x0 )= T i+1−2 T i+T i−1
( ∆ x )2
From the equation;
T t ( t0 )= Ti +1−T i−1
2 ∆ t
Which becomes
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
Computational Fluid Dynamics 26
T ( t0+ ∆ t )−T ( t0 )
∆t =−u ( T ( x0 +∆ x )−T ( x0 )
∆ x ) +α ( 2 ( ∆ x−1
( ∆ x ) 2 ) T x ( x0 ))
Numerical approximation is given by:
Ti +1−Ti −1
2 ∆ t =−u Ti +1−T i−1
2 ∆ x +α Ti +1−2 Ti +T i−1
( ∆ x ) 2
For
i=1 :200
Matlab
Taking boundary conditions
T ( x0 ) =30;
xi=1=0;
t0=0;
xf =2;
T ( x f )=12;
Code
clear all;
close all;
clc;
dT=(30-12)/200; % elemental change in temperature of soil
T ( t0+ ∆ t )−T ( t0 )
∆t =−u ( T ( x0 +∆ x )−T ( x0 )
∆ x ) +α ( 2 ( ∆ x−1
( ∆ x ) 2 ) T x ( x0 ))
Numerical approximation is given by:
Ti +1−Ti −1
2 ∆ t =−u Ti +1−T i−1
2 ∆ x +α Ti +1−2 Ti +T i−1
( ∆ x ) 2
For
i=1 :200
Matlab
Taking boundary conditions
T ( x0 ) =30;
xi=1=0;
t0=0;
xf =2;
T ( x f )=12;
Code
clear all;
close all;
clc;
dT=(30-12)/200; % elemental change in temperature of soil
Computational Fluid Dynamics 27
j=2; % j based on student ID
T0=30; % Surface temperature
Tf=12; % Initial temperature of soil
dx=(2/200); % elemental distance
prompt = 'Enter value of T, T= '; % Prompt to enter value of temperature
T = input(prompt) % input prompt
m=(T-Tf)/dT; % Number of elements considered
n=ceil(m); % Next integer number of element
prompt = 'Enter value of x, x= '; % Prompt to enter value of x
x = input(prompt) % input prompt
k=x/dx;
p=ceil(k);
i=1:n; % range of elements
u=0.002*(1+j); % value of u
alpha=0.002*(1+j); % value of alpha
T1(i)=12; % initial soil temperature
T(i)=T1+0.5*dT; % Initial value of temperature
T2(i)=T1+dT; % second value of temperature
Tx=(T2(i)-T1(i))/dx; % dT/dx
Txx=(T2(i)-2*T(i)+T1(i))/(dx*dx); % d^2T/dx^2
T3(i)=T1(i)+n*dx*Tx+((dx)^2/2)*Txx; % Temperature at point x
dt(i)=dT./(-u*Tx+alpha*Txx); % Elemental time
t=sum(dt, 'all'); % Time to reach temperature T at point x
j=2; % j based on student ID
T0=30; % Surface temperature
Tf=12; % Initial temperature of soil
dx=(2/200); % elemental distance
prompt = 'Enter value of T, T= '; % Prompt to enter value of temperature
T = input(prompt) % input prompt
m=(T-Tf)/dT; % Number of elements considered
n=ceil(m); % Next integer number of element
prompt = 'Enter value of x, x= '; % Prompt to enter value of x
x = input(prompt) % input prompt
k=x/dx;
p=ceil(k);
i=1:n; % range of elements
u=0.002*(1+j); % value of u
alpha=0.002*(1+j); % value of alpha
T1(i)=12; % initial soil temperature
T(i)=T1+0.5*dT; % Initial value of temperature
T2(i)=T1+dT; % second value of temperature
Tx=(T2(i)-T1(i))/dx; % dT/dx
Txx=(T2(i)-2*T(i)+T1(i))/(dx*dx); % d^2T/dx^2
T3(i)=T1(i)+n*dx*Tx+((dx)^2/2)*Txx; % Temperature at point x
dt(i)=dT./(-u*Tx+alpha*Txx); % Elemental time
t=sum(dt, 'all'); % Time to reach temperature T at point x
Computational Fluid Dynamics 28
xf=p*dx;
T1.5=T3(n);
time=abs(t)
How variation of α affects T1.5
clear all;
close all;
clc;
j=2; % j based on student ID
T0=30; % Surface temperature
dx=(2/200); % elemental distance
prompt = 'Enter value of x, x= '; % Prompt to enter value of x
x = input(prompt) % input prompt
k=x/dx;
p=ceil(k);
i=1:p; % range of elements
dT(i)=(30-12)/200; % elemental change in temperature of soil
u=0.002*(1+j); % value of u
T1(i)=12; % initial soil temperature
T(i)=T1(i)+0.5*dT; % Initial value of temperature
T2(i)=T1(i)+dT; % second value of temperature
Tx=(T2(i)-T1(i))/dx; % dT/dx
Txx=(T2(i)-2*T(i)+T1(i))/(dx*dx); % d^2T/dx^2
xf=p*dx;
T1.5=T3(n);
time=abs(t)
How variation of α affects T1.5
clear all;
close all;
clc;
j=2; % j based on student ID
T0=30; % Surface temperature
dx=(2/200); % elemental distance
prompt = 'Enter value of x, x= '; % Prompt to enter value of x
x = input(prompt) % input prompt
k=x/dx;
p=ceil(k);
i=1:p; % range of elements
dT(i)=(30-12)/200; % elemental change in temperature of soil
u=0.002*(1+j); % value of u
T1(i)=12; % initial soil temperature
T(i)=T1(i)+0.5*dT; % Initial value of temperature
T2(i)=T1(i)+dT; % second value of temperature
Tx=(T2(i)-T1(i))/dx; % dT/dx
Txx=(T2(i)-2*T(i)+T1(i))/(dx*dx); % d^2T/dx^2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Computational Fluid Dynamics 29
alpha=0.0002: 5.36913E-06: (0.0002+149*5.36913E-06);
f (i)= (-u*Tx+alpha.*Txx); % Elemental time
dt(i)=dT./(-u*Tx+alpha.*Txx); % Elemental time
j=1: 1:150;
dT1=0.09
T(j)=12+j.*dT1; % Time to reach temperature T at point x
plot(alpha, T)
title('Soil temperature versus alpha')
ylabel( 'Temperature T')
xlabel( 'Alpha')
The graph shows temperature rise from t=0 to 240 seconds as alpha was varied from 0.0002 to
0.001. The relationship is a linear relationship.
alpha=0.0002: 5.36913E-06: (0.0002+149*5.36913E-06);
f (i)= (-u*Tx+alpha.*Txx); % Elemental time
dt(i)=dT./(-u*Tx+alpha.*Txx); % Elemental time
j=1: 1:150;
dT1=0.09
T(j)=12+j.*dT1; % Time to reach temperature T at point x
plot(alpha, T)
title('Soil temperature versus alpha')
ylabel( 'Temperature T')
xlabel( 'Alpha')
The graph shows temperature rise from t=0 to 240 seconds as alpha was varied from 0.0002 to
0.001. The relationship is a linear relationship.
Computational Fluid Dynamics 30
Conclusion
This report presents initial value problem and one dimensional convective diffusion problem.
Equations of cylinder motion and numerical methods of FDM were used in the analysis. Effects
of varying C and KC on power generated in motion were examined. Matlab codes were
generated and graphs presented.
Conclusion
This report presents initial value problem and one dimensional convective diffusion problem.
Equations of cylinder motion and numerical methods of FDM were used in the analysis. Effects
of varying C and KC on power generated in motion were examined. Matlab codes were
generated and graphs presented.
Computational Fluid Dynamics 31
References
Badruddin, I. A., Khan, A., Idris, M. Y. I., Nik-Ghaali, N., & Al-Rashed, A. A. (2017).
Simplified finite element algorithm to solve conjugate heat and mass transfer in porous
medium. International Journal of Numerical Methods for Heat & Fluid Flow, 27(11),
2481-2507.
Özişik, M. N., Orlande, H. R., Colaço, M. J., & Cotta, R. M. (2017). Finite difference methods in
heat transfer. CRC press.
References
Badruddin, I. A., Khan, A., Idris, M. Y. I., Nik-Ghaali, N., & Al-Rashed, A. A. (2017).
Simplified finite element algorithm to solve conjugate heat and mass transfer in porous
medium. International Journal of Numerical Methods for Heat & Fluid Flow, 27(11),
2481-2507.
Özişik, M. N., Orlande, H. R., Colaço, M. J., & Cotta, R. M. (2017). Finite difference methods in
heat transfer. CRC press.
1 out of 31
Related Documents
![[object Object]](/_next/image/?url=%2F_next%2Fstatic%2Fmedia%2Flogo.6d15ce61.png&w=640&q=75){kind=small}
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.