EGB211 Computer Lab Assignment 2022

1
EGB211 Computer lab assignment
Assessment No: 3
Assessment Type: Individual Computer Lab Assignment
Due Date: Friday, 11th October 2019
Student ID:
Name:

Introduction, Background and Project Overview
A dynamic problem can be split in two steps: obtaining the equation of motion and solving it. To obtain the equation
of motion we use common dynamics theory, such as Newton’s second law. The equation of motion can then be
solved through analytical or numerical techniques. So far, you have mostly looked at analytical solutions to problems,
however, even for simple dynamics problems these can rapidly become complex and unwieldy. In actuality, the
presence of a true analytical solution is rare in many real-world problems and rely on simplifications and assumptions
(e.g. neglecting drag). Numerical solutions on the other hand can be readily used to solve simple and complex
dynamics problems. For numerical solutions the main challenges become computational resources and the elegance of
the model.
Elastic pendulum (also called spring pendulum or swinging spring) is a physical system where a piece of mass is
connected by a spring. Compared with the ideal pendulum, not only angle, but also the length of string (spring) is
changing in the process, which makes the problem nonlinear, and extremely difficult to solve analytically. An
example in reality for elastic pendulum is the bungee jump. In this assignment, we will first try to get the analytical
solution for elastic pendulum with multiple approximations. Then finite difference method will be adopted to get the
numerical solution. In the end, we will try to build up a simple numerical model for the whole bungee jump process.
Figure 1. The schematic graph for an elastic pendulum.
The grey curve is the trajectory of the mass.
Table 1. Physical quantities in the system.
Property Symbol Quantity Unit
Item
Total mass m 0.1 kg
Initial angle θ0 0.05 rad
Initial angular
velocity ˙θ0 0.01 rad/s
Initial radius
velocity ˙r0 0.1 m/s
Spring
Free length l0 20 m
Initial elongation dr0 2 m
Elastic
coefficient k 20 N/m
For the following questions:
 This elastic pendulum is swinging in one plane, so two dimensional coordinate system is adequate to describe
the system.
 The equation of motion for a harmonic oscillator is in the form of :
¨θ ( t ) + a ⋅(θ ( t ) −C)=0( a>0)
a and C are constants, which can vary in different equation of motion, and need to be found by rearranging.
Such form of equation has the analytical solution like:
θ ( t ) = A cos ( ωn ⋅t−ϕ ) +C
Where
Angular frequency ωn= √ a
Amplitude A= √ (θ0 −C)2+ ¿ ¿
Phase ϕ =atan ¿
 Small angle theorem: when θ<5o , sinθ ≈ θ, cosθ ≈ 1.
2
EGB211 Computer lab assignment

Equation of Motion
1. Draw the free body diagram for the elastic pendulum model in the Fig 1. Write down the equations of motion
in polar coordinate systems, and Cartesian coordinate system.
Answer within this box. Change the size of the box if needed.
Below is the free body diagram
Figure 2: Free body diagram of the elastic pendulum.
The forces on the pendulum are weight W and tension T.
In polar coordinates, the equation becomes;
¨θ ( t ) + a. (θ ( t )−C) =0
( ¨r −r ˙θ2) (t) + a. (θ ( t )−C) =0
In Cartesian coordinates, the equation becomes
θ = tan−1 y
x
˙θ = - y
x2 + y2
¨θ = 2 xy
( x2+ y2 ) 2
Therefore in Cartesian coordinates the equation becomes
2 xy
( x2+ y2 )
2 + a.(tan−1 y
x –c) = 0
3
EGB211 Computer lab assignment

Analytical Solution
2. To get the analytical solution, for a tough spring and a small mass, we can use the following assumption:
 The elastic pendulum does harmonic oscillation in θ and r direction.
 In r direction, the oscillation of the spring is the dominate motion, and terms relevant with θ can be
ignored.
 In θ direction, the change of the spring length can be ignored, terms with r can be ignored.
Arrange the equation of motion in polar coordinate system to the harmonic oscillation form: (1) use small
angle theorem first, (2) then delete extra non-linear terms for approximation. Get the analytical solution of
elastic pendulum with the parameters in the table 1.
Answer within this box. Change the size of the box if needed.
In polar coordinates, the equation remains
θ ( t ) = A cos ( ωn ⋅t−ϕ ) +C
When removing the excess terms
θ ( t ) = A cos ( ωn ⋅t−ϕ )
So C= 0
Inserting the terms in the is the analytical solution, we have;
θ ( t ) = √ (θ0−C)2 +¿ ¿
replacing C with zero
θ ( t ) = √ (θ0)2 +¿ ¿
θ ( t ) = √ (0.05)2 +¿ ¿
= ( √0.0025+ 0.01
a )cos ( √a⋅ t−atan ( 0.1
0.05∗√a )
)
4
EGB211 Computer lab assignment

Finite Differences
3. Write down the equation of motion in Cartesian coordinate system from Question 1 in the finite difference
form. State the initial conditions for finite difference method. Show all working.
Answer within this box. Change the size of the box if needed.
xn+1 = x(tn+ Δt ¿
vn+1 = v(tn+ Δt ¿
the respective taylor series now becomes
vn+1=vn+ an Δ t +σ [ ( Δ t )2 ]
xn+1 = xn +vn Δt +1
2 an ( Δ t )2+ σ [ ( Δt )3 ]
The equation of motion can be rewritten as follows;
2 x (t n +Δ t) y (tn + Δt)
¿ ¿ ¿ + a.( tan−1 y (tn + Δ t)
x(tn +Δ t) –c) = 0
5
EGB211 Computer lab assignment

MATLAB Code
4. Show the MATLAB code for solving the finite difference equations obtained in Question 3.
Answer within this box. Change the size of the box if needed.
(Include initialisation based on Question 3. Do not include the code part responsible for the plotting.)
syms mass acc grav angle(t)
% Mass of pendulum is given as 0.1
% acc is the acceleration
% grav is the gravitational forcc
% angle is the theta
equation1 = mass*acc == -mass*grav*sin(angle)
syms r
equation1 = subs(equation1,acc,r*diff(angle,2))
%eqn = isolate(eqn,diff(theta,2)) % isolating the angular acceleration
syms omeg_a
equation1 = subs(equation1,grav/r,omeg_a^2)
% linearizing the equations to solve them analyticcaly
syms exe
approx = taylor(sin(exe),exe,'Order',2);
approx = subs(approx,exe,angle(t))
%
eqnLinear = subs(equation1,sin(angle(t)),approx)
% solving the equation analytically
syms angle_0 angle_t0
angle_t = diff(angle);
cond_itions = [angle(0) == angle_0, angle_t(0) == angle_t0];
assume(omeg_a,'real')
thetaSol(t) = dsolve(eqnLinear,cond_itions)
%%
% PLOTING THE MOTION OF THE PENDULUM
grav_ity = 9.81; % gravity
ra_dius = 2; % length of the pendulum
omega_0_Val = sqrt(grav_ity/ra_dius);
T = 2*pi/omega_0_Val;
%setting the initial conditions
theta_0Val = 0.1*pi; % Solution only valid for small angles.
theta_t0Val = 0; % Initially at rest.
% substituting intial conditions and physical parameters
var_ables = [omeg_a angle_0 angle_t0];
val_ues = [omega_0_Val theta_0Val theta_t0Val];
angle_soln = subs(thetaSol,var_ables,val_ues);
% plotting tjhe harmonic motion
trew=angle_soln(t*T)/pi
%
fplot(trew, [0 5]);
grid on;
title('SPRING Pendulum graph');
xlabel('t/T');
ylabel('\theta/\pi');
6
EGB211 Computer lab assignment

Discretization and Convergence:
5. The accuracy of numerical solution is completely dependent on the timestep dt. The accuracy and the
computational cost both increase indefinitely as dt → 0. Because of this, in practical application of
computational resources, we are only interested in dt which will provide results that do not change/benefit
from any further increase in resolution.
1) Estimate the dt value according to the frequency in Question 2. There should be at least 40 points in one
period in each direction.
2) Plot the trajectory of the elastic pendulum from the numerical solution (x-y plot), with at least 2 periods in
each direction.
Answer within this box. Change the size of the box if needed.
% Finite Difference Approach To solve ODE System of Equations
i=2;
% Specifying Constants
radius=2; muk=0.4;dt = 0.0001;g=32.2;
% Creating Vectors
Theta= []; Velocity = []; time= [];
% Initializing Vectors
Velocity(i)=10; Theta(i)=0; time(i)=0; s(i)=0;
u=time(1);
phi=linspace(0,360,20)
% Testing Whether the Block Leaves the Surface and Evaluating
% The New Positions, Angle, and Velocity of the Block
while cos(Theta(i))-(Velocity(i))^2/(radius*g)>eps
i= i+2;
Velocity(i) = Velocity(i-1)+dt*(g*(sin(Theta(i-1))-muk*cos(Theta(i-1)))
+muk*(Velocity(i-1))^2/radius);
Theta(i)= Theta(i-1)+dt/(2*radius)*(Velocity(i)+Velocity(i-1));
s(i)=s(i-1)+ dt*(Velocity(i)+Velocity(i-1))/2;
time(i)= u+(i-1)*dt;
end
v=sind(phi);
t=linspace(0,2,20);
Theta(i)=((Theta(i)+Theta(i-1))/2);
s2 = radius*Theta(i);
Theta(i) = Theta(i)*180/pi;
Velocity(i) = (Velocity(i)+Velocity(i-1))/2;
s(i) = (s(i)+s(i-1))/2;
% Printing the Results
disp(['Time = %5.4f sec\n',num2str((time(i)))])
disp(['Theta = %5.4f deg\n',num2str((Theta(i)))])
numel(time)
%
plot(t,v)
% v=sind(phi)
Numerical solution VS Analytical solution:
7
EGB211 Computer lab assignment

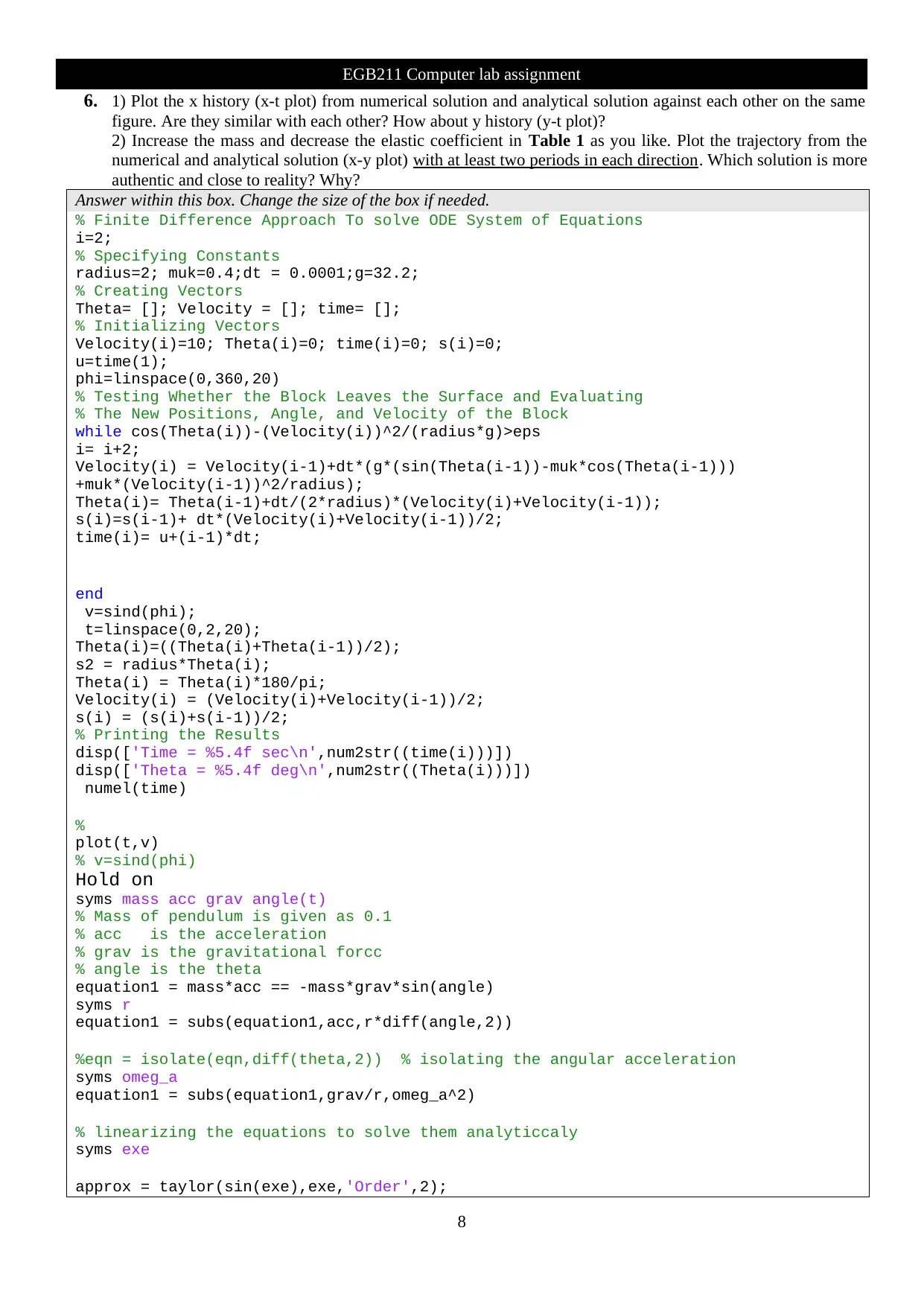
6. 1) Plot the x history (x-t plot) from numerical solution and analytical solution against each other on the same
figure. Are they similar with each other? How about y history (y-t plot)?
2) Increase the mass and decrease the elastic coefficient in Table 1 as you like. Plot the trajectory from the
numerical and analytical solution (x-y plot) with at least two periods in each direction. Which solution is more
authentic and close to reality? Why?
Answer within this box. Change the size of the box if needed.
% Finite Difference Approach To solve ODE System of Equations
i=2;
% Specifying Constants
radius=2; muk=0.4;dt = 0.0001;g=32.2;
% Creating Vectors
Theta= []; Velocity = []; time= [];
% Initializing Vectors
Velocity(i)=10; Theta(i)=0; time(i)=0; s(i)=0;
u=time(1);
phi=linspace(0,360,20)
% Testing Whether the Block Leaves the Surface and Evaluating
% The New Positions, Angle, and Velocity of the Block
while cos(Theta(i))-(Velocity(i))^2/(radius*g)>eps
i= i+2;
Velocity(i) = Velocity(i-1)+dt*(g*(sin(Theta(i-1))-muk*cos(Theta(i-1)))
+muk*(Velocity(i-1))^2/radius);
Theta(i)= Theta(i-1)+dt/(2*radius)*(Velocity(i)+Velocity(i-1));
s(i)=s(i-1)+ dt*(Velocity(i)+Velocity(i-1))/2;
time(i)= u+(i-1)*dt;
end
v=sind(phi);
t=linspace(0,2,20);
Theta(i)=((Theta(i)+Theta(i-1))/2);
s2 = radius*Theta(i);
Theta(i) = Theta(i)*180/pi;
Velocity(i) = (Velocity(i)+Velocity(i-1))/2;
s(i) = (s(i)+s(i-1))/2;
% Printing the Results
disp(['Time = %5.4f sec\n',num2str((time(i)))])
disp(['Theta = %5.4f deg\n',num2str((Theta(i)))])
numel(time)
%
plot(t,v)
% v=sind(phi)
Hold on
syms mass acc grav angle(t)
% Mass of pendulum is given as 0.1
% acc is the acceleration
% grav is the gravitational forcc
% angle is the theta
equation1 = mass*acc == -mass*grav*sin(angle)
syms r
equation1 = subs(equation1,acc,r*diff(angle,2))
%eqn = isolate(eqn,diff(theta,2)) % isolating the angular acceleration
syms omeg_a
equation1 = subs(equation1,grav/r,omeg_a^2)
% linearizing the equations to solve them analyticcaly
syms exe
approx = taylor(sin(exe),exe,'Order',2);
8
EGB211 Computer lab assignment

approx = subs(approx,exe,angle(t))
%
eqnLinear = subs(equation1,sin(angle(t)),approx)
% solving the equation analytically
syms angle_0 angle_t0
angle_t = diff(angle);
cond_itions = [angle(0) == angle_0, angle_t(0) == angle_t0];
assume(omeg_a,'real')
thetaSol(t) = dsolve(eqnLinear,cond_itions)
%%
% PLOTING THE MOTION OF THE PENDULUM
grav_ity = 9.81; % gravity
ra_dius = 2; % length of the pendulum
omega_0_Val = sqrt(grav_ity/ra_dius);
T = 2*pi/omega_0_Val;
%setting the initial conditions
theta_0Val = 0.1*pi; % Solution only valid for small angles.
theta_t0Val = 0; % Initially at rest.
% substituting intial conditions and physical parameters
var_ables = [omeg_a angle_0 angle_t0];
val_ues = [omega_0_Val theta_0Val theta_t0Val];
angle_soln = subs(thetaSol,var_ables,val_ues);
% plotting tjhe harmonic motion
trew=angle_soln(t*T)/pi
%
fplot(trew, [0 5]);
grid on;
title('SPRING Pendulum graph');
xlabel('t/T');
ylabel('\theta/\pi');
hold off
9
EGB211 Computer lab assignment

Numerical Solution Application:
7. Based on the finite difference code in Question 4, develop a new code for bungee jump simulation. Use the
following set ups to adapt the code into the bungee system:
 When the distance between the person and the fixed end is less than the free
length of the cord, the person does free fall/ projectile motion.
 When the distance between the person and the fixed end is more than the free
length of the cord, the bungee cord applies the tension force and a damping
force: FB=T +FD =−k∗( L(t )−L0 )−5∗v y
 To avoid entanglement of the cord, the distance between the two ends of the
cord is x 0=2 m at the beginning.
 The mass of the cord can be ignored. The mass of the person M = 60 kg.
The elastic coefficient k = 20 N/m. The free length of the cord is L0 = 20 m.
The initial velocity of the person is 0.
1) Plot the trajectory of the person in the Cartesian coordinate in the first 60 seconds.
2) Find the minimum distance to the ground and the cliff for the person to bungee jump safely.
3) Show the velocity magnitude and acceleration magnitude history of the person in the first 60 seconds.
Hint: use if command in Matlab to switch between two equations of motions.
Answer within this box. Change the size of the box if needed.
%Goal: Model the Spring Pendulum in 3-D with RK4
format 'long'
M = 0.1; %Mass in kg
Grav = 9.81; %Gravity in m/s^2
k_spring = 20; %Spring constant in N/m
Length = 20; % rope length
omega_w = sqrt(k_spring/M); %Angular frequency of ossilations in rad/s
P=[3 1 -2.2]; % initial position matrix for x, y and z
x_p = 3; %Initial x-position
y_0 =P(:,2); %Initial y-position in m
z_p = P(:,3); %Initial z-position in m
vx_0 = .1; %Initial x-velocity in m/s
vy_p = .2; %Initial x-velocity in m/s
vz_0 = .3; %Initial x-velocity in m/s
delta_t = .001; %Time step in s
time = 20; %Total time to run simulation in s
%Vectors store positions and velocities
10
EGB211 Computer lab assignment

x_p = []; %Stores x-position
y_p = []; %Stores y-position
z_p = []; %Stores z-position
x_vel = []; %Stores x-velocity
y_vel = []; %Stores y-velocity
z_vel = []; %Stores z-velocity
r_pos = []; %Stores radial position
vel_city = []; %Stores total velocity
for i = 1:time/delta_t
rad_p = sqrt(P(:,1)^2 + P(:,2)^2 + z_p^2); %Radial position
%velocity in x direction
dir_vx = delta_t*(-omega_w^2*(1-Length/rad_p)*P(:,1));
dir_x2 = dir_vx;
dir_x3 = dir_vx;
dir_x4 = dir_vx;
v_xdir = vx_0 + (dir_vx + 2*dir_x2 + 2*dir_x3 + dir_x4)/6;
%Solves the y-velocity
dir_y1 = delta_t*(-omega_w^2*(1-Length/rad_p)*P(:,2));
dir_y2 = dir_y1;
dir_y3 = dir_y1;
dir_y4 = dir_y1;
dir_vy = vy_p + (dir_y1 + 2*dir_y2 + 2*dir_y3 + dir_y4)/6;
%Solves the z-velocity
dvz1 = delta_t*(-omega_w^2*(1-Length/rad_p)*z_p - Grav);
dvz2 = dvz1;
dvz3 = dvz1;
11
EGB211 Computer lab assignment

dvz4 = dvz1;
v_zdirection = vz_0 + (dvz1 + 2*dvz2 + 2*dvz3 + dvz4)/6;
%Solve the x-position
d_x1 = delta_t*vx_0;
dx2 = d_x1; dx3 = d_x1; dx4 = d_x1;
x_position = P(:,1) + (d_x1 + 2*dx2 + 2*dx3 + dx4)/6;
%Solve the y-position
y1_p = delta_t*vy_p;
p_y2 = y1_p;
p_y3 = y1_p;
p_y4 = y1_p;
y_pos = P(:,2) + (y1_p + 2*p_y2 + 2*p_y3 + p_y4)/6;
%Solve the z-position
d_z1 = delta_t*vz_0;
dz2 = d_z1;dz3 = d_z1;dz4 = d_z1;
z_position = z_p + (d_z1 + 2*dz2 + 2*dz3 + dz4)/6;
%Appends vectors to save all positions and velocities
x_p = [x_p,P(:,1)]; y_p = [y_p,P(:,2)];
z_p = [z_p,z_p];x_vel = [x_vel,vx_0];
y_vel = [y_vel,vy_p];z_vel = [z_vel,vz_0];
r_pos = [r_pos,rad_p];vel_city = [vel_city,sqrt(vx_0^2 + vy_p^2 + vz_0^2)];
%Set the current positions and velocities as the original to iterate.
x_p = x_position;y_0 = y_pos;
z_p = z_position;vx_0 = v_xdir;
12
EGB211 Computer lab assignment

vy_p = dir_vy;vz_0 = v_zdirection;
end
%period vs position
plot(1:time/delta_t,r_pos)
title('rposition against time)
13
EGB211 Computer lab assignment