Digital Control of DC Motor and PID Tuning
VerifiedAdded on 2021/04/17
|36
|6116
|114
AI Summary
The assignment involves designing and simulating a digital control system for a DC motor, including the implementation of a PID controller. The system is modeled in both continuous and discrete time domains, with the use of MATLAB scripts to perform calculations and simulations. The PID controller is designed using Ziegler-Nichols tuning method, and its effectiveness is tested through root locus analysis. The assignment also includes a discussion on the discretization of the system and the impact of sampling time on the system's performance.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

FACULTY OF ENGINEERING, ENVIRONMENT, AND COMPUTING
306SE CONTROL AND INSTRUMENTATION 2
TECHNICAL REPORT TITLE:
CONTINUOUS AND DISCRETE TIME PID CONTROL OF DC MOTOR APPLICATION
STUDENT NAME
STUDENT ID NUMBER
LECTURER: Dr. Nazmul Huda
Date of Submission
02nd July 2018
306SE CONTROL AND INSTRUMENTATION 2
TECHNICAL REPORT TITLE:
CONTINUOUS AND DISCRETE TIME PID CONTROL OF DC MOTOR APPLICATION
STUDENT NAME
STUDENT ID NUMBER
LECTURER: Dr. Nazmul Huda
Date of Submission
02nd July 2018
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

TABLE OF CONTENTS
SECTION I..................................................................................................................................................3
INTRODUCTION...................................................................................................................................3
THEORY OF PID CONTROL................................................................................................................7
TECHNOLOGY AND STATE OF THE ART PID CONTROL.............................................................9
MODERN ALTERNATIVES TO PID CONTROL FOR ELECTROMECHANICAL SYSTEMS......10
CONCLUSION.....................................................................................................................................10
FUTURE PROJECTIONS ON PID CONTROL...................................................................................11
SECTION II..............................................................................................................................................12
SECTION III.............................................................................................................................................24
REFERENCES..........................................................................................................................................33
1
SECTION I..................................................................................................................................................3
INTRODUCTION...................................................................................................................................3
THEORY OF PID CONTROL................................................................................................................7
TECHNOLOGY AND STATE OF THE ART PID CONTROL.............................................................9
MODERN ALTERNATIVES TO PID CONTROL FOR ELECTROMECHANICAL SYSTEMS......10
CONCLUSION.....................................................................................................................................10
FUTURE PROJECTIONS ON PID CONTROL...................................................................................11
SECTION II..............................................................................................................................................12
SECTION III.............................................................................................................................................24
REFERENCES..........................................................................................................................................33
1

LIST OF FIGURES
Figure 1 open loop block diagram system...................................................................................................4
Figure 2 The Burglar alarm system in an open loop system........................................................................4
Figure 3 Closed loop system with a unity feedback.....................................................................................5
Figure 4 Air Conditioner: Example of a closed loop control system...........................................................5
Figure 5 The Process flow diagram of the closed-loop system with PID controller....................................6
Figure 6 The PID controller components in parallel implementation in a control system...........................6
2
Figure 1 open loop block diagram system...................................................................................................4
Figure 2 The Burglar alarm system in an open loop system........................................................................4
Figure 3 Closed loop system with a unity feedback.....................................................................................5
Figure 4 Air Conditioner: Example of a closed loop control system...........................................................5
Figure 5 The Process flow diagram of the closed-loop system with PID controller....................................6
Figure 6 The PID controller components in parallel implementation in a control system...........................6
2

SECTION I
Pi and PID control overview and applications
INTRODUCTION
Control is crucial in industrial applications since it would be quite challenging to perform
the tasks as assigned to a machine accurately. The controls systems are meant to direct, instruct,
and regulate the tools and devices in the industries. The control systems are applied in
mechanical, automotive, electrical, and pneumatic systems. The mechanical systems, for
instance, need a control where the input and intended output are controlled. For all the aforesaid
different types of systems, there are two classifications in control engineering. The PID
controller finds application in chemical industries based on its rate of success in practical
applications of this nature. The systems can either be open-loop systems or closed-loop systems.
The systems are represented using block diagrams to show the processes and their
interaction with inputs and outputs. For an open-loop system, the information is fed into the plant
or system which performs processing, and the result or manufacturing is yielded. One typical
example is the washing machine. In the open loop system, the input and output are not related
such that in a washing machine, the efficiency of cleaning does not depend on the information
instead of the present time.
Figure 1 open loop block diagram system
3
Pi and PID control overview and applications
INTRODUCTION
Control is crucial in industrial applications since it would be quite challenging to perform
the tasks as assigned to a machine accurately. The controls systems are meant to direct, instruct,
and regulate the tools and devices in the industries. The control systems are applied in
mechanical, automotive, electrical, and pneumatic systems. The mechanical systems, for
instance, need a control where the input and intended output are controlled. For all the aforesaid
different types of systems, there are two classifications in control engineering. The PID
controller finds application in chemical industries based on its rate of success in practical
applications of this nature. The systems can either be open-loop systems or closed-loop systems.
The systems are represented using block diagrams to show the processes and their
interaction with inputs and outputs. For an open-loop system, the information is fed into the plant
or system which performs processing, and the result or manufacturing is yielded. One typical
example is the washing machine. In the open loop system, the input and output are not related
such that in a washing machine, the efficiency of cleaning does not depend on the information
instead of the present time.
Figure 1 open loop block diagram system
3
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Another typical example of the open loop system is the burglar alarm system. The system
operates by detecting motion or movement within the vicinity of a home using a sensor. Any
change recognized triggers an alarm. The alarm can only be stopped manually.
Figure 2 The Burglar alarm system in an open loop system
One critical caveat experienced with the open loop control system is the inability to make
automatic adjustments especially when the input changes. The free loop system is, therefore, not
suitable for use as a sophisticated control system in industrial applications. Some of the outputs
obtained may be of very high magnitude or even negligible magnitudes which could affect the
operation of systems. This call for a feedback loop to enable system control. The introduction of
a feedback loop in order makes the system a closed loop control system. The output of the
control system is used to adjust the input signal. The system compares the output with the
intended result, and it takes action to improve the input signal to ensure that the expected output
is obtained. The use of the feedback loop increases the accuracy of the production.
Figure 3 Closed loop system with a unity feedback
The feedback can either be positive or negative depending on the magnitude of the
output. The positive feedback seeks to make the yielded output deviates from the present
4
operates by detecting motion or movement within the vicinity of a home using a sensor. Any
change recognized triggers an alarm. The alarm can only be stopped manually.
Figure 2 The Burglar alarm system in an open loop system
One critical caveat experienced with the open loop control system is the inability to make
automatic adjustments especially when the input changes. The free loop system is, therefore, not
suitable for use as a sophisticated control system in industrial applications. Some of the outputs
obtained may be of very high magnitude or even negligible magnitudes which could affect the
operation of systems. This call for a feedback loop to enable system control. The introduction of
a feedback loop in order makes the system a closed loop control system. The output of the
control system is used to adjust the input signal. The system compares the output with the
intended result, and it takes action to improve the input signal to ensure that the expected output
is obtained. The use of the feedback loop increases the accuracy of the production.
Figure 3 Closed loop system with a unity feedback
The feedback can either be positive or negative depending on the magnitude of the
output. The positive feedback seeks to make the yielded output deviates from the present
4

command status while the negative feedback causes the new production to move closer towards
the current command status (Gu, et al., 2013). For instance, when an amplifier is put close to the
microphone, the input volume kept increasing hence the interference increased causing a lot of
noise pollution. The feedback loop may require the input reduced by moving the mic away from
the amplifier. The modern industrial applications have embraced the closed-loop control systems
as they need automation of the arrangements. Some of the conventional closed-loop system
applications are air conditioners, refrigerators, automatic rice cookers, electronic ticketing
machines. Due to the complexity of the systems, they are more expensive and complicated to
design. One typical example is the air conditioner,
Figure 4 Air Conditioner: Example of a closed loop control system
In the industrial applications, the PID controller is commonly implemented to provide control in
both small-scale and large-scale devices.
Figure 5 The Process flow diagram of the closed-loop system with PID controller
5
the current command status (Gu, et al., 2013). For instance, when an amplifier is put close to the
microphone, the input volume kept increasing hence the interference increased causing a lot of
noise pollution. The feedback loop may require the input reduced by moving the mic away from
the amplifier. The modern industrial applications have embraced the closed-loop control systems
as they need automation of the arrangements. Some of the conventional closed-loop system
applications are air conditioners, refrigerators, automatic rice cookers, electronic ticketing
machines. Due to the complexity of the systems, they are more expensive and complicated to
design. One typical example is the air conditioner,
Figure 4 Air Conditioner: Example of a closed loop control system
In the industrial applications, the PID controller is commonly implemented to provide control in
both small-scale and large-scale devices.
Figure 5 The Process flow diagram of the closed-loop system with PID controller
5

The proportional-integral-derivative controller is a control loop feedback mechanism.
The PID algorithm has three major components namely, the proportional component, the integral
part, and the derivative. Each element affects the output signal to get the optimal performance of
the system.
Figure 6 The PID controller components in parallel implementation in a control system
From the control system, the PID algorithm revolves around correcting the error. The
error is usually the difference between the process variable and the setpoint. Some drawbacks are
seen by the very high value of proportional control leads to the oscillation of the Process
variables. The controller tends to generate an offset value. These controllers increase the
maximum overshoot of the system. The yielded signal tends to have the offset minimized by the
essential part. The preceding section and the recent trajectory of the controller error have no
impact on the proportional term as it is.
The equivalent corrects instances of failure, the correct integral accumulation of failure,
and the derivative corrects the present error in respect to the error in the previous check. The
effect of the derivative is to counter the overshoot by the proportional and integral parts. When
6
The PID algorithm has three major components namely, the proportional component, the integral
part, and the derivative. Each element affects the output signal to get the optimal performance of
the system.
Figure 6 The PID controller components in parallel implementation in a control system
From the control system, the PID algorithm revolves around correcting the error. The
error is usually the difference between the process variable and the setpoint. Some drawbacks are
seen by the very high value of proportional control leads to the oscillation of the Process
variables. The controller tends to generate an offset value. These controllers increase the
maximum overshoot of the system. The yielded signal tends to have the offset minimized by the
essential part. The preceding section and the recent trajectory of the controller error have no
impact on the proportional term as it is.
The equivalent corrects instances of failure, the correct integral accumulation of failure,
and the derivative corrects the present error in respect to the error in the previous check. The
effect of the derivative is to counter the overshoot by the proportional and integral parts. When
6
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

the error is significant, the two coefficients affect the controller yield. The controller response
will imply a change in the error as fast as possible hence the need for a secondary function.
THEORY OF PID CONTROL
The algorithm of a PID controller is given as,
Unfortunately, further increase in the constant proportional causes a tendency to
oscillation. The effect of adding the integral component is that the strength of the integral action
increases with a decrease in integral time. The integral component deals with the steady state
error. The PI controller encounters oscillations, and the introduction of the second component
causes damping to increase. The damping of oscillations increases with increase in the derivative
time but decreases again when the derivative time becomes too large. The proportional response
is given as,
The proportional constant used need not be very high as it may result in the system
instability. Similarly, when the proportional gain is too low, the control action may tend to be
negligible hence fails to respond actively to the system disturbances. The proportional controller
has the effect of minimizing the rise time, and it may reduce the steady-state error but not
eliminate it. The commonly used value is such that the proportional band is expressed as a
percentage,
7
will imply a change in the error as fast as possible hence the need for a secondary function.
THEORY OF PID CONTROL
The algorithm of a PID controller is given as,
Unfortunately, further increase in the constant proportional causes a tendency to
oscillation. The effect of adding the integral component is that the strength of the integral action
increases with a decrease in integral time. The integral component deals with the steady state
error. The PI controller encounters oscillations, and the introduction of the second component
causes damping to increase. The damping of oscillations increases with increase in the derivative
time but decreases again when the derivative time becomes too large. The proportional response
is given as,
The proportional constant used need not be very high as it may result in the system
instability. Similarly, when the proportional gain is too low, the control action may tend to be
negligible hence fails to respond actively to the system disturbances. The proportional controller
has the effect of minimizing the rise time, and it may reduce the steady-state error but not
eliminate it. The commonly used value is such that the proportional band is expressed as a
percentage,
7

The integral controller has an impact on the magnitude of the error as well as the duration
of the failure. The fundamental is the sum of the instantaneous mistakes over a period. The
essential component eliminates the steady-state error, but it introduces the transient response and
worsens it. The comprehensive control is given as,
The secondary component is obtained by determining the slope of the error over a given
period and multiplying the value with the gain factor. The controller slows the rate of change of
the controller output. The controller has the effect of increasing the stability of the system, it
reduces the overshoot of the yielded output, and improves the transient response. It is given as,
The exact nonlinear dynamics of a humanoid with the constraint is derived as shown in the
equations below,
ω ( t ) =Ω
In the steady state,
Ra Ia+kb Ω=V s
T =k τ I a
8
of the failure. The fundamental is the sum of the instantaneous mistakes over a period. The
essential component eliminates the steady-state error, but it introduces the transient response and
worsens it. The comprehensive control is given as,
The secondary component is obtained by determining the slope of the error over a given
period and multiplying the value with the gain factor. The controller slows the rate of change of
the controller output. The controller has the effect of increasing the stability of the system, it
reduces the overshoot of the yielded output, and improves the transient response. It is given as,
The exact nonlinear dynamics of a humanoid with the constraint is derived as shown in the
equations below,
ω ( t ) =Ω
In the steady state,
Ra Ia+kb Ω=V s
T =k τ I a
8

There is a relationship observed between the input power, the external power, and the power
consumed through the resistor when the law of conservation of power is implemented such that,
I a V s=T Ω
Ra Ia
2=Resistance
V s Ia=T Ω+ Ra Ia
2
T =k b I a
V s ( t )=Ra ia (t ) + La∗d ia ( t )
dt +V b (t )
T M ( t ) =k ia ( t )
k =kT =k b
TECHNOLOGY AND STATE OF THE ART PID CONTROL
The linear system is linear if the output of the scaled sum of two input signals is the
equivalent scaled sum of outputs. The system is time-invariant if the system output is the same
and given the same input signal regardless of time. The system can be tuned using the different
tuning methods available. A new approach to the control of the electric drives with permanent
magnet synchronous motors, based on feedback linearization has been developed and
experimentally proven. Three various prescribed dynamics to speed demands were achieved.
The sampled data signal is a discrete time signal resulting from sampling a continuous
time signal. The digital signal is obtained by two processes of sampling and quantizing. The
9
consumed through the resistor when the law of conservation of power is implemented such that,
I a V s=T Ω
Ra Ia
2=Resistance
V s Ia=T Ω+ Ra Ia
2
T =k b I a
V s ( t )=Ra ia (t ) + La∗d ia ( t )
dt +V b (t )
T M ( t ) =k ia ( t )
k =kT =k b
TECHNOLOGY AND STATE OF THE ART PID CONTROL
The linear system is linear if the output of the scaled sum of two input signals is the
equivalent scaled sum of outputs. The system is time-invariant if the system output is the same
and given the same input signal regardless of time. The system can be tuned using the different
tuning methods available. A new approach to the control of the electric drives with permanent
magnet synchronous motors, based on feedback linearization has been developed and
experimentally proven. Three various prescribed dynamics to speed demands were achieved.
The sampled data signal is a discrete time signal resulting from sampling a continuous
time signal. The digital signal is obtained by two processes of sampling and quantizing. The
9
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

digital controls are used for achieving optimal performance in the form of maximum
productivity, maximum profit, minimum cost, and the use of minimum energy in production
activities. The advantages of the digital controls are that it has reduced price as there is the bulk
manufacturing of the control systems, they are flexible in response to design changes, noise
immunity, and they are more useful in the modern control systems. Some analog control systems
exhibit good performances as compared to the digital control systems. Digital control systems
tend to introduce a delay in the loop. The loop contains both analog and digital signals to provide
a means for conversion from one form to another to be used by each sub-system. The systems are
designed in the Z-domain. Hence, they must be converted from the S-domain to the Z-domain
for discretization of the control systems (Dougherty & Cooper, 2003).
MODERN ALTERNATIVES TO PID CONTROL FOR
ELECTROMECHANICAL SYSTEMS
The use of online optimization and advanced control. The new system allows for non-
linear systems to be controlled in the complex multi-variable interactions; operating constraints
are put in place such as safety limits, input saturation constraints, and product quality constraints.
The control over wide operating range are the process non-linearities and the changing process
parameters or conditions. The conventional approach is the multi-loop PI which is difficult to
tune. The ad-hoc constraint handling using logic programming and the lack of coordination. The
gain scheduling handles the non-linearity of systems. The use of multi-loop control in industrial
processes for multivariable and exhibit strong interaction among the variables. The stability of
the system is determined when the system has its characteristic equation to zero (Arbogast &
Dougherty, 2003).
10
productivity, maximum profit, minimum cost, and the use of minimum energy in production
activities. The advantages of the digital controls are that it has reduced price as there is the bulk
manufacturing of the control systems, they are flexible in response to design changes, noise
immunity, and they are more useful in the modern control systems. Some analog control systems
exhibit good performances as compared to the digital control systems. Digital control systems
tend to introduce a delay in the loop. The loop contains both analog and digital signals to provide
a means for conversion from one form to another to be used by each sub-system. The systems are
designed in the Z-domain. Hence, they must be converted from the S-domain to the Z-domain
for discretization of the control systems (Dougherty & Cooper, 2003).
MODERN ALTERNATIVES TO PID CONTROL FOR
ELECTROMECHANICAL SYSTEMS
The use of online optimization and advanced control. The new system allows for non-
linear systems to be controlled in the complex multi-variable interactions; operating constraints
are put in place such as safety limits, input saturation constraints, and product quality constraints.
The control over wide operating range are the process non-linearities and the changing process
parameters or conditions. The conventional approach is the multi-loop PI which is difficult to
tune. The ad-hoc constraint handling using logic programming and the lack of coordination. The
gain scheduling handles the non-linearity of systems. The use of multi-loop control in industrial
processes for multivariable and exhibit strong interaction among the variables. The stability of
the system is determined when the system has its characteristic equation to zero (Arbogast &
Dougherty, 2003).
10

CONCLUSION
In a nutshell, many industries are interested in controlling the temperature level of their
process tanks. The feedback loop of the PID measures the actual level of the parameter under
study and compares it to the input or reference value to determine the error. The PID controller
finds application in many industries and fields where process and plants have been installed.
There are new and alternative models for the implementation of the system. The digital PID
controllers are quite easy to implement and operate as they do not require a specialist or very
highly trained person to run. Other alternatives such as the pneumatic controller are applied for
the pneumatic system control to ensure that systems are controlled cost-effectively. According to
many researchers and practical tests carried out in the industry, it is recommended that the PID
controller is utilized for processes with low to medium order plant transfer functions with small
time delays.
FUTURE PROJECTIONS ON PID CONTROL
The conventional control scheme has multiple single inputs and single output PID
controllers used for the control of plants. The consequence of loop interaction is the lack of
coordination between different PID loops. Neighboring PID loops can cooperate with each other
or end up opposing or disturbing each other. Such advanced control systems can be used to solve
the Tennessee Eastman problem. The model predictive control does multivariable control based
on the on-line use of the dynamic model. The modified form of classical optimal control problem
can systematically and optimally handle multivariable interactions, operating input and output
constraints, and process non-linearities. Another approach is the use of the data-driven models.
The development of linear state space and transfer models starting from the first principles or
gray box models is quite an abstract proposition.
11
In a nutshell, many industries are interested in controlling the temperature level of their
process tanks. The feedback loop of the PID measures the actual level of the parameter under
study and compares it to the input or reference value to determine the error. The PID controller
finds application in many industries and fields where process and plants have been installed.
There are new and alternative models for the implementation of the system. The digital PID
controllers are quite easy to implement and operate as they do not require a specialist or very
highly trained person to run. Other alternatives such as the pneumatic controller are applied for
the pneumatic system control to ensure that systems are controlled cost-effectively. According to
many researchers and practical tests carried out in the industry, it is recommended that the PID
controller is utilized for processes with low to medium order plant transfer functions with small
time delays.
FUTURE PROJECTIONS ON PID CONTROL
The conventional control scheme has multiple single inputs and single output PID
controllers used for the control of plants. The consequence of loop interaction is the lack of
coordination between different PID loops. Neighboring PID loops can cooperate with each other
or end up opposing or disturbing each other. Such advanced control systems can be used to solve
the Tennessee Eastman problem. The model predictive control does multivariable control based
on the on-line use of the dynamic model. The modified form of classical optimal control problem
can systematically and optimally handle multivariable interactions, operating input and output
constraints, and process non-linearities. Another approach is the use of the data-driven models.
The development of linear state space and transfer models starting from the first principles or
gray box models is quite an abstract proposition.
11

The Research and Development control sections have focused on the application of the
new approach to enhance the control systems for the outer loop based on MRAC or SMC to
improve the precision of control. The discrete time signals are defined only at specific time
instances. The discrete time signals have amplitudes between two consecutive time instants
which is not determined but only on the particular time instance.
SECTION II
Shaft position of a DC motor
(i) Electrical and mechanical equations for the system
The DC motor electrical-mechanical equivalent circuit is as illustrated below,
12
new approach to enhance the control systems for the outer loop based on MRAC or SMC to
improve the precision of control. The discrete time signals are defined only at specific time
instances. The discrete time signals have amplitudes between two consecutive time instants
which is not determined but only on the particular time instance.
SECTION II
Shaft position of a DC motor
(i) Electrical and mechanical equations for the system
The DC motor electrical-mechanical equivalent circuit is as illustrated below,
12
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

The system introduces a back electromotive force at the armature section. The back
electromotive force is directly proportional to the angular velocity of the rotor within
the motor section. The motor generates a torque which is linearly related to the
armature current. It is given that at constant input voltage, the armature current and
the angular velocity and torque are constant.
The mechanical behavior of the systems is further analyzed using the equation,
The equations demonstrate the dynamic nature of the DC motor. When the electrical
term is neglected, the magnitude of the system reduces as the mechanical time
constant is left in the equation as the governing factor,
13
electromotive force is directly proportional to the angular velocity of the rotor within
the motor section. The motor generates a torque which is linearly related to the
armature current. It is given that at constant input voltage, the armature current and
the angular velocity and torque are constant.
The mechanical behavior of the systems is further analyzed using the equation,
The equations demonstrate the dynamic nature of the DC motor. When the electrical
term is neglected, the magnitude of the system reduces as the mechanical time
constant is left in the equation as the governing factor,
13

When the equation for armature current is substituted to the mechanical equation, we
obtain,
Having obtained the mechanical and electrical system functions for the DC motor, the
transfer function of the system can be obtained as,
Two external forces come to affect the system namely the input voltage and the
generated torque at the armature. These two forces tend to exhibit linear
proportionality such that,
The back emf, e, is proportional to the angular velocity of the shaft by a constant
factor.
The Laplace transform of the system equation is given as,
14
obtain,
Having obtained the mechanical and electrical system functions for the DC motor, the
transfer function of the system can be obtained as,
Two external forces come to affect the system namely the input voltage and the
generated torque at the armature. These two forces tend to exhibit linear
proportionality such that,
The back emf, e, is proportional to the angular velocity of the shaft by a constant
factor.
The Laplace transform of the system equation is given as,
14

The open loop transfer function is obtained by eliminating the electrical component
from the two equations. The rotational speed is considered as the output, and the
armature voltage is regarded as the input,
(ii) System transfer function & root-locus analysis
The system transfer function is given as,
G( s)= Kt
( Js +b ) ( Ls+ R )+ Kt Ke
Replacing with values,
G ( s ) = 0.02
( 0.3 s +0.02 ) ( 0.3 s+ 2 ) + 0.022
G ( s )= 0.02
( 0.09 s2 +0.18 s +0.04 ) +0 .0004
15
from the two equations. The rotational speed is considered as the output, and the
armature voltage is regarded as the input,
(ii) System transfer function & root-locus analysis
The system transfer function is given as,
G( s)= Kt
( Js +b ) ( Ls+ R )+ Kt Ke
Replacing with values,
G ( s ) = 0.02
( 0.3 s +0.02 ) ( 0.3 s+ 2 ) + 0.022
G ( s )= 0.02
( 0.09 s2 +0.18 s +0.04 ) +0 .0004
15
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
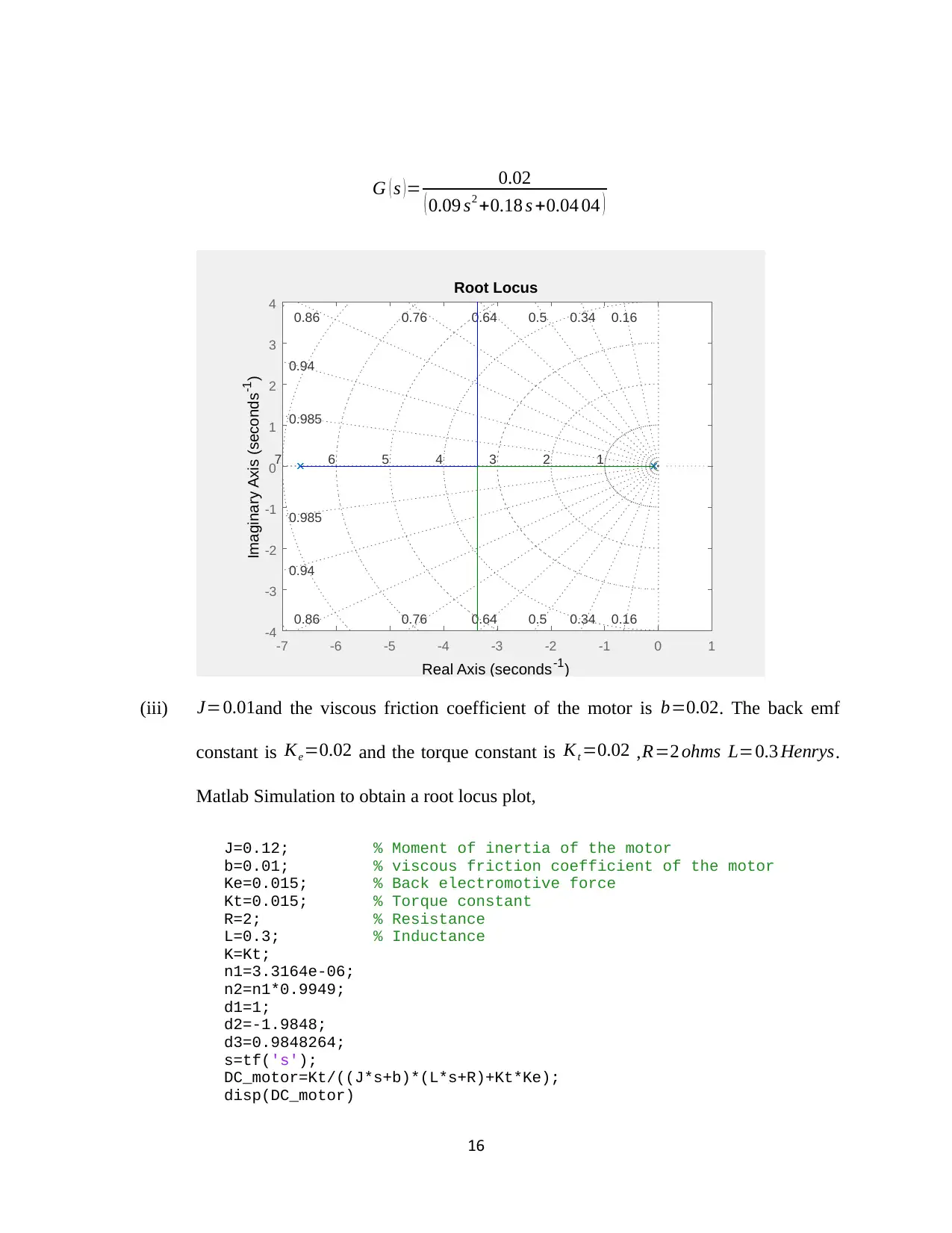
G ( s )= 0.02
( 0.09 s2 +0.18 s +0.04 04 )
-7 -6 -5 -4 -3 -2 -1 0 1
-4
-3
-2
-1
0
1
2
3
4
0.985
0.160.340.50.640.760.86
0.94
0.985
0.160.340.50.640.760.86
0.94
1234567
Root Locus
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
(iii) J=0.01and the viscous friction coefficient of the motor is b=0.02. The back emf
constant is Ke=0.02 and the torque constant is Kt =0.02 , R=2 ohms L=0.3 Henrys.
Matlab Simulation to obtain a root locus plot,
J=0.12; % Moment of inertia of the motor
b=0.01; % viscous friction coefficient of the motor
Ke=0.015; % Back electromotive force
Kt=0.015; % Torque constant
R=2; % Resistance
L=0.3; % Inductance
K=Kt;
n1=3.3164e-06;
n2=n1*0.9949;
d1=1;
d2=-1.9848;
d3=0.9848264;
s=tf('s');
DC_motor=Kt/((J*s+b)*(L*s+R)+Kt*Ke);
disp(DC_motor)
16
( 0.09 s2 +0.18 s +0.04 04 )
-7 -6 -5 -4 -3 -2 -1 0 1
-4
-3
-2
-1
0
1
2
3
4
0.985
0.160.340.50.640.760.86
0.94
0.985
0.160.340.50.640.760.86
0.94
1234567
Root Locus
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
(iii) J=0.01and the viscous friction coefficient of the motor is b=0.02. The back emf
constant is Ke=0.02 and the torque constant is Kt =0.02 , R=2 ohms L=0.3 Henrys.
Matlab Simulation to obtain a root locus plot,
J=0.12; % Moment of inertia of the motor
b=0.01; % viscous friction coefficient of the motor
Ke=0.015; % Back electromotive force
Kt=0.015; % Torque constant
R=2; % Resistance
L=0.3; % Inductance
K=Kt;
n1=3.3164e-06;
n2=n1*0.9949;
d1=1;
d2=-1.9848;
d3=0.9848264;
s=tf('s');
DC_motor=Kt/((J*s+b)*(L*s+R)+Kt*Ke);
disp(DC_motor)
16

%% displaying the state space
A=[-b/J K/J
-K/J -R/J];
B=[0
1/L];
C=[1 0];
D=0;
motor_ss=ss(A,B,C,D)
%% drawing the open loop root locus of the DC motor System
rlocus(DC_motor)
grid on
solution
motor_ss =
A =
x1 x2
x1 -0.08333 0.125
x2 -0.125 -16.67
B =
u1
x1 0
x2 3.333
C =
x1 x2
y1 1 0
D =
u1
y1 0
Continuous-time state-space model.
17
A=[-b/J K/J
-K/J -R/J];
B=[0
1/L];
C=[1 0];
D=0;
motor_ss=ss(A,B,C,D)
%% drawing the open loop root locus of the DC motor System
rlocus(DC_motor)
grid on
solution
motor_ss =
A =
x1 x2
x1 -0.08333 0.125
x2 -0.125 -16.67
B =
u1
x1 0
x2 3.333
C =
x1 x2
y1 1 0
D =
u1
y1 0
Continuous-time state-space model.
17
-7 -6 -5 -4 -3 -2 -1 0 1
-4
-3
-2
-1
0
1
2
3
4
0.985
0.160.340.50.640.760.86
0.94
0.985
0.160.340.50.640.760.86
0.94
1234567
Root Locus
Real Axis (seconds-1 )
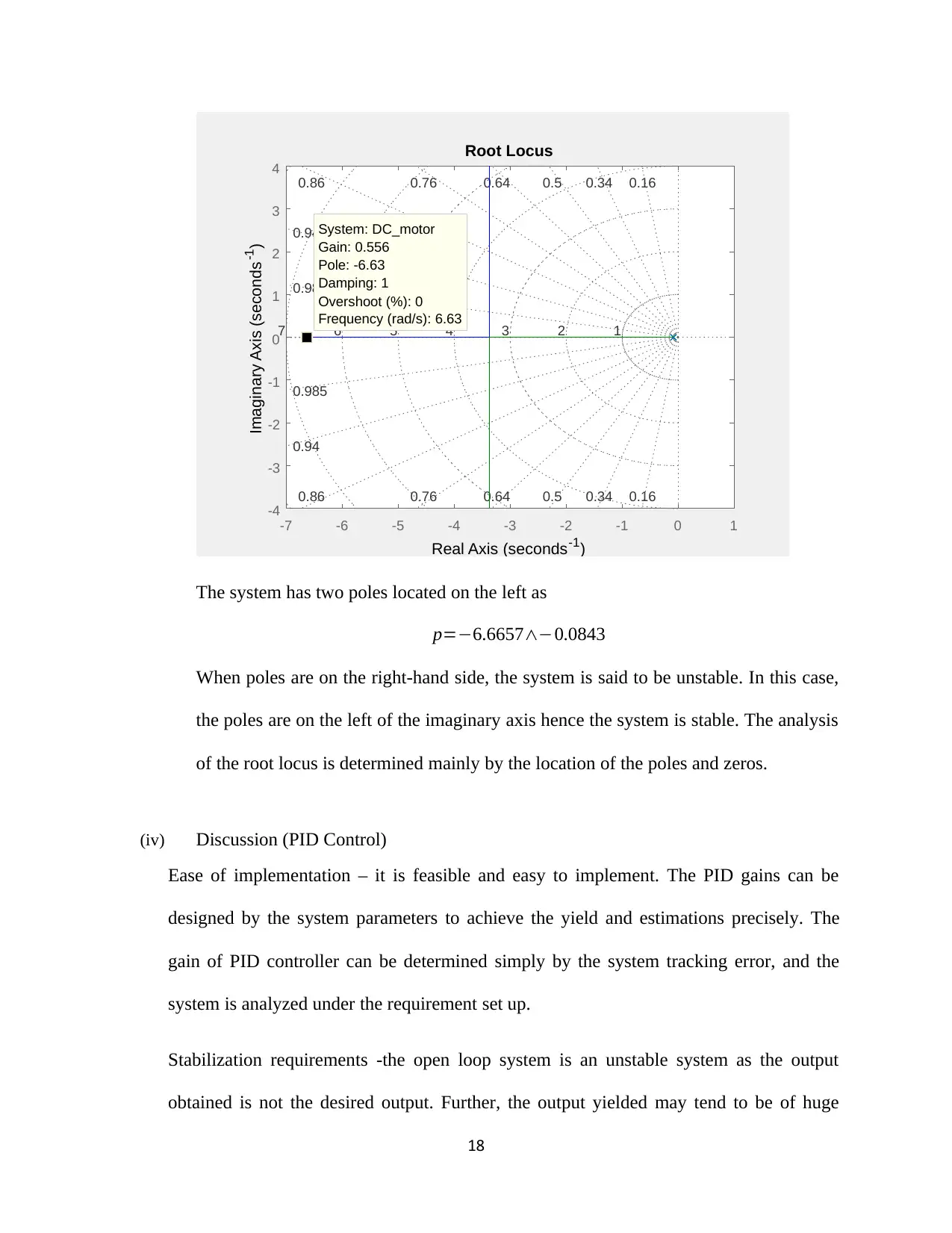
Imaginary Axis (seconds -1 ) System: DC_motor
Gain: 0.556
Pole: -6.63
Damping: 1
Overshoot (%): 0
Frequency (rad/s): 6.63
The system has two poles located on the left as
p=−6.6657∧−0.0843
When poles are on the right-hand side, the system is said to be unstable. In this case,
the poles are on the left of the imaginary axis hence the system is stable. The analysis
of the root locus is determined mainly by the location of the poles and zeros.
(iv) Discussion (PID Control)
Ease of implementation – it is feasible and easy to implement. The PID gains can be
designed by the system parameters to achieve the yield and estimations precisely. The
gain of PID controller can be determined simply by the system tracking error, and the
system is analyzed under the requirement set up.
Stabilization requirements -the open loop system is an unstable system as the output
obtained is not the desired output. Further, the output yielded may tend to be of huge
18
-4
-3
-2
-1
0
1
2
3
4
0.985
0.160.340.50.640.760.86
0.94
0.985
0.160.340.50.640.760.86
0.94
1234567
Root Locus
Real Axis (seconds-1 )
Imaginary Axis (seconds -1 ) System: DC_motor
Gain: 0.556
Pole: -6.63
Damping: 1
Overshoot (%): 0
Frequency (rad/s): 6.63
The system has two poles located on the left as
p=−6.6657∧−0.0843
When poles are on the right-hand side, the system is said to be unstable. In this case,
the poles are on the left of the imaginary axis hence the system is stable. The analysis
of the root locus is determined mainly by the location of the poles and zeros.
(iv) Discussion (PID Control)
Ease of implementation – it is feasible and easy to implement. The PID gains can be
designed by the system parameters to achieve the yield and estimations precisely. The
gain of PID controller can be determined simply by the system tracking error, and the
system is analyzed under the requirement set up.
Stabilization requirements -the open loop system is an unstable system as the output
obtained is not the desired output. Further, the output yielded may tend to be of huge
18
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

magnitude hence destroying the cascaded sub-sections attached to the output. The control
system corrects the magnitude by ensuring the output provided is corrected until it is
achieved as the desired yield.
Performance – the closed-loop control system guarantees that the efficiency of the system
is attained to close to an ideal value. The performance of a system is tested based on the
output obtained. The system is tested on may scale, and it should perform well and ensure
that the system parameters are stable all through.
Robustness – a system is considered robust when it can accommodate the uncertainties
and disturbances in the surrounding. The system may not be in a position to resist the
noises and hence depict low robustness as demonstrated in the open-loop systems. The
PID may have a low robust ability compare to some of the modern alternatives of the PID
used in the various industrial applications. The robust controllers enable the system to
encounter the challenges of operating in a very dynamic uncertain environment in the
industrial sector. Some of the environmental disturbances are weather changes,
temperature variations, and especially power fluctuations such as the power surge
(Arbogast & Dougherty, 2003).
Energy consumption – as much as an industry wishes to automate their processes and
plants, there is need to consider the consumption of energy by the equipment installed.
The open loop does not consider the energy consumed or even regulate it; rather it
follows the initial settings. For instance, when using an air conditioner, the system should
detect temperature changes and change modes when suitable to reduce the energy
consumption levels.
19
system corrects the magnitude by ensuring the output provided is corrected until it is
achieved as the desired yield.
Performance – the closed-loop control system guarantees that the efficiency of the system
is attained to close to an ideal value. The performance of a system is tested based on the
output obtained. The system is tested on may scale, and it should perform well and ensure
that the system parameters are stable all through.
Robustness – a system is considered robust when it can accommodate the uncertainties
and disturbances in the surrounding. The system may not be in a position to resist the
noises and hence depict low robustness as demonstrated in the open-loop systems. The
PID may have a low robust ability compare to some of the modern alternatives of the PID
used in the various industrial applications. The robust controllers enable the system to
encounter the challenges of operating in a very dynamic uncertain environment in the
industrial sector. Some of the environmental disturbances are weather changes,
temperature variations, and especially power fluctuations such as the power surge
(Arbogast & Dougherty, 2003).
Energy consumption – as much as an industry wishes to automate their processes and
plants, there is need to consider the consumption of energy by the equipment installed.
The open loop does not consider the energy consumed or even regulate it; rather it
follows the initial settings. For instance, when using an air conditioner, the system should
detect temperature changes and change modes when suitable to reduce the energy
consumption levels.
19

Steady state error – the actuators can saturate and hence the error continues to
accumulate. When the controller regains control, the response may end up being
exaggerated. The proportional controller minimizes the steady-state error in the system,
but the introduction of the integral component eliminates the effects of the steady state
error in the plant.
(v) Ziegler Nichols PID tuning method (MATLAB implementation)
In practice, when the Ziegler-Nichols tuning is implemented in an industrial plant the
system transfer function of the plant is unknown to the control engineers. The control
engineers are required to fine tune the device a little bit to attain the appropriate control
for the system. The system plant, G(s), is a second order system that has a lag and
integration for its transfer function. There are some tuning methods used in controlling
system plants such as:
(i) Ziegler-Nichols open loop method (yields low results for percent
overshoot)
(ii) CHR method for 0% overshoot
(iii) Ziegler-Nichols closed-loop method (Has a shorter settling time)
20
accumulate. When the controller regains control, the response may end up being
exaggerated. The proportional controller minimizes the steady-state error in the system,
but the introduction of the integral component eliminates the effects of the steady state
error in the plant.
(v) Ziegler Nichols PID tuning method (MATLAB implementation)
In practice, when the Ziegler-Nichols tuning is implemented in an industrial plant the
system transfer function of the plant is unknown to the control engineers. The control
engineers are required to fine tune the device a little bit to attain the appropriate control
for the system. The system plant, G(s), is a second order system that has a lag and
integration for its transfer function. There are some tuning methods used in controlling
system plants such as:
(i) Ziegler-Nichols open loop method (yields low results for percent
overshoot)
(ii) CHR method for 0% overshoot
(iii) Ziegler-Nichols closed-loop method (Has a shorter settling time)
20
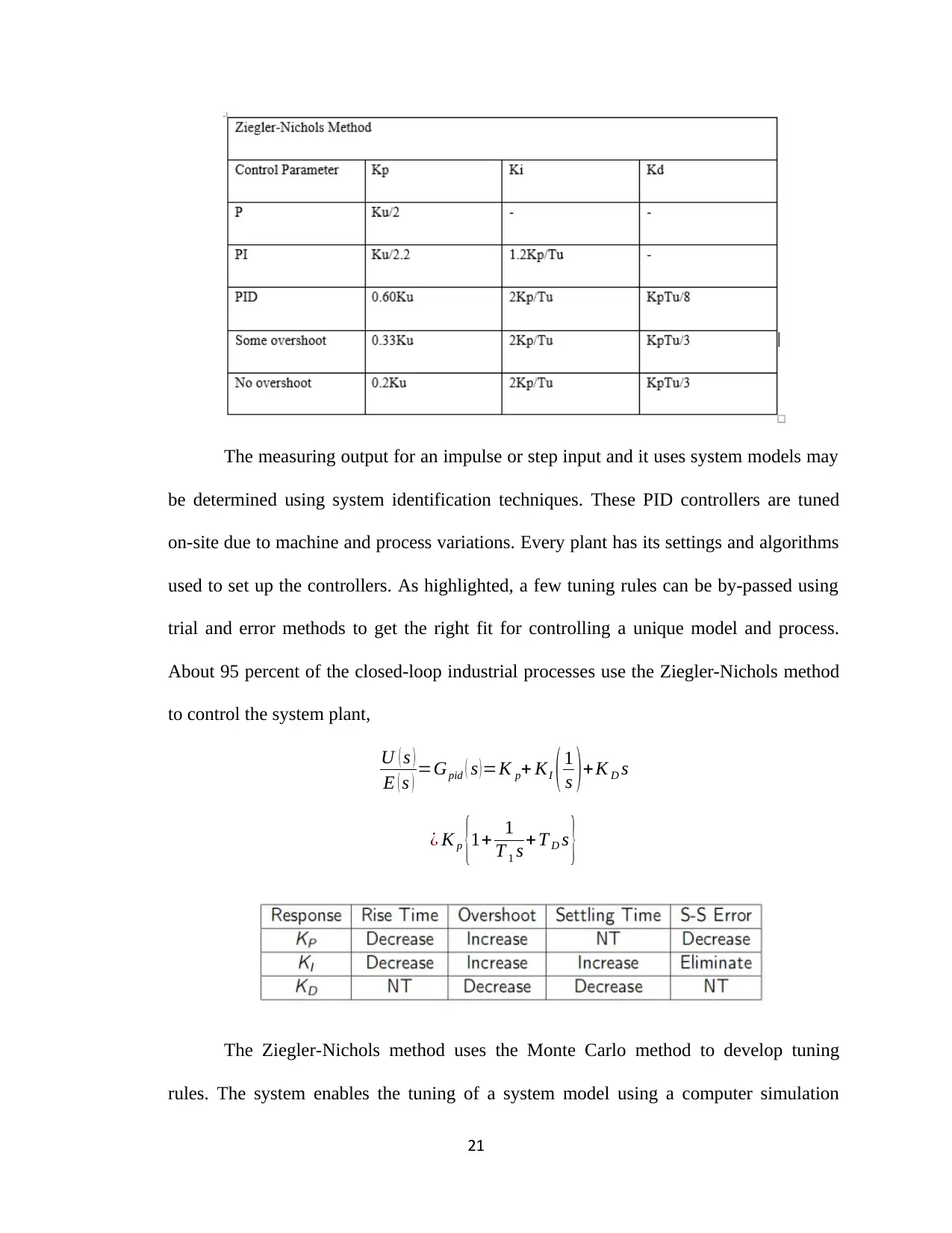
The measuring output for an impulse or step input and it uses system models may
be determined using system identification techniques. These PID controllers are tuned
on-site due to machine and process variations. Every plant has its settings and algorithms
used to set up the controllers. As highlighted, a few tuning rules can be by-passed using
trial and error methods to get the right fit for controlling a unique model and process.
About 95 percent of the closed-loop industrial processes use the Ziegler-Nichols method
to control the system plant,
U ( s )
E ( s ) =Gpid ( s )=K p+ KI ( 1
s )+K D s
¿ K p {1+ 1
T 1 s + T D s }
The Ziegler-Nichols method uses the Monte Carlo method to develop tuning
rules. The system enables the tuning of a system model using a computer simulation
21
be determined using system identification techniques. These PID controllers are tuned
on-site due to machine and process variations. Every plant has its settings and algorithms
used to set up the controllers. As highlighted, a few tuning rules can be by-passed using
trial and error methods to get the right fit for controlling a unique model and process.
About 95 percent of the closed-loop industrial processes use the Ziegler-Nichols method
to control the system plant,
U ( s )
E ( s ) =Gpid ( s )=K p+ KI ( 1
s )+K D s
¿ K p {1+ 1
T 1 s + T D s }
The Ziegler-Nichols method uses the Monte Carlo method to develop tuning
rules. The system enables the tuning of a system model using a computer simulation
21
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

system or a digital input point when the specific transfer function of the system and
controller is not known to the engineer. A number of the industrial processes are non-
linear and dynamic as a result of exposure to external noises. The introduction of external
disturbances makes the system quite difficult to work with. An alternative method
implemented is the good gain method. The method is obtained from a series of laboratory
experiments. When compared to the Ziegler-Nichols closed loop method, it does not
require the control system to be brought into sustained oscillations in the tuning phase.
Unlike the Nichols tuning method which is implemented on the PID controllers, the good
gain method is used in PI controllers.
wp=DC_motor; % system plant function
kp=input('Enter the Proportional constant (Kp)')
ki=input('Enter the Integral constant (Ki)')
kd=input('Enter the Derivative constant(Kd)')
s=tf('s')
Wc=kp*(1+(1/(ki*s))+kd*s) %Ziegler Nichols PID tuning Method
%for a closed loop implementation
sys_2=feedback(series(wp,Wc),1) %unity feedback
rlocus(sys_2)
grid on
p1=pole(sys_2)
22
controller is not known to the engineer. A number of the industrial processes are non-
linear and dynamic as a result of exposure to external noises. The introduction of external
disturbances makes the system quite difficult to work with. An alternative method
implemented is the good gain method. The method is obtained from a series of laboratory
experiments. When compared to the Ziegler-Nichols closed loop method, it does not
require the control system to be brought into sustained oscillations in the tuning phase.
Unlike the Nichols tuning method which is implemented on the PID controllers, the good
gain method is used in PI controllers.
wp=DC_motor; % system plant function
kp=input('Enter the Proportional constant (Kp)')
ki=input('Enter the Integral constant (Ki)')
kd=input('Enter the Derivative constant(Kd)')
s=tf('s')
Wc=kp*(1+(1/(ki*s))+kd*s) %Ziegler Nichols PID tuning Method
%for a closed loop implementation
sys_2=feedback(series(wp,Wc),1) %unity feedback
rlocus(sys_2)
grid on
p1=pole(sys_2)
22
-18 -16 -14 -12 -10 -8 -6 -4 -2 0 2
-1.5
-1
-0.5
0
0.5
1
1.5
0.996
0.750.920.9660.9840.9920.996
0.998
1
0.750.920.9660.9840.992
0.998
1
24681012141618
Root Locus
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
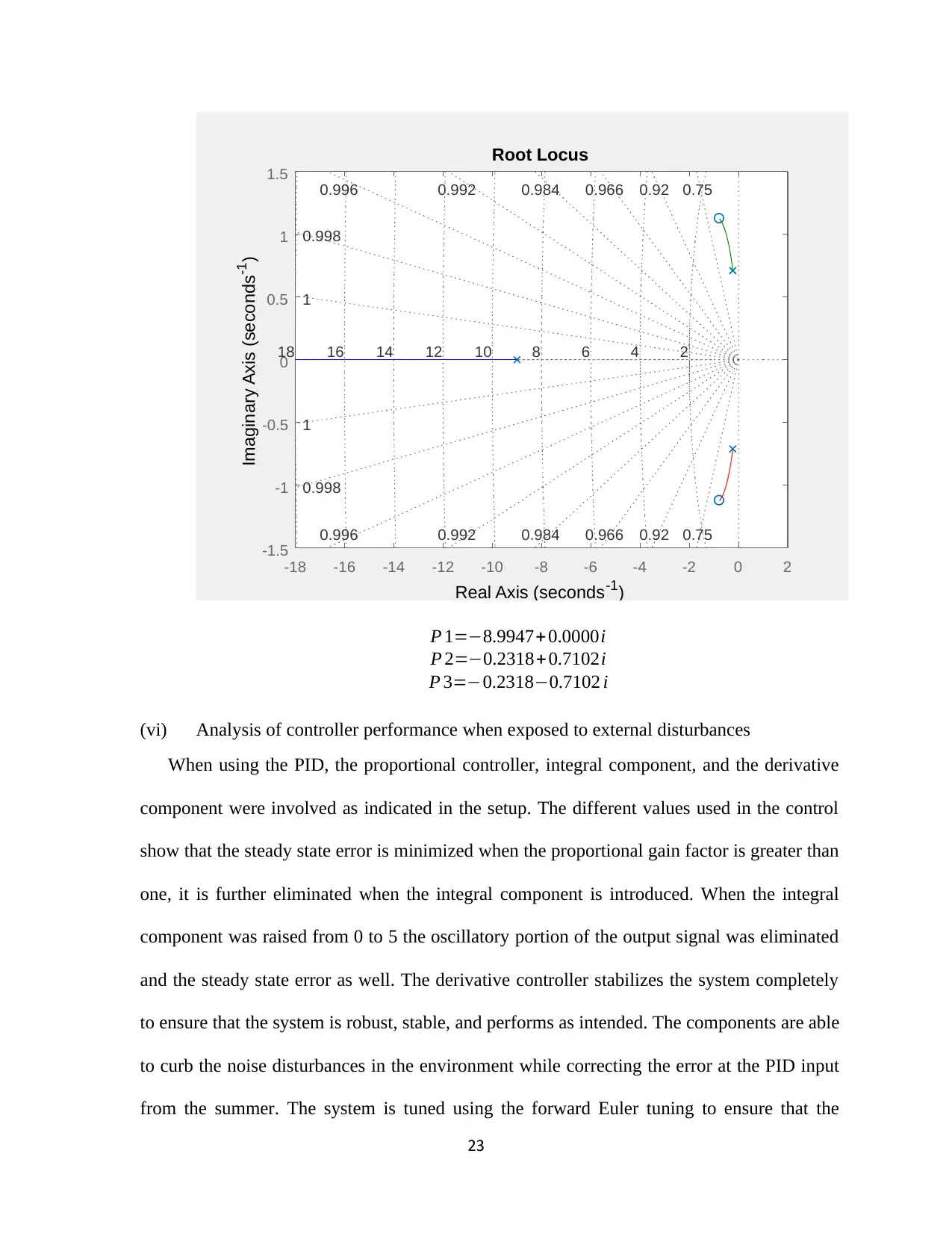
P 1=−8.9947+ 0.0000i
P 2=−0.2318+0.7102i
P 3=−0.2318−0.7102 i
(vi) Analysis of controller performance when exposed to external disturbances
When using the PID, the proportional controller, integral component, and the derivative
component were involved as indicated in the setup. The different values used in the control
show that the steady state error is minimized when the proportional gain factor is greater than
one, it is further eliminated when the integral component is introduced. When the integral
component was raised from 0 to 5 the oscillatory portion of the output signal was eliminated
and the steady state error as well. The derivative controller stabilizes the system completely
to ensure that the system is robust, stable, and performs as intended. The components are able
to curb the noise disturbances in the environment while correcting the error at the PID input
from the summer. The system is tuned using the forward Euler tuning to ensure that the
23
-1.5
-1
-0.5
0
0.5
1
1.5
0.996
0.750.920.9660.9840.9920.996
0.998
1
0.750.920.9660.9840.992
0.998
1
24681012141618
Root Locus
Real Axis (seconds-1)
Imaginary Axis (seconds-1)
P 1=−8.9947+ 0.0000i
P 2=−0.2318+0.7102i
P 3=−0.2318−0.7102 i
(vi) Analysis of controller performance when exposed to external disturbances
When using the PID, the proportional controller, integral component, and the derivative
component were involved as indicated in the setup. The different values used in the control
show that the steady state error is minimized when the proportional gain factor is greater than
one, it is further eliminated when the integral component is introduced. When the integral
component was raised from 0 to 5 the oscillatory portion of the output signal was eliminated
and the steady state error as well. The derivative controller stabilizes the system completely
to ensure that the system is robust, stable, and performs as intended. The components are able
to curb the noise disturbances in the environment while correcting the error at the PID input
from the summer. The system is tuned using the forward Euler tuning to ensure that the
23

component values set are in line with the required values to ensure stability of a system. It
was observed that a very large value on the proportional gain factor may cause more damage
than good as the signal tends to increase in magnitude to very high levels. The integral value
seeks to stabilize this by eliminating the steady state error. The Ziegler-Nichols method is
used in the plants with neither the integrators nor the dominant complex-conjugates poles.
The unit step response models an S-shaped curve or the reaction curve. The tuning method
use the gain estimator chart to determine the reaction of the different controller modes,
All controllers seek to solve two problems: faster responses imply poor system stability while
the better system stability states are only attained when the response is slow. The control
systems aim at reaching a compromise where there is acceptable stability and medium
fastness of response. The Ziegler-Nichols method is implemented in the following transfer
function models for different levels of systems,
24
was observed that a very large value on the proportional gain factor may cause more damage
than good as the signal tends to increase in magnitude to very high levels. The integral value
seeks to stabilize this by eliminating the steady state error. The Ziegler-Nichols method is
used in the plants with neither the integrators nor the dominant complex-conjugates poles.
The unit step response models an S-shaped curve or the reaction curve. The tuning method
use the gain estimator chart to determine the reaction of the different controller modes,
All controllers seek to solve two problems: faster responses imply poor system stability while
the better system stability states are only attained when the response is slow. The control
systems aim at reaching a compromise where there is acceptable stability and medium
fastness of response. The Ziegler-Nichols method is implemented in the following transfer
function models for different levels of systems,
24
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Another alternative method is the Tyreus-Luyben method. It is implemented like the Ziegler-
Nichols method but has different final controller settings. The controllers are implemented
for the PI and the PID controllers unlike the Ziegler-Nichols method which is suitable for
PID controllers solely. The controller setting for the Tyreus-Luyben method are,
Another method was proposed by Chien, Hrones, and Reswich is the CHR method which
modifies the Ziegler-Nichols open-loop method. It achieves a very quick response with or
without 20 percent overshoot in the output signal. To use this model, it is required that the
engineer or designer determines the first order and the dead time model of the system. To
achieve the faster response with very low overshoot, the proportional gain constant and the
derivative time is less while the integral component time is larger such that the integral action
is amplified over the proportional and the derivative. The later components are responsible
for reducing steady-state error and rise time respectively.
SECTION III
(i) Discretized system. Matlab for open and closed loop z-domain transfer functions.
The first step is to convert the system from continuous to discrete mode. The
analysis of the system can, after that, be done in the discrete mode. There are analog
and digital controllers implemented in series with the industrial plants or processes.
The digital controllers are being used more than the analog ones in the modern age.
There are several advantages of the digital controls such as the reduced costs in the
bulk manufacturing of the controller equipment. These controllers tend to be very
25
Nichols method but has different final controller settings. The controllers are implemented
for the PI and the PID controllers unlike the Ziegler-Nichols method which is suitable for
PID controllers solely. The controller setting for the Tyreus-Luyben method are,
Another method was proposed by Chien, Hrones, and Reswich is the CHR method which
modifies the Ziegler-Nichols open-loop method. It achieves a very quick response with or
without 20 percent overshoot in the output signal. To use this model, it is required that the
engineer or designer determines the first order and the dead time model of the system. To
achieve the faster response with very low overshoot, the proportional gain constant and the
derivative time is less while the integral component time is larger such that the integral action
is amplified over the proportional and the derivative. The later components are responsible
for reducing steady-state error and rise time respectively.
SECTION III
(i) Discretized system. Matlab for open and closed loop z-domain transfer functions.
The first step is to convert the system from continuous to discrete mode. The
analysis of the system can, after that, be done in the discrete mode. There are analog
and digital controllers implemented in series with the industrial plants or processes.
The digital controllers are being used more than the analog ones in the modern age.
There are several advantages of the digital controls such as the reduced costs in the
bulk manufacturing of the controller equipment. These controllers tend to be very
25

flexible in response to the design changes, noise immunity, and they are more useful
in the modern control systems. Some of the analog controllers tend to exhibit very
good performance as compared to the digital controllers. The systems that utilize the
digital controllers are designed in the z-domain. Hence, they must be converted from
the continuous time domain or the s-domain to the discrete time domain or z domain.
Solution
Zpk(DC_motor) =
0.41667
---------------------
(s+6.666) (s+0.08428)
Continuous-time zero/pole/gain model.
Zpk(DP_motor) =
2.0787e-07 (z+0.9978)
---------------------
(z-1) (z-0.9934)
Sample time: 0.001 seconds
Discrete-time zero/pole/gain model.
p 2=0.9999∧0.993 4
26
in the modern control systems. Some of the analog controllers tend to exhibit very
good performance as compared to the digital controllers. The systems that utilize the
digital controllers are designed in the z-domain. Hence, they must be converted from
the continuous time domain or the s-domain to the discrete time domain or z domain.
Solution
Zpk(DC_motor) =
0.41667
---------------------
(s+6.666) (s+0.08428)
Continuous-time zero/pole/gain model.
Zpk(DP_motor) =
2.0787e-07 (z+0.9978)
---------------------
(z-1) (z-0.9934)
Sample time: 0.001 seconds
Discrete-time zero/pole/gain model.
p 2=0.9999∧0.993 4
26

(ii) Root locus analysis of the discretized system in the z-domain.
When the sampling time is set to t=0.01 seconds
-7 -6 -5 -4 -3 -2 -1 0 1 2
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T0.5 /T0.6 /T
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T0.5 /T0.6 /T
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Root Locus
Real Axis
Imaginary Axis
Solutions
answer =
0.41667
---------------------
(s+6.666) (s+0.08428)
Continuous-time zero/pole/gain model.
answer =
2.0372e-05 (z+0.9778)
---------------------
(z-0.9992) (z-0.9355)
27
When the sampling time is set to t=0.01 seconds
-7 -6 -5 -4 -3 -2 -1 0 1 2
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T0.5 /T0.6 /T
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T0.5 /T0.6 /T
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Root Locus
Real Axis
Imaginary Axis
Solutions
answer =
0.41667
---------------------
(s+6.666) (s+0.08428)
Continuous-time zero/pole/gain model.
answer =
2.0372e-05 (z+0.9778)
---------------------
(z-0.9992) (z-0.9355)
27
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
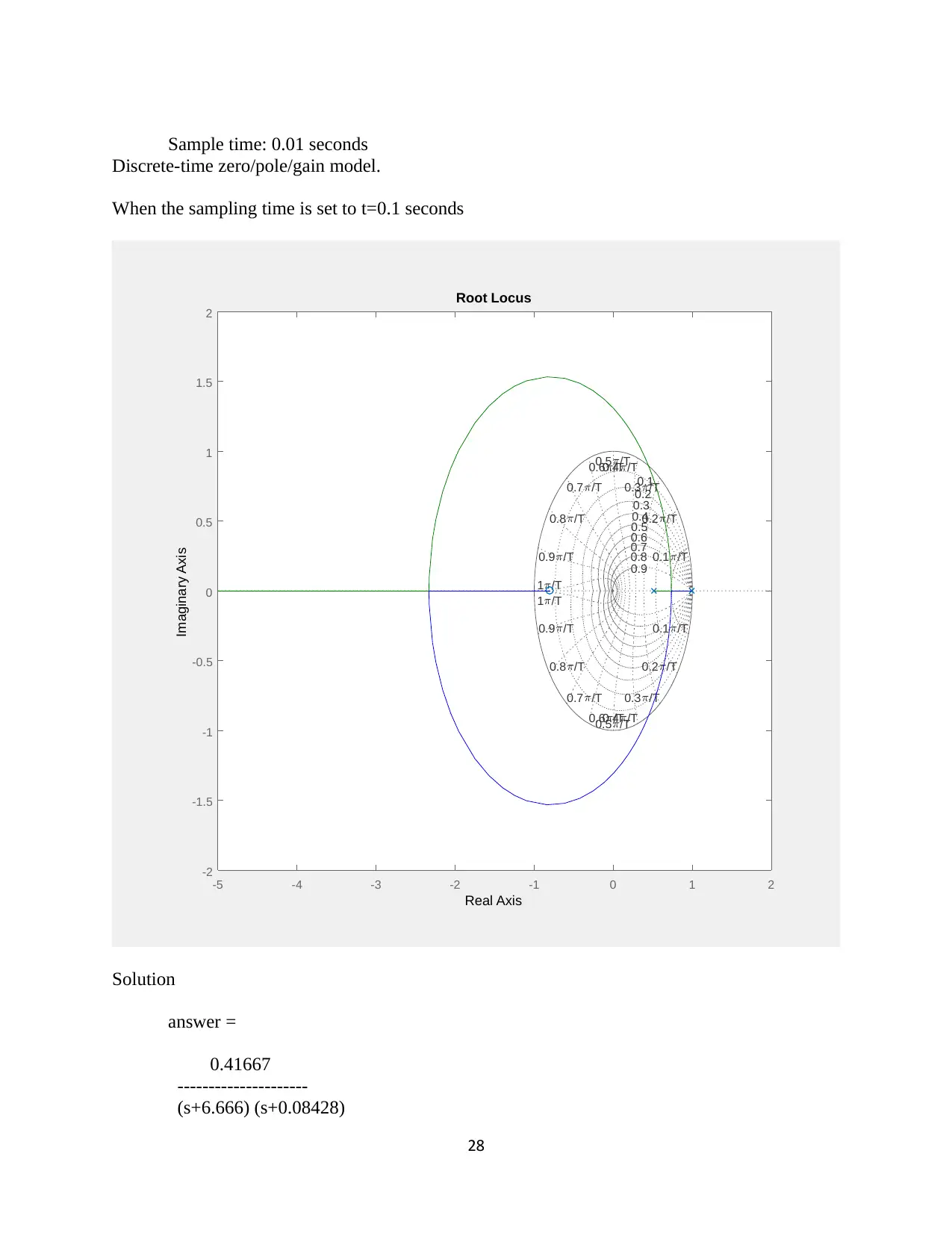
Sample time: 0.01 seconds
Discrete-time zero/pole/gain model.
When the sampling time is set to t=0.1 seconds
-5 -4 -3 -2 -1 0 1 2
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Root Locus
Real Axis
Imaginary Axis
Solution
answer =
0.41667
---------------------
(s+6.666) (s+0.08428)
28
Discrete-time zero/pole/gain model.
When the sampling time is set to t=0.1 seconds
-5 -4 -3 -2 -1 0 1 2
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Root Locus
Real Axis
Imaginary Axis
Solution
answer =
0.41667
---------------------
(s+6.666) (s+0.08428)
28

Continuous-time zero/pole/gain model.
ans =
0.0016833 (z+0.7991)
---------------------
(z-0.9916) (z-0.5135)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
When the sampling time is set to t=1 sec
29
ans =
0.0016833 (z+0.7991)
---------------------
(z-0.9916) (z-0.5135)
Sample time: 0.1 seconds
Discrete-time zero/pole/gain model.
When the sampling time is set to t=1 sec
29
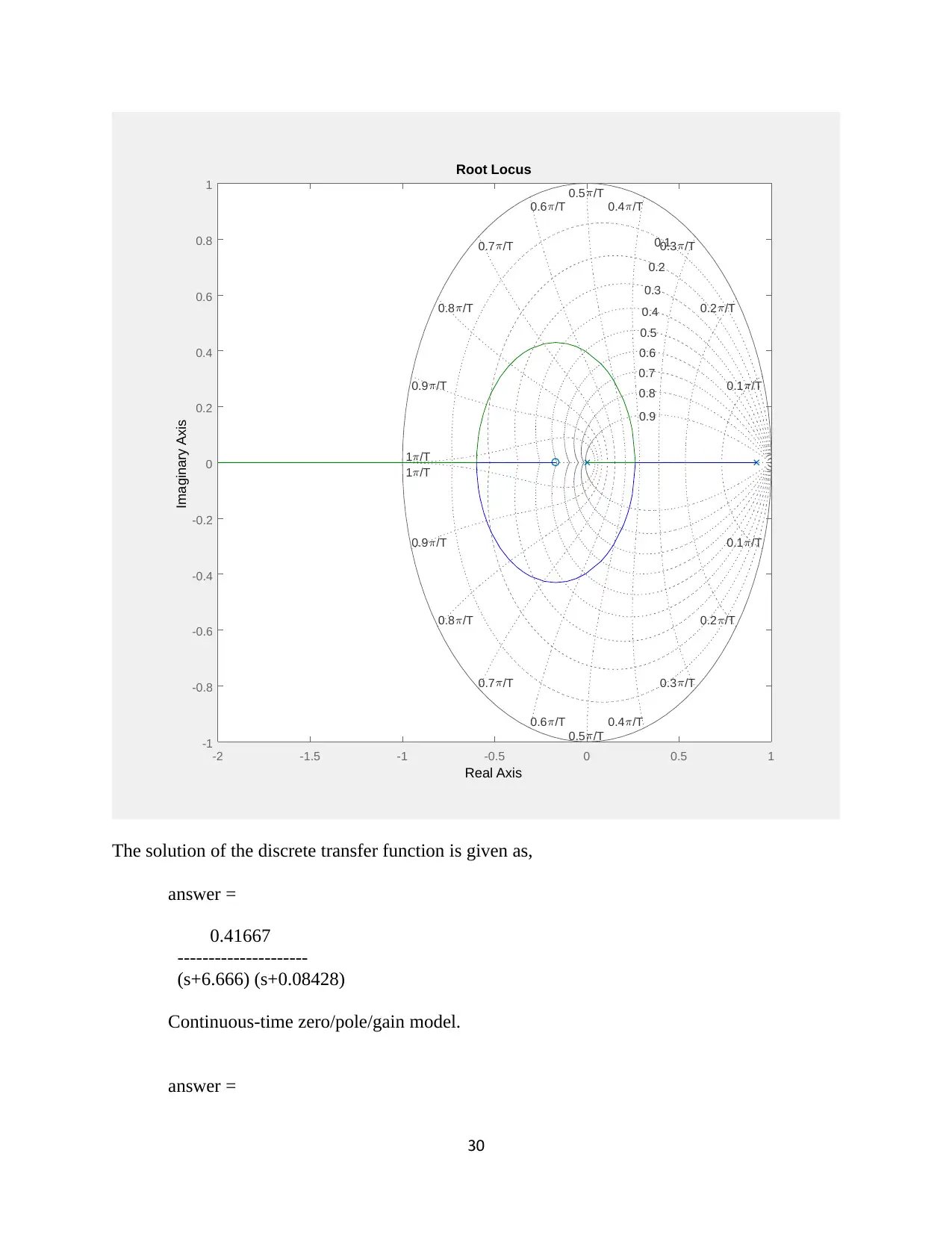
-2 -1.5 -1 -0.5 0 0.5 1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Root Locus
Real Axis
Imaginary Axis
The solution of the discrete transfer function is given as,
answer =
0.41667
---------------------
(s+6.666) (s+0.08428)
Continuous-time zero/pole/gain model.
answer =
30
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.7 /T
0.8 /T
0.9 /T
1 /T
0.1 /T
0.2 /T
0.3 /T
0.4 /T
0.5 /T
0.6 /T
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Root Locus
Real Axis
Imaginary Axis
The solution of the discrete transfer function is given as,
answer =
0.41667
---------------------
(s+6.666) (s+0.08428)
Continuous-time zero/pole/gain model.
answer =
30
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

0.051229 (z+0.1687)
-----------------------
(z-0.9192) (z-0.001274)
Sample time: 1 seconds
Discrete-time zero/pole/gain model.
Discussion
(iii) PID control in discrete conditions
Signals in real-life applications are set up in continuous time while for easier analysis
they need to be converted to digital mode. The discrete time mode occurs when the amplitude
between two consecutive time instants are not defined. The sampled data signal is obtained by
sampling the continuous time signals about a given period. These systems are used to attain the
optimal performance. They are obtained in the form of the maximum productivity; they provide
maximum profit at minimal manufacturing costs or minimal energy use. The design of the digital
controllers is carried out in the z-domain. The discrete time signals have amplitudes between two
consecutive time instants which is not defined but only on the particular time instance. The
sampled data signal is a discrete time signal resulting from sampling a continuous time signal.
Signals carry energy from one position to another. Linear systems and non-linear systems
are used to find out on the energy carried. Signals are patterns that form and the signals carry
certain information. The continuous time signals are the world’s most common signals are the
scale used is infinitesimal. Some of the parameter measured are the velocity of a mobile device
as well as the voltage of the electrical circuits. The discrete time signals are sampled continuous
time signals. Signals are considered periodic in that they tend to repeat themselves. The even and
odd signals are described as those whose negative sign means differently. The pulse signals are
31
-----------------------
(z-0.9192) (z-0.001274)
Sample time: 1 seconds
Discrete-time zero/pole/gain model.
Discussion
(iii) PID control in discrete conditions
Signals in real-life applications are set up in continuous time while for easier analysis
they need to be converted to digital mode. The discrete time mode occurs when the amplitude
between two consecutive time instants are not defined. The sampled data signal is obtained by
sampling the continuous time signals about a given period. These systems are used to attain the
optimal performance. They are obtained in the form of the maximum productivity; they provide
maximum profit at minimal manufacturing costs or minimal energy use. The design of the digital
controllers is carried out in the z-domain. The discrete time signals have amplitudes between two
consecutive time instants which is not defined but only on the particular time instance. The
sampled data signal is a discrete time signal resulting from sampling a continuous time signal.
Signals carry energy from one position to another. Linear systems and non-linear systems
are used to find out on the energy carried. Signals are patterns that form and the signals carry
certain information. The continuous time signals are the world’s most common signals are the
scale used is infinitesimal. Some of the parameter measured are the velocity of a mobile device
as well as the voltage of the electrical circuits. The discrete time signals are sampled continuous
time signals. Signals are considered periodic in that they tend to repeat themselves. The even and
odd signals are described as those whose negative sign means differently. The pulse signals are
31

those that are nearly completely zero and closely related to the short spike. A step signal, as the
one used in the simulation, is zero to a certain time and then tends to be constant, thereafter.
These attributes describe a list of useful signals which are input into systems and they produce
output signals. The continuous time systems represent how continuous signals are transformed
via differential equations. The discrete time systems represent how discrete signals are
transformed via difference equations.
The digital signal is obtained by two processes of sampling and quantizing. The digital
controls are used for achieving optimal performance in the form of maximum productivity,
maximum profit, minimum cost, and the use of minimum energy in production activities. The
advantages of the digital controls are that it has reduced cost as there is the bulk manufacturing
of the control systems, they are flexible in response to design changes, noise immunity, and they
are more useful in the modern control systems. Some analog control systems exhibit good
performances as compared to the digital control systems. Digital control systems tend to
introduce a delay in the loop. The loop contains both analog and digital signals to provide a
means for conversion from one form to another to be used by each sub-system. The systems are
designed in the Z-domain. Hence, they must be converted from the S-domain to the Z-domain
for discretization of the control systems (Dougherty & Cooper, 2003).
(iv) Discussion on the performance of PID control
Non-linear differential equations formulated in the magnetic field-fixed d, q coordinate system
describe the permanent magnet SM for the system development. The discrete time two-phase
oscillator produces the transformation matrix elements needed for the transformation blocks. A
high gain proportional control law with voltage saturation limits was used for simulation. The
bang-bang control law operating in the sliding mode is the switching strategy for the two-phase
32
one used in the simulation, is zero to a certain time and then tends to be constant, thereafter.
These attributes describe a list of useful signals which are input into systems and they produce
output signals. The continuous time systems represent how continuous signals are transformed
via differential equations. The discrete time systems represent how discrete signals are
transformed via difference equations.
The digital signal is obtained by two processes of sampling and quantizing. The digital
controls are used for achieving optimal performance in the form of maximum productivity,
maximum profit, minimum cost, and the use of minimum energy in production activities. The
advantages of the digital controls are that it has reduced cost as there is the bulk manufacturing
of the control systems, they are flexible in response to design changes, noise immunity, and they
are more useful in the modern control systems. Some analog control systems exhibit good
performances as compared to the digital control systems. Digital control systems tend to
introduce a delay in the loop. The loop contains both analog and digital signals to provide a
means for conversion from one form to another to be used by each sub-system. The systems are
designed in the Z-domain. Hence, they must be converted from the S-domain to the Z-domain
for discretization of the control systems (Dougherty & Cooper, 2003).
(iv) Discussion on the performance of PID control
Non-linear differential equations formulated in the magnetic field-fixed d, q coordinate system
describe the permanent magnet SM for the system development. The discrete time two-phase
oscillator produces the transformation matrix elements needed for the transformation blocks. A
high gain proportional control law with voltage saturation limits was used for simulation. The
bang-bang control law operating in the sliding mode is the switching strategy for the two-phase
32

version and is satisfactorily determined. Electric drive with synchronous motor consists of a
synchronous machine with nominal parameters (Dorf , n.d.).
(v) Simulation analysis conclusions
The PID controller implements a unity feedback loop. In some cases, it uses the varied feedback
depending on whether a sensor has been used to read the actual output and sends it to the
summer to check for errors. The continuous time signals are the world’s most common signals
are the scale used is infinitesimal. Some of the parameter measured is the velocity of a mobile
device as well as the voltage of the electrical circuits. The controller tends to generate an offset
value. These controllers increase the maximum overshoot of the system. The yielded signal tends
to have the offset minimized by an integral part when the integral element is added to the
proportional element. The past section and the recent trajectory of the controller error have no
impact on the proportional term as it is. The proportional corrects instances of error, the correct
integral accumulation of error, and the derivative corrects the present error in respect to the error
in the previous check. For many cases, we cannot obtain the same desired results in terms of
theoretical and practical cases. For that project, we have to make theoretical power calculations
for DC motors to obtain the desired DC motor speed. However, in practice, we could not obtain
the same results as it is calculated theoretically. For that purpose, we have to use controllers to
minimize the error between actual and theoretical results
33
synchronous machine with nominal parameters (Dorf , n.d.).
(v) Simulation analysis conclusions
The PID controller implements a unity feedback loop. In some cases, it uses the varied feedback
depending on whether a sensor has been used to read the actual output and sends it to the
summer to check for errors. The continuous time signals are the world’s most common signals
are the scale used is infinitesimal. Some of the parameter measured is the velocity of a mobile
device as well as the voltage of the electrical circuits. The controller tends to generate an offset
value. These controllers increase the maximum overshoot of the system. The yielded signal tends
to have the offset minimized by an integral part when the integral element is added to the
proportional element. The past section and the recent trajectory of the controller error have no
impact on the proportional term as it is. The proportional corrects instances of error, the correct
integral accumulation of error, and the derivative corrects the present error in respect to the error
in the previous check. For many cases, we cannot obtain the same desired results in terms of
theoretical and practical cases. For that project, we have to make theoretical power calculations
for DC motors to obtain the desired DC motor speed. However, in practice, we could not obtain
the same results as it is calculated theoretically. For that purpose, we have to use controllers to
minimize the error between actual and theoretical results
33
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

REFERENCES
“A General Approach to Control a Positive Buck Boost Converter to Achieve Robustness against
Input
Voltage Fluctuations and Load Changes,” IEEE Trans. Power Electronics, vol. 18, pp.
438-446, Jan 2003
Arbogast, J. & Dougherty, D., 2003. A multiple model adaptive control strategy for DMC.
[Online]
Available at: http://ieeexplore.ieee.org/document/1243451/
Chien-Ming Lee et. al, “LabVIEW Implementaton of an Auto-Tuning PID Regulator via Grey-
predictor,”
in Proc. IEEE-CISC, 2006, pp. 1-5
Dougherty, D. & Cooper, D., 2003. A practical multiple model adaptive strategy for single loop
MPC. [Online]
Available at: https://www.sciencedirect.com/science/article/pii/S0967066102001065?via
%3Dihub
Gu, D.-W., Petkov, H. P. & Konstantinov, M. M., 2013. Robust Control Design with Matlab (R).
2nd Edition ed. London: Springer Nature.
H Matsuo, F Kurokawa, H Etou, Y Ishizuka and C Chen, “Design oriented analysis of the
digitally controlled DC-DC converter,” in Proc. IEEE-PSEC, 2000, pp. 401-407.
L. Peng, X. Kang and J. Chen, “A novel PWM technique in digital control and its application to
an improved DC/DC converter,” in Proc. IEEE-PSEC, 2001, pp. 254-259.
34
“A General Approach to Control a Positive Buck Boost Converter to Achieve Robustness against
Input
Voltage Fluctuations and Load Changes,” IEEE Trans. Power Electronics, vol. 18, pp.
438-446, Jan 2003
Arbogast, J. & Dougherty, D., 2003. A multiple model adaptive control strategy for DMC.
[Online]
Available at: http://ieeexplore.ieee.org/document/1243451/
Chien-Ming Lee et. al, “LabVIEW Implementaton of an Auto-Tuning PID Regulator via Grey-
predictor,”
in Proc. IEEE-CISC, 2006, pp. 1-5
Dougherty, D. & Cooper, D., 2003. A practical multiple model adaptive strategy for single loop
MPC. [Online]
Available at: https://www.sciencedirect.com/science/article/pii/S0967066102001065?via
%3Dihub
Gu, D.-W., Petkov, H. P. & Konstantinov, M. M., 2013. Robust Control Design with Matlab (R).
2nd Edition ed. London: Springer Nature.
H Matsuo, F Kurokawa, H Etou, Y Ishizuka and C Chen, “Design oriented analysis of the
digitally controlled DC-DC converter,” in Proc. IEEE-PSEC, 2000, pp. 401-407.
L. Peng, X. Kang and J. Chen, “A novel PWM technique in digital control and its application to
an improved DC/DC converter,” in Proc. IEEE-PSEC, 2001, pp. 254-259.
34
APPENDIX
J=0.12; % Moment of inertia of the motor
b=0.01; % viscous fricion coefficient of the motor
Ke=0.015; % Back electromotive force
Kt=0.015; % Torque constant
R=2; % Resistance
L=0.3; % Inductance
K=Kt;
n1=3.3164e-06;
n2=n1*0.9949;
d1=1;
d2=-1.9848;
d3=0.9848264;
s=tf('s');
DC_motor=Kt/((J*s+b)*(L*s+R)+Kt*Ke);
disp(DC_motor)
%% displaying the state space
A=[-b/J K/J
-K/J -R/J];
B=[0
1/L];
C=[1 0];
D=0;
motor_ss=ss(A,B,C,D)
%% drawing the open loop root locus of the DC motor System
rlocus(DC_motor)
p2=pole(DC_motor)
grid on
%% PART C
wp=DC_motor; % system plant function
kp=input('Enter the Proportional constant (Kp)')
ki=input('Enter the Integral constantv (Ki)')
kd=input('Enter the Derivative constant(Kd)')
s=tf('s')
Wc=kp*(1+(1/(ki*s))+kd*s) %Ziegler Nichols PID tuning Method
%for a closed loop implementation
sys_2=feedback(series(wp,Wc),1) %unity feedback
rlocus(sys_2)
grid on
p1=pole(sys_2)
%% Discretization the system
zpk(DC_motor)
Ts=1;
DP_motor=c2d(DC_motor, Ts,'zoh');
zpk(DP_motor)
rlocus(DP_motor)
grid on
p2=pole(DP_motor);
35
J=0.12; % Moment of inertia of the motor
b=0.01; % viscous fricion coefficient of the motor
Ke=0.015; % Back electromotive force
Kt=0.015; % Torque constant
R=2; % Resistance
L=0.3; % Inductance
K=Kt;
n1=3.3164e-06;
n2=n1*0.9949;
d1=1;
d2=-1.9848;
d3=0.9848264;
s=tf('s');
DC_motor=Kt/((J*s+b)*(L*s+R)+Kt*Ke);
disp(DC_motor)
%% displaying the state space
A=[-b/J K/J
-K/J -R/J];
B=[0
1/L];
C=[1 0];
D=0;
motor_ss=ss(A,B,C,D)
%% drawing the open loop root locus of the DC motor System
rlocus(DC_motor)
p2=pole(DC_motor)
grid on
%% PART C
wp=DC_motor; % system plant function
kp=input('Enter the Proportional constant (Kp)')
ki=input('Enter the Integral constantv (Ki)')
kd=input('Enter the Derivative constant(Kd)')
s=tf('s')
Wc=kp*(1+(1/(ki*s))+kd*s) %Ziegler Nichols PID tuning Method
%for a closed loop implementation
sys_2=feedback(series(wp,Wc),1) %unity feedback
rlocus(sys_2)
grid on
p1=pole(sys_2)
%% Discretization the system
zpk(DC_motor)
Ts=1;
DP_motor=c2d(DC_motor, Ts,'zoh');
zpk(DP_motor)
rlocus(DP_motor)
grid on
p2=pole(DP_motor);
35
1 out of 36
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.




