Control & Instrumentation PDF

Control & Instrumentation
Lab Assignment
Student Name
Student ID Number
Instructor (professor)
Institutional affiliation
Location(state, country)
Date of submission

TABLE OF CONTENTS
INTRODUCTION...........................................................................................................................1
AIMS OF THE EXPERIMENT......................................................................................................3
ROTARY INVERTED PENDULUM SYSTEM MODEL.............................................................3
ROTARY INVERTED PENDULUM SIMULINK MODEL.........................................................7
CONTROLLER DESIGN...............................................................................................................8
DISCUSSION..................................................................................................................................8
CONCLUSION & FUTURE WORKS...........................................................................................8
REFERENCES................................................................................................................................9
LIST OF FIGURES
Figure 1 ROTPEN rotary inverted pendulum on LABVIEW [source: Quanser].........................................3
Figure 2 Free body diagram of the rotary inverted pendulum......................................................................4
Figure 3ROTPEN Matlab Simulink Model-Overview................................................................................9
Figure 4 Step response ROTPEN Matlab Simulink Model Output............................................................12
Figure 5 Bode Diagram to show magnitude and phase of ROTPEN Pendulum........................................13
Figure 6 Open loop system Simulation Model Block................................................................................14
Figure 7 Root Locus for Transfer Function 1............................................................................................15
Figure 8 Root Locus for transfer function 2...............................................................................................16
Figure 9 Pole location for a closed loop system........................................................................................18
Figure 10 State feedback controller for a closed loop ROTPEN pendulum...............................................18
Figure 11 The ROTPEN controller for the Pendulum link........................................................................19
Figure 12 System Simulation Balance Control Response for the closed loop............................................20
Figure 13 Results form Simulation of the ROTPEN model.......................................................................21
Figure 14 ROTPEN Model........................................................................................................................22
Figure 15 State Feedback controller segment............................................................................................22
1 | P a g e

INTRODUCTION
The rotary inverted pendulum is a nonlinear system whose initial state is unstable hence
the need for control. There are different methods implemented in the control of the rotary
inverted pendulum. In the analysis, the velocity of the pendulum center of mass, is considered for
a system displaced in the angle, a, and in the x-direction [1]-[5]. The system has a motor that
moves the cart along a straight track with the pendulum attached to the cart using a pin joint. The
axis of rotation of the pendulum link is considered to be horizontal and it is perpendicular to the
cart’s direction of motion. The input of the system is the force that is applied to the cart through
the motor. The horizontal link is coupled such that it links directly or by connecting to a gearing
of the motor shaft and the rotary motion [6]. The QNET rotary inverted pendulum kit is
comprised of the dc motor, L-shaped arm, and pendulum, and two optical encoders, Elvis II
board. The motor that runs the pendulum is mounted on a metallic chamber. The pendulum is
suspended on a horizontal axis at the end of the arm. The pendulum and arm angle are measured
by two separate encoders [7]. The control variable is the input voltage to the pulse width
modulated amplifier that controls the motor.
Figure 1 ROTPEN rotary inverted pendulum on LABVIEW [source: Quanser]
2 | P a g e

The rotary inverted pendulum is applied in the industries especially where items need to
be lifted from one point to another. The same system is implemented in robots and in the large
cranes used in the construction industry [8]. In some mall, the system is used to design the
Segway used to by security guards to monitor the premises. The ROTPEN kit in the 2 DOF
freely moves in two rotary directions.
AIMS OF THE EXPERIMENT
(a) To linearize a non-linear rotary inverted pendulum systems using Euler-Lagrange
equations of motion.
(b) To define the linear state-space representation of the rotary inverted pendulum system
(c) To develop a state-feedback or full feedback control to balance the pendulum in the
upright position using a pole placement.
(d) To simulate the open-loop and the closed loop systems of the ROTPEN inverted
pendulum so that the specifications are met and evaluating the performance.
3 | P a g e

ROTARY INVERTED PENDULUM SYSTEM MODEL
The system is modeled mathematically focusing on the rotational direction of the rotary
inverted pendulum arm. It is assumed that the system starts in the state of equilibrium and the
initial conditions are assumed to be zero [9]. The pendulum is set to move very few degrees
away from the vertical direction in order to satisfy the linear model.
Figure 2 Free body diagram of the rotary inverted pendulum
The velocity components of the rotary inverted pendulum in the x-direction are obtained
as,
V penCOM =−Lcos α ( ˙α ) ^x−L sin α ( ˙α ) ^y
Considering the rotating arm,
V arm=r ˙θ
The x and y velocity components are expressed as,
vx=r ˙θ−L cos α ( ˙α )
v y=−Lsin α ( ˙α )
Obtaining the system dynamic equation based on the Euler-Lagrange Formulation,
4 | P a g e

V =P Epend =mgh=mgL cos α
T =K Ehub +K EV x
+ K EV y
+ K Epend
The moment of inertia for a rod is given based on the center of mass, such that,
Jcm=( 1
12 ) M R2
The half of the pendulum length is described as L such that,
R=2 L
Jcm=( 1
12 ) M (2 L)2= ( 1
3 )M L2
The kinetic energy equation can be written as,
T =( 1
2 ) Jeq ˙θ2+ ( 1
2 )m ( r ˙θ−Lcos α ( ˙α ) )2+ ( 1
2 )m (−L sin α ( ˙α ) )2 + (1
2 )Jcm ˙α2
Determining the KE function using the Lagrangian formulation, the equation results into,
L=T −V =( 1
2 )J eq ˙θ2 + ( 2
3 )m L2 ˙α2−mLr cos α ( ˙α ) ( ˙θ ) + (1
2 )m r2 ˙θ2−mgL cos α
The two equations are used to obtain the angular components,
δ
δt ( δL
δ ˙θ )− δL
δθ =T output−Beq ˙θ
δ
δt ( δL
δ ˙α )− δL
δα =0
Linearizing the equation at α=0,
5 | P a g e

( J eq+m r2 ) ¨θ−mLr ¨α=T output−Beq ˙θ
4
3 m L2 ¨α−mLr ¨θ−mgLα=0
The torque of the motor that powers the rotary action of the rotary inverted pendulum is given as,
T output= ηm ηg K t K g ( V m−K G K m ˙θ )
Rm
All the governing equations are combined to represent the complete system operation using the
state space representation below,
[ ˙θ
˙α
¨θ
¨α ]=
[0 0 1 0
0 0 0 1
0 bd
E
−cG
E 0
0 qd
E
−bG
E 0 ] [ θ
α
˙θ
˙α ]+
[ 0
0
C ηm ηg Kt K g
Rm E
b ηm ηg Kt Kg
Rm E ]V m
a=J eq+mr2, b=mLr, c= 4
3 m L2
, d=mgL, E=ac−b2
G= ηm ηg K t K g
2−Beq Rm
Rm
Using the Euler equation of the rotational motion of the pendulum at the pin point, we get the
equation,
JB ¨α=∑ M B → 1
12 m ( 2 L )2 ¨α= Ax Lcos ( α ) + A y L sin ( α )
→ 1
3 m L2 ¨α −Ax Lcos α + A y L sin ( α )
Jo ¨θ=∑ M 0 → J eq ¨θ=T1−Beq ˙θ− Ax r
6 | P a g e

1
3 m L2 ¨α= ( mr ¨θ+mL sin ( α ) ˙α 2−mL cos ( α ) ¨α L cos ( α ) )+ ( mg−mL cos ( α ) ˙α 2−mL sin ( α ) ¨α ) L sin α
→ 1
3 m L2 ¨α= (mLr cos ( α ) ¨θ+m L2 sin ( α ) cos ( α ) ˙α2−m L2 cos2 ( α ) ¨α )+ (mgLsin ( α )−m L2 sin ( α ) cos ( α ) ˙α2−m L2 sin2 ( α
→−mLr cos ( α ) ¨θ+ 4
3 m L2 ¨α−mgLsin ( α )=0
ROTARY INVERTED PENDULUM SIMULINK MODEL
The rotary inverted pendulum Simulink model is developed for a nonlinear system. The
system depends on a MATLAB script that highlights all the values of the system parameters
7 | P a g e

which the Simulink obtains from the workspace once it is run. The nonlinear equation of motion
is rearranged so as to obtain an acceleration form of the equation, with respect to the Newtonian
law of motion [10]. The system uses some parameters which are saved in a parameter file which
is accessed by the ROTPEN simulation model,
%% ROTPEN Parameters
Mp=0.027;
Lp=0.153;
r=0.0826;
Jp=0.00017;
Jeq=0.00018;
kt=0.0333;
km=0.0333;
Rm=8.7;
g=9.81;
B1=0.001;
B2=0.001;
The formulation of the rotary inverted pendulum model within the MATLAB Simulink
environment requires a previous familiarization with MATLAB and the Simulink software. The
model being used obtains its parameters from a script file. The following is an illustration of the
simulation model,
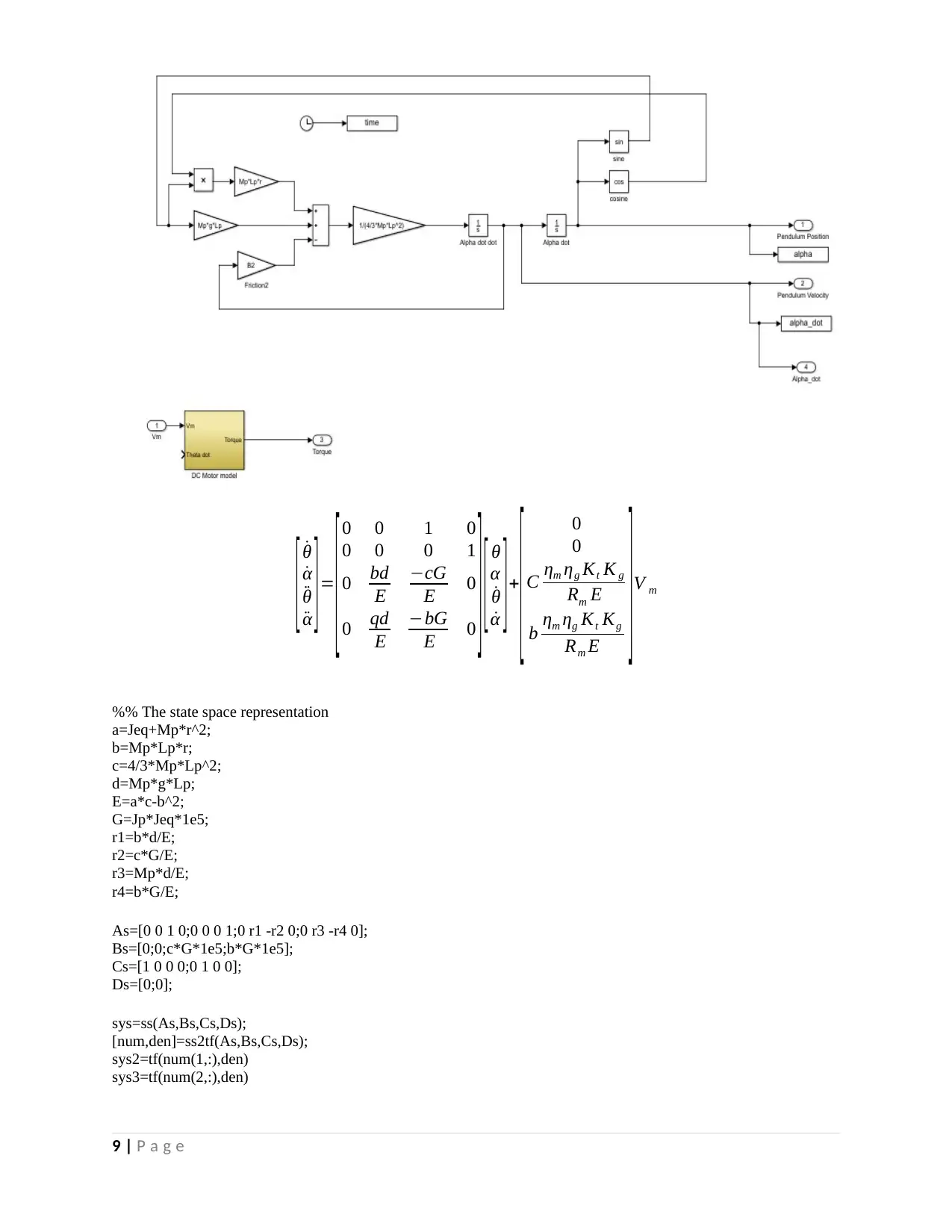
Figure 3ROTPEN Matlab Simulink Model-Overview
The ROTPEN system implements the Lagrange equation in the State-space representation form,
8 | P a g e

[ ˙θ
˙α
¨θ
¨α ]=
[0 0 1 0
0 0 0 1
0 bd
E
−cG
E 0
0 qd
E
−bG
E 0 ] [ θ
α
˙θ
˙α ]+
[ 0
0
C ηm ηg Kt K g
Rm E
b ηm ηg Kt Kg
Rm E ]V m
%% The state space representation
a=Jeq+Mp*r^2;
b=Mp*Lp*r;
c=4/3*Mp*Lp^2;
d=Mp*g*Lp;
E=a*c-b^2;
G=Jp*Jeq*1e5;
r1=b*d/E;
r2=c*G/E;
r3=Mp*d/E;
r4=b*G/E;
As=[0 0 1 0;0 0 0 1;0 r1 -r2 0;0 r3 -r4 0];
Bs=[0;0;c*G*1e5;b*G*1e5];
Cs=[1 0 0 0;0 1 0 0];
Ds=[0;0];
sys=ss(As,Bs,Cs,Ds);
[num,den]=ss2tf(As,Bs,Cs,Ds);
sys2=tf(num(1,:),den)
sys3=tf(num(2,:),den)
9 | P a g e

figure(1)
rlocus(sys2)
grid on
figure(2)
rlocus(sys3)
grid on
figure(3)
subplot(2,1,1)
step(sys2)
grid on
subplot(2,1,2)
step(sys3)
grid on
figure(4)
subplot(2,1,1)
bode(sys2)
grid on
subplot(2,1,2)
bode(sys3)
grid on
Free response
Considering that f=0, the actual values are replaced in the equation,
10 | P a g e

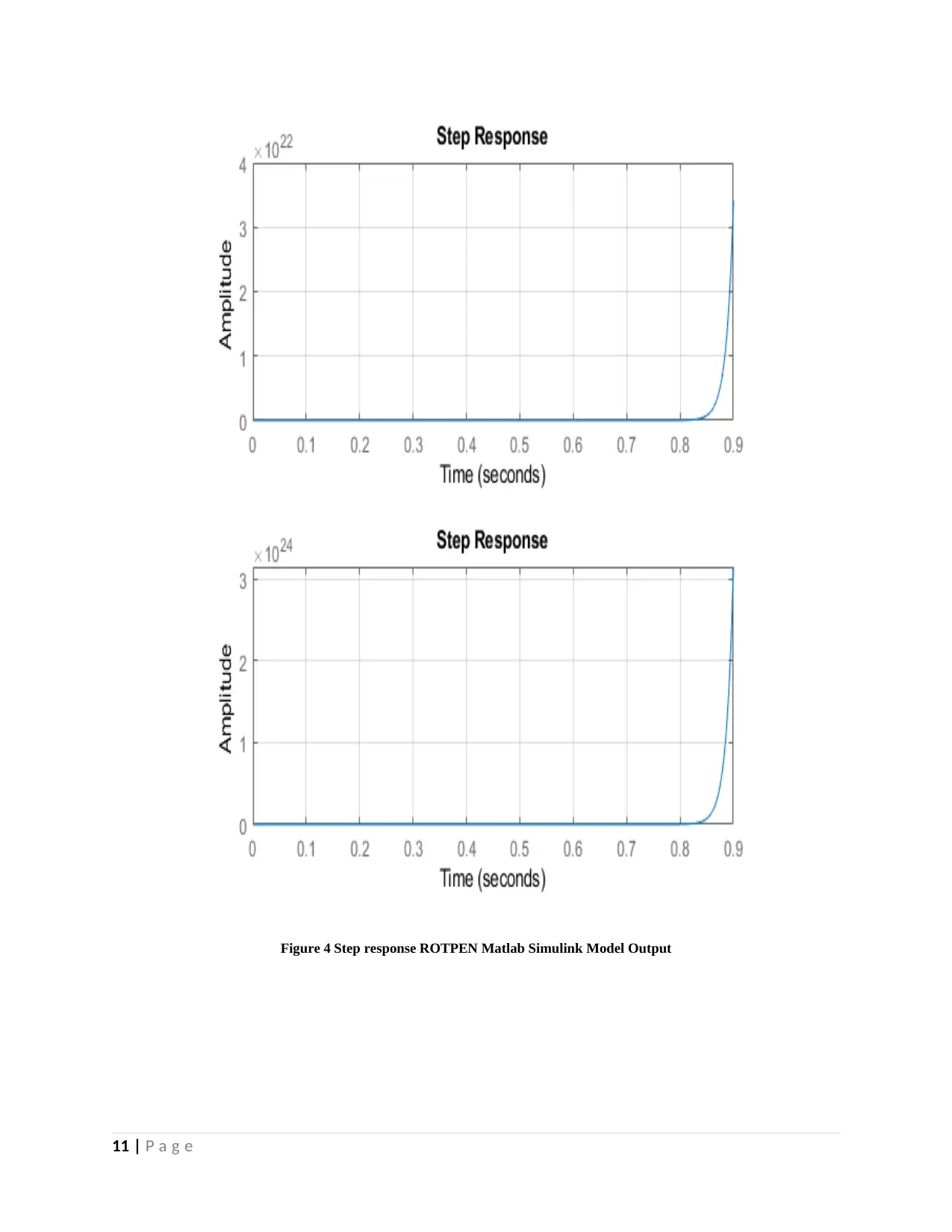
Figure 4 Step response ROTPEN Matlab Simulink Model Output
11 | P a g e

To determine the magnitude and phase plots
-100
-50
0
Magnitude (dB)
10-1 100 101 102 103
-180
-135
-90
Phase (deg)
Bode Diagram
Frequency (rad/s)
-140
-120
-100
Magnitude (dB)
10-1 100 101 102 103
-180
-135
-90
Phase (deg)
Bode Diagram
Frequency (rad/s)
Figure 5 Bode Diagram to show magnitude and phase of ROTPEN Pendulum
12 | P a g e

CONTROLLER DESIGN
(i) Open Loop System Simulation Results
An open loop system is comprised of an input, process, and output. The system
contains system simulation processes with NO feedback loop hence the output from
the system may not, necessarily, be bounded.
Figure 6 Open loop system Simulation Model Block
The stability response of the system is tested using the root locus for the two transfer
functions,
For transfer function 1:
13 | P a g e

Figure 7 Root Locus for Transfer Function 1
For transfer function 2:
14 | P a g e

Figure 8 Root Locus for transfer function 2
(ii) Linearization Process Around Pendulum Angle
Using the mathematical approach, the linear state space model is given as,
˙x= Ax+ Bu
y=Cx + Du
The rotary pendulum system state and output are given as,
xT= [ θ α ˙θ ˙α ]
yT = [ x1 x2 ]
( mp Lr
2+J r ) ¨θ−1
2 mp Lp Lr ¨α=τ−Br ˙θ
The initial conditions are set such that,
[ θ
α
˙θ
˙α ] =
[ 0
0
0
0 ]
15 | P a g e

f ( z ) =−1
2 mp Lp Lr cos ( α ) ¨θ+ ( J p + 1
4 mp Lp
2
) ¨α
¿− 1
4 mp Lp
2 cos ( α ) sin ( α ) ˙θ2− 1
2 mp Lp g sin ( α )
The solutions are derived from the derivatives of the function f(z),
f lin ( z ) =−1
2 mp Lp Lr ¨θ +(J p + 1
4 mp Lp
2
) ¨α − 1
2 mp Lp gα =−Bp ˙α
Using MATLAB to derive the linear system,
%% Linearising the model
[As1,Bs1,Cs1,Ds1]=linmod('ROTPEN_ModelNL.mdl',[0;0;0;0],0)
It is quite crucial to choose a good set of initial conditions when linearizing the model to avoid
spikes or instances where the system loses stability in the resulting linear model.
(iii) Design Of Full Feedback Controller Based On Linearized Model
The pole placement is guided by the equation below in state space form,
˙x= Ax+ B (−Kx )
¿( A−BK ) x
The characteristic equation is obtained to have the closed loop pole locations as,
16 | P a g e

Figure 9 Pole location for a closed loop system
To design a full feedback controller based on the linearized model,
Figure 10 State feedback controller for a closed loop ROTPEN pendulum
The controller is given as,
u= {K ( xd −x )|x2|< ε
0 otherwise
%% Full feedback controller for linearized model
K=Kt*Km;
eig(As-Bs*K)
% pole placement
poles=[-19.5615;-6.2370+2.0742i;-6.2370-2.0742i;-6.0937];
K= place(A,B,poles);
poles_calc = eig(A-B*K);
figure();
hold all;
plot(real(poles),imag(poles),'o')
17 | P a g e

plot(real(poles_calc),imag(poles_calc),'d');
title('Pole Placement: specified and resulting poles')
xlabel('Real (Hz)')
ylabel('Imaginary (Hz)')
legend('Specified poles','Calculated poles');
grid on;
The controller design is obtained from the following parameters such that,
[−36.49 41.8 82.3 0
0 −35.6 81.2 0
0 −32.14 408 82.1
0 0 −23.4 76.5 ]=transformation ¿
maxdefl❑=8.3
To determine the swing up control of the pendulum,
J p ¨α + 1
2 mp g Lp sin(α)= 1
2 mp Lp u cos α
The acceleration of the pendulum link base is given as,
τ =mr Lr u
Figure 11 The ROTPEN controller for the Pendulum link
(iv) Closed Loop System Simulation Results
18 | P a g e

Adding a controller and a feedback loop transforms an open loop system to a
closed loop system. The feedback loop seeks to check if the output obtained is equal
to the desired output. When it varies, an error is detected and corrected by the
controller. Implementing the full feedback controller in the ROTPEN_model, the
simulated closed loop balance control response is given as,
Figure 12 System Simulation Balance Control Response for the closed loop
Using the MATLAB plot command, the figure is given such that the response obtained
forms,
19 | P a g e

Figure 13 Results form Simulation of the ROTPEN model
DISCUSSION
The types of control schemes applied in the real world application for the control of
inverted pendulum include the PID controller for a two degree of freedom system as well as the
state feedback control scheme. In some advanced systems, the fuzzy logic controllers are used
especially where the inputs and the anticipated outputs are predefined. The fuzzy logic
controllers can be implemented alongside the PID to improve the control of the system and
anticipate uncertainties. A control sub-system regulates or commands one key function in the
system. Simulating the rotary inverted pendulum, gives the student a chance to test different
scenarios and observe the outputs on the scope feature of the Simulink model. The system
performance based on the energy and torque produced, demonstrates an instance of slight energy
loss which would cause a huge problem in a real application hence the need for a controller [11].
To determine the total energy in the system, the following section of the ROTPEN model is
developed,
20 | P a g e

Figure 14 ROTPEN Model
Figure 15 State Feedback controller segment
DISCUSSION
Comparing with the real life system from the experiment, the movement of the rotary inverted
pendulum is as illustrated on the system response as shown below,
21 | P a g e

CONCLUSION & FUTURE WORKS
In a nutshell, it is observed that the motion of the pendulum is on the x-direction where it
moves back and forth. The acceleration is increased to increase the energy exerted on the
pendulum such that the pendulum moves up and down. Increasing the acceleration to the
optimum point gives the pendulum a vertical position and the angle of the inverted pendulum
tends to be orthogonal to the cart. The rotary inverted pendulum forms two transfer functions
which perform differently but they share a common characteristic equation. The difference is felt
at the numerator where the zeros have different locations.
22 | P a g e

REFERENCES
[1]. Masanori Yukitomo, Takashi Shigemasa, Yasushi Baba, Fumia Kojima, “A Two
Degrees of Freedom PID Control System, its Features and Applications”, 2004 5th Asian
Control Conference.
[2]. Purtojo, R. Akmeliawati and Wahyudi, “Two-parameter Compensator Design for Point-
to-point (PTP) Positioning System Using Algebraic Method”, The Second International
Conference on Control, Instrumentation and Mechatronic Engineering (CIM09),
Malacca, Malaysia, June 2-3, 2009.
[3]. Mituhiko Araki and Hidefumi Taguchi, “Two-Degree-of-Freedom PID Controllers”,
International Journal of Control, Automation, and Systems Vol. 1, No. 4, December
2003.
[4]. M Gopal, Digital Control and State Variable methods Conventional and Neural-Fuzzy
Control System, 2nd edition, International Edition 2004, Mc Graw Hill, ISBN 0-07-
048302-7, Printed in Singapore.
[5]. Md. Akhtaruzzaman, Dr. Rini Akmeliawati and Teh Wai Yee. “Modeling and Control of
a Multi degree of Freedom Flexible Joint Manipulator”. 2009 Second International
Conference on Computer and Electrical Engineering (ICCEE `09), DUBAI, UAE, 28 –
30 Dec. 2009. p. 249 – 254.
[6]. Md. Akhtaruzzaman and A. A. Shafie”Control of a Rotary Inverted Pendulum Using
Various Methods, Comparative Assessment and Result Analysis” International
Conference on Mechatronics and AutomationAugust 4-7, 2010, Xi'an, China
[7]. Swing-Up and Stabilization of Rotary Inverted Pendulum, Mertl, Jaroslav Sobota, Milo·s
Schlegel, Pavel Balda,
[8]. Purtojo, R. Akmeliawati and Wahyudi, “Two-parameter Compensator Design for Point-
to-point (PTP) Positioning System Using Algebraic Method”, The Second International
Conference on Control, Instrumentation and Mechatronic Engineering (CIM09),
Malacca, Malaysia, June 2-3, 2009.
[9]. Mituhiko Araki and Hidefumi Taguchi, “Two-Degree-ofFreedom PID Controllers”,
International Journal of Control, Automation, and Systems Vol. 1, No. 4, December
2003.
[10]. M Gopal, Digital Control and State Variable methods Conventional and Neural-Fuzzy
Control System, 2nd edition, International Edition 2004, Mc Graw Hill, ISBN 0-07-
048302-7, Printed in Singapore.
23 | P a g e

[11]. Md. Akhtaruzzaman, Dr. Rini Akmeliawati and Teh Wai Yee. “Modeling and Control
of a Multi degree of Freedom Flexible Joint Manipulator”,2009 Second International
Conference on Computer and Electrical Engineering (ICCEE `09), DUBAI, UAE, 28 –
30 Dec. 2009. p. 249 – 254.
24 | P a g e