Source codes for Maximum Flow Algorithm

The java program above implements an algorithm called Fold-Fulkerson with a LinkedList data structure. Since it is an implementation of Edmonds-Karp algorithm, the worst time complexity is O(VE 2) and an adjacency matrix representation of O(V 2), hence the above implementation has O(EV 3) Time complexity.

Corrected Source codes for part 1.
1.)
import java.lang.*;
import java.io.*;
import java.util.LinkedList;
public class MaximumFlow
{
static final int V = 6;//allocate Number of vertices for the graph
//Boolean method for bfs to return true if we have a path source "s"
//to sink "t" in residual graph while storing paths in parent array
boolean bfs(int residualGraph[][], int source, int sink, int parent[])
{
//lets create a visit array and mark it as false(not visited//) by default
boolean visit[] = new boolean[V];
for(int i=0; i<V; ++i)
visit[i]=false;
//enqueue a source vertex "s" to the LinkedList and mark as visited.
LinkedList<Integer> queue = new LinkedList<Integer>();
queue.add(source);
visit[source] = true;
parent[source]=-1;
while (queue.size()!=0)
{
int u = queue.poll();
for (int v=0; v<V; v++)
{

if (visit[v]==false && residualGraph[u][v] > 0)
{
queue.add(v);
parent[v] = u;
visit[v] = true;
}
}
}
// If we reached sink in BFS starting from source, then
// return true, else false
return (visit[sink] == true);
}
int fordFulkerson(int graph[][], int source, int sink)
{
int u, v;
//if in our residual graph residualGraph[i][j] indicates
//residual capacity of edge from i to j (if an edge exist and if
// it is 0,then we don't have)
int residualGraph[][] = new int[V][V];
for(u = 0; u < V; u++)
for(v = 0; v < V; v++)
residualGraph[u][v] = graph[u][v];
int parent[] = new int[V];
int maxFlow = 0;//Initially we don't have a flow
//Lets Augment our flow as long as we have a path from

//source to sink
while(bfs(residualGraph, source, sink, parent))
{
//lets find maximum flow through the path found
int pathFlow = Integer.MAX_VALUE;
for(v = sink; v != source; v = parent[v])
{
u = parent[v];
pathFlow = Math.min(pathFlow, residualGraph[u][v]);
}
//now update residual capacities of the edges
//and reverse the edges along the path
for(v = sink; v != source; v = parent[v])
{
u = parent[v];
residualGraph[u][v] -= pathFlow;
residualGraph[v][u] += pathFlow;
}
maxFlow += pathFlow;
}
return maxFlow;//return maximum flow
}
//Driver program
public static void main(String[] args) throws Exception
{
int graph [][] = new int[][]{{0, 16, 13, 0, 0, 0},
{0, 0, 10, 12, 0, 0},
{0, 4, 0, 0, 14, 0},
{0, 0, 9, 0, 0, 20},

{0, 0, 0, 7, 0, 4},
{0, 0, 0, 0, 0, 0}
};
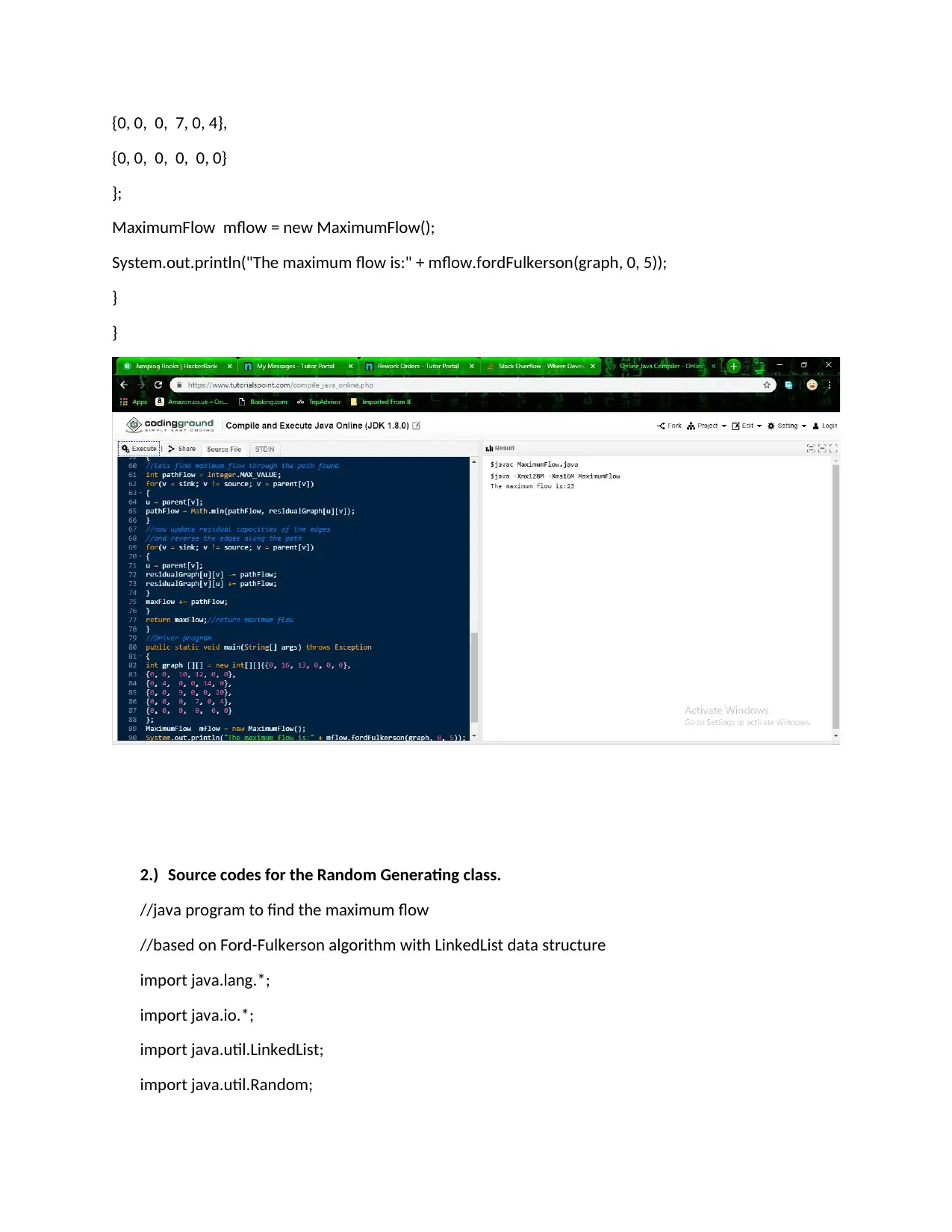
MaximumFlow mflow = new MaximumFlow();
System.out.println("The maximum flow is:" + mflow.fordFulkerson(graph, 0, 5));
}
}
2.) Source codes for the Random Generating class.
//java program to find the maximum flow
//based on Ford-Fulkerson algorithm with LinkedList data structure
import java.lang.*;
import java.io.*;
import java.util.LinkedList;
import java.util.Random;

public class MaximumFlow
{
static int V = 6;//allocate Number of vertices for the graph
//Boolean method for bfs to return true if we have a path source "s"
//to sink "t" in residual graph while storing paths in parent array
boolean bfs(int residualGraph[][], int source, int sink, int parent[])
{
//lets create a visit array and mark it as false(not visited//) by default
boolean visit[] = new boolean[V];
for(int i=0; i<V; ++i)
visit[i]=false;
//enqueue a source vertex "s" to the LinkedList and mark as visited.
LinkedList<Integer> queue = new LinkedList<Integer>();
queue.add(source);
visit[source] = true;
parent[source]=-1;
while (queue.size()!=0)
{
int u = queue.poll();
for (int v=0; v<V; v++)
{
if (visit[v]==false && residualGraph[u][v] > 0)
{
queue.add(v);
parent[v] = u;
visit[v] = true;

}
}
}
// If we reached sink in BFS starting from source, then
// return true, else false
return (visit[sink] == true);
} int fordFulkerson(int graph[][], int source, int sink)
{
int u, v;
//if in our residual graph residualGraph[i][j] indicates
//residual capacity of edge from i to j (if an edge exist and if
// it is 0,then we don't have)
int residualGraph[][] = new int[V][V];
for(u = 0; u < V; u++)
for(v = 0; v < V; v++)
residualGraph[u][v] = graph[u][v];
int parent[] = new int[V];
int maxFlow = 0;//Initially we don't have a flow
//Lets Augment our flow as long as we have a path from
//source to sink
while(bfs(residualGraph, source, sink, parent))
{
//lets find maximum flow through the path found
int pathFlow = Integer.MAX_VALUE;
for(v = sink; v != source; v = parent[v])
{

u = parent[v];
pathFlow = Math.min(pathFlow, residualGraph[u][v]);
}
//now update residual capacities of the edges
//and reverse the edges along the path
for(v = sink; v != source; v = parent[v])
{
u = parent[v];
residualGraph[u][v] -= pathFlow;
residualGraph[v][u] += pathFlow;
}
maxFlow += pathFlow;
}
return maxFlow;//return maximum flow
}
//Program to generate random integers within the given range
static int generateRandomIntRange(int min, int max)
{
Random r = new Random();
return r.nextInt((max - min)+ 1) + min;
}
//Driver program
public static void main(String[] args) throws Exception
{
MaximumFlow mflow = new MaximumFlow();
int V = mflow.generateRandomIntRange(5,20);
mflow.V = V;
int nodes[] = new int[12];
int Graph[][] = new int[V][V];//at most is twelve inclusive of source and //sink

//to generate the nodes based on our random method
for(int i = 0;i < 12;i++)
{
nodes[i] = mflow.generateRandomIntRange(0, 12);
}
for(int u =0;u < Graph.length;u++)
{
for(int v = 0;v < Graph[u].length; v++)
{
Graph[u][v] = u;
}
}
System.out.println("The maximum flow is:" + mflow.fordFulkerson(Graph, 0, V-1));//prints
maximumFlow else zero.
}
}

3.) Performance analysis.
The java program above implements an algorithm called Fold-Fulkerson with a LinkedList data structure.
Since it is an implementation of Edmonds-Karp algorithm, the worst time complexity is O(VE2) and an
adjacency matrix representation of O(V2), hence the above implementation has O(EV3) Time complexity.