THE COURSEWORK RESIT
VerifiedAdded on 2022/09/05
|9
|826
|20
AI Summary
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

Running head: COURSEWORK RESIT
COURSEWORK RESIT
Name of the Student
Name of the University
Author Note
COURSEWORK RESIT
Name of the Student
Name of the University
Author Note
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1COURSEWORK RESIT
1.
Given statement: If n is an odd number, then 4n-1 is prime.
Given, n is odd so let, n = 2m + 1 (where m = any positive whole number)
Thus, 4n-1 = 4*(2m+1) – 1 = 8m + 3.
Now, if 8m +3 is prime then (8m+3) mod m ≠ 0 for all m.
By, inspection it is found that when m = 3 then (8m+3) mod 3 = 27 mod 3 = 0. Hence,
(8m+3) is not prime.
Hence, the statement “If n is an odd number, then 4n-1 is prime” is false.
Converse statement: if 4n-1 is prime then n is an odd number.
By inspection, when n = 2 then 4n – 1 = 7 which is a prime number. Thus n can also be even
when 4n-1 is prime.
Thus the statement “if 4n-1 is prime then n is an odd number” is false.
2.
Given, there are 12 natural numbers in set A. Thus by using the pigeonhole principle when
divided by 11 then at least two of the 12 numbers must produce same remainder as the
numbers are different.
Let, the two numbers are ai and a j.
Hence, ai = 11k + r
a j = 11m + r
Where, k, m and r any integer.
1.
Given statement: If n is an odd number, then 4n-1 is prime.
Given, n is odd so let, n = 2m + 1 (where m = any positive whole number)
Thus, 4n-1 = 4*(2m+1) – 1 = 8m + 3.
Now, if 8m +3 is prime then (8m+3) mod m ≠ 0 for all m.
By, inspection it is found that when m = 3 then (8m+3) mod 3 = 27 mod 3 = 0. Hence,
(8m+3) is not prime.
Hence, the statement “If n is an odd number, then 4n-1 is prime” is false.
Converse statement: if 4n-1 is prime then n is an odd number.
By inspection, when n = 2 then 4n – 1 = 7 which is a prime number. Thus n can also be even
when 4n-1 is prime.
Thus the statement “if 4n-1 is prime then n is an odd number” is false.
2.
Given, there are 12 natural numbers in set A. Thus by using the pigeonhole principle when
divided by 11 then at least two of the 12 numbers must produce same remainder as the
numbers are different.
Let, the two numbers are ai and a j.
Hence, ai = 11k + r
a j = 11m + r
Where, k, m and r any integer.

2COURSEWORK RESIT
Thus ai−a j=11 k +r −11m−r = 11(k-m)
Thus ai−a j is divisible by 11.
Hence, by using the pigeonhole principle it proved that A contains at least two number ai and
a j such that ai−a j is divisible by 11.
3.
Given equation 5x – 12 = 0 in Z13.
Hence, it is required to find an element x such that
(5x-12) mod 13 = 0
Since, 0 = (m*13) mod 13 hence, 5x -12 = 13m
Now, xϵ {0,1,2,3,4,5,6,7,8,9,10,11,12 }
Hence, 5x -12 ϵ {−12 ,−7 ,−2,3,8,13,18,23,28,33,38,43,48}
In the set there is only one number matching to the form 13m which is 13 that is for x = 1.
Hence, the solution of 5x – 12 = 0 in Z13 is x = 1.
Given, x^2 – x – 1 = 0 in Z11.
Thus it required to find an element x such that
(x^2 – x – 1) mod 11 = 0
Since, 0 = (m*11) mod 11 hence, (x^2 – x – 1) = 11m
Now, xϵ {0,1,2,3,4,5,6,7,8,9,10}
Hence, (x^2 – x – 1) ϵ {−1 ,−1,1,5,11,19,29,41,55,71,89 }
Thus ai−a j=11 k +r −11m−r = 11(k-m)
Thus ai−a j is divisible by 11.
Hence, by using the pigeonhole principle it proved that A contains at least two number ai and
a j such that ai−a j is divisible by 11.
3.
Given equation 5x – 12 = 0 in Z13.
Hence, it is required to find an element x such that
(5x-12) mod 13 = 0
Since, 0 = (m*13) mod 13 hence, 5x -12 = 13m
Now, xϵ {0,1,2,3,4,5,6,7,8,9,10,11,12 }
Hence, 5x -12 ϵ {−12 ,−7 ,−2,3,8,13,18,23,28,33,38,43,48}
In the set there is only one number matching to the form 13m which is 13 that is for x = 1.
Hence, the solution of 5x – 12 = 0 in Z13 is x = 1.
Given, x^2 – x – 1 = 0 in Z11.
Thus it required to find an element x such that
(x^2 – x – 1) mod 11 = 0
Since, 0 = (m*11) mod 11 hence, (x^2 – x – 1) = 11m
Now, xϵ {0,1,2,3,4,5,6,7,8,9,10}
Hence, (x^2 – x – 1) ϵ {−1 ,−1,1,5,11,19,29,41,55,71,89 }

3COURSEWORK RESIT
Hence, in the set there are two numbers 11 and 55 which matches to the form 11m and hence
the solution set is xϵ {4,8 }.
4.
Given tree:
Algorithm:
Choose arbitrary node.
Compute weight of each branch connected to node.
While weight of each branch >= n/2 (n= total number of nodes in tree)
Move to the adjacent node with heaviest branch.
End While
Output final node.
Hence, in the set there are two numbers 11 and 55 which matches to the form 11m and hence
the solution set is xϵ {4,8 }.
4.
Given tree:
Algorithm:
Choose arbitrary node.
Compute weight of each branch connected to node.
While weight of each branch >= n/2 (n= total number of nodes in tree)
Move to the adjacent node with heaviest branch.
End While
Output final node.
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

4COURSEWORK RESIT
Steps:
Total nodes n = 18. Hence, n/2 = 18/2 = 9. Thus centroid found when all branches have
weights < 9 or <=8
1) Node 6 randomly chosen. Weights of branches = 3,1,1,13
2) Moving to heaviest node 3. Weights of braches = 6,2,3,6
Hence, node 3 is the centroid as all braches have weight < 9.
5.
Given graph:
Starting node: A
Algorithm: breath-first-search
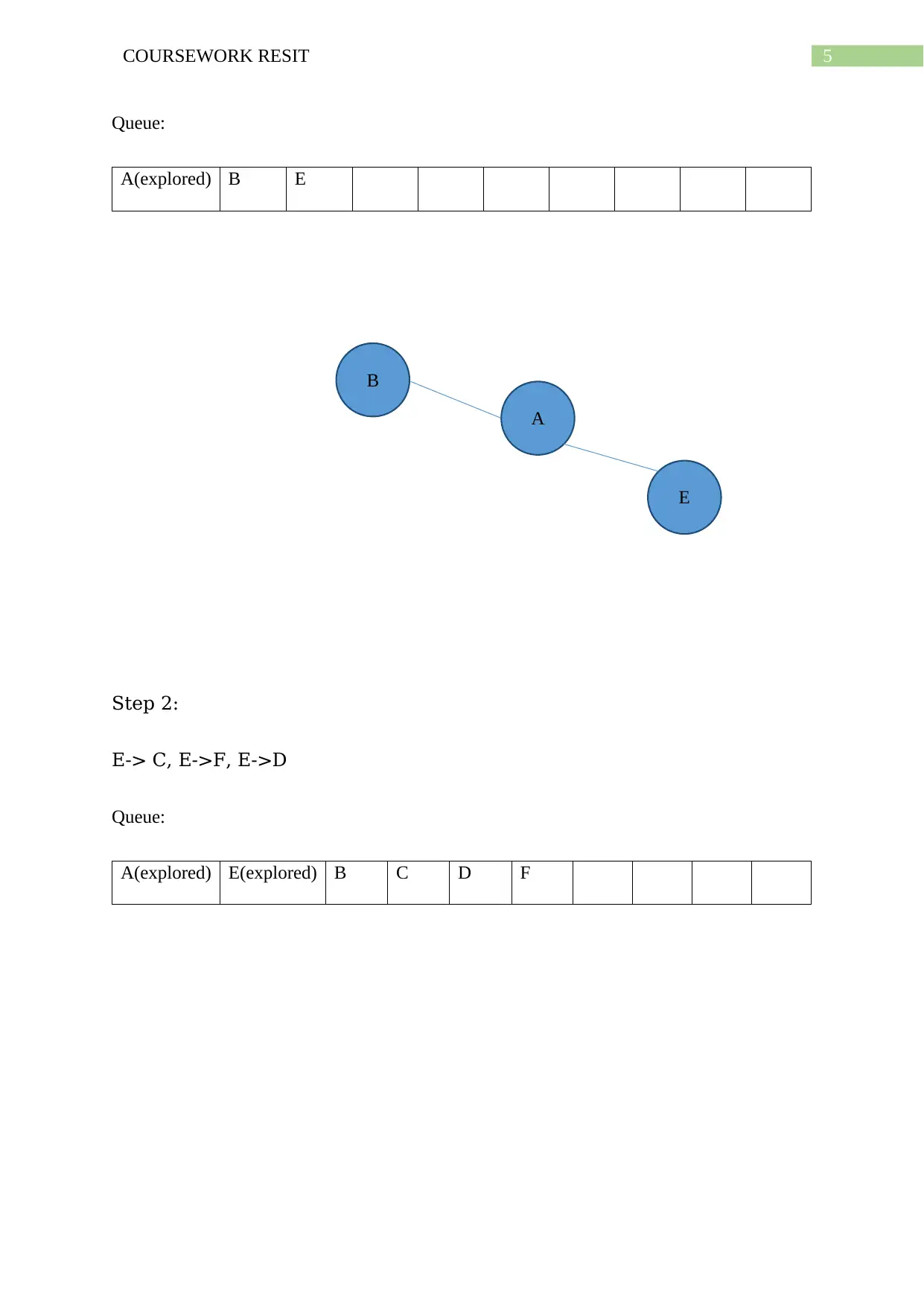
Step 1:
A -> B, A-> E
Steps:
Total nodes n = 18. Hence, n/2 = 18/2 = 9. Thus centroid found when all branches have
weights < 9 or <=8
1) Node 6 randomly chosen. Weights of branches = 3,1,1,13
2) Moving to heaviest node 3. Weights of braches = 6,2,3,6
Hence, node 3 is the centroid as all braches have weight < 9.
5.
Given graph:
Starting node: A
Algorithm: breath-first-search
Step 1:
A -> B, A-> E
5COURSEWORK RESIT
B
A
E
Queue:
A(explored) B E
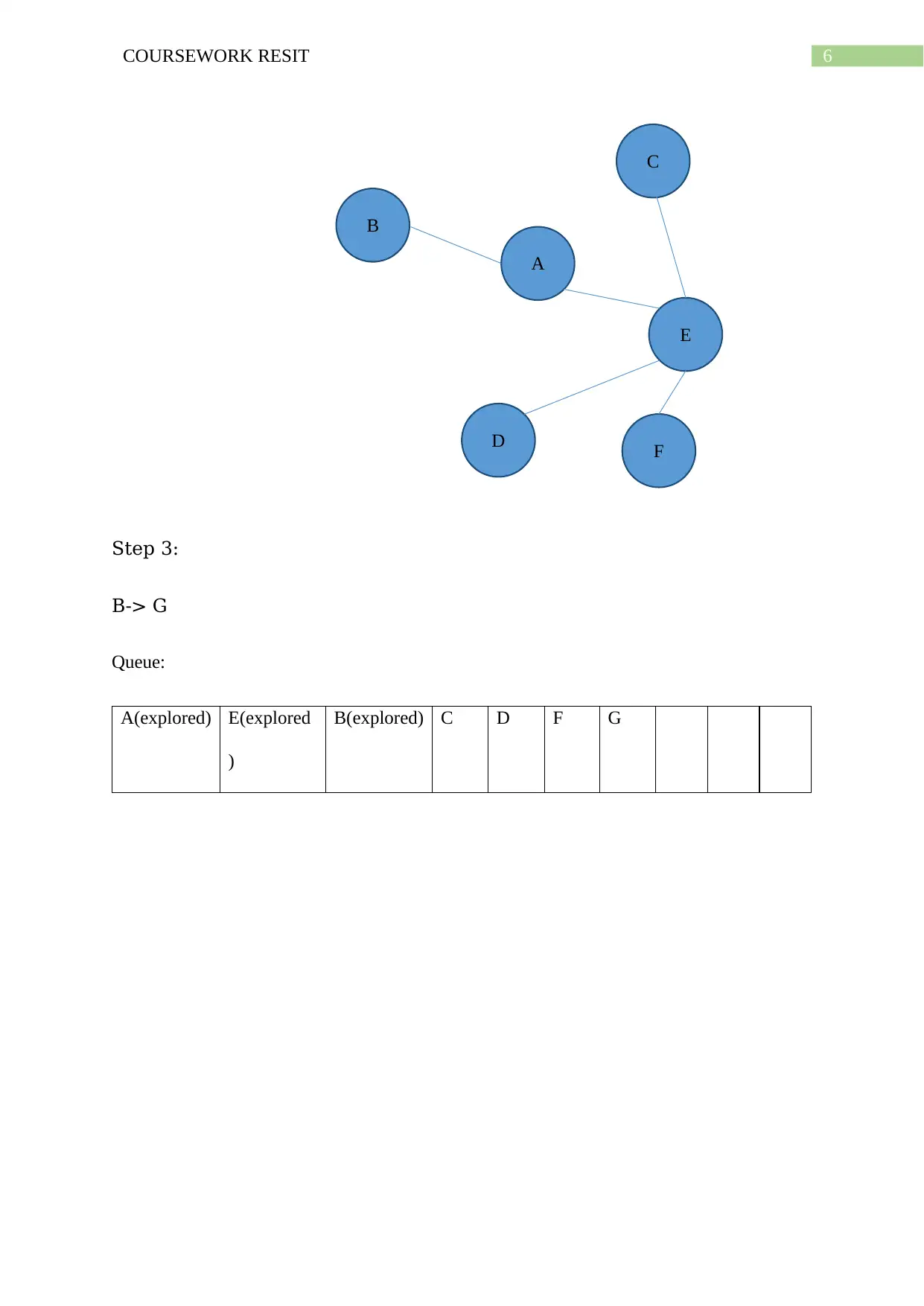
Step 2:
E-> C, E->F, E->D
Queue:
A(explored) E(explored) B C D F
B
A
E
Queue:
A(explored) B E
Step 2:
E-> C, E->F, E->D
Queue:
A(explored) E(explored) B C D F
6COURSEWORK RESIT
B
A
E
C
D F
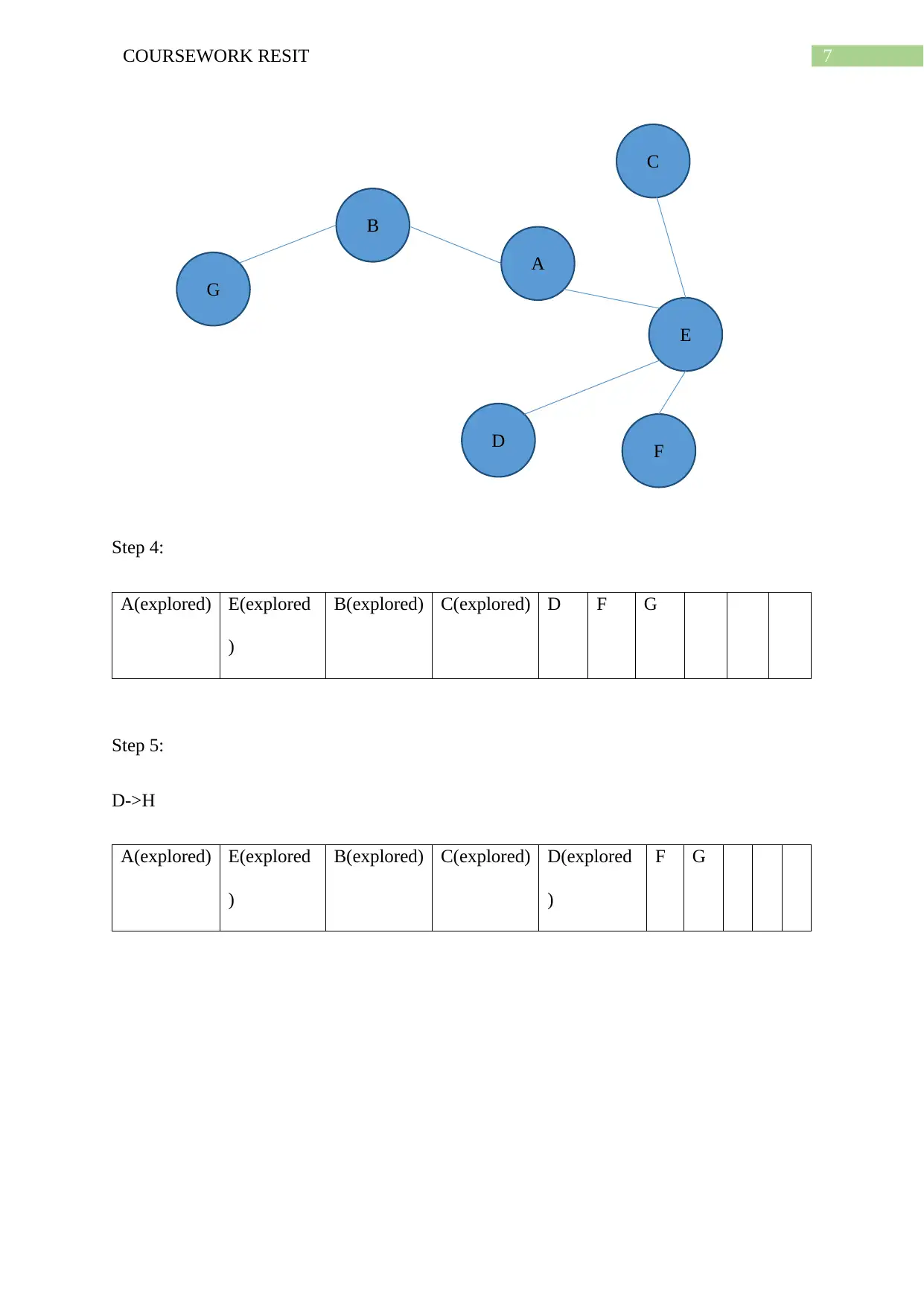
Step 3:
B-> G
Queue:
A(explored) E(explored
)
B(explored) C D F G
B
A
E
C
D F
Step 3:
B-> G
Queue:
A(explored) E(explored
)
B(explored) C D F G
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7COURSEWORK RESIT
B
A
E
C
D F
G
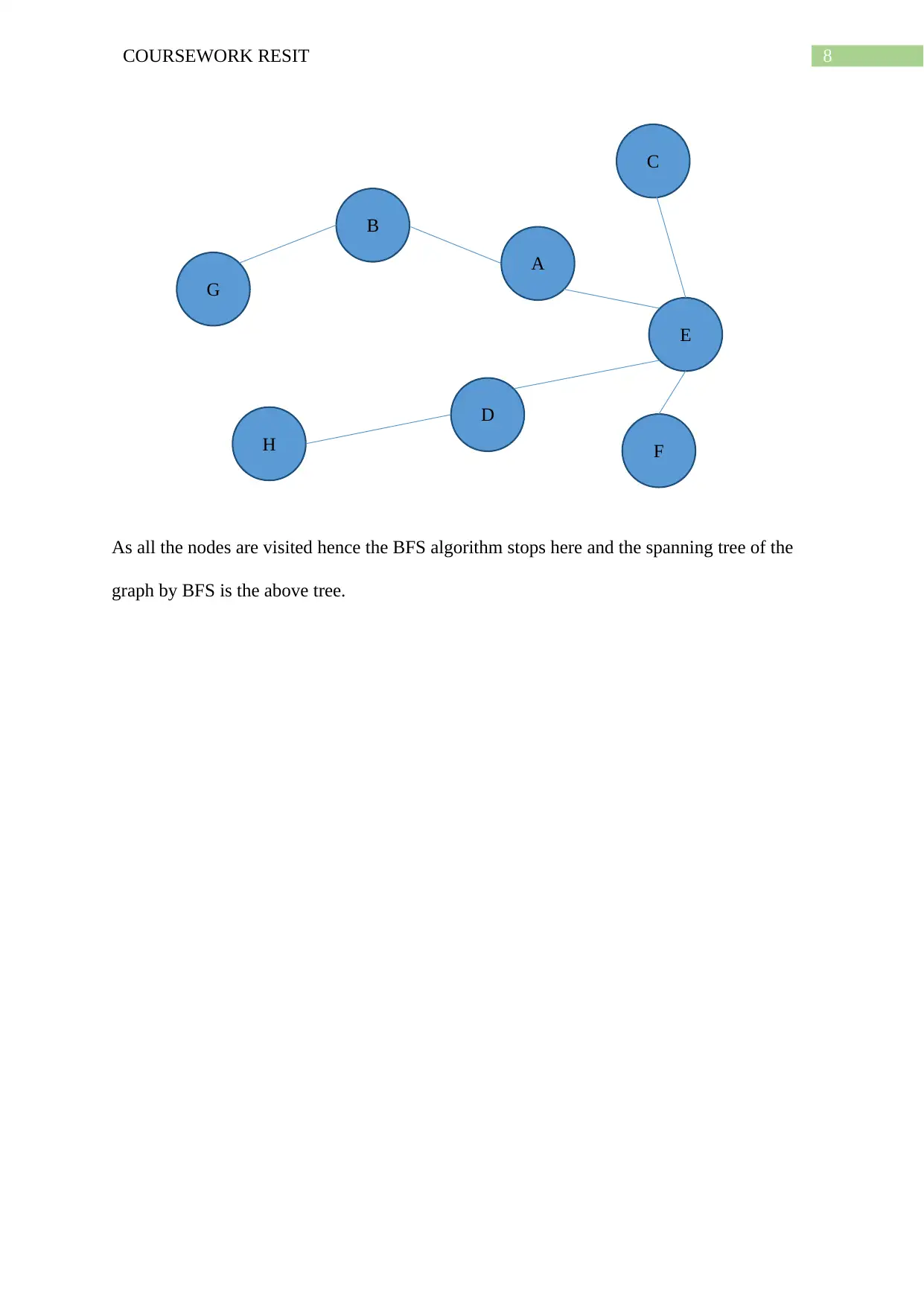
Step 4:
A(explored) E(explored
)
B(explored) C(explored) D F G
Step 5:
D->H
A(explored) E(explored
)
B(explored) C(explored) D(explored
)
F G
B
A
E
C
D F
G
Step 4:
A(explored) E(explored
)
B(explored) C(explored) D F G
Step 5:
D->H
A(explored) E(explored
)
B(explored) C(explored) D(explored
)
F G
8COURSEWORK RESIT
B
A
E
C
D
F
G
H
As all the nodes are visited hence the BFS algorithm stops here and the spanning tree of the
graph by BFS is the above tree.
B
A
E
C
D
F
G
H
As all the nodes are visited hence the BFS algorithm stops here and the spanning tree of the
graph by BFS is the above tree.
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.
