VietSteel's Transportation Improvement Plan and Cost Analysis Report

This report provides a comprehensive analysis of VietSteel Corporation's transportation challenges and proposes a plan for future improvement to optimize transportation costs. Due to increased demand, VietSteel faces the problem of outsourcing shipments and needs to find the most cost-effective shipping schedules. The analysis focuses on the Least Cost Method to find the initial feasible solution, followed by the Stepping-stone and Modified Distribution (MODI) methods to test for optimality. The report includes detailed calculations and insights, demonstrating how these methods can help VietSteel minimize transportation expenses and maximize profitability. The findings reveal that the initial feasible solution is optimal, with multiple shipment schedules available at the same cost. The report recommends using the MODI method for faster evaluation and provides alternative shipping plans. This analysis aims to help VietSteel's transportation manager make informed decisions and improve the company's operational efficiency.

1
(COVER PAGE)

2
TABLE of CONTENTS
EXECUTIVE SUMMANY.......................................................................................................................3
I. INTRODUCTION.............................................................................................................................4
II. PROBLEM STATEMENT...........................................................................................................4
III. ANALYSIS & DISCUSSION........................................................................................................5
a. ANALYSIS.....................................................................................................................................5
b. DISCUSSION...............................................................................................................................13
IV. CONCLUSION............................................................................................................................13
V. REFERENCES................................................................................................................................15

3
EXECUTIVE SUMMANY
The paper is about the future improvement plan that VietSteel’s transportation manager would
deliver to support the company having an optimal transportation cost, which could contribute to
the company’s profitability. The issue here is the significant rising demand for steel products,
and VietSteel must outsource their overloaded shipments. It is the manager’s task to balance the
demand and supply capacity between shipping points and destinations while still ensure
maximum profitability.
The first section of the paper addresses briefly about VietSteel’s challenge. The second section,
which is the highlight of the paper, is an analysis of steps on how to solve VietSteel’s challenge.
There are two steps: step one is to find the initial feasible solution/ initial basic feasible solution
using the “Least Cost method”; step two is to test the optimality of step one to see whether exists
a better solution or not, using the “Stepping-stone method” and the “Modified Distribution
(MODI) method”. This section provides detailed insights and calculations for each approach
used to help readers understand how the transportation manager came to a conclusion, and how
are those three approaches would assist VietSteel in solving their current problem.
Notably, the result obtained is that the initial feasible solution is optimal. VietSteel will have a
total of four shipment schedules to choose, whereas still endure to the same transportation fee of
$6,950. Furthermore, different shipment allocations equivalent with their schedule are presented
as well.
It is suggested that after determining the initial feasible solution, the transportation manager
should use mathematical equations of the MODI method instead of using the traditional
calculations of the Stepping-stone method to reduce solving time

4
I. INTRODUCTION
Inexpensive transportation costs are what any business would strike to (Buu Dien 2015)
associated with high availability as they allow firms to be more responsive to demands regarding
accurate and punctual shipping schedules (Russell et al. 2014). However, high transportation
expenses have been a burden to the logistic industry in Vietnam, as well as the whole economy
since they have occupied 40% to 60% of total logistics costs (Saigon Times 2018). VietSteel
Corporation, a Vietnamese producer and distributor of steel products located in Vietnam, is
experiencing the same challenge.
The paper will present different methods conducted by VietSteel’s transportation manager which
would assist the company in arranging shipping schedule effectively and accurately
II. PROBLEM STATEMENT
Due to the recent increase of demand, VietSteel’s truck fleet is operating over capacity and now
must outsource their excessive shipping requirements to third-party transportation firms. The
addressed problem here is that the company must find a way not only to allocate their shipping
order wisely to ensure accurate material availability between destinations but also to bear a
minimal transportation cost. According to Deep, Jain and Salhi (2019), VietSteel is facing a
problem called a “Transportation Problem (TP)”, which deals with optimal distribution from
several sources to different destinations while still maintaining minimal total cost, demand as
well as capacity constraints.

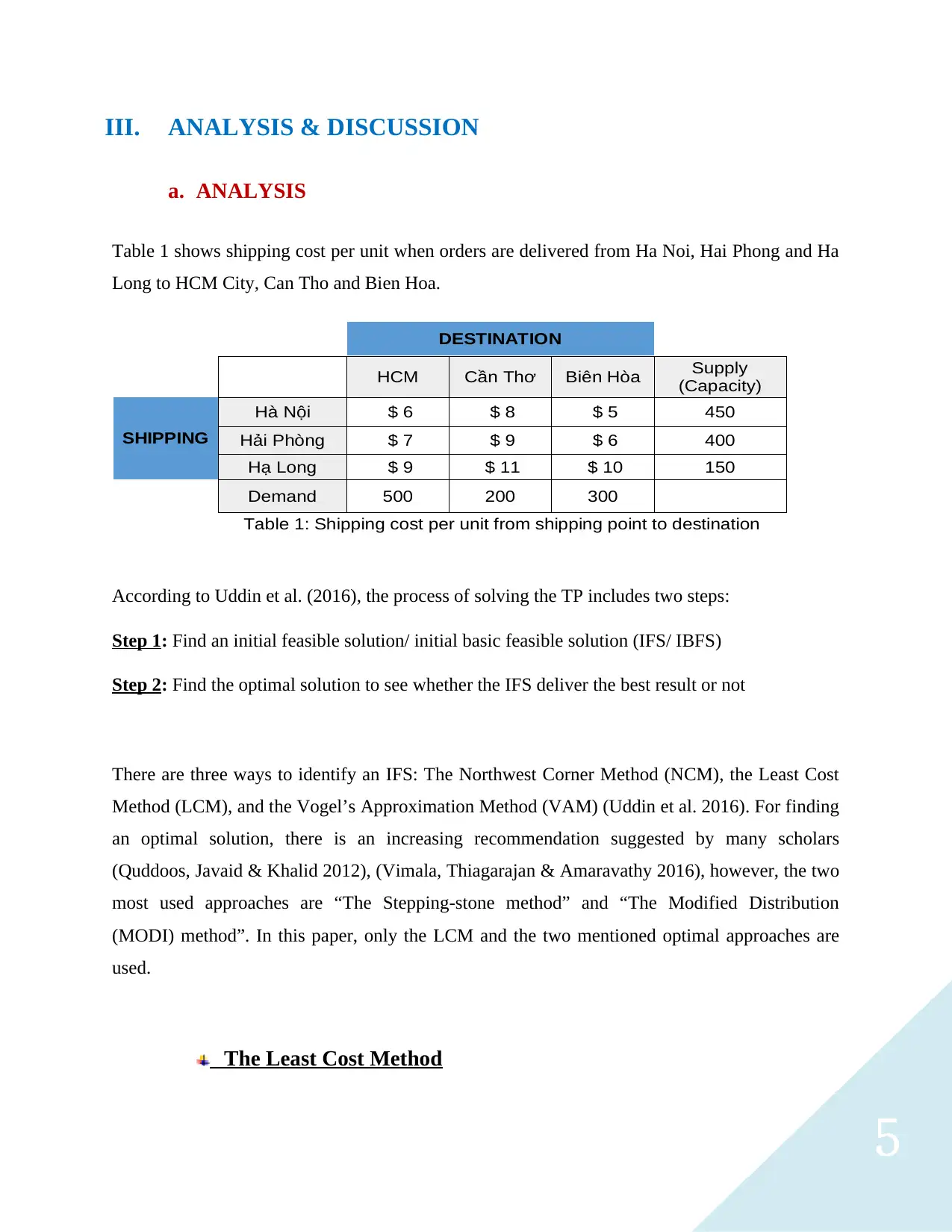
5
DESTINATION
HCM Cần Thơ Biên Hòa Supply
(Capacity)
SHIPPING
Hà Nội $ 6 $ 8 $ 5 450
Hải Phòng $ 7 $ 9 $ 6 400
Hạ Long $ 9 $ 11 $ 10 150
Demand 500 200 300
Table 1: Shipping cost per unit from shipping point to destination
III. ANALYSIS & DISCUSSION
a. ANALYSIS
Table 1 shows shipping cost per unit when orders are delivered from Ha Noi, Hai Phong and Ha
Long to HCM City, Can Tho and Bien Hoa.
According to Uddin et al. (2016), the process of solving the TP includes two steps:
Step 1: Find an initial feasible solution/ initial basic feasible solution (IFS/ IBFS)
Step 2: Find the optimal solution to see whether the IFS deliver the best result or not
There are three ways to identify an IFS: The Northwest Corner Method (NCM), the Least Cost
Method (LCM), and the Vogel’s Approximation Method (VAM) (Uddin et al. 2016). For finding
an optimal solution, there is an increasing recommendation suggested by many scholars
(Quddoos, Javaid & Khalid 2012), (Vimala, Thiagarajan & Amaravathy 2016), however, the two
most used approaches are “The Stepping-stone method” and “The Modified Distribution
(MODI) method”. In this paper, only the LCM and the two mentioned optimal approaches are
used.
The Least Cost Method

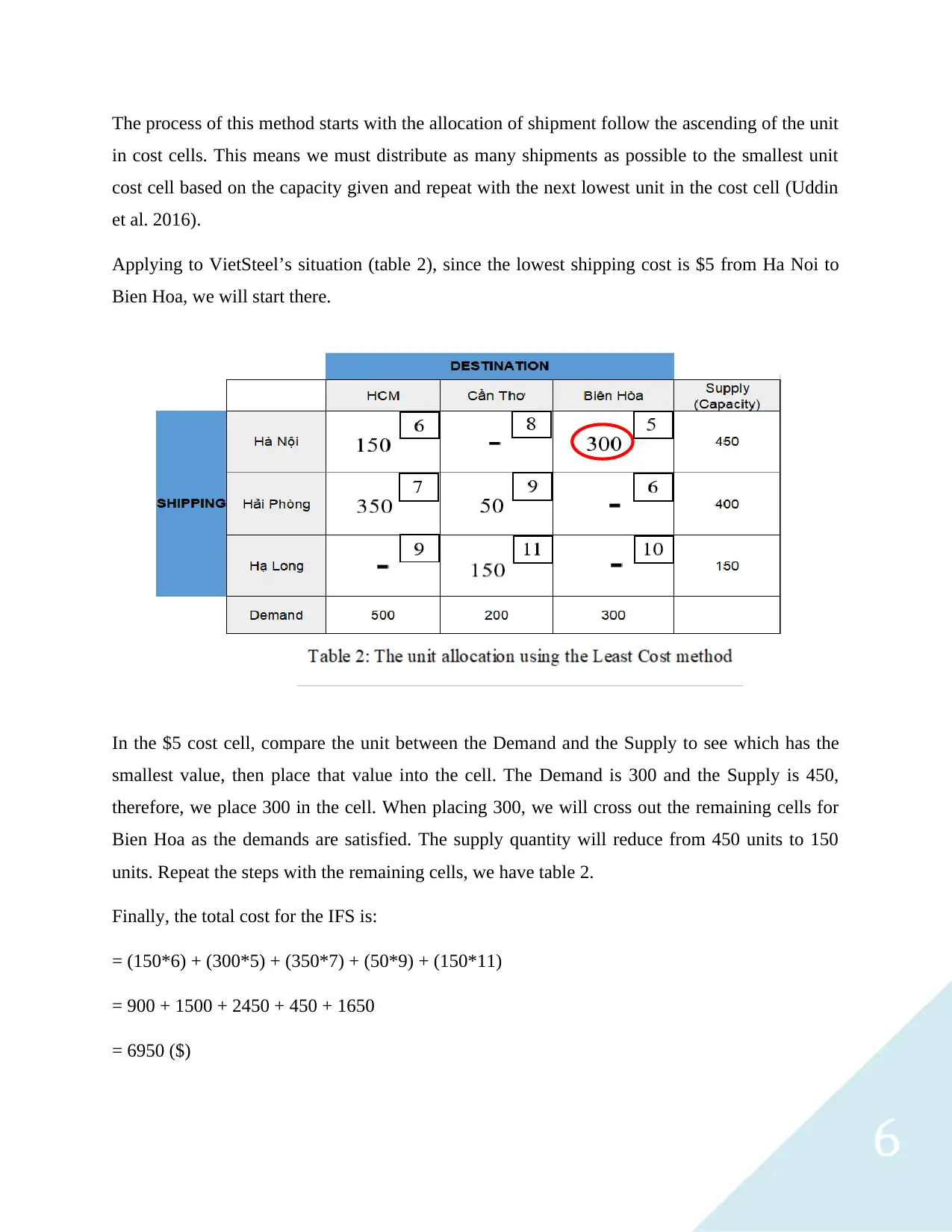
6
The process of this method starts with the allocation of shipment follow the ascending of the unit
in cost cells. This means we must distribute as many shipments as possible to the smallest unit
cost cell based on the capacity given and repeat with the next lowest unit in the cost cell (Uddin
et al. 2016).
Applying to VietSteel’s situation (table 2), since the lowest shipping cost is $5 from Ha Noi to
Bien Hoa, we will start there.
In the $5 cost cell, compare the unit between the Demand and the Supply to see which has the
smallest value, then place that value into the cell. The Demand is 300 and the Supply is 450,
therefore, we place 300 in the cell. When placing 300, we will cross out the remaining cells for
Bien Hoa as the demands are satisfied. The supply quantity will reduce from 450 units to 150
units. Repeat the steps with the remaining cells, we have table 2.
Finally, the total cost for the IFS is:
= (150*6) + (300*5) + (350*7) + (50*9) + (150*11)
= 900 + 1500 + 2450 + 450 + 1650
= 6950 ($)

7
After finding the IFS, we will test its optimality using the two methods below to see whether
there are better alternative solutions.
The Stepping-stone Method
This method exams the optimality of the IFS by evaluating the potential of unoccupied cells to
see if they produce a better cost minimization (Dansereau 2012). Supposedly, one unit will be
placed in each empty cell and proceed row by row (Shih 1987).
Step 1: Select an empty cell and add one unit to it by placing “+”
Step 2: From the selected empty cell, create a closed path via the occupied cell, and the endpoint
is the initial empty cell. In this step:
 Only use horizontal and vertical path
 The path must make a turn at an occupied cell
Step 3: After forming a path, place “-” (leaving) and “+” (entering) respectively to balance the
Demand and Supply
Step 4: Calculate the net value (Z) by adding and subtracting the cost according to the “+”, “-”
signs placed.
 If Z > 0  it is costly to change the shipment route  Eliminated
 If Z = 0  the optimality is unchanged (Can proceed to step 5 if there are no smaller
values)
 If Z < 0  it is optimal to change the shipment route  Proceed to step 5
Step 5: Select the smallest net value and exam the “-” cells in the path again, compare them and
select the smallest “-” cell, then place that value in each cell that forms a path.
Step 6: Calculate the new variables

8
Apply the steps to VietSteel’s case, we have table 3.1, table 4.1, table 5.1 and table 6.1. The net
value for each table is:
 Table 3.1 (from Ha Noi to Can
Tho):
Z = + 8 - 6 + 7 - 9
Z = 0
 Table 4.1 (from Hai Phong to Bien
Hoa):
Z = + 6 -5 + 6 - 7
Z = 0
 Table 5.1 (from Ha Long to HCM):
Z = + 9 - 11 + 9 - 7
Z = 0
 Table 6.1 (from Ha Long to Bien
Hoa):
Z = + 10 - 5 + 6 - 7 + 9 - 11
Z = 2
Based on the result, delivery changes made in the first three mentioned table consent with the
optimality of the IFS. Nonetheless, the shipment change in table 6.1 suggests a higher expense,
hence is eliminated.
Then, we compare the “leaving” cell in each remaining table. For table 3.1, 50 units is the
smallest value, so we place 50 in each cell that forms a path (table 3.2). As a result, we have new
variables as well as another option for changing the shipment route illustrated in table 3.3.
Repeat these steps we have the remaining tables (4.2, 4.3, 5.2, 5.3). As a result, VietSteel obtains
two more alternative shipping plans which still reserve the initial optimal cost ($6950)

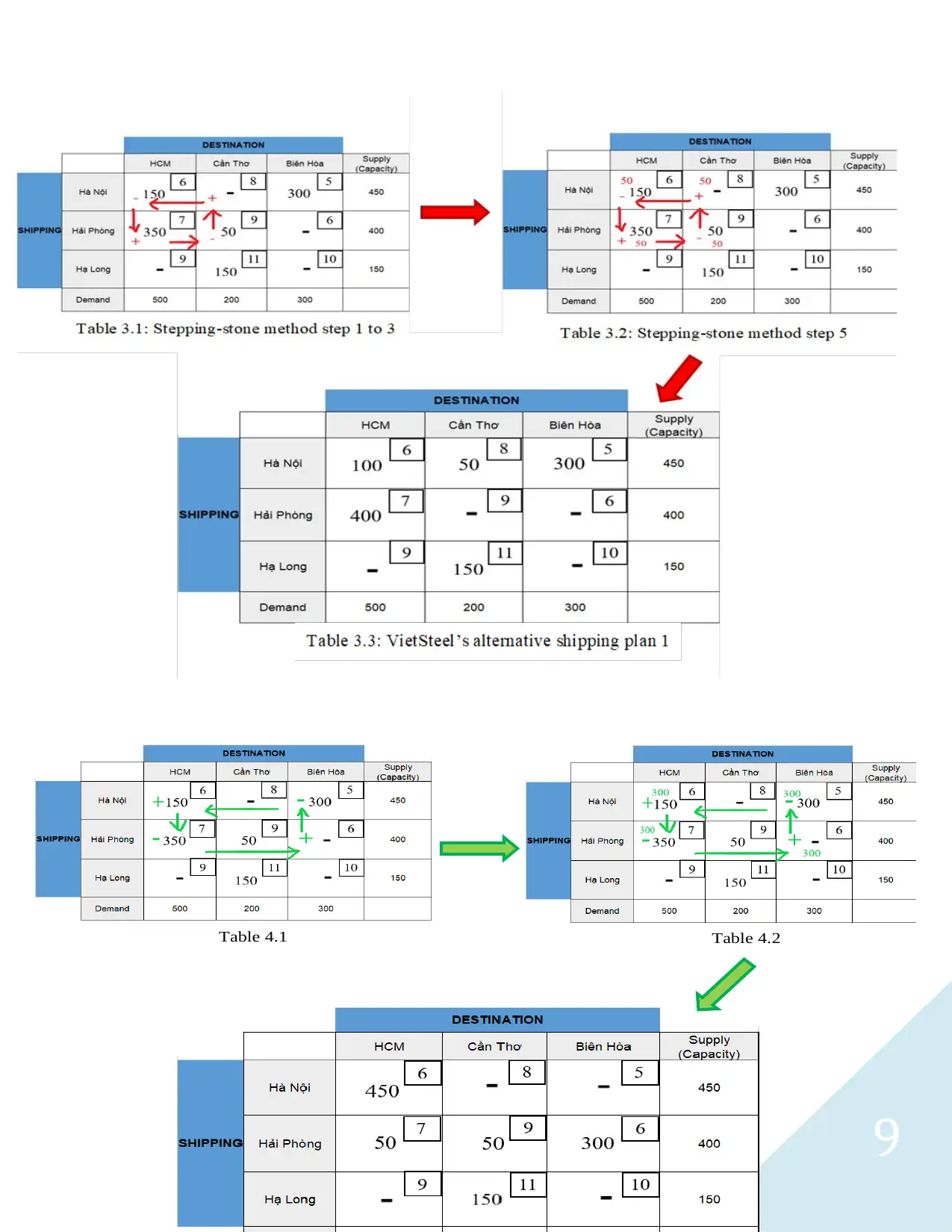
9
Table 4.1 Table 4.2

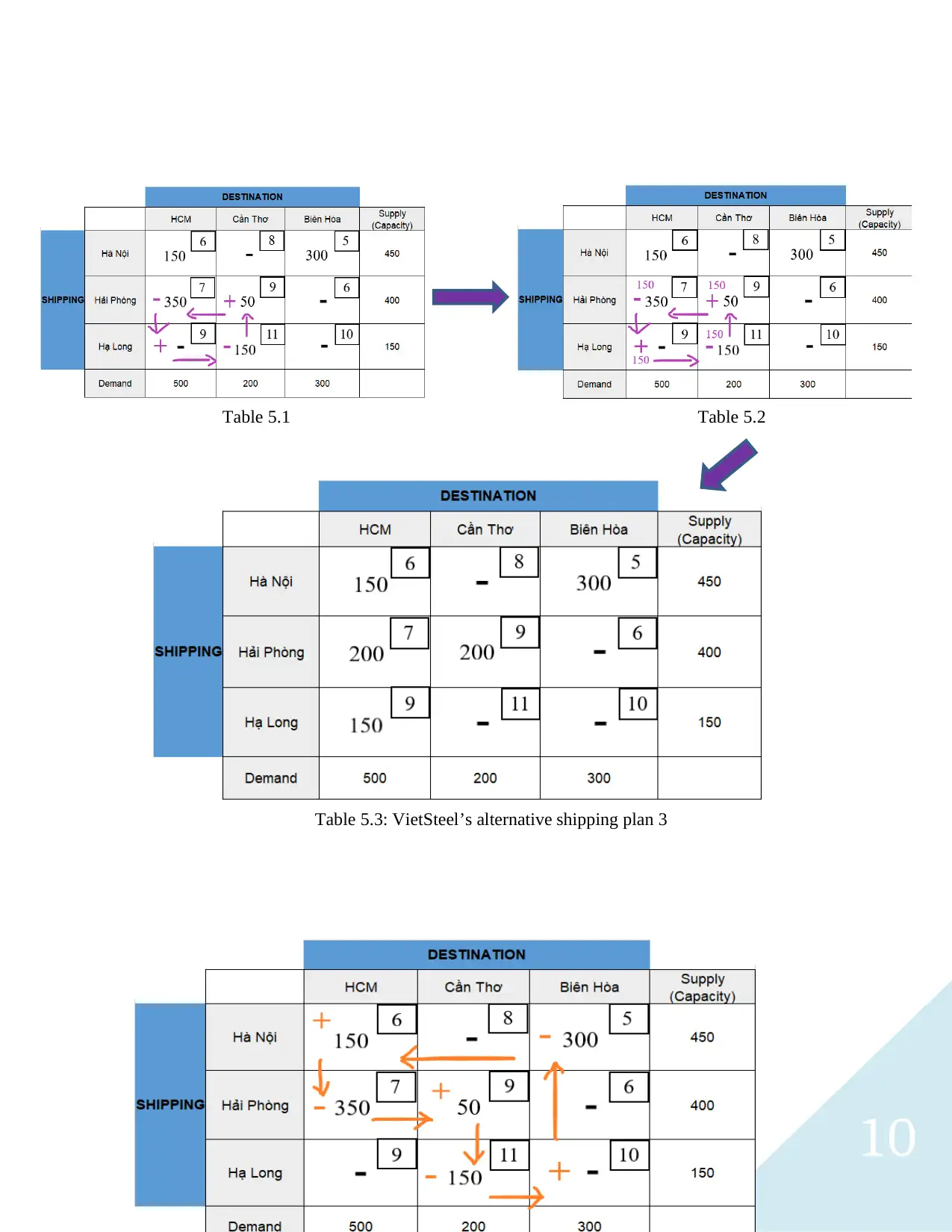
10
Table 5.1
Table 5.3: VietSteel’s alternative shipping plan 3
Table 5.2

11
Modified Distribution Method (MODI)
According to Limbore and Chandrakant (2013), there are two explanations. Firstly, this is an
advanced method of the Stepping-stone approach since it replaces the stone path with
mathematical equations, therefore, provide a much faster evaluation process. Secondly, the
method will exam unused cells as well, however, forming a path for each unused cell is
unnecessary.
Step 1: Place U as each shipping source and V as each destination
Step 2: Calculate each U and V using the equation C12 = U1 + V2. ONLY use C from occupied
cell
Step 3: Calculate the net value (Z) using the equation Z12 = C12 – U1 – V2 on empty cells
 If Z > 0  it is costly to change the shipment route  Eliminated
 If Z = 0  the optimality is unchanged (Can proceed to step 4 if there are no smaller
values)
 If Z < 0  it is optimal to change the shipment route  Proceed to step 4
Step 4: Use the Stepping-stone method on the smallest net value obtained
Apply to VietSteel’s case, we have table 7. Firstly, U1, U2, U3 represents Ha Noi, Hai Phong, and
Ha Long respectively. V1, V2, V3 represents HCM, Can Tho, and Bien Hoa respectively.
Secondly, place U1 = 0, then use the equation C12 = U1 + V2 to determine the remaining U and V,
we have:
 C11 = U1 + V1
6 = 0 + V1
 V1 = 6 - 0 = 6
 C21 = U2 + V1
7 = U2 + 6

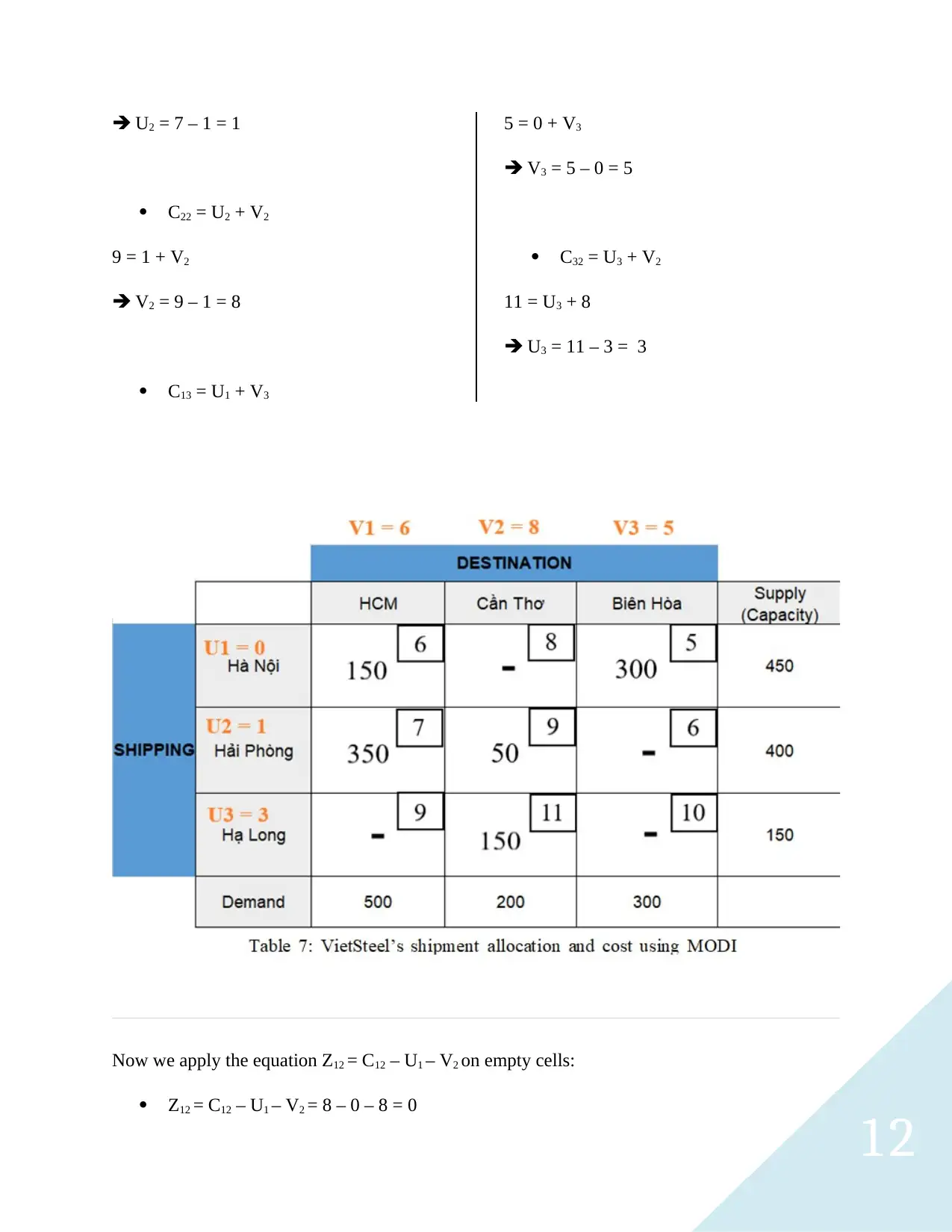
12
 U2 = 7 – 1 = 1
 C22 = U2 + V2
9 = 1 + V2
 V2 = 9 – 1 = 8
 C13 = U1 + V3
5 = 0 + V3
 V3 = 5 – 0 = 5
 C32 = U3 + V2
11 = U3 + 8
 U3 = 11 – 3 = 3
Now we apply the equation Z12 = C12 – U1 – V2 on empty cells:
 Z12 = C12 – U1 – V2 = 8 – 0 – 8 = 0