DMU ENGT5258/ENGD5258 Advanced Solid Mechanics: Creep & Fatigue
VerifiedAdded on 2023/05/30
|7
|831
|220
Homework Assignment
AI Summary
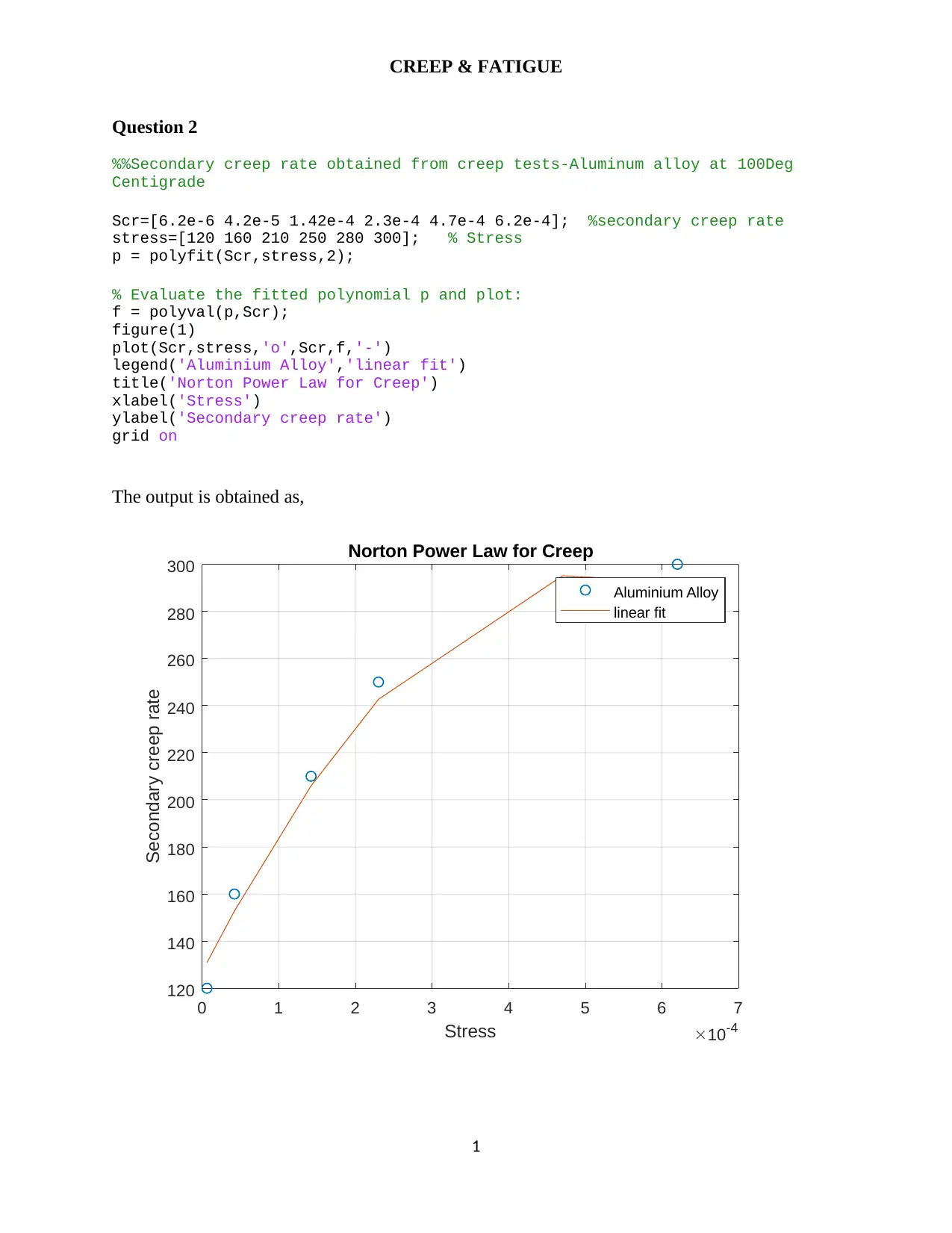
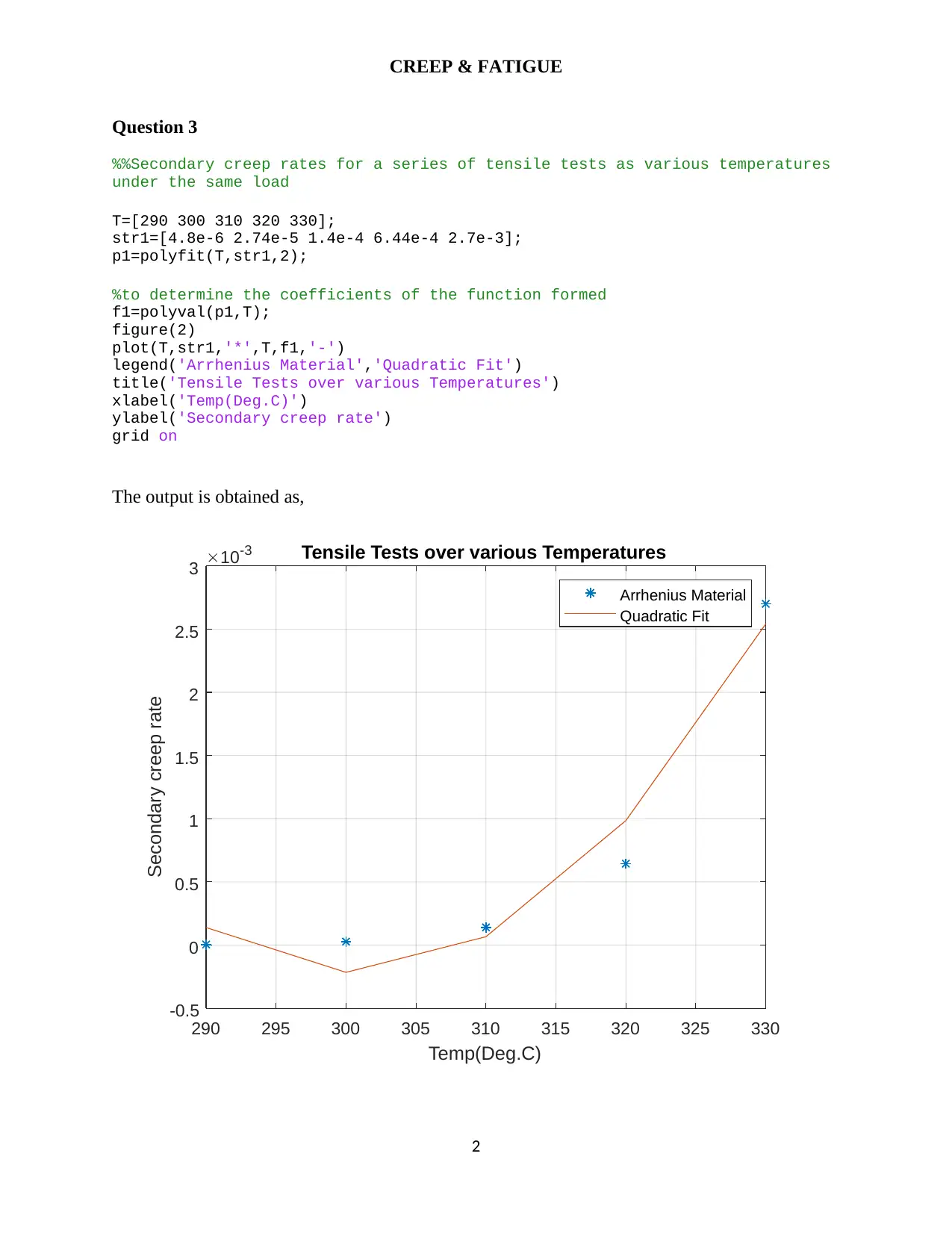
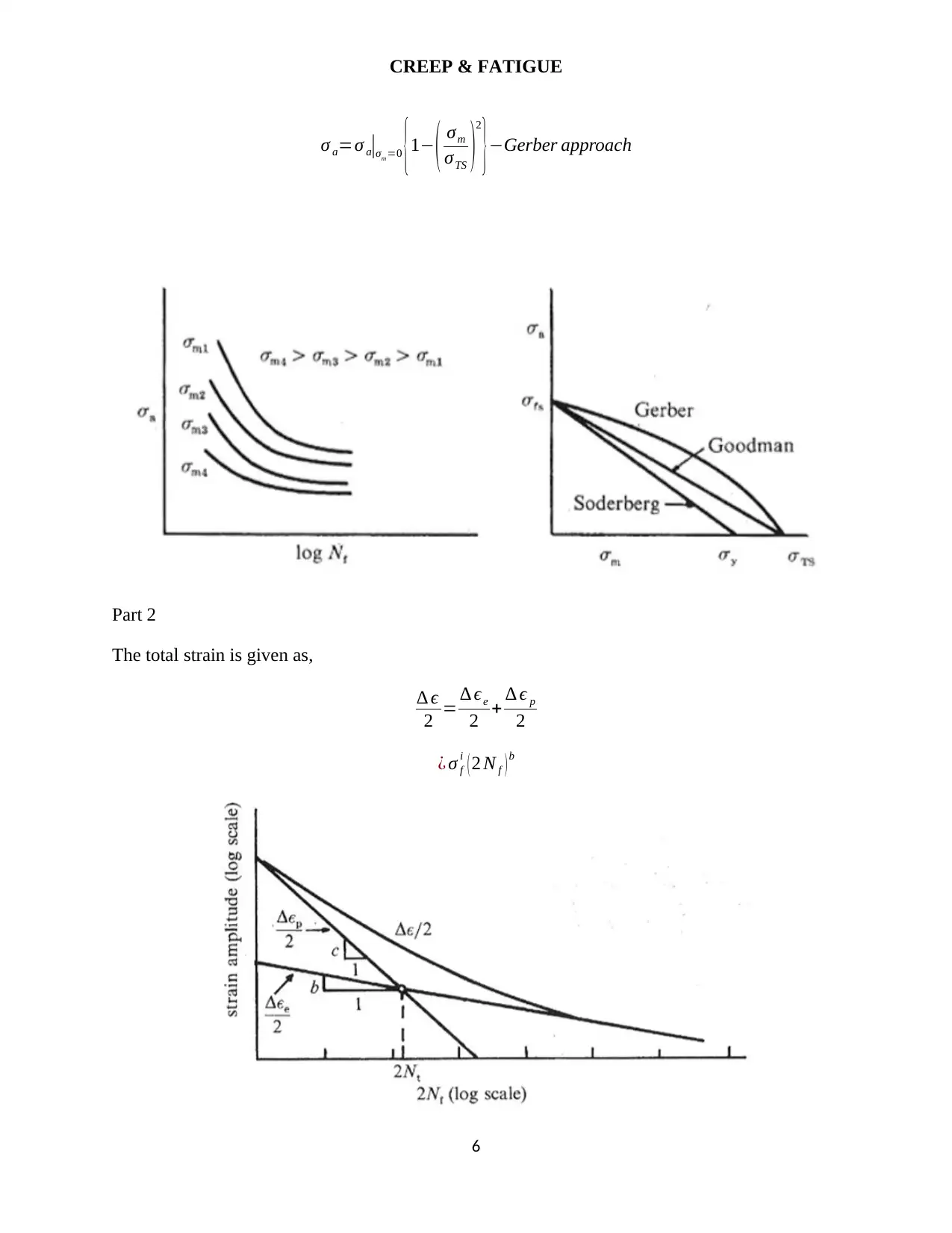
This assignment focuses on creep and fatigue analysis within the context of advanced solid mechanics, specifically addressing questions related to creep rates, tensile tests at varying temperatures, and fatigue life prediction. It includes calculations for creep relaxation in cylindrical vessels, determination of time to re-tighten bolts, and application of Miner's rule for fatigue life assessment. The assignment also covers safe stress range calculations using Gerber and Goodman fatigue predictions. The solutions presented involve the application of Norton's power law, Arrhenius material models, and Weibull distribution for life characteristics. This document is available on Desklib, a platform offering a wide range of study tools and resources for students.
1 out of 7






![[object Object]](/_next/static/media/star-bottom.7253800d.svg)