Mechanical Engineering: Heat Transfer Problem - Critical Insulation
VerifiedAdded on 2023/06/03
|6
|823
|449
Homework Assignment
AI Summary
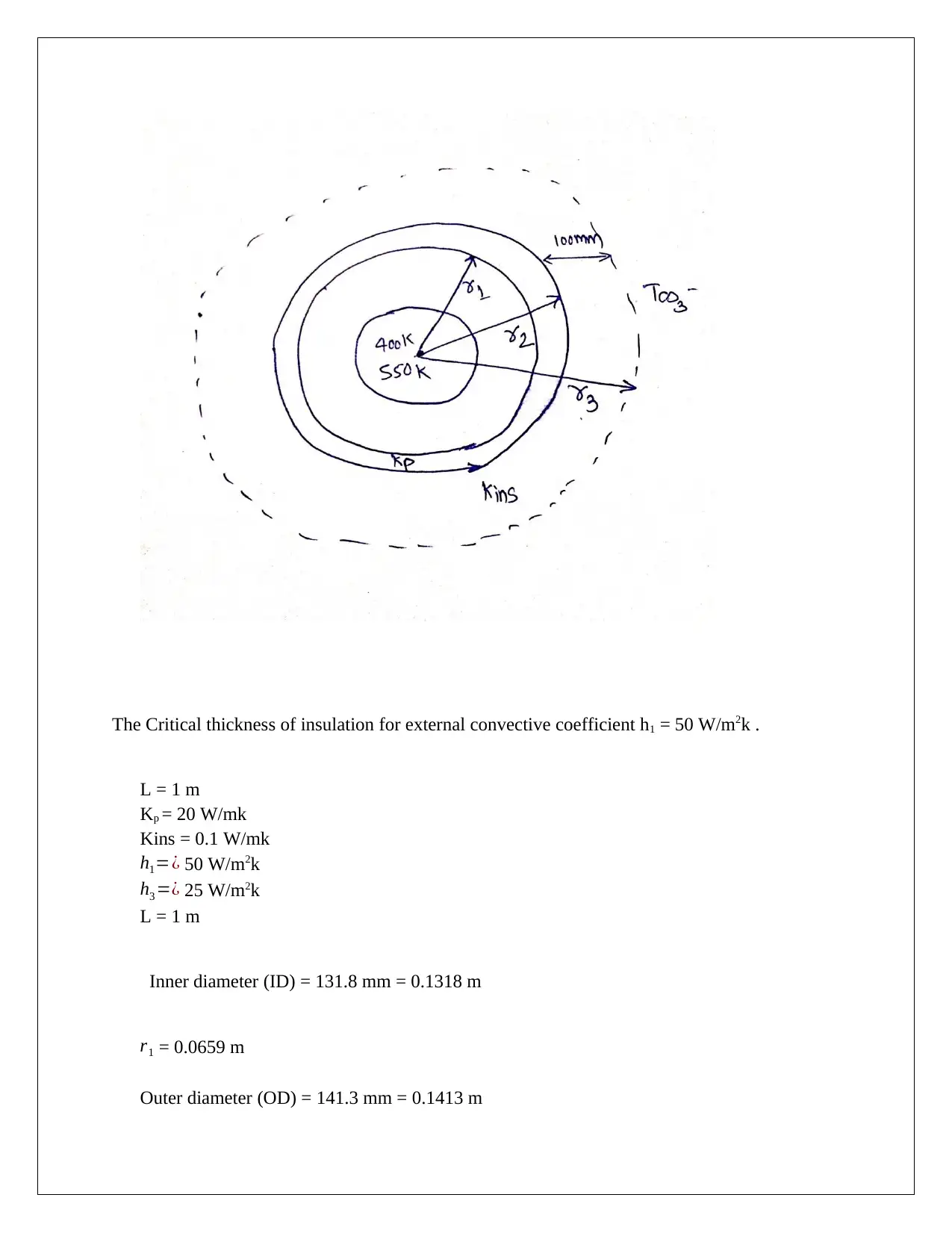
This assignment addresses a heat transfer problem concerning the critical radius of insulation for a cylindrical pipe. The problem defines a scenario where a pipe with a constant surface temperature is insulated with a material of known thermal conductivity, and the surrounding medium is at a lower temperature with a given convective heat transfer coefficient. The solution begins with defining the problem, making necessary assumptions (fixed insulation thickness, negligible air gaps, radiation losses, and series resistances), and applying engineering principles. It explains that for wires with a radius less than the critical radius of insulation, adding insulation can initially increase the heat transfer rate due to a decrease in convection resistance. The core of the solution involves calculating the critical thickness of insulation using given parameters (pipe dimensions, thermal conductivities, and convective heat transfer coefficients). It then calculates the heat transfer rate per meter of pipe with and without insulation, demonstrating how the addition of insulation beyond the critical thickness reduces heat loss. References to relevant literature are also included, supporting the analysis and providing context to the problem-solving approach.
1 out of 6












![[object Object]](/_next/static/media/star-bottom.7253800d.svg)