Data Analysis Report: Statistical Analysis of GPA and Insurance Models
VerifiedAdded on 2020/03/23
|16
|2057
|325
Report
AI Summary
This report presents a comprehensive data analysis, beginning with an investigation into the relationship between first-year GPA and undergraduate GPA using linear regression. The analysis includes the examination of box plots to visualize GPA distributions and the application of t-tests to compare GPA scores. The report then transitions to a decision tree analysis, evaluating insurance policies for a Chevrolet Lacetti in Turkey. This section calculates Expected Monetary Value (EMV) for different insurance scenarios, including no insurance, liability insurance, and liability with collision insurance, to determine the optimal insurance strategy. Furthermore, the report explores the impact of a deductible policy and compares decision trees with simulations, highlighting the advantages of decision trees in strategic planning. The report concludes with a bibliography of relevant sources.

Running head: DATA ANALYSIS
Data Analysis
Name of the Student:
Name of the University:
Author Note:
Data Analysis
Name of the Student:
Name of the University:
Author Note:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

DATA ANALYSIS 1
Table of Contents
Question 1......................................................................................................................................................2
Question 2......................................................................................................................................................9
Part a).........................................................................................................................................................9
Part b).......................................................................................................................................................10
Part c).......................................................................................................................................................13
Part d).......................................................................................................................................................14
Bibliography:...............................................................................................................................................15
Table of Contents
Question 1......................................................................................................................................................2
Question 2......................................................................................................................................................9
Part a).........................................................................................................................................................9
Part b).......................................................................................................................................................10
Part c).......................................................................................................................................................13
Part d).......................................................................................................................................................14
Bibliography:...............................................................................................................................................15

DATA ANALYSIS 2
Question 1
The linear regression model between First year GPA and the Undergraduate GPA of MAB:
Call:
lm(formula = Undergrad.GPA ~ First.Year.GPA, data = result)
Residuals:
Min 1Q Median 3Q Max
-0.8654 -0.2587 -0.0265 0.2495 0.8868
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.89323 0.26943 7.027 3.75e-10 ***
First.Year.GPA 0.31109 0.07974 3.901 0.000183 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3771 on 91 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.1433, Adjusted R-squared: 0.1339
Question 1
The linear regression model between First year GPA and the Undergraduate GPA of MAB:
Call:
lm(formula = Undergrad.GPA ~ First.Year.GPA, data = result)
Residuals:
Min 1Q Median 3Q Max
-0.8654 -0.2587 -0.0265 0.2495 0.8868
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.89323 0.26943 7.027 3.75e-10 ***
First.Year.GPA 0.31109 0.07974 3.901 0.000183 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3771 on 91 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.1433, Adjusted R-squared: 0.1339
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

DATA ANALYSIS 3
F-statistic: 15.22 on 1 and 91 DF, p-value: 0.0001831
The linear regression model is given by-
Undergrad.GPA = 1.89323 + 0.31109* FirstYearGPA.
The very little value of multiple R-square (0.1433) shows that there is a very little linear
relationship between the values First Year GPA and Undergraduate GPA. The larger value of F-statistic
than the p-value interprets that the null hypothesis of assuming the linear relationship between these two
factors is not accepted.
The box plot of the students who have GPA less than 3 at the end of 2 years course of
Undergraduate:
F-statistic: 15.22 on 1 and 91 DF, p-value: 0.0001831
The linear regression model is given by-
Undergrad.GPA = 1.89323 + 0.31109* FirstYearGPA.
The very little value of multiple R-square (0.1433) shows that there is a very little linear
relationship between the values First Year GPA and Undergraduate GPA. The larger value of F-statistic
than the p-value interprets that the null hypothesis of assuming the linear relationship between these two
factors is not accepted.
The box plot of the students who have GPA less than 3 at the end of 2 years course of
Undergraduate:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

DATA ANALYSIS 4
Figure 1: A box plot shows the distribution of GPA who achieved less than 3 at under graduation.
summary(Undergraduate)
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.200 2.500 2.650 2.624 2.800 2.980
The summary plot of GPA of Undergraduate passed students shows that the median of the GPA
score is 2.650 and mean of GPA score is 2.624.
Next, our main aim is to find the students’ summary who has gotten less than GPA 3 at the end of
first year. These students are in the probation period at the end of the first year.
summary(Probation)
Figure 1: A box plot shows the distribution of GPA who achieved less than 3 at under graduation.
summary(Undergraduate)
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.200 2.500 2.650 2.624 2.800 2.980
The summary plot of GPA of Undergraduate passed students shows that the median of the GPA
score is 2.650 and mean of GPA score is 2.624.
Next, our main aim is to find the students’ summary who has gotten less than GPA 3 at the end of
first year. These students are in the probation period at the end of the first year.
summary(Probation)
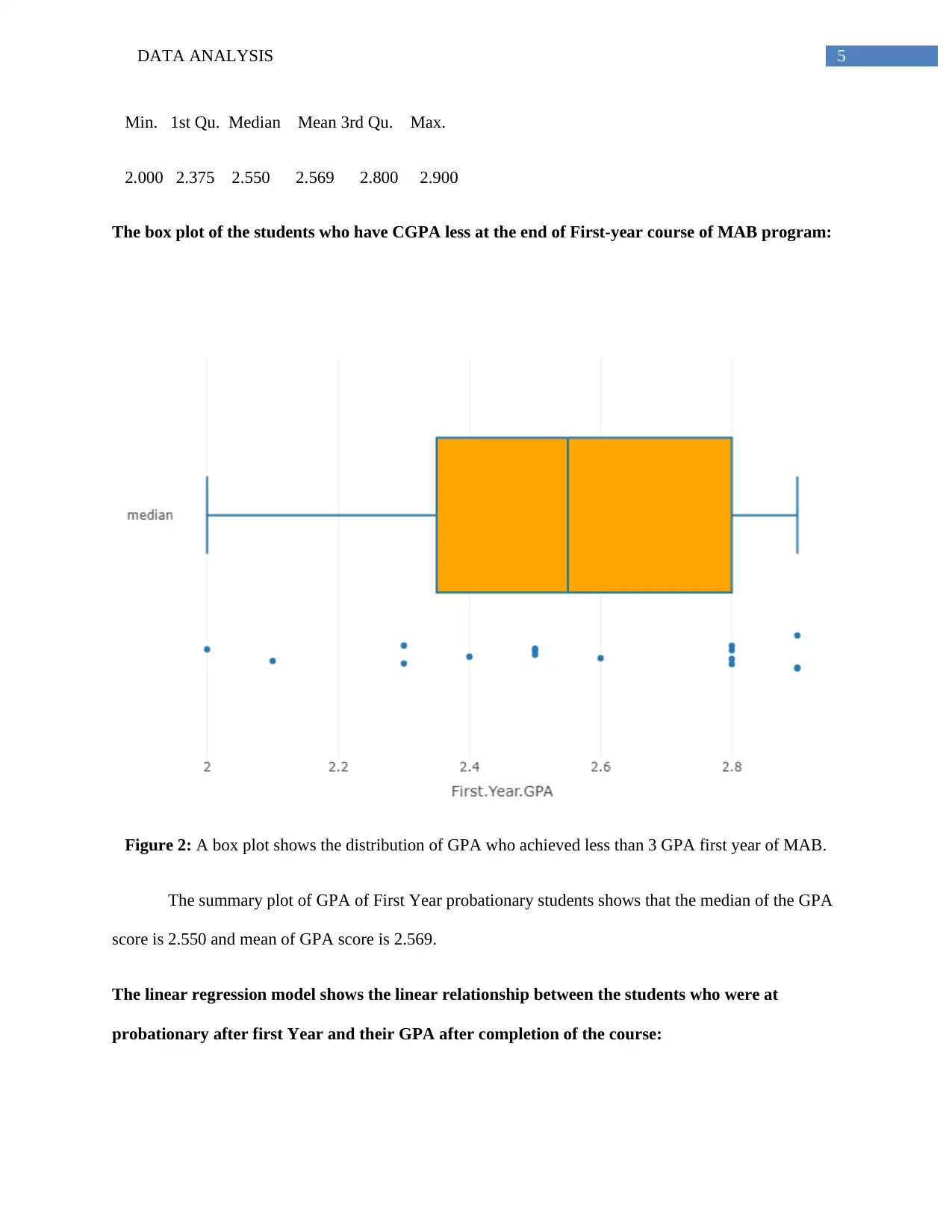
DATA ANALYSIS 5
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.000 2.375 2.550 2.569 2.800 2.900
The box plot of the students who have CGPA less at the end of First-year course of MAB program:
Figure 2: A box plot shows the distribution of GPA who achieved less than 3 GPA first year of MAB.
The summary plot of GPA of First Year probationary students shows that the median of the GPA
score is 2.550 and mean of GPA score is 2.569.
The linear regression model shows the linear relationship between the students who were at
probationary after first Year and their GPA after completion of the course:
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.000 2.375 2.550 2.569 2.800 2.900
The box plot of the students who have CGPA less at the end of First-year course of MAB program:
Figure 2: A box plot shows the distribution of GPA who achieved less than 3 GPA first year of MAB.
The summary plot of GPA of First Year probationary students shows that the median of the GPA
score is 2.550 and mean of GPA score is 2.569.
The linear regression model shows the linear relationship between the students who were at
probationary after first Year and their GPA after completion of the course:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

DATA ANALYSIS 6
Call:
lm(formula = FirstYearGPA ~ UndergraduateGPA)
Residuals:
Min 1Q Median 3Q Max
-0.61803 -0.19790 -0.02867 0.25553 0.35998
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.9938 0.6287 4.762 0.000304 ***
UndergraduateGPA -0.1592 0.2339 -0.681 0.507121
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2968 on 14 degrees of freedom
Multiple R-squared: 0.03204, Adjusted R-squared: -0.0371
F-statistic: 0.4634 on 1 and 14 DF, p-value: 0.5071
AIC(LinearModel.1)
[1] 10.40283
In this case, the linear regression model is =
FirstYearGPA = 2.9938 - 0.1592*UndergraduateGPA.
Call:
lm(formula = FirstYearGPA ~ UndergraduateGPA)
Residuals:
Min 1Q Median 3Q Max
-0.61803 -0.19790 -0.02867 0.25553 0.35998
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.9938 0.6287 4.762 0.000304 ***
UndergraduateGPA -0.1592 0.2339 -0.681 0.507121
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2968 on 14 degrees of freedom
Multiple R-squared: 0.03204, Adjusted R-squared: -0.0371
F-statistic: 0.4634 on 1 and 14 DF, p-value: 0.5071
AIC(LinearModel.1)
[1] 10.40283
In this case, the linear regression model is =
FirstYearGPA = 2.9938 - 0.1592*UndergraduateGPA.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
DATA ANALYSIS 7
The Value of F- statistic is less than its p-value. Therefore, we not reject the linear relationship
between the GPA score of First Year and GPA of Undergraduate. Therefore, in spite of very little value
of multiple R square, we cannot deny the insignificant relationship between these two factors.
cor(FirstYearGPA,UndergraduateGPA)
[1] -0.1790048
The correlation coefficient between these factors is (-0.1790048). Therefore, we find a negative
insignificant correlation between these two factors.
Histogram of UndergraduateGPA who were
at probition after first Year
UndergraduateGPA
F r e q u e n c y
2.2 2.4 2.6 2.8 3.0 3.2 3.4
0 1 2 3 4
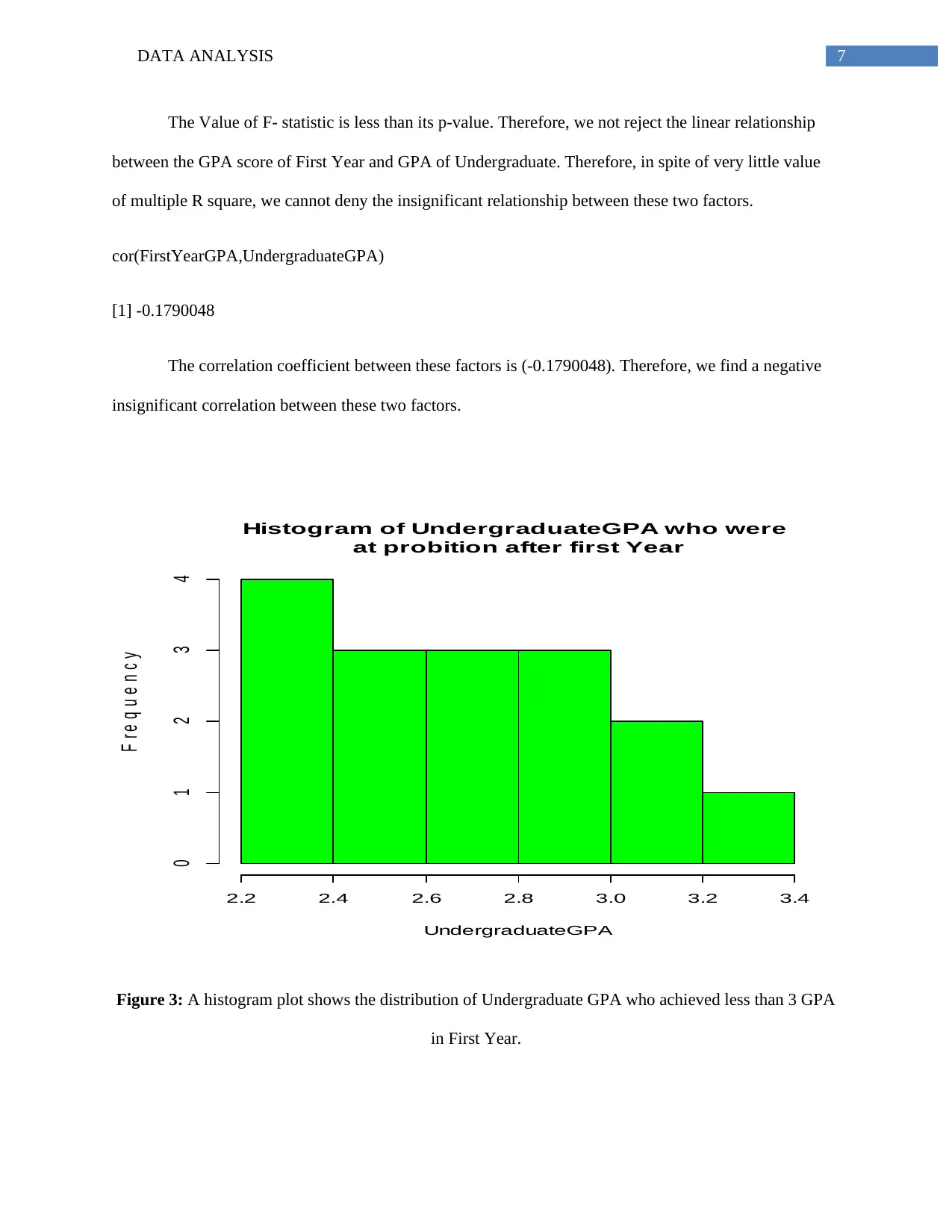
Figure 3: A histogram plot shows the distribution of Undergraduate GPA who achieved less than 3 GPA
in First Year.
The Value of F- statistic is less than its p-value. Therefore, we not reject the linear relationship
between the GPA score of First Year and GPA of Undergraduate. Therefore, in spite of very little value
of multiple R square, we cannot deny the insignificant relationship between these two factors.
cor(FirstYearGPA,UndergraduateGPA)
[1] -0.1790048
The correlation coefficient between these factors is (-0.1790048). Therefore, we find a negative
insignificant correlation between these two factors.
Histogram of UndergraduateGPA who were
at probition after first Year
UndergraduateGPA
F r e q u e n c y
2.2 2.4 2.6 2.8 3.0 3.2 3.4
0 1 2 3 4
Figure 3: A histogram plot shows the distribution of Undergraduate GPA who achieved less than 3 GPA
in First Year.

DATA ANALYSIS 8
The histogram shows that among the first year probationary student of frequency 16, only 3
students got more than 3 GPA at the end of two years course. The other 13 students who were at
probation, still count not was able to qualify the final Undergraduate exam.
The Two Sample t-tests between comparison of two GPA score:
t.test(FirstYearGPA,UndergraduateGPA)
Welch Two Sample t-test
data: FirstYearGPA and UndergraduateGPA
t = -0.9191, df = 29.597, p-value = 0.3655
Alternative hypothesis: true difference in means is not equal to 0
95% confidence interval:
-0.3248278 0.1232778
sample estimates:
mean of x mean of y
2.568750 2.669525
The two-sample t-test shows the value of t-statistic = (-0.9191). It is less than the calculated p-
value (0.3655). Not only that the value of t-statistic does not lie between the 95% confidence interval (-
0.3248278, 0.1232778). Therefore, the null hypothesis of equal means is not rejected here.
Suggestion of other model and its validity:
The histogram shows that among the first year probationary student of frequency 16, only 3
students got more than 3 GPA at the end of two years course. The other 13 students who were at
probation, still count not was able to qualify the final Undergraduate exam.
The Two Sample t-tests between comparison of two GPA score:
t.test(FirstYearGPA,UndergraduateGPA)
Welch Two Sample t-test
data: FirstYearGPA and UndergraduateGPA
t = -0.9191, df = 29.597, p-value = 0.3655
Alternative hypothesis: true difference in means is not equal to 0
95% confidence interval:
-0.3248278 0.1232778
sample estimates:
mean of x mean of y
2.568750 2.669525
The two-sample t-test shows the value of t-statistic = (-0.9191). It is less than the calculated p-
value (0.3655). Not only that the value of t-statistic does not lie between the 95% confidence interval (-
0.3248278, 0.1232778). Therefore, the null hypothesis of equal means is not rejected here.
Suggestion of other model and its validity:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

DATA ANALYSIS 9
We assumed linear regression model to correlate these factors. Nevertheless, the linear
relationship between these two factors is not properly correlated. We also applied two-sample t-test for
equal mean of GPA of these 2 samples.
Now, if we are interested in applying another statistical model, we can apply multiple regression
models. Here, we cannot apply multiple regression model, because, the two factors are numeric and
discrete in nature.
We cannot use “logit” models also. It is a particular type of multiple regression model because,
the model needs as regressor only categorical and dichotomous variables. In case of Genaralised Linear
Model (GLM), we cannot proceed for singular discrete nature of both the factors. Therefore, inverse
gamma model cannot be implemented here also because, these two factors have no interaction effect.
Lastly, we can proceed to apply Joint Generalised Linear Model (JGLM). This can be a proper
choice of application. We can apply Gamma model or log-linear model to have a better result.
Question 2
Part a)
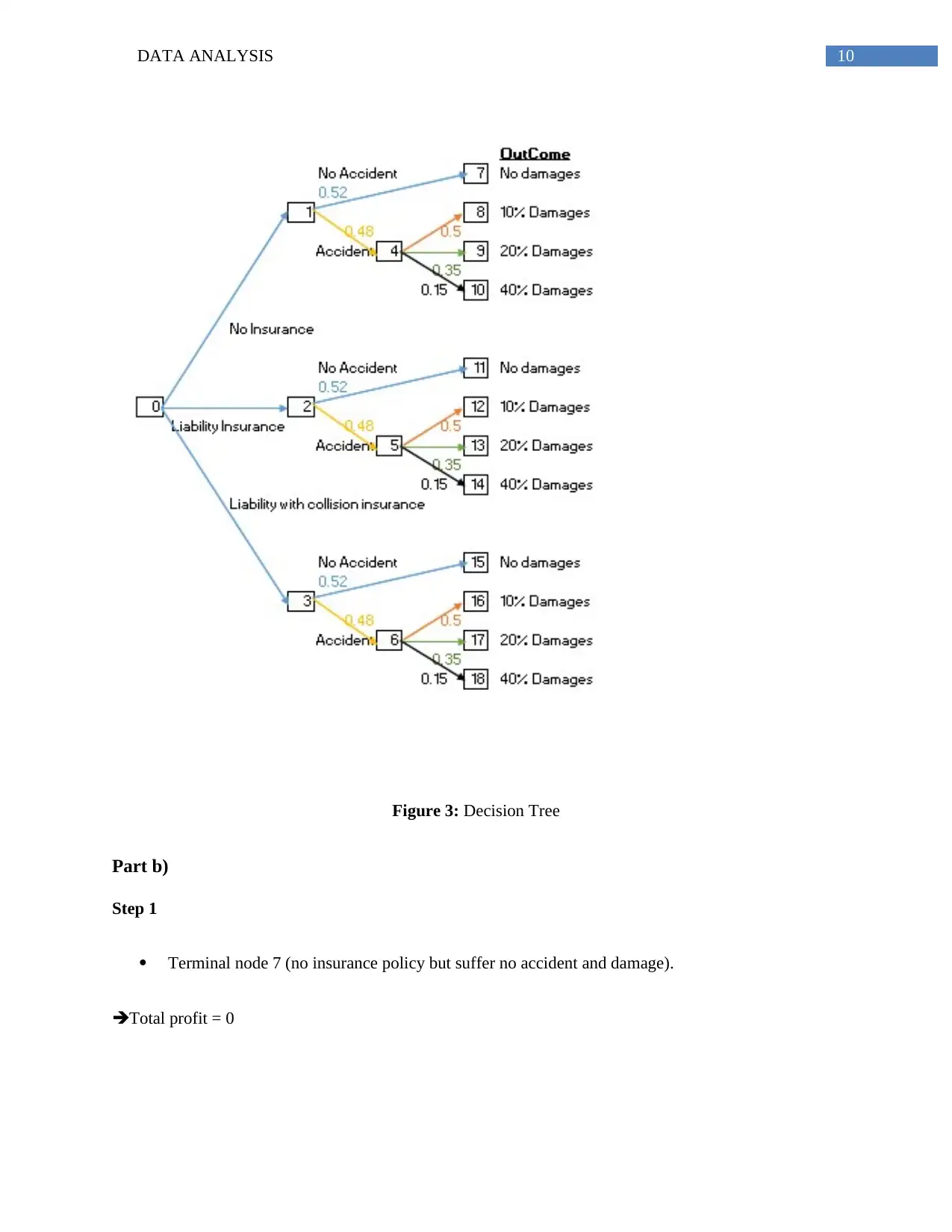
Car chosen for the analysis is Chevrolet Lacetti in Turkey
Book Value = £89390
Turkey’s car accident rate is 48% and no accident is 52%.
The decision tree for the model is given as:
We assumed linear regression model to correlate these factors. Nevertheless, the linear
relationship between these two factors is not properly correlated. We also applied two-sample t-test for
equal mean of GPA of these 2 samples.
Now, if we are interested in applying another statistical model, we can apply multiple regression
models. Here, we cannot apply multiple regression model, because, the two factors are numeric and
discrete in nature.
We cannot use “logit” models also. It is a particular type of multiple regression model because,
the model needs as regressor only categorical and dichotomous variables. In case of Genaralised Linear
Model (GLM), we cannot proceed for singular discrete nature of both the factors. Therefore, inverse
gamma model cannot be implemented here also because, these two factors have no interaction effect.
Lastly, we can proceed to apply Joint Generalised Linear Model (JGLM). This can be a proper
choice of application. We can apply Gamma model or log-linear model to have a better result.
Question 2
Part a)
Car chosen for the analysis is Chevrolet Lacetti in Turkey
Book Value = £89390
Turkey’s car accident rate is 48% and no accident is 52%.
The decision tree for the model is given as:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
DATA ANALYSIS 10
Figure 3: Decision Tree
Part b)
Step 1
Terminal node 7 (no insurance policy but suffer no accident and damage).
Total profit = 0
Figure 3: Decision Tree
Part b)
Step 1
Terminal node 7 (no insurance policy but suffer no accident and damage).
Total profit = 0

DATA ANALYSIS 11
Terminal node 8 (no insurance policy but suffer a accident resulting in a damage of 10% of the
car.
Total cost = 0.1(89390) = 8939
Total profit = - 8,939
Terminal nodes 9 and 10
Total profit for node 9= -17,878
Total profit for node 10 = -35,756
Terminal node 11 (Liability Insurance policy) costing £670 but suffer no damages.
Total cost = 670
Total profit = -670
Terminal node 12 (Liability insurance policy) costing £670 but suffer a damage resulting in a loss
of 0.1(89390) = £8939 for which we are reimbursed in full by liability insurance during accident.
Total revenue = 8939
Total cost = 8939 + 670 ; Total profit = -670
From calculation Reimbursement = Amount Lost (total profit = cost of the insurance).
Same is for terminal nodes 13 and 14 respectively.
Such as a table can be derived as:
Terminal node Total profit £
7 0
Terminal node 8 (no insurance policy but suffer a accident resulting in a damage of 10% of the
car.
Total cost = 0.1(89390) = 8939
Total profit = - 8,939
Terminal nodes 9 and 10
Total profit for node 9= -17,878
Total profit for node 10 = -35,756
Terminal node 11 (Liability Insurance policy) costing £670 but suffer no damages.
Total cost = 670
Total profit = -670
Terminal node 12 (Liability insurance policy) costing £670 but suffer a damage resulting in a loss
of 0.1(89390) = £8939 for which we are reimbursed in full by liability insurance during accident.
Total revenue = 8939
Total cost = 8939 + 670 ; Total profit = -670
From calculation Reimbursement = Amount Lost (total profit = cost of the insurance).
Same is for terminal nodes 13 and 14 respectively.
Such as a table can be derived as:
Terminal node Total profit £
7 0
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 16
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





