Data Analysis and Forecasting

This study explores data analysis and forecasting techniques, including mean, median, range, and standard deviation. It also covers linear forecasting and its application in making predictions. The importance of descriptive data analysis is highlighted.

Data Analysis and Forecasting

TABLE OF CONTENTS
TABLE OF CONTENTS................................................................................................................2
REFERENCES................................................................................................................................8

INTRODUTION
Data analysis and forecasting is an effective procedure to analyse and effectively make
appropriate set of predictions on the basis of present and past data and analysing the key relevant
trends. This study will highlight on evaluating the wide data sets using appropriate data analysis
technique.
TASK
1. Creating a table for the data related to phone calls
Sr. No. Date
Phone calls
per day
1 01-07-2020 2
2 02-07-2020 6
3 03-07-2020 5
4 04-07-2020 8
5 05-07-2020 4
6 06-07-2020 7
7 07-07-2020 9
8 08-07-2020 5
9 09-07-2020 8
10 10-07-2020 5
2. Presentation of data for phone calls in graphical format
1

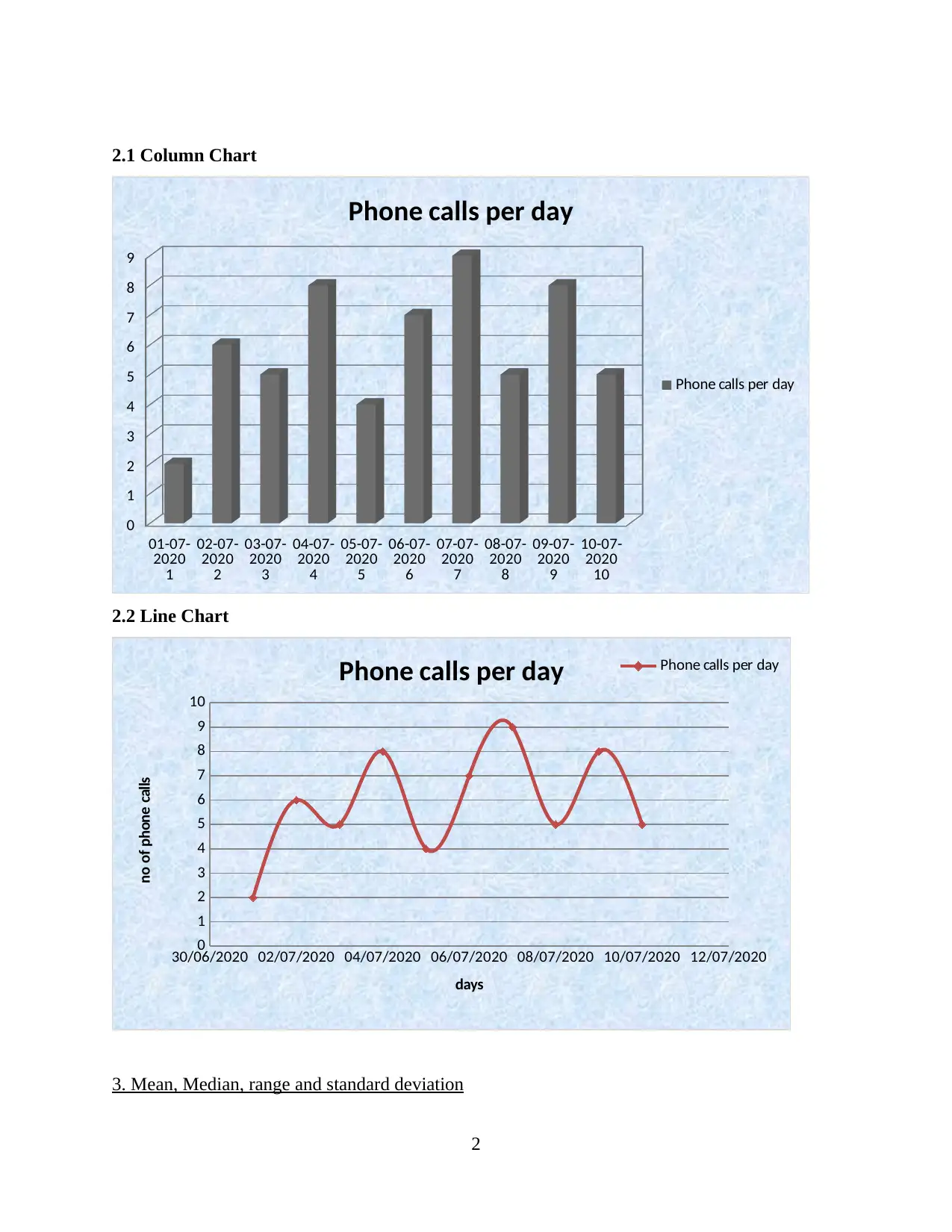
2.1 Column Chart
01-07-
2020 02-07-
2020 03-07-
2020 04-07-
2020 05-07-
2020 06-07-
2020 07-07-
2020 08-07-
2020 09-07-
2020 10-07-
2020
1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
Phone calls per day
Phone calls per day
2.2 Line Chart
30/06/2020 02/07/2020 04/07/2020 06/07/2020 08/07/2020 10/07/2020 12/07/2020
0
1
2
3
4
5
6
7
8
9
10
Phone calls per day Phone calls per day
days
no of phone calls
3. Mean, Median, range and standard deviation
2

3.1 The mean
Mean is significantly used to find the average value associated with the specific data sets in
statistics. It helps in analysing and make appropriate decision (SEPTIO A, 2015).
Sr. No. Date
Phone calls
per day
1 01-07-2020 2
2 02-07-2020 6
3 03-07-2020 5
4 04-07-2020 8
5 05-07-2020 4
6 06-07-2020 7
7 07-07-2020 9
8 08-07-2020 5
9 09-07-2020 8
10 10-07-2020 5
Sum total of phone
calls 59
No. of observation 10
Mean 5.9
Within the above data mean is calculated by the sum of observation which is further
divided by the number of data observed. It helps in examining the average happening of the
value within the given set of data. Mean in the data for phone calls is 5.9.
3.2 The Median
This is referred to as a simple measure associated with the central tendency. It helps in arranging
the observations within the specific order. In case of odd number of observation the median is
considered to be as the median value. In case of even number the median is considered to be as
the average of the 2 values of observation.
Sr. No. Date
Data in
relation to
phone calls
per day
1 01-07-2020 2
2 02-07-2020 6
3 03-07-2020 5
4 04-07-2020 8
5 05-07-2020 4
3

6 06-07-2020 7
7 07-07-2020 9
8 08-07-2020 5
9 09-07-2020 8
10 10-07-2020 5
No. of
observation 59
M= (10+1)/2 5.5
M= (4+7)/2 5.5
Median for phone calls in a day is computed by averaging the mid- values which are
values of the day 5th and 6th that are 4 and 7 respectively. Upon averaging these two values the
mid value is calculated as 5.5.
3.3 The Mode
It is considered to be as the specific set of value which tends to occur the most number of times
within the specific data set (Nowakowski, 2020).
Date
Phone calls per
day
01-07-2020 2
02-07-2020 6
03-07-2020 5
04-07-2020 8
05-07-2020 4
06-07-2020 7
07-07-2020 9
08-07-2020 5
09-07-2020 8
10-07-2020 5
Mode = 5
The mode of the specific data sets is 5 which tends to shows that, in the duration of 10 days the
specific user has received 5 calls 3 times a day.
3.4 The Range
Range within statistics is considered to be as a method which helps in examining the
variance between the minimum value and maximum value within the data sets.
4

Particulars Formula Amount
Maximum 9
Minimum 2
Range
Largest value-Smallest
value 7
Range of the specific call is considered to be 7 because the highest value is amounted to
be 9 and moreover the lowest value is amounted to be 2. However, the difference between the
two values is 7.
3.5 The standard deviation
It helps in examining the variance of the specific outcomes associated with the mean value
(Peleg, 2019).
Date Phone calls (X) X^2
01-07-2020 2 4
02-07-2020 6 36
03-07-2020 5 25
04-07-2020 8 64
05-07-2020 4 16
06-07-2020 7 49
07-07-2020 9 81
08-07-2020 5 25
09-07-2020 8 64
10-07-2020 5 25
Total 59 389
Standard deviation= Square root of ∑x^2 / N – (∑x / n) ^ 2
SQRT of (389 / 59) – (59 / 10) ^ 2
SQRT of 6.59 – 34.81
SQRT of -28.22
5.31
Standard deviation of this given observation is estimated to be 5.31 which in turn is not
considered to be very high. However, the spreading from the value of mean is less.
4 Linear Forecasting
Date X
Phone calls
(Y) X*Y X^2
01-07-2020 1 2 2 1
02-07-2020 2 6 12 4
03-07-2020 3 5 15 9
5

04-07-2020 4 8 32 16
05-07-2020 5 4 20 25
06-07-2020 6 7 42 36
07-07-2020 7 9 63 49
08-07-2020 8 5 40 64
09-07-2020 9 8 72 81
10-07-2020 10 5 50 100
Total 55 59 348 385
4.1 “m” value
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
m = 10 (348) - (55 * 59) / (10 * 385) – (55)^2
m = (3480 – 3245) / (3850 – 3025)
m = 235/ 825
m = 0.28
4.2 “c” value
c = Σy – m Σx / N
c = 59 – (0.28 * 55) / 10
c = (59 – 15.4) / 10
c = 43.6 / 10
c = 4.36
4.3 Day 12 Forecasting
Y = mX + c
= 0.28 * (12) + (4.36)
= 3.36 + 4.73
= 8.09 = 8 calls approx
4.4 Day 14 Forecasting
Y = mX + c
= 0.28 * (14) + (4.36)
= 3.92 + 4.36
= 8.28 = 8 calls approx
6

It could be analysed that using the linear forecasting, forecast for calls on 12th and 14th
day is 8. The analysis is used by the researchers for making forecast of the future outcomes. This
is an effective method used in statistics for drawing results and framing accurate conclusions.
CONCLUSION
It could be concluded from the above study about descriptive data analysis that it plays an
important role in analysis of the data. Report has increased the practical understanding about the
use of different method in statistics.
7

REFERENCES
Books and Journals
Nowakowski, S., 2020. Uniqueness of a Median of a Binomial Distribution with Rational
Probability. arXiv preprint arXiv:2004.03280.
Peleg, M., 2019. Beta distributions for particle size having a finite range and predetermined
mode, mean or median. Powder Technology, 356, pp.790-794.
SEPTIO A, A.L.B.E.R.T.U.S., 2015. Statistical Calculation of Mean, Median, Mode, and
Standard Deviation Using PHP programming language (Doctoral dissertation, Prodi Teknik
Informatika Unika Soegijapranata).
8