Data Analysis and Forecasting

This report provides an understanding of data analysis and forecasting techniques. It covers tabular and graphical representation, descriptive analysis, and a linear forecasting model. The report also discusses the process of predicting future values based on present data.

Data Analysis and
Forecasting

Contents
INTRODUCTION...........................................................................................................................1
MAIN BODY..................................................................................................................................1
Tabular data representation..........................................................................................................1
Graphical data representation......................................................................................................1
Computing and discussing descriptive analysis..........................................................................2
Linear forecasting model.............................................................................................................4
CONCLUSION................................................................................................................................6
REFERENCES................................................................................................................................7

INTRODUCTION
Data forecasting is a process of predicting future data values by analysing present values.
This process involves scaling and transformation of data as well (Wang, Wang and Zhang,
2018). The main aim of developing this report is to develop an understanding about data analysis
for which the data for phone calls made in each days for 10 consecutive days is collected which
is then analysed using various techniques involving tabular and graphical representation along
with descriptive analysis and forecast analysis.
MAIN BODY
Tabular data representation
The collected data is represented below using a vertical table having 2 columns and 11
rows.
Date Phone calls made each day
10-Aug-20 15
11-Aug-20 17
12-Aug-20 20
13-Aug-20 25
14-Aug-20 22
15-Aug-20 26
16-Aug-20 28
17-Aug-20 29
18-Aug-20 21
19-Aug-20 30
Graphical data representation
The collected data is now represented using two types of graphs which are bar graph and
area chart. These charts are developed by using a software application of Microsoft Excel.
Bar graph:
1

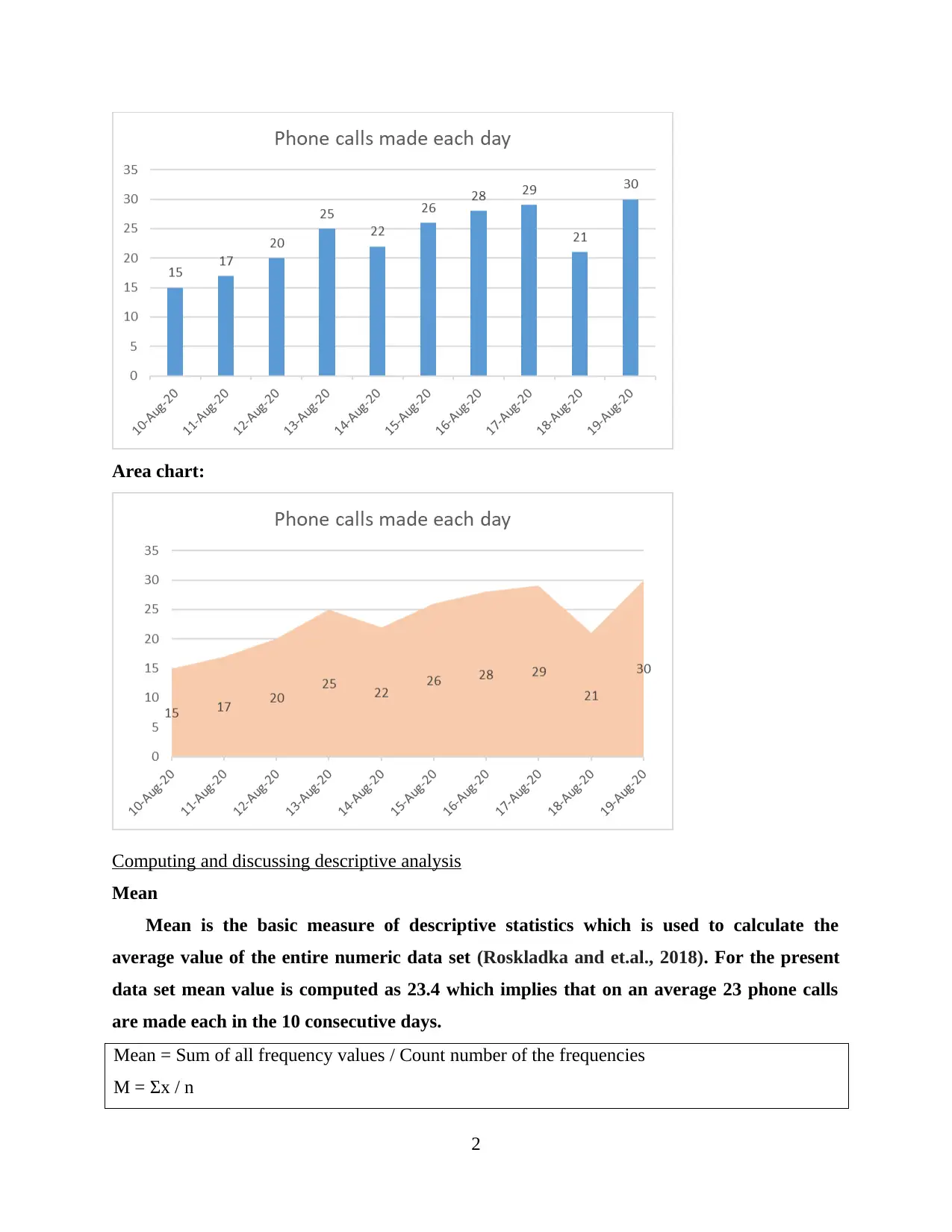
Area chart:
Computing and discussing descriptive analysis
Mean
Mean is the basic measure of descriptive statistics which is used to calculate the
average value of the entire numeric data set (Roskladka and et.al., 2018). For the present
data set mean value is computed as 23.4 which implies that on an average 23 phone calls
are made each in the 10 consecutive days.
Mean = Sum of all frequency values / Count number of the frequencies
M = Σx / n
2

= 234 / 10
= 23.4
Mean is 23.4
Median
Median is a statistical metric which provides the middle value of the entire data set. It is the
midpoint of the entire dataset which divides the dataset into two equal sections. The mid value of
phone call data is 23.5
Formula of Median = (Count of frequencies + 1) / 2
= (10 + 1) / 2
= 5.5
5th frequency = 22
6th frequency = 26
5.5th position = Median = 23.5
Mode
This measure is most significant element of descriptive statistics which helps in returning
the most recurring value of the data set. This element is used highly to determine most common
value of the dataset (Sengupta and Mugde, 2020). By looking at the phone call data, it is clear
that mode is 22 as this value is repeated two times.
Range
This measure is the difference between maximum and minimum value of the data set. Range
of the present data set is 15.
Range = Maximum frequency value – Minimum frequency value
= 30 – 15
= 15
Range of this dataset is 15
Standard Deviation
The metric of standard deviation helps in calculating the dispersion in a dataset which all
values have to its mean. A large standard deviation indicates larger dispersion and vice versa.
The standard deviation of the present dataset is calculated by computing the square root of
variance which is 4.84.
Standard Deviations =√ (variance)
3

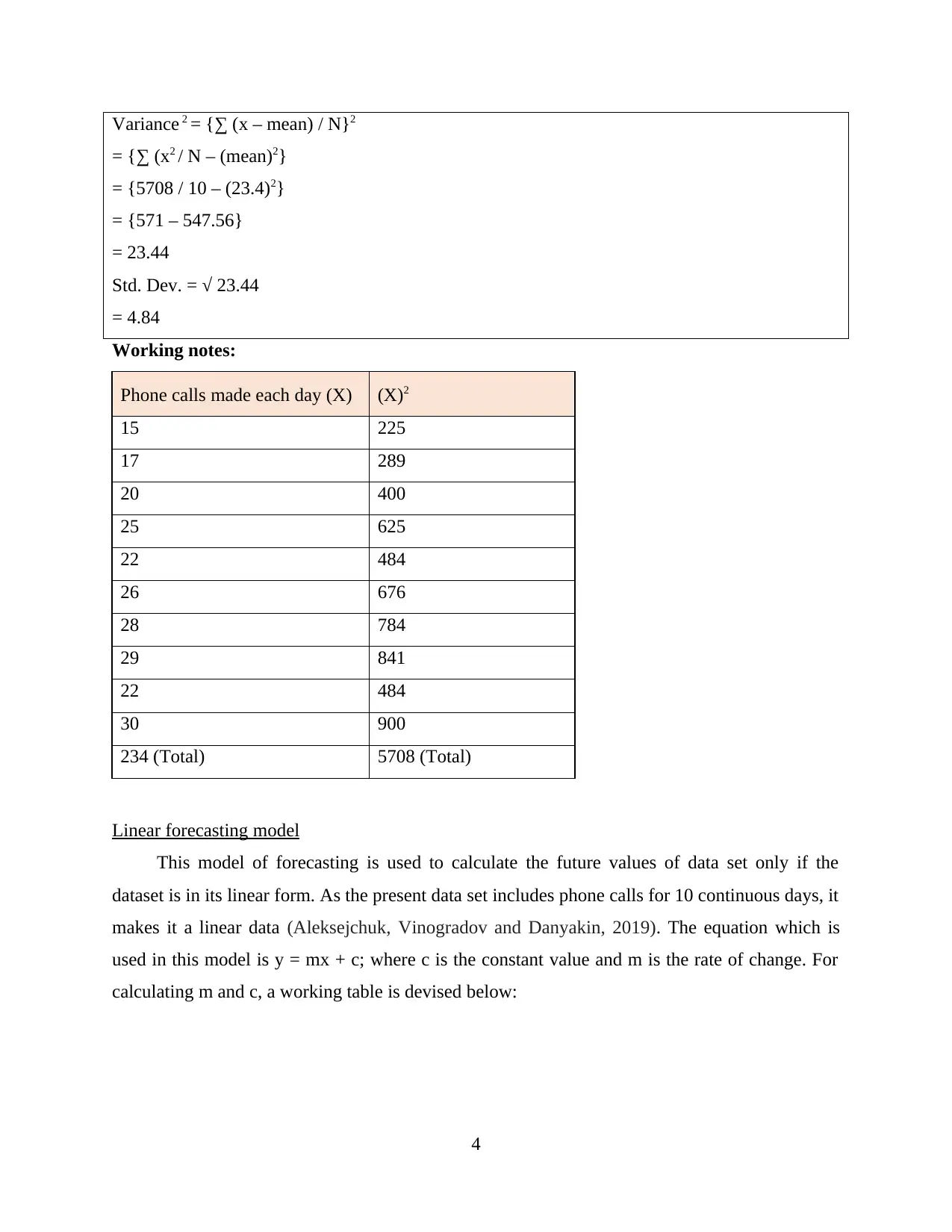
Variance 2 = {∑ (x – mean) / N}2
= {∑ (x2 / N – (mean)2}
= {5708 / 10 – (23.4)2}
= {571 – 547.56}
= 23.44
Std. Dev. = √ 23.44
= 4.84
Working notes:
Phone calls made each day (X) (X)2
15 225
17 289
20 400
25 625
22 484
26 676
28 784
29 841
22 484
30 900
234 (Total) 5708 (Total)
Linear forecasting model
This model of forecasting is used to calculate the future values of data set only if the
dataset is in its linear form. As the present data set includes phone calls for 10 continuous days, it
makes it a linear data (Aleksejchuk, Vinogradov and Danyakin, 2019). The equation which is
used in this model is y = mx + c; where c is the constant value and m is the rate of change. For
calculating m and c, a working table is devised below:
4

Date Day (X)
Phone calls
made each
day (Y)
XY X^2
10-Aug-20 1 15 15 1
11-Aug-20 2 17 34 4
12-Aug-20 3 20 60 9
13-Aug-20 4 25 100 16
14-Aug-20 5 22 110 25
15-Aug-20 6 26 156 36
16-Aug-20 7 28 196 49
17-Aug-20 8 29 232 64
18-Aug-20 9 22 198 81
19-Aug-20 10 30 300 100
Total 55 234 1401 385
Calculation of m value
Particulars Details
m NΣxy – Σx Σy / NΣ x ^ 2 – (Σx) ^ 2
(10 * 1401) - (55 * 234) / (10 * 385) -
(55) ^ 2
(14010 - 12870) / (3850 - 3025)
1140 / 825
1.38
Calculation of c value
Particulars Details
c Σy - m Σx / N
(234 - (1.38 * 55)) / 10
15.81
5

Forecasting the number of calls making on day 12 and day 14
Forecast of 12th day
y = mx + c
y 1.38 (x) + 15.81
x 12
y 1.38 (12) + 15.81
32.37
Forecast of 14th day
y = mx + c
y 1.38 (x) + 15.81
x 14
y 1.38 (14) + 15.81
35.13
Using the values calculated for m and c, the value of y is calculated when the x was 12
and 14. Using the linear forecasting model, it has been ascertained that if the value of “x” is 12
or 12th day, then the estimated number of phone calls will be 32 and when “x” is 14th day, it is
estimated that the count of phone calls will be 35. These predictions are made by considering the
constant as 15.81 and the rate of change as 1.38. These values which are computed for day 12th
and 14th are only the estimated values and real ones can be different from these as this model
does not account for any external factors which can impact the constant and rate of change
(Zgurovsky and Zaychenko, 2016).
CONCLUSION
The above report is a summarisation of data analysis of a data set of regular phone calls.
This summarisation has helped in reaching to a conclusion that a continuous data set can be used
to predict future values by using linear forecasting model. It has been also concluded that
descriptive statistics metric can help in analysing the data.
6

REFERENCES
Books and Journals
Aleksejchuk, A.S., Vinogradov, V.I. and Danyakin, K.D., 2019. The Tasks of Analysis and
Forecasting the Activities of IT Companies Using Machine Learning Methods. Modelling
and Data Analysis. 9(4). pp.57-66.
Roskladka, A. and et.al., 2018. Data analysis and forecasting of tourism development in
Ukraine. Innovative Marketing. 14(4). pp.19-33.
Sengupta, S. and Mugde, S., 2020. Covid-19 Pandemic Data Analysis and Forecasting using
Machine Learning Algorithms. medRxiv.
Wang, J., Wang, C. and Zhang, W., 2018. Data analysis and forecasting of tuberculosis
prevalence rates for smart healthcare based on a novel combination model. Applied
Sciences. 8(9). p.1693.
Zgurovsky, M.Z. and Zaychenko, Y.P., 2016. Inductive modeling method (GMDH) in problems
of intellectual data analysis and forecasting. In The Fundamentals of Computational
Intelligence: System Approach (pp. 221-260). Springer, Cham.
7