Numeracy and Data Analysis Report

This report analyzes data on passenger usage at Dorchester West station in London over a ten-year period. It includes calculations of mean, mode, median, range, and standard deviation, as well as the presentation of data in charts. The report also explores the calculation of station usage indicators using a linear regression model. This report is available on Desklib, a website that provides past papers and solved assignments for students.

Numeracy and Data
Analysis

Table of Contents
INTRODUCTION...........................................................................................................................1
MAIN BODY...................................................................................................................................1
1. Data in table format.................................................................................................................1
2. Presentation of data in charts...................................................................................................1
3. Calculation of mean, mode, median, range, Standard deviation.............................................2
4. Calculation of m, c and station usage indicator.......................................................................5
CONCLUSION................................................................................................................................6
REFERENCES................................................................................................................................7

INTRODUCTION
Data analysis is a procedure which is used by researchers to analyse and transform the
information which is gathered for specific purpose. With the help of it results for different
procedures can be analysed. There are various types of techniques that are used for the purpose
of analysing data and determining results. This report is based upon calculation of different
topics such as mean, mode, median, standard deviation, range and other factors which are based
upon weather of
MAIN BODY
1. Data in table format
The data is gathered for Dorchester West station for ten years (Train station usage in
London, 2019). It is represented in the form of table which is as follows:
Year
Number of
passengers
2009 133
2010 44
2011 123
2012 58
2013 11
2014 10
2015 12
2016 37
2017 80
2018 39
2. Presentation of data in charts
Column chart:
1

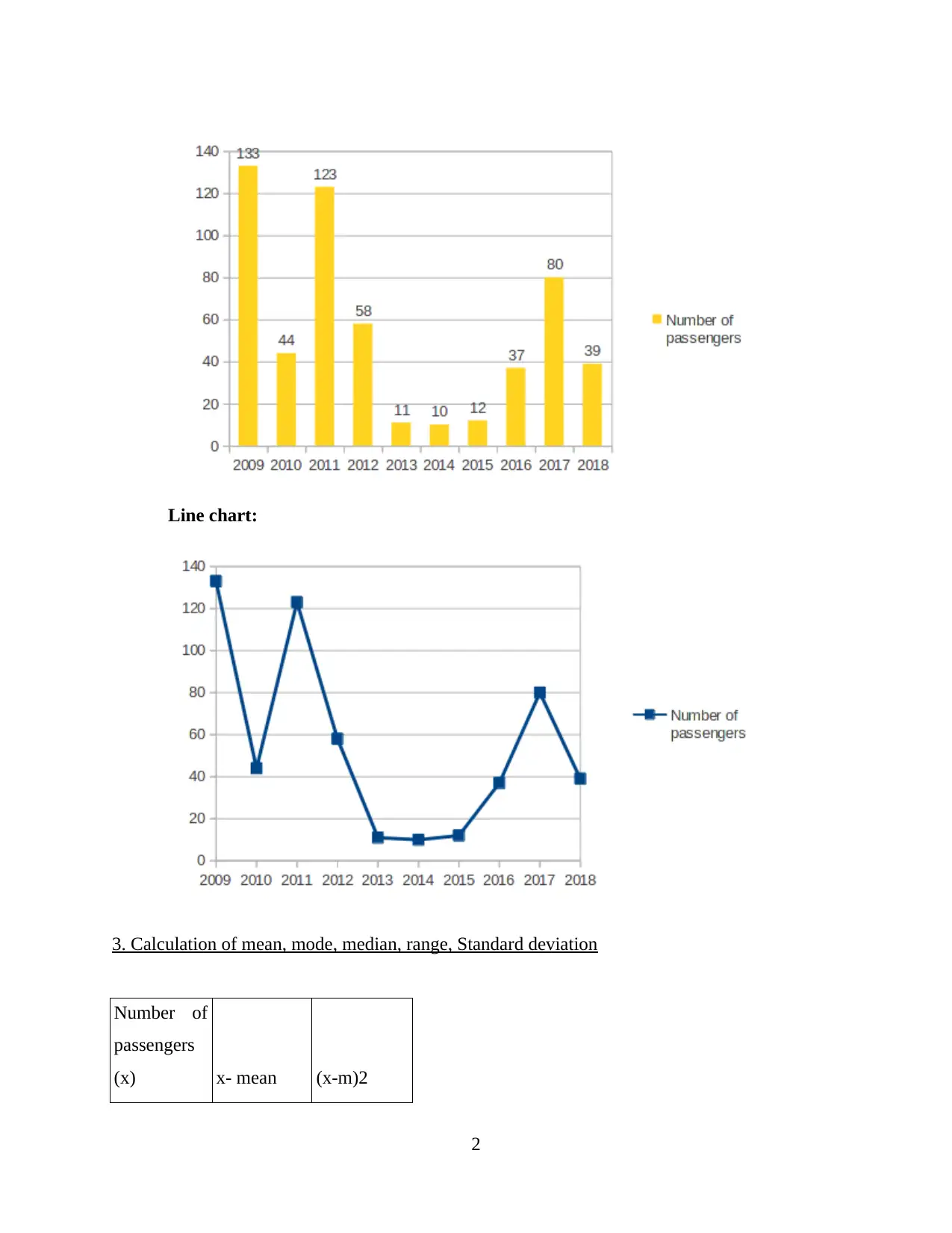
Line chart:
3. Calculation of mean, mode, median, range, Standard deviation
Number of
passengers
(x) x- mean (x-m)2
2

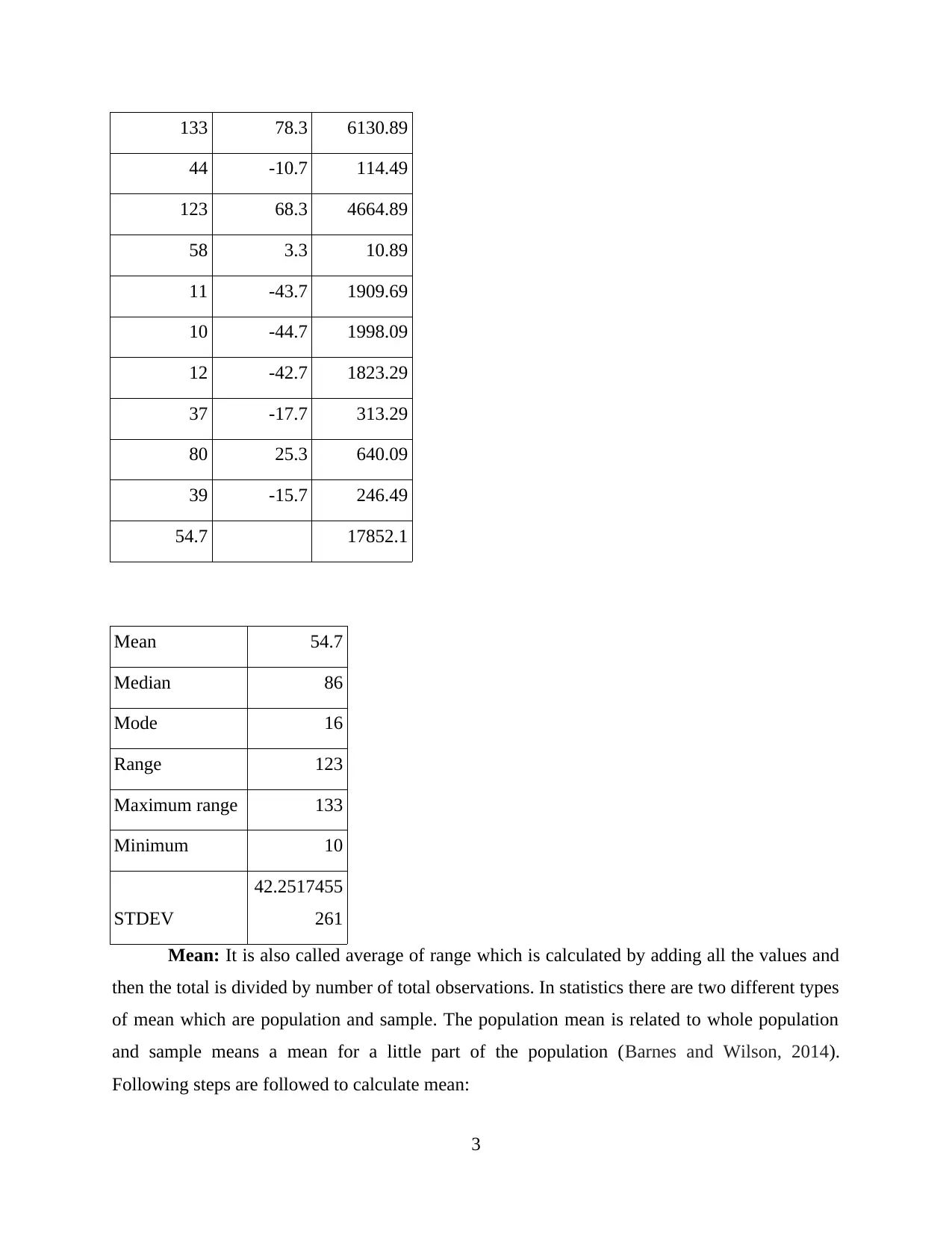
133 78.3 6130.89
44 -10.7 114.49
123 68.3 4664.89
58 3.3 10.89
11 -43.7 1909.69
10 -44.7 1998.09
12 -42.7 1823.29
37 -17.7 313.29
80 25.3 640.09
39 -15.7 246.49
54.7 17852.1
Mean 54.7
Median 86
Mode 16
Range 123
Maximum range 133
Minimum 10
STDEV
42.2517455
261
Mean: It is also called average of range which is calculated by adding all the values and
then the total is divided by number of total observations. In statistics there are two different types
of mean which are population and sample. The population mean is related to whole population
and sample means a mean for a little part of the population (Barnes and Wilson, 2014).
Following steps are followed to calculate mean:
3

 First of total of all the values is calculated.
 In second and last step the total is divided by number of observations
Formula: ∑X/ N
∑X= Total of values
N= Number of observations
In current situation mean is 54.7.
Mode: A number which appears maximum times in the values is known as mode. In
other words it can be defined as the value which is sampled most often. If there is no number
which is being repeated in the list then it shows that there is no mode in whole calculation.
Following steps are followed to calculate it:
 First of all data is collected in ascending order in order to make separation of such
number which are repeating.
 Afterwards one number is selected which is being repeating maximum times.
Mode for this case is 16.
Median: It can be defined as the middle number which separates the lower and upper
half of the values which are gathered for the purpose of analysing results. If the data series is in
odd observations then the one middle number will be considered as median and in case of odd
number of observations middle two numbers are considered as median for whole group. Steps
that are followed to calculate it are as follows:
 At first stage data is added in to series of lowest to highest.
 If observation is odd then middle number will be median.
 If observation is even then two middle numbers will be the median (Chen and Feeley,
2014).
Formula: (N+1)/ 2
Median for above calculations is 86.
Range: It can be defined as the difference between highest and lowest limit of the values.
In order to find range first of all data is segregated in the format of lower to higher. Afterwards
smaller value is deducted from the larger number of the data series (Estrada-Mejia, de Vries and
Zeelenberg, 2016). Steps to calculate it are as follows:
 Identify the highest and lowest values from data series.
 Afterwards subtract lower one from the larger one.
4

Formula: MAX- MIN
In the above calculation the range is 123 (133-10)
Standard deviation: It is mainly calculated for the purpose of determining or measuring
the variation within the value of a specific data series. The sign which is used to denote it is σ. It
is root of variance of all the values. Steps that are uised to calculate it are as follows:
 First of all data is required to be arranges in to continuous series.
 In second step formula is applied which is based upon the nature of series.
 At the end standard deviation is calculated with the help of the formula.
Formula:
In above calculations standard deviation is 42.25.
4. Calculation of m, c and station usage indicator
In order to get value of y, m and c are estimated. Value of m is 5 and value of c is 15. The
calculation of y is as follows which is based upon a formula which is y= mx+c.
Year
Number of
passengers
(x) Y (mx+c)
2009 133 680
2010 44 235
2011 123 630
2012 58 305
2013 11 70
2014 10 65
2015 12 75
2016 37 200
2017 80 415
2018 39 210
5

1. Calculation of m = change in y/ change in x
2. Calculation of c: It remain constant so it is calculated by following formula:
c=y-mx
Using the values above calculation of m and c station indicators are calculated for year 12
and 15 which are 401 and 401.6 respectively (Mulligan, 2015).
It is calculated in excel and the formula which is used for calculation is
FORECAST(Value;data_x;data_y).
CONCLUSION
From the above project report it has been concluded data analysis is a process which is
used for the purpose of transforming and analysing information which is collected for the
purpose of finding appropriate results for different problems. In order to get correct and
appropriate results it is vital to use appropriate methods which assures accuracy of the result.
6

REFERENCES
Books and Journals:
Barnes, T. J. and Wilson, M. W., 2014. Big data, social physics, and spatial analysis: The early
years. Big Data & Society. 1(1). p.2053951714535365.
Chen, Y. and Feeley, T. H., 2014. Numeracy, information seeking, and self-efficacy in managing
health: an analysis using the 2007 Health Information National Trends Survey
(HINTS). Health communication. 29(9). pp.843-853.
Estrada-Mejia, C., de Vries, M. and Zeelenberg, M., 2016. Numeracy and wealth. Journal of
Economic Psychology. 54. pp.53-63.
Mulligan, J., 2015. Moving beyond basic numeracy: data modeling in the early years of
schooling. ZDM. 47(4). pp.653-663.
Online
Train station usage in London. 2019. [Online]. Available through:
<https://data.london.gov.uk/dataset/train-station-usage>
7