(Solution) Data Analysis : Assignment

Numeracy and Data Analysis

Table of Contents
INTRODUCTION................................................................................................................................3
MAIN BODY.......................................................................................................................................3
1. Arrangement of data set in table form.........................................................................................3
2. Presentation of data in form of line chart and column chart. ......................................................3
3. Calculating and defining steps of following statistical tools.......................................................5
4. Linear forecasting model y = mx + c...........................................................................................7
(i) Steps for calculating m value .....................................................................................................7
(ii) Defining steps to assess value of c.............................................................................................8
(iii). Forecasting of wind speed for 14 and 21 days.........................................................................8
CONCLUSION....................................................................................................................................9
REFERENCES...................................................................................................................................10

INTRODUCTION
Data analysis is related with process of making proper and better interpretation of given data set
with the help of appropriate statistical tools. By making correct analysis of data collected it assists
in making crucial decision as well. The present report is based on study of wind speed for past ten
consecutive days of Stratford city, United kingdom. With the help of tables and graphs data will be
analysed for better understanding.
MAIN BODY
1. Arrangement of data set in table form.
Days Date Wind speed km/h
1 14/09/19 4.32
2 15/09/19 12.07
3 16/09/19 5.82
4 17/09/19 14.34
5 18/09/19 5.9
6 19/09/19 6.95
7 20/09/19 16.74
8 21/09/19 10.97
9 22/09/19 12.39
10 23/09/19 20.06
2. Presentation of data in form of line chart and column chart.
Line Chart – Also known as line graph which helps in displaying data set and information
about a particular phenomenon with the help of lines (Dickie, Feldman and Meyers, 2017). This
graph makes use of lines so as to establish connection in between different data points depicting
about different quantitative figures of a particular time period.

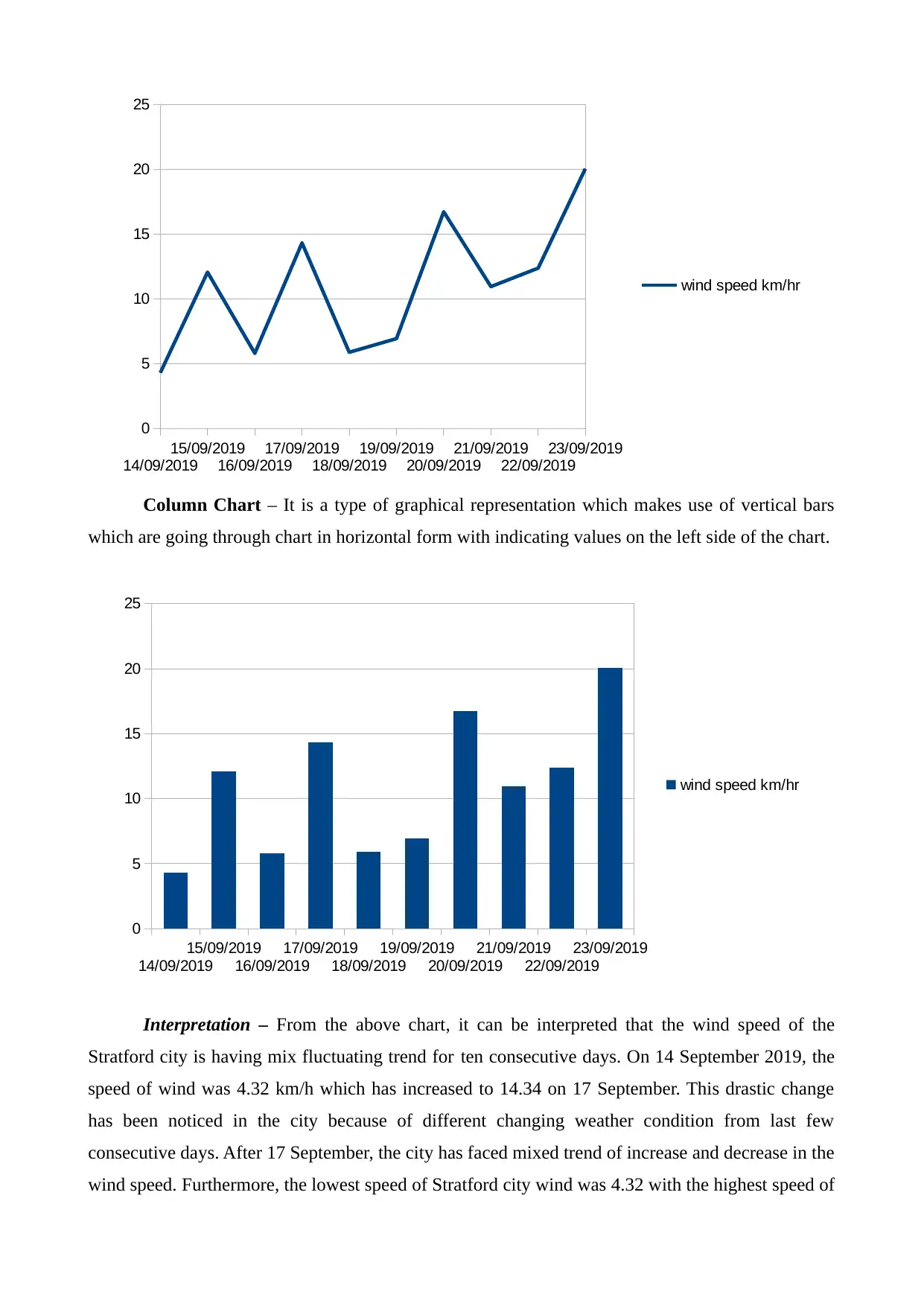
Column Chart – It is a type of graphical representation which makes use of vertical bars
which are going through chart in horizontal form with indicating values on the left side of the chart.
Interpretation – From the above chart, it can be interpreted that the wind speed of the
Stratford city is having mix fluctuating trend for ten consecutive days. On 14 September 2019, the
speed of wind was 4.32 km/h which has increased to 14.34 on 17 September. This drastic change
has been noticed in the city because of different changing weather condition from last few
consecutive days. After 17 September, the city has faced mixed trend of increase and decrease in the
wind speed. Furthermore, the lowest speed of Stratford city wind was 4.32 with the highest speed of
14/09/2019
15/09/2019
16/09/2019
17/09/2019
18/09/2019
19/09/2019
20/09/2019
21/09/2019
22/09/2019
23/09/2019
0
5
10
15
20
25
wind speed km/hr
14/09/2019
15/09/2019
16/09/2019
17/09/2019
18/09/2019
19/09/2019
20/09/2019
21/09/2019
22/09/2019
23/09/2019
0
5
10
15
20
25
wind speed km/hr

20.06 on September 23.
3. Calculating and defining steps of following statistical tools.
Particulars Wind speed (in
km/h)
Mean 10.956
Median 11.52
Mode #NA
Range 15.74
Standard
Deviation 5.197
Steps for calculating:
1. Mean – For determining the average value of a given data set, all the numbers as given in
the data set are needed to be arrange together. These numbers can be small or big in value.
After arranging all the values the next step is related with summation of it. All the numbers
should be added together to find a sum which later on will be divided by the total number of
values present in the data set (Floater and Patrizi, 2019). After dividing the total summed up
value with the total number of counts of data set, the value obtained will be called as Mean
value.
Date Wind Speed
km/h
14/09/19 4.32
15/09/19 12.07
16/09/19 5.82
17/09/19 14.34
18/09/19 5.9
19/09/19 6.95
20/09/19 16.74
21/09/19 10.97
22/09/19 12.39
23/09/19 20.06
N = 10
Total (∑X) 109.56
Mean
∑X ÷ N
109.56 / 10
= 10.956
2. Median – All the numbers given in set is required to be arranged from lowest to the highest
order. After sorting of data, one should identify whether the number of items in given data
set is of even or odd number. In case of even number, median will be found out by taking

mean of two middle numbers. Whereas in case of odd number, the number present in the
middle of given list will be considered as median.
Date Wind Speed km/h
14/09/19 4.32
15/09/19 5.82
16/09/19 5.9
17/09/19 6.95
18/09/19 10.97
19/09/19 12.07
20/09/19 12.39
21/09/19 14.34
22/09/19 16.74
23/09/19 20.06
Median
(N + 1) / 2
= (10 + 1)/2
= 11 / 2
= 5.5 item
Median
(Value of 5th item +
value of 6th item) /
2 = (10.97 +12.07) /
2 = 11.52
3. Mode – Write down all numbers in increasing order ranging from lowest to highest. Count
the number of times each number is coming (Maxwell, Delaney and Kelley, 2017). Most
often repeating number will be considered as mode value of that set.
Particulars Wind speed (in
km/h)
Mode #NA
4. Range – For ascertaining range value, one is required to first determine minimum and
maximum value of the particular data set of which range is to be identified. After evaluating
highest and lowest value, range can be determined by subtracting the smallest value from
the largest one present in set.
Particulars Figures
Maximum wind
speed 20.06
Minimum wind
speed 4.32
Range 15.74

= Maximum –
Minimum value
5. Standard Deviation – In case of standard deviation calculation, mean value is determined
first. After that for each value, mean is subtracted and result obtained is squared. For such
difference value obtained thereafter again mean value is required to be obtained (Quan and
et.al., 2018). At last, by calculating square root of value obtained, standard deviation is
ascertained.
Date Wind Speed
km/h X^2
14/09/19 4.32 18.6624
15/09/19 12.07 145.6849
16/09/19 5.82 33.8724
17/09/19 14.34 205.6356
18/09/19 5.9 34.81
19/09/19 6.95 48.3025
20/09/19 16.74 280.2276
21/09/19 10.97 120.3409
22/09/19 12.39 153.5121
23/09/19 20.06 402.4036
Total 109.56 1443.452
Standard deviation= SQRT of ∑x^2 / N – (∑x / n) ^ 2
= SQRT of (1443.452 / 10) – (109.56 / 10) ^ 2
= SQRT of 144.3452– 120.034
= SQRT of = 24.311
= 5.197
4. Linear forecasting model y = mx + c
(i) Steps for calculating m value
With the help of following formula the value of m can be calculated:
m = N Σxy – Σx Σy / N Σ x^2 – (Σx)^2
Step 1. The total number of observation is multiplied by Σxy
Step 2. Value of Σx is multiplied by Σy
Step 3. Number of observation is multiplied by sum of X square
Step 4. Square of Σx value needs to calculated
Step 5. Result of 2 is deducted from 1.

Step 6. Step 4 - 3
Step 7. Step 5 - 6
(ii) Defining steps to assess value of c
c = Σy - mΣx / N
Step 1. Sum of y value is calculated.
Step 2. Σx is determined which is multiplied with m value obtained.
Step 3. Value obtained in step 2 is divided by the total number of observations present.
Step 4. At last value derived in step 3 is subtracted from Σy.
(iii). Forecasting of wind speed for 14 and 21 days.
Date Number of
days (X)
Total wind
speed (Y) XY X^2
14/09/19 1 4.32 4.32 1
15/09/19 2 12.07 24.14 4
16/09/19 3 5.82 17.46 9
17/09/19 4 14.34 57.36 16
18/09/19 5 5.9 29.5 25
19/09/19 6 6.95 41.7 36
20/09/19 7 16.74 117.18 49
21/09/19 8 10.97 87.76 64
22/09/19 9 12.39 111.51 81
23/09/19 10 20.06 200.6 100
Total 55 109.56 691.53 385
Particulars Formula Y = mX + c
m NΣxy – Σx Σy / NΣ x^2 – (Σx)^2 M = 10 (691.53) - (55 * 109.56) / (10
* 385) – (55)^2
m = (6915.3 – 6025.8) / (3850 –
3025)
m = 889.5 / 825
m = 1.078

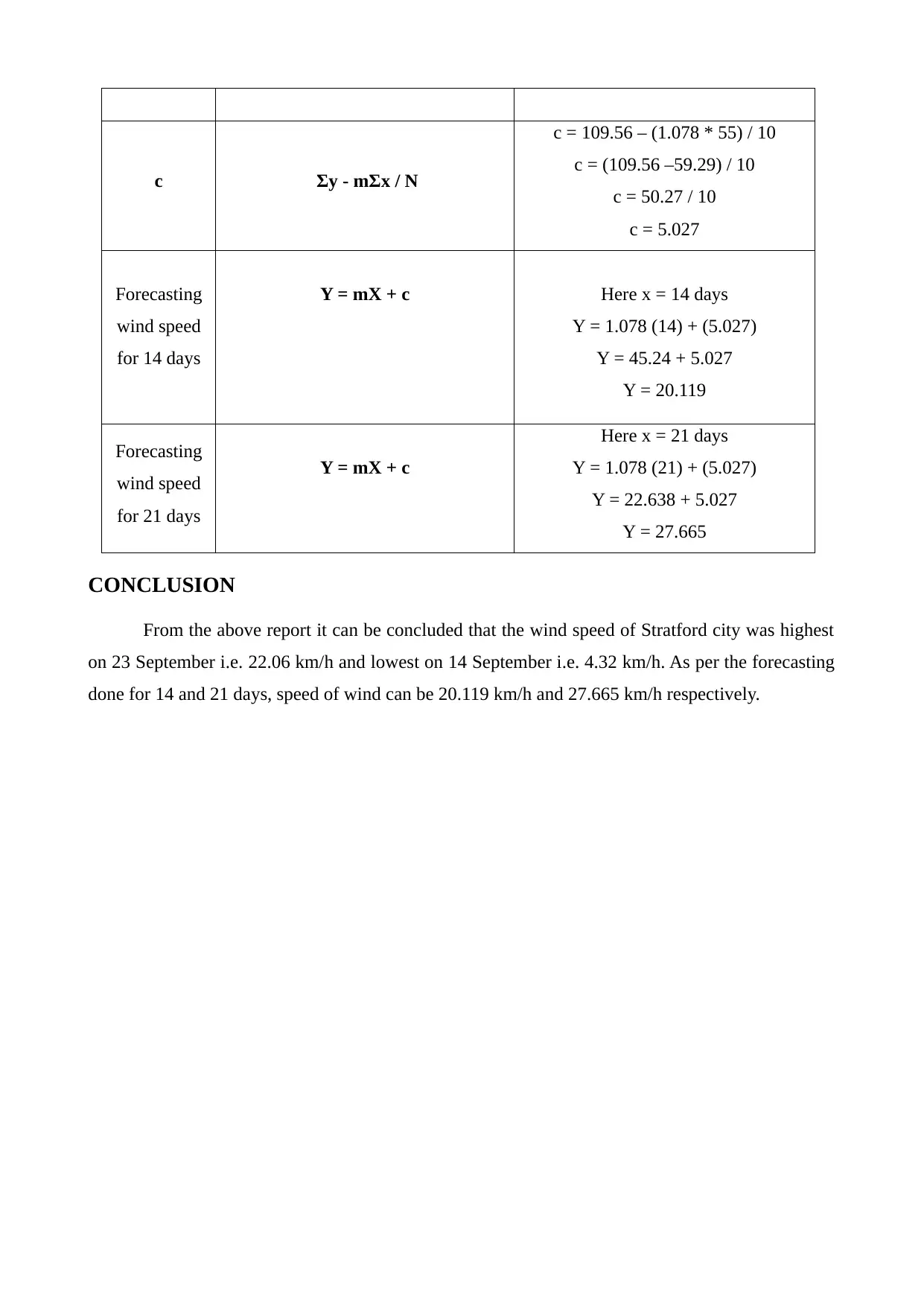
c Σy - mΣx / N
c = 109.56 – (1.078 * 55) / 10
c = (109.56 –59.29) / 10
c = 50.27 / 10
c = 5.027
Forecasting
wind speed
for 14 days
Y = mX + c Here x = 14 days
Y = 1.078 (14) + (5.027)
Y = 45.24 + 5.027
Y = 20.119
Forecasting
wind speed
for 21 days
Y = mX + c
Here x = 21 days
Y = 1.078 (21) + (5.027)
Y = 22.638 + 5.027
Y = 27.665
CONCLUSION
From the above report it can be concluded that the wind speed of Stratford city was highest
on 23 September i.e. 22.06 km/h and lowest on 14 September i.e. 4.32 km/h. As per the forecasting
done for 14 and 21 days, speed of wind can be 20.119 km/h and 27.665 km/h respectively.

REFERENCES
Books and Journals
Dickie, G. A., Feldman, D. J. and Meyers, D. L., International Business Machines Corp,
2017. Merging metadata for database storage regions based on overlapping range values. U.S.
Patent 9,582,512.
Floater, M. S. and Patrizi, F., 2019. Transfinite mean value interpolation over polygons. arXiv
preprint arXiv:1906.08358.
Lind, H. B. and et.al., 2015. The value-belief-norm theory, personal norms and sustainable travel
mode choice in urban areas. Journal of Environmental Psychology. 44. pp.119-125.
Maxwell, S. E., Delaney, H. D. and Kelley, K., 2017. Designing experiments and analyzing data: A
model comparison perspective. Routledge.
Quan, H. and et.al., 2018. Estimation of Standard Deviation for a Log-Transformed Variable Based
on Summary Statistics in the Original Scale. Statistics in Biopharmaceutical Research. 10(1).
pp.30-38.
Online
Median formula steps. 2019. [Online]. Available through:
<https://www.wallstreetmojo.com/median-formula/>.