Data Analysis and Forecasting: Phone Call Data Report

This report provides a comprehensive analysis of phone call data collected over ten consecutive days. It begins with an introduction to data analysis and its importance in various businesses. The main body of the report includes a detailed presentation of the data in tabular and chart formats, specifically line and column charts for effective visualization. Various statistical calculations are performed, including the determination of mean, median, mode, range, and standard deviation. The report then applies the linear forecasting method to predict the number of phone calls for future days. The conclusion summarizes the findings, emphasizing the significance of data analysis in decision-making. The report references relevant sources to support the analysis and methodologies employed.

Data Analysis &
Forecasting

Contents
INTRODUCTION.....................................................................................................................................3
MAIN BODY.............................................................................................................................................3
1.Entering data in table............................................................................................................................3
2. Presenting data in two types of chart...................................................................................................3
3. Calculation:.........................................................................................................................................4
4. Linear forecasting method...................................................................................................................9
CONCLUSION........................................................................................................................................11
REFERENCES........................................................................................................................................12

INTRODUCTION
In different kinds of businesses, there are numerous transactions are done which can be
financial and non-financial. Due to financial transactions, different data are collected for
analysis. In this aspect, data analysis technique plays a key role that is related to assessing all
types of financial data so that final outcome can be derived (Cole and Trinh, 2017). The report is
based on implementation of various data analysis techniques in regards to number of phone calls
made in ten consecutive days. In this report different statistical values are calculated like mean,
median, standard deviation etc. on the basis of data of phone calls. In the end of report
forecasting of number of phone calls for different days has been in accordance of linear
programming method.
MAIN BODY
1. Entering data in table.
Number of day Phone calls
1 12
2 15
3 17
4 20
5 25
6 12
7 18
8 20
9 12
10 27
2. Presenting data in two types of chart.
There are a range of charts and graphs which are used for presenting data. These charts
make data visualization more effective and attractive. The above mentioned data of
phone calls are presented in form of such charts:

Line chart- It is a kind of chart in which data are shown in a zig zag line. This line raise
and fall in accordance of nature of data.
1 2 3 4 5 6 7 8 9 10
0
5
10
15
20
25
30
12
15 17
20
25
12
18 20
12
27
Phone calls
Column Chart-This is defined as a form of chart under which data are presented in
vertical columns or pillars (Dimitriadis, Patton and Schmidt, 2019). Similar to above
chart, height of these columns depends on nature of data set.
Phone calls
0
5
10
15
20
25
30
12
15 17
20
25
12
18 20
12
27
PHONE CALLS
1 2 3 4 5 6 7 8 9 10
3. Calculation:
Mean- This is defined as a term of statistics which is computed with an aim of finding
middle value of data set. Below steps for calculating mean of above phone calls data are
mentioned in such manner:

Mean (μ): Sum of total values/number of values
Step one: Calculation of sum of values-
Number of day Phone calls
1 12
2 15
3 17
4 20
5 25
6 12
7 18
8 20
9 12
10 27
Total 178
Step two: Calculation of number of values
From above data set, this can be find out that number of value is 10 as there is data of ten
consecutive days.
Step three: Entering values in formula
Mean (μ): 178/10
= 17.8
Median: In the statistics, median is a value that is separating the maximum half from
minimum half of a particular data set (Rayat, 2018). Below steps for calculating median
of above phone calls data are mentioned in such manner:

Median: (N/2th item+ N/2th item + 1)2
Step one: Arranging data set in ascending order
Number of day Phone calls
1 12
2 12
3 12
4 15
5 17
6 18
7 20
8 20
9 25
10 27
Step two: Finding values needed in formula.
N: 10
N/2: 10/2
= 5th item
Step three: Entering values in formula.
Median: (5th item+ 5th item + 1)/2
= (5th item+6th item)/2
= (17+18)/2
= 35/2
= 17.5

Mode: It can be understood as a form of value from a data set whose frequency is higher.
There is no particular formula for individual data series to find out mode. Below value of
mode is computed in such manner:
Number of day Phone calls
1 12
2 15
3 17
4 20
5 25
6 12
7 18
8 20
9 12
10 27
From above mentioned table, this can be stated that value 12 has higher frequency that is
3. Hence, mode will be 12.
Range: In the statistics, range is difference of maximum and minimum values (Black and
Masten, 2020). Below steps for calculating median of above phone calls data are
mentioned in such manner:
Range: Maximum Value-Minimum value
Step one: Finding maximum and minimum value
Number of day Phone calls
1 12
2 15
3 17
4 20

5 25
6 12
7 18
8 20
9 12
10 27
From above data set, this can be find out that:
Maximum value= 27
Minimum value= 12
Step two: Entering values in formula.
Range: 27-12
= 15
Standard deviation: It is defined as measurement of value of variation from a particular
set of data (Ali, Bhaskar and Sudheesh, 2019). Below steps for calculating standard
deviation of above phone calls data are mentioned in such manner:
Standard deviation= √ (variance)
Variance: [∑ (x – μ) 2 / N]
Step one: Calculating value of variance:
Numbe
r of day
Numbe
r of
phone
calls
made
(x- μ)
(x- μ)²
μ:17.8

(x)
1 12 -5.8 33.64
2 15 -2.8 7.84
3 17 -0.8 0.64
4 20 2.2 4.84
5 25 7.2 51.84
6 12 -5.8 33.64
7 18 0.2 0.04
8 20 2.2 4.84
9 12 -5.8 33.64
10 27 9.2 84.64
[∑ (x – μ) 2=
255.6
Variance: (255.6/10)
= 25.56
Step two: Entering value of variance in formula
Standard deviation= √25.56
= 5.05
4. Linear forecasting method.
Calculation of value of m:
m= n (∑x y) - (∑x) (∑y)/ n(∑x2) -( ∑x)2
Step one: Calculating values of formula

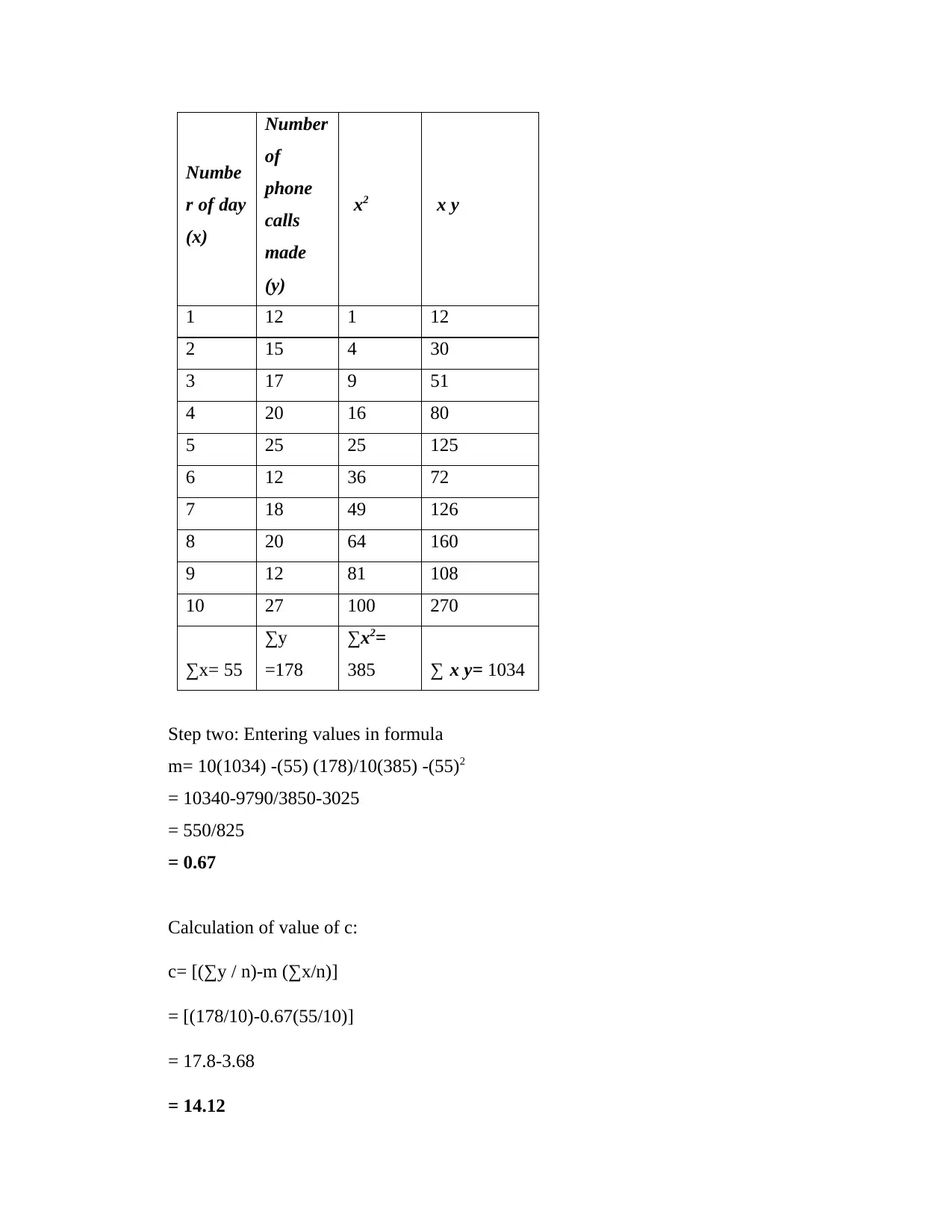
Numbe
r of day
(x)
Number
of
phone
calls
made
(y)
x2 x y
1 12 1 12
2 15 4 30
3 17 9 51
4 20 16 80
5 25 25 125
6 12 36 72
7 18 49 126
8 20 64 160
9 12 81 108
10 27 100 270
∑x= 55
∑y
=178
∑x2=
385 ∑ x y= 1034
Step two: Entering values in formula
m= 10(1034) -(55) (178)/10(385) -(55)2
= 10340-9790/3850-3025
= 550/825
= 0.67
Calculation of value of c:
c= [(∑y / n)-m (∑x/n)]
= [(178/10)-0.67(55/10)]
= 17.8-3.68
= 14.12

Forecasting for day 12 and 14:
Y: mx + c
Forecasting for day 12:
= 0.67*12+14.12
= 22.16 or 22 phone calls per day
Forecasting for day 14:
= 0.67*14+14.12
= 23.5 or 23 phone calls per day
CONCLUSION
On the basis of above report this can be concluded that data analysis is one of the crucial
technique that plays a key role for taking suitable decisions. In this project report, various kinds
of calculation of mean, mode, median has been done in order to find out relation among data of
phone calls. In the end part of report forecasting for day 12 and 14 has been done for estimated
number of phone calls by help of linear forecasting model.

REFERENCES
Books and journal:
Cole, A.P. and Trinh, Q.D., 2017. Secondary data analysis: techniques for comparing
interventions and their limitations. Current opinion in urology, 27(4), pp.354-359.
Dimitriadis, T., Patton, A.J. and Schmidt, P., 2019. Testing Forecast Rationality for Measures of
Central Tendency. arXiv preprint arXiv:1910.12545.
Rayat, C.S., 2018. Measures of Central Tendency. In Statistical Methods in Medical
Research (pp. 33-46). Springer, Singapore.
Black, W.H. and Masten, L.B., 2020. Empirical Investigation of Alternative Measures of Central
TendencyEmpirical Investigation-Measures of Central Tendency. Journal of Forensic
Accounting Research.
Ali, Z., Bhaskar, S.B. and Sudheesh, K., 2019. Descriptive statistics: Measures of central